Линейное программирование (симплекс-метод) для лекции

1.

Модель принятия решения
Первый этап:
Формулировка задачи
управления
Второй этап:
Построение
математической модели
задачи управления
Третий этап:
Подбор метода
решения задачи.
Создание
алгоритма решения
Математическая модель – записанная в
математических символах абстракция
реальной задачи
Решение задачи – выбор программы
действий (алгоритма), приводящих к
получению наилучшего результата
МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ

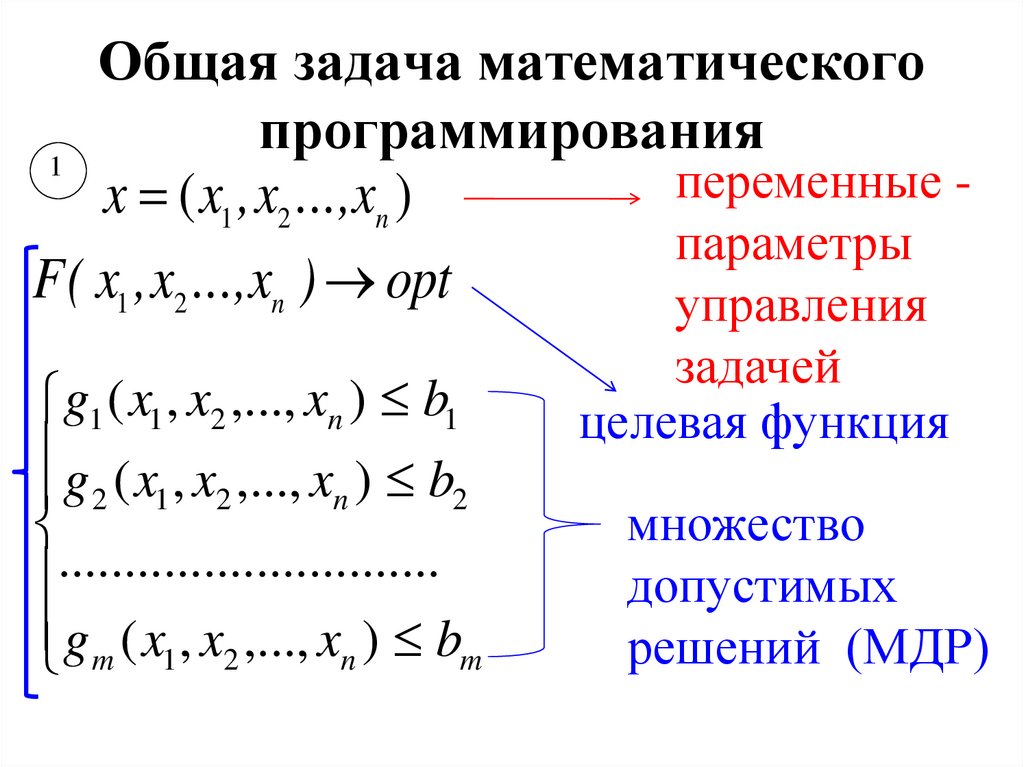
2. Общая задача математического программирования

1
переменные x ( x1 , x2 ...,xn )
параметры
F ( x1 , x2 ...,xn ) opt
управления
g1 ( x1 , x2 ,..., xn ) b1
g ( x , x ,..., x ) b
2 1 2
n
2
.............................
g m ( x1 , x2 ,..., xn ) bm
задачей
целевая функция
множество
допустимых
решений (МДР)

3.

Допустимое решение:
x ( x , x ,..., x ) МДР
i
i
1
i
2
i
n
Оптимальное решение:
x ( x , x ,..., x ) МДР
0
0
1
0
2
0
n
F ( x , x ,..., x ) opt
0
1
0
2
0
n
xi МДР
и
i
1
i
2
i
n
F ( x , x ,..., x )

4.

Задача линейного программирования
в общем виде (стандартная форма):
2
целевая функция
С
x
min
j
j
j 1
n
a x b , i 1, m
ij j
i
множество
j 1
допустимых
n
решений (МДР)

5.

Каноническая форма задачи
линейного программирования
3
n
С j x j min
j 1
n
aij x j bi (i 1, m)
j 1
x 0
( j 1, n)
j

6.

Приведение к каноническому
виду
n
C j x j min
j 1
a11 x1 .. a1n xn b1
.............................
aq1 x1 ... aqn xn bq
aq 1,1 x1 ... aq 1, n xn bq 1
..............................
a x ... a x b
rn n
r
r1 1
ar 1,1 x1 ... ar 1, n xn br 1
...............................
am1 x1 ... amn xn bm
x j 0 ( j 1, n)
(I)
(II)
(III)
n
C j x j 0 xn 1 ... 0 xn r min
j 1
n
aij x j xn i bi (i 1, q )
j 1
n
aij x j xn i bi (i q 1, r )
j 1
n
aij x j bi (i r 1, m)
j 1
x j 0 ( j 1, n r )

7. Симплекс-метод решения задачи линейного программирования

3
L C1 x1 C2 x2 Cn xn min
x x ... x
12 2
1n n
1
11 1
21 x1 22 x2 ... 2 n xn 2
.............................................
m1 x1 am 2 x2 ... mn xn m
x j 0, j 1, n
где m n, rang A m

8.

Первое базисное решение
Базисные переменные – переменные, которые
x1 ,..., xв mкотором свободные
Выразим переменные
Базисное
решение – решение,
выражаются через некоторые другие переменные.
переменные равны нулю, а базисные
: через которые
x
,...,
x
через
переменные
Свободные
переменные
–
переменные,
m
1
n
переменные равны свободным коэффициентам
выражены базисные переменные.
4
x1 b1 (a1,m 1 xm 1 ...a1 j x j ... a1n xn )
..........................................................
xi bi (ai ,m 1 xm 1 ...aij x j ... ain xn )
bi 0, i 1, m
..........................................................
xm bm (am ,m 1 xm 1 ...amj x j ... amn xn )
L 0 ( m 1 xm 1 ... j x j ... n xn )

9.

Отыскание начального
допустимого базиса
4
1...xm 1C
a1n xn )
an1 j x
...
b1C 1(xa11,m
x1
j ... min
nx
........
..........
..........
..........
..........
b
x
a
...
x
.......... a
1
1n n
11 1
xi
bi (ai ,m 1 xm 1 ...aij x j ... ain xn )
.........................
.......... ..........
.......... .......... .......... .......... ........
a
b
x
a
...
n
mn
1
xm bmm 1 x
(am,m 1 xm 1 ...amj x j ...m amn xn )
L
0x j ( m 01 xm( j1 ...1 , jnx)j ... n xn ) min
bi 0, (i 1, m)
3

10.

Постановка V-задачи
5
V V1 ... Vm min
V1 a11 x1 ... a1n xn b1
...................................
V a x ... a x b
m1 1
mn n
m
m
x j 0 ( j 1, n), Vi 0 (i 1, m)

11.

Допустимый начальный базис
V-задачи
V min
V b (a x ... a x )
1
1
11 1
1n n
.......... .......... .......... .........
Vm bm (a m1 x1 ... a mn xn )
bi 0, (i 1, m)

12.

Варианты решения V-задачи
исходная задача имеет хотя бы одно
Vmin=0 - допустимое решение
система ограничений исходной
Vmin>0 - задачи несовместна (решений нет)
V V1 ... Vm min
V1 a11 x1 ... a1n xn b1
...................................
V a x ... a x b
m1 1
mn n
m
m
x j 0 ( j 1, n), Vi 0 (i 1, m)