Similar presentations:
Комплексные числа
1.
2.
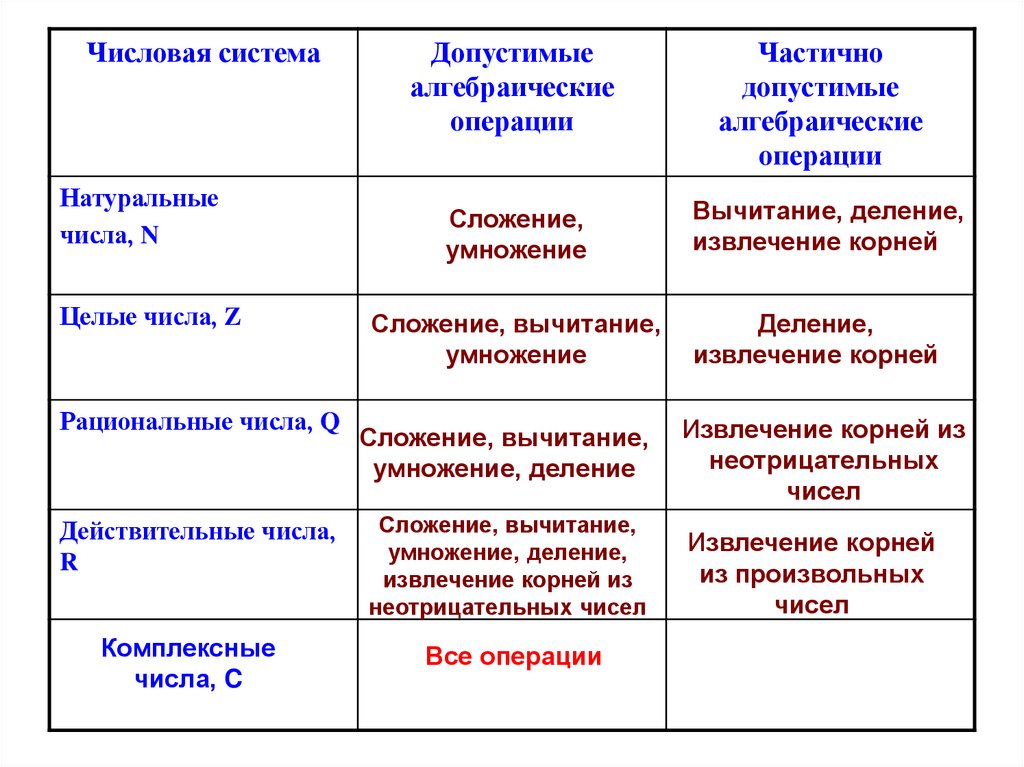
Числовая системаДопустимые
алгебраические
операции
Частично
допустимые
алгебраические
операции
Сложение,
умножение
Вычитание, деление,
извлечение корней
Сложение, вычитание,
умножение
Деление,
извлечение корней
Сложение, вычитание,
умножение, деление
Извлечение корней из
неотрицательных
чисел
Действительные числа,
R
Сложение, вычитание,
умножение, деление,
извлечение корней из
неотрицательных чисел
Извлечение корней
из произвольных
чисел
Комплексные
числа, C
Все операции
Натуральные
числа, N
Целые числа, Z
Рациональные числа, Q
3.
4.
Минимальные условия, которым должны удовлетворятькомплексные числа:
Существует квадратный корень из i , т.е. существует
комплексное число, квадрат которого равен -1 .
1)
Множество
комплексных
действительные числа.
2)
чисел
содержит
все
Операции сложения, вычитания, умножения и деления
комплексных чисел удовлетворяют обычным законам
арифметических
действий
(сочетательному,
переместительному, распределительному).
3)
Выполнение этих минимальных условий позволяет определить
все множество С комплексных чисел.
5. Мнимые числа
i2 = -1, i – мнимая единицаi, 2i, -0,3i — чисто мнимые числа
Арифметические операции над чисто мнимыми числами
выполняются в соответствии с условием С3.
3i 13i 3 13 i 16i
3i 13i 3 13 i i 39i 2 39
i
7
i
2
i i
3
В общем виде правила арифметических операций с чисто
мнимыми числами таковы:
ai bi a b i; ai bi a b i;
ai bi abi ab
a bi ab i;
2
где a и b — действительные числа.
6. Степени мнимой единицы
По определению первой степенью числа i является самочисло i, а второй степенью – число -1:
i1 = i, i2 = -1
Более высокие степени числа i находятся следующим образом:
i4 = i3 ∙ i = -∙i2= 1;
i5 = i4 ∙ i = i;
i6 = i5 ∙ i = i2= - 1 и т.д.
Очевидно, что при любом натуральном n
i4n = 1;
i4n +2 = - 1
i4n+1 = i;
i4n+3 = - i.
Вычисли самостоятельно: 1) i66; i143; i216; i137.
2) (i36 + i17)i23.
7. Комплексные числа
Определение 1. Комплексным числом называют суммудействительного числа и чисто мнимого числа.
Определение 2. Два комплексных числа
называют равными, если равны их
действительные части и равны их
мнимые части:
8. Свойства сопряженных чисел
1. Сумма и произведение двух сопряженных чисел есть числодействительное.
z z ( a bi ) ( a bi ) 2a
z z ( a bi )( a bi ) a 2 (bi ) 2 a 2 b 2
2. Число, сопряженное сумме двух комплексных чисел, равно сумме
сопряженных данным числам.
z1 z2 z1 z2
3. Число, сопряженное разности двух комплексных чисел, равно
разности сопряженных данным числам.
z1 z2 z1 z2
4. Число, сопряженное произведению двух комплексных чисел, равно
произведению сопряженных данным числам.
z1 z2 z1 z2
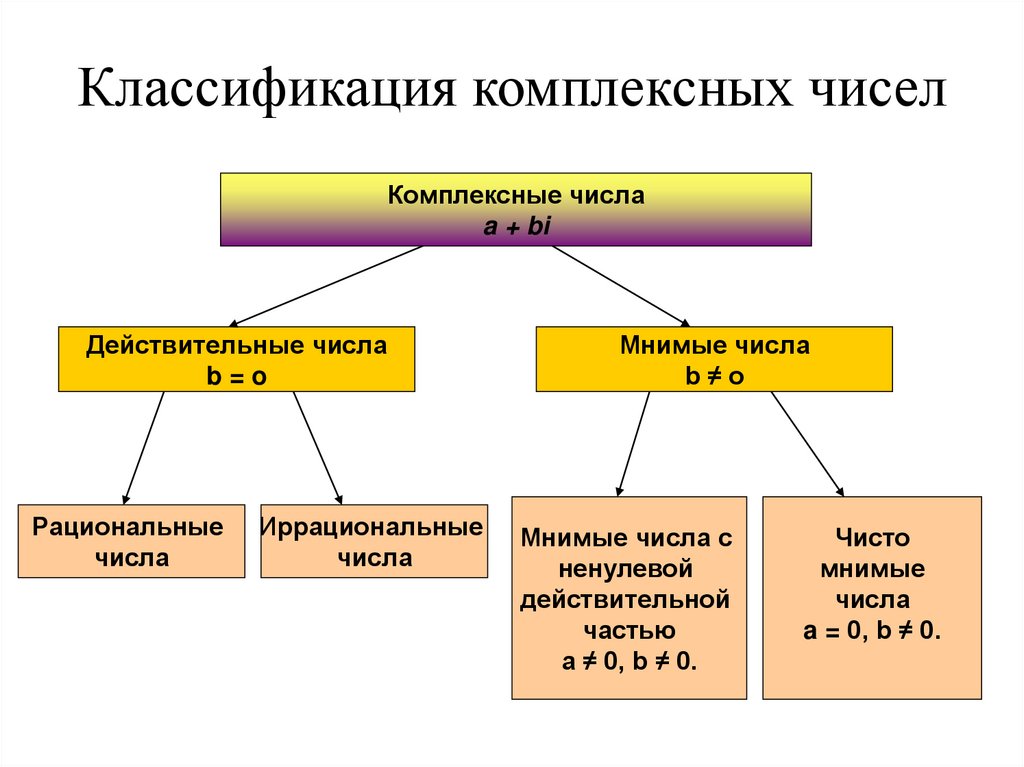
9. Классификация комплексных чисел
Комплексные числаa + bi
Действительные числа
b=o
Рациональные
числа
Иррациональные
числа
Мнимые числа
b≠o
Мнимые числа с
ненулевой
действительной
частью
a ≠ 0, b ≠ 0.
Чисто
мнимые
числа
a = 0, b ≠ 0.
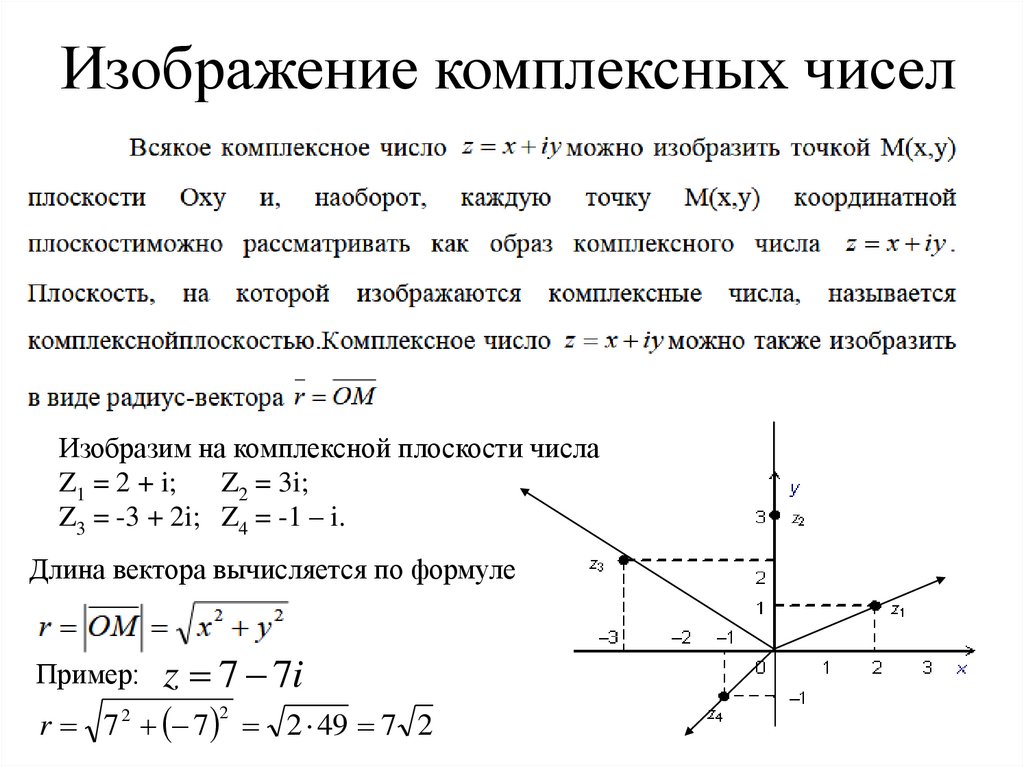
10. Изображение комплексных чисел
Изобразим на комплексной плоскости числаZ1 = 2 + i;
Z2 = 3i;
Z3 = -3 + 2i; Z4 = -1 – i.
Длина вектора вычисляется по формуле
z 7 7i
2
r 7 2 7 2 49 7 2
Пример:
11. Действия над комплексными числами в алгебраической форме
;Действия над комплексными числами в
алгебраической форме
Сложение (а + bi) + (c + di) = (а + с) + (b + d)i
Вычитание (а + bi) - (c + di) = (а - с) + (b - d)i
Произведение (а + bi)·(с + di) = (ac - bd) + (ad + bc)i
a bi (a bi)(c di) ac bd bc ad
2
Деление
2 2
2 i
c di (c di)(c di) c d
c d
Выполнить сложение, вычитание, умножение и деление комплексных чисел
в алгебраической форме. z1 2 4i; z 2 6 8i
Решение.
z1 z 2 2 6 4 8 i 8 12i
z1 z 2 2 6 4 8 i 4 4i
z1 z 2 2 6 4 8 2 8 4 6 i 20 40i
z1 2 4i 6 8i 12 32 16 24 i 44 8i
0,44 0,08i
2
2
z 2 6 8i 6 8i
100
6 8
12. Тригонометрическая форма комплексного числа
z r cos i sinгде φ – аргумент комплексного числа, r =
комплексного числа,
a 2 b2
a b
a2 b2
cos
a
2
2
и sin
b
Задание: Вычислить модуль и аргумент комплексного числа
Записать комплексное число в тригонометрической форме.
2
Решение.
r 7 2 7 2 49 7 2
7
3
1,
7
4
3
3
z 7 7i 7 2 cos
i sin
4
4
tg
- модуль
z 7 7i
13. Умножение и деление комплексных чисел, заданных в тригонометрической форме
z1 0, z2 0 и z1 r1 cos 1 i sin 1 , z2 r2 cos 2 i sin 2 ,то: а) z1 z2 r1r2 cos 1 2 i sin 1 2
Если
б)
z1 r1
cos 1 2 i sin 1 2
z2 r2
Пусть z — любое отличное от нуля комплексное число, п — любое целое
число.
n
n
r n cosn i sin n .
Тогда z r cos i sin
Задание: Вычислить модуль и аргумент комплексного числа
Записать комплексное число в тригонометрической форме.
Решение. r 7 2 7 2 2 49 7 2
7
3
tg
1,
7
4
z 7 7i
14. Решение задач
15.
16.
17. Решение квадратных уравнений
Замечание: если дискриминант квадратного уравнения отрицателен, токвадратное уравнение имеет два сопряженных комплексных корня.
18.
Задания для практического занятияЗадание 1. Изобразить комплексное число в комплексной плоскости.
Задание 2. Выполнить сложение, вычитание, умножение и деление
комплексных чисел в алгебраической форме.
Задание 3. Запишите комплексное число в тригонометрической форме.
Задание 4. Решить квадратные уравнения:
а) x2 – 4x + 13 = 0
б) 2,5x2 + x + 1 = 0
Задание 1
Задание 2
Задание 3
А)
Z= -6+8i
Z=3+3i
Б)
Z=9-3i
Z1=4-2i
Z2=8+6i
Z1=3-7i
Z2= -3+4i












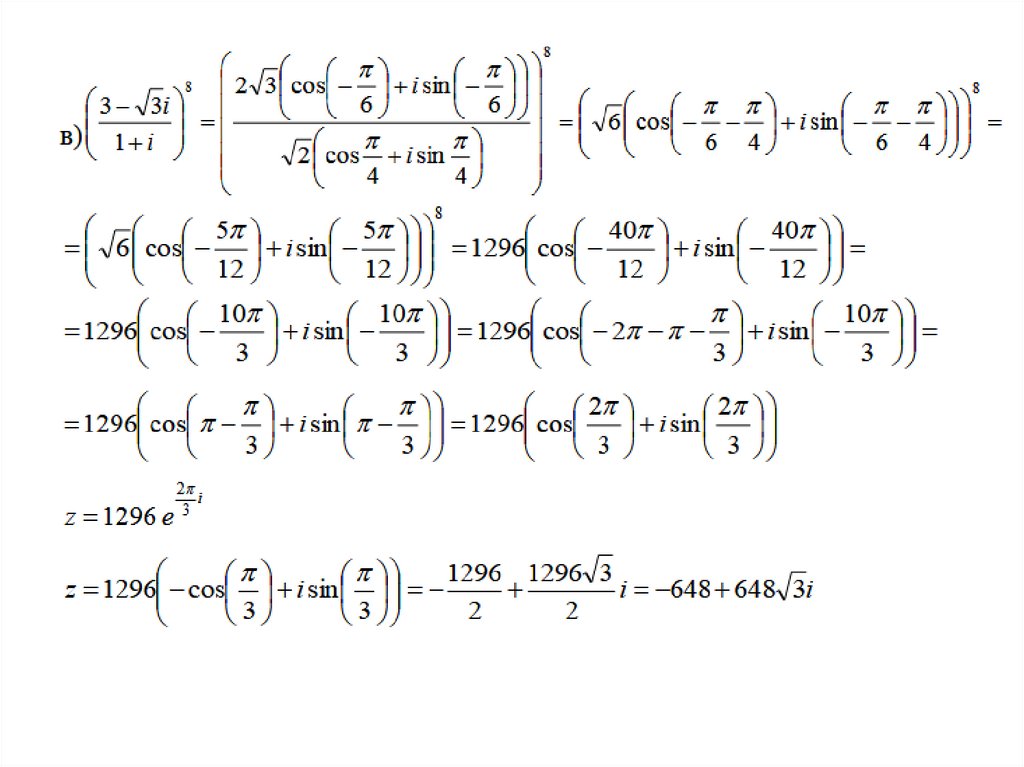


 mathematics
mathematics








