8olaymWfpudZA9BhE9c8dMzPEoOJ0cQ2u18PzxgW

1.

5- маъруза
Электр схемаларни
Кирхгоф қонунлари
асосида ҳисоблаш

2. Режа

1. Кирхгоф қонунлари (1) ва (2).
2. Кирхгоф қонунлари асосида электр занжирини
ҳисоблаш.
3. Манбалар.
4. Мустақил ва номустақил манбалар.
5. Элементларни кетма-кет ва параллел улаш.

3. Кирхгоф қонунлари

XIX
асрнинг
немис
физиги Густав Роберт
Ки́рхгоф 1824, Кёнигс
берг
(Шарқий
Пруссия)
—
1887, Берлин).
1935
йил
Халқаро
астроном
иттифоқи
унинг номи билан
Ойнинг
кўринарли
қисмидаги
кратерга
ном берган.

4. Кирхгоф қонунлари

1 қонун
Тугунга кираётган токларнинг суммаси
тугундан чиқаётган токлар суммасига тенг.
Тугундаги токларнинг алгебраик суммаси
нолга тенг.
Бу тугунларда заряд йиғилмаслигини
англатади.

5. Кирхгоф қонунлари (1)

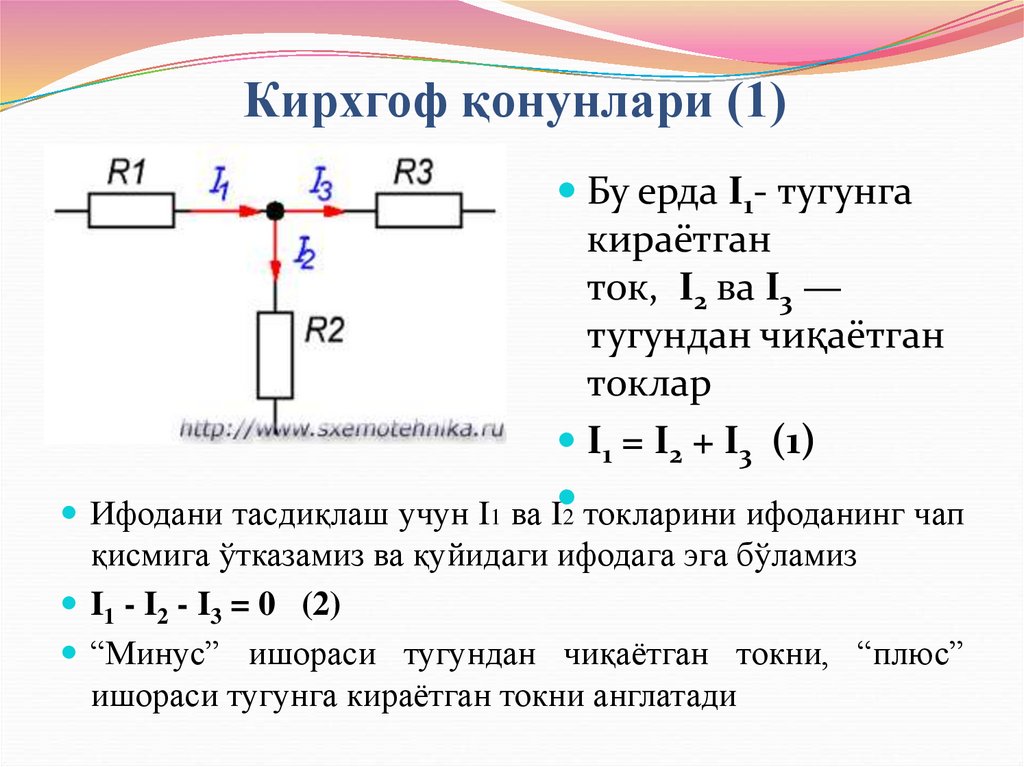
Бу ерда I1- тугунга
кираётган
ток, I2 ва I3 —
тугундан чиқаётган
токлар
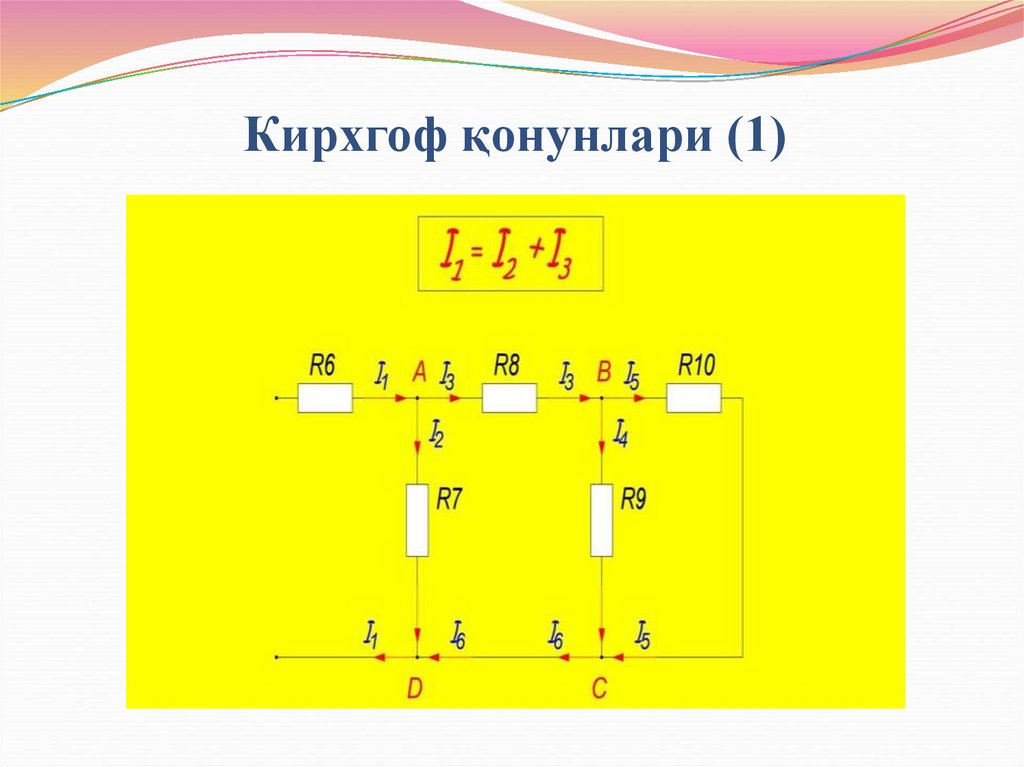
I1 = I2 + I3 (1)
Ифодани тасдиқлаш учун I1 ва I 2 токларини ифоданинг чап
қисмига ўтказамиз ва қуйидаги ифодага эга бўламиз
I1 - I2 - I3 = 0 (2)
“Минус” ишораси тугундан чиқаётган токни, “плюс”
ишораси тугунга кираётган токни англатади

6. Кирхгоф қонунлари (1)

7. Кирхгоф қонунлари (1)

8. Кирхгоф қонунлари

2 қонун
Занжир
контури
тугунларидаги
кучланишларнинг алгебраик суммаси нолга тенг.
Берк контурдаги ЭЮК нинг алгебраик суммаси
шу
контур
резистив
элементларидаги
кучланишларнинг (тушиш) алгебраик суммасига
тенг.
Бу ерда алгебраик сумма ибораси, элементларда
ЭЮК ва кучланишлар тушиши қийматлари “+”
ёки “-” ишораси билан бўлиши мумкинлигини
англатади.

9. Кирхгоф қонунлари (2)

Ишораларни қуйидаги алгоритм бўйича аниқлаш мумкин:
Контурни айланиб ўтиш йўналишини танлаймиз (2 та
вариант, соат стрелкаси бўйича ва унга қарши йўналишда)
Исталган тартибда занжир элементлари орқали токнинг
йўналишини танлаймиз
ЭЮК ва элементларга тушаётган кучланишларнинг
ишорасини қўямиз
Контурда ток ҳосил қилувчи ЭЮК (элементга тушувчи
кучланиш) нинг йўналиши контурни айланиб ўтиш
йўналиши билан мос келса “+”, акс ҳолда “-” ишораси
билан ёзилади.

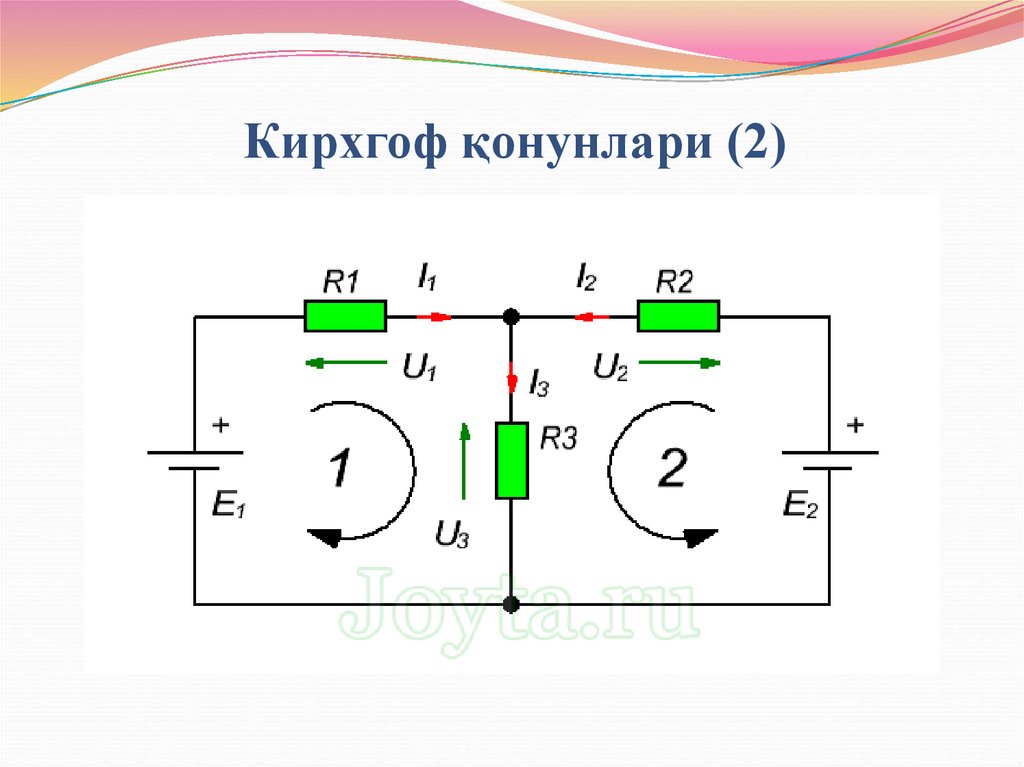
10. Кирхгоф қонунлари (2)

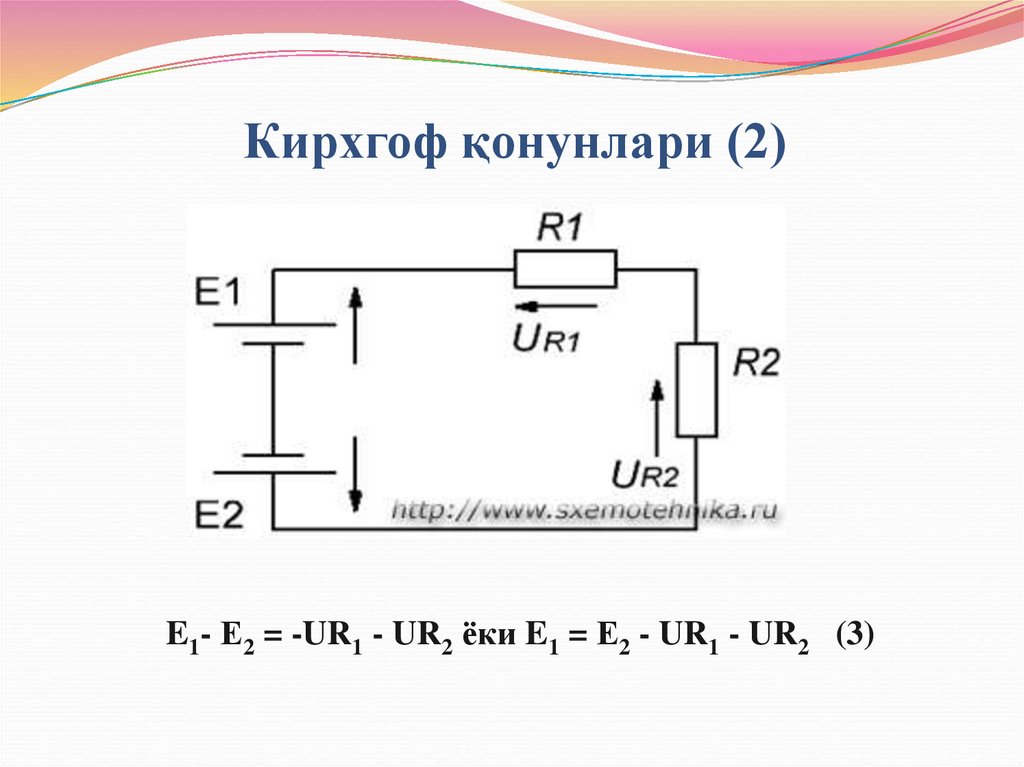
E1- Е2 = -UR1 - UR2 ёки E1 = Е2 - UR1 - UR2 (3)

11. Кирхгоф қонунлари (2)

12. Кирхгоф қонунлари (2)

13. Кирхгоф қонунлари асосида ЭЗ ҳисоблаш

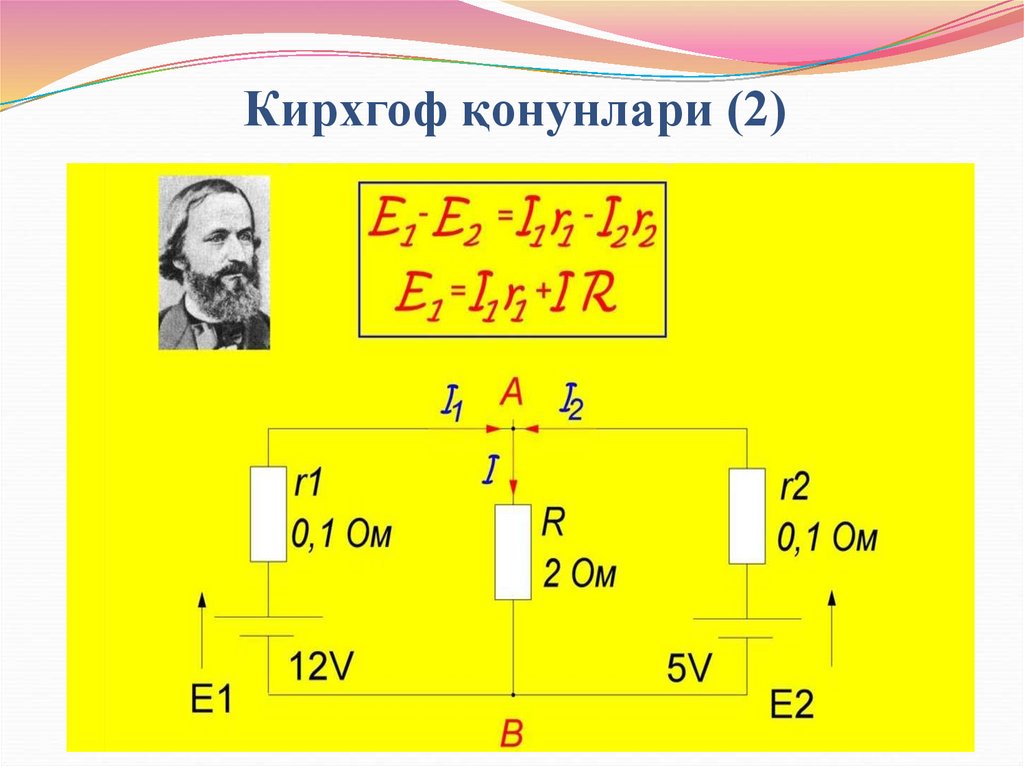
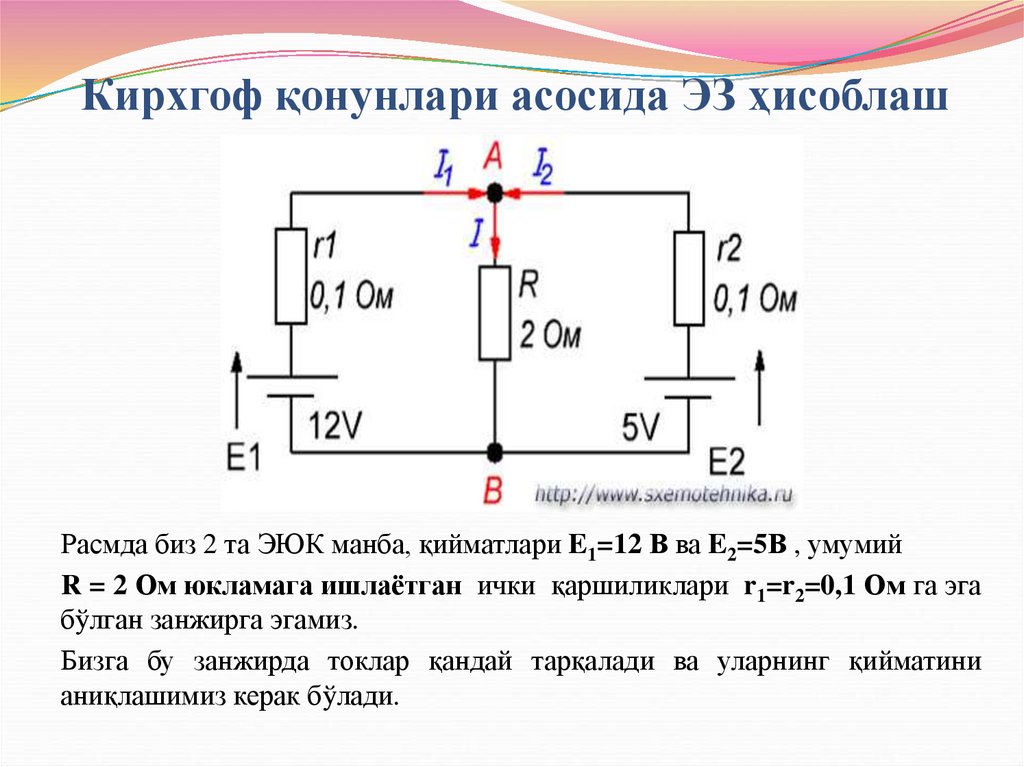
Расмда биз 2 та ЭЮК манба, қийматлари E1=12 В ва E2=5В , умумий
R = 2 Ом юкламага ишлаётган ички қаршиликлари r1=r2=0,1 Ом га эга
бўлган занжирга эгамиз.
Бизга бу занжирда токлар қандай тарқалади ва уларнинг қийматини
аниқлашимиз керак бўлади.

14. Кирхгоф қонунлари асосида ЭЗ ҳисоблаш

Кирхгофнинг 1 қонунига асосан А тугуни учун ток
қуйидагича ифодаланади: I = I1 + I2,
Кирхгофнинг 2 қонунини қўллаган ҳолда, соат стрелкаси
бўйича контурни айланиб ўтиш йўнлалишини танлаб, ташқи
ва ички (чап) контур учун яна 2 та ифодани ёзамиз:
Ташқи контур учун:
E1-E2 = Ur1 – Ur2 ёки E1-E2 = I1*r1 – I2*r2
Ички (чап) контур учун:
E1 = Ur1 + UR ёки E1 = I1*r1 + I*R
Шундай қилиб биз 3 та номаълум тенгламага эга бўлдик:
I = I1 + I2; E1-E2 = I1*r1 – I2*r2; E1 = I1*r1 + I*R.

15. Кирхгоф қонунлари асосида ЭЗ ҳисоблаш

Энди биз бунга бизга маълум бўлган қаршилик ва кучланиш қийматларини
қўямиз: I = I1 + I2; 7 = 0,1I1 – 0,1I2; 12 = 0,1I1 +2I.
Биринчи ва иккинчи тенгламадан I2 токни ифодалаймиз:
I2=I - I1; I2 = I1 – 70; 12 = 0,1I1 + 2I.
Кейинги босқичда биринчи ва иккинчи тенгламаларни тенглаштириб иккита
тенламалар тизимига эга бўламиз: I - I1= I1 – 70; 12 = 0,1I1 + 2I.
Биринчи тенгламадан ток I нинг қийматини ифодалаймиз: I = 2I1– 70;
Унинг қийматини иккинчи тенгламага қўямиз 12 = 0,1I1 + 2(2I1 – 70).
Олинган тенгламани ечамиз:
12 = 0,1I1 + 4I1 – 140. 12 + 140= 4,1I1 I1=152/4,1 I1=37,073 (А)
Энди I = 2I1– 70 ифодага I1=37,073 (А) қийматини қўямиз ва қуйидагига
эга бўламиз: I = 2*37,073 – 70 = 4,146 А
Кирхгофнинг 1 қонунига асосан ток I2=I - I1 I2=4,146 - 37,073 = -32,927
I2 токи учун “минус” ишораси бу биз токнинг йўналишини нотўғри
олганимизни англатади, яъни бизнинг ҳолатда I2 токи А тугунидан
чиқаяпти.

16. Кирхгоф қонунлари асосида ЭЗ ҳисоблаш

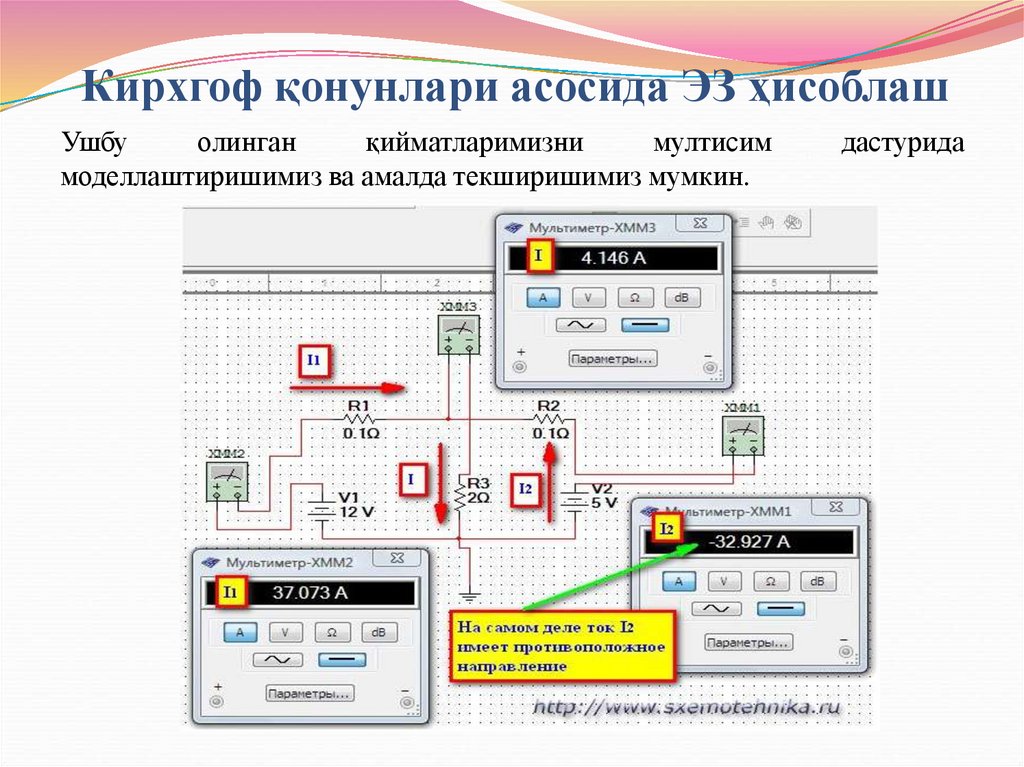
Ушбу
олинган
қийматларимизни
мултисим
моделлаштиришимиз ва амалда текширишимиз мумкин.
дастурида

17. Кирхгоф қонунлари   Электр занжирларини ҳисоблаганда Кирхгофнинг икки қонуни, Ом қонуни, алмаштириш теоремаси қўлланилади.

Кирхгоф қонунлари
Электр занжирларини ҳисоблаганда Кирхгофнинг икки қонуни, Ом
қонуни, алмаштириш теоремаси қўлланилади. Уларни мужассамланган
параметрли занжирларни ҳисоблашда кўриб чиқамиз.
Кирхгофнинг биринчи қонуни чет тиллардаги адабиётларда ҳар хил
номларда учрайди, шулардан иккинчи номи Кирхгофнинг токлар
қонуни, учинчиси Кирхгофнинг тугунлар учун қонуни – электр занжирининг тугунлари учун қўлланилади ва электр токининг узлуксизлиги принципига асосланади. Кирхгофнинг токлар қонуни-электр (заряд)
миқдори сақланиш қонунидан келиб чиқувчи натижадир; унданда кўра
аҳамиятлироқ қилиб айтганда - бу энергия сақланиш қонунининг электр
занжирлари «тилидаги» ифодасидир: занжирнинг бир тугунига шохобчалардан келувчи барча токлар йиғиндиси, ушбу тугундан чиқиб
кетаётган барча токлар йиғиндисига тенг.

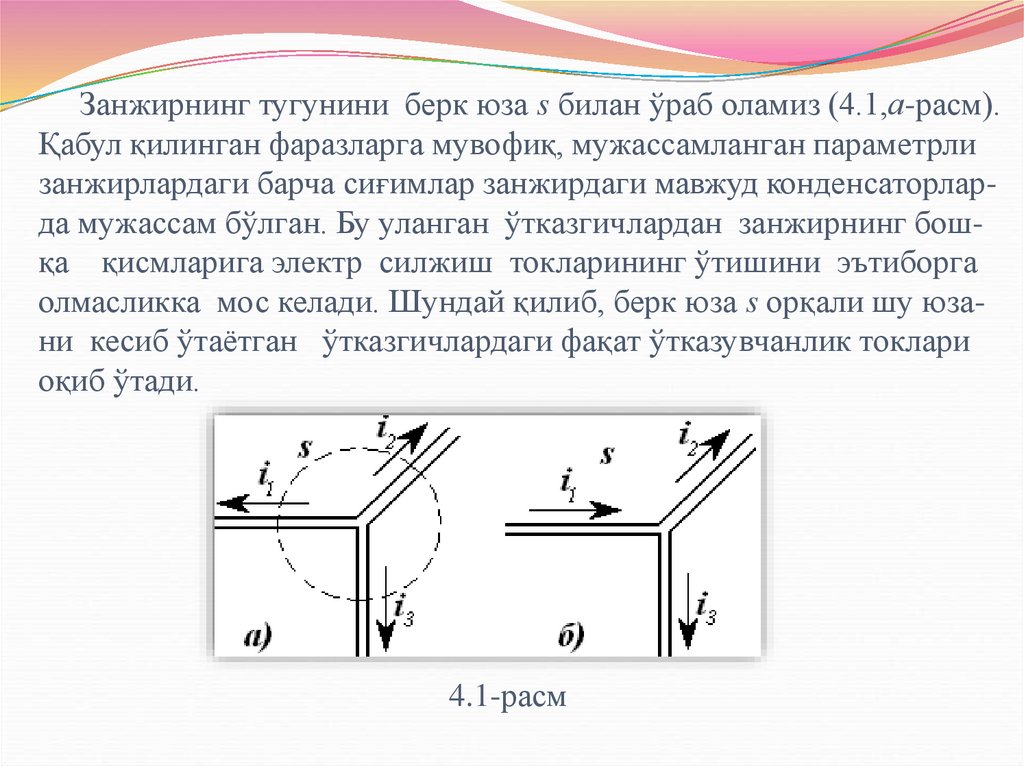
18. Занжирнинг тугунини берк юза s билан ўраб оламиз (4.1,а-расм). Қабул қилинган фаразларга мувофиқ, мужассамланган параметрли

занжирлардаги барча сиғимлар занжирдаги мавжуд конденсаторларда мужассам бўлган. Бу уланган ўтказгичлардан занжирнинг бошқа қисмларига электр силжиш токларининг ўтишини эътиборга
олмасликка мос келади. Шундай қилиб, берк юза s орқали шу юзани кесиб ўтаётган ўтказгичлардаги фақат ўтказувчанлик токлари
оқиб ўтади.
4.1-расм

19. Токнинг узлуксизлиги принципи асосида, бу ҳолат учун қуйидаги ифодага эга бўламиз: Jds = i1 + i2 + i3 = 0. Занжирнинг тугунига

уланган ихтиёрий п шохобча учун
n
i 0,
(4.1)
яъни, электр занжирининг тугунидаги токлар алгебраик йиғиндиси
нолга тенг, мана шу Кирхгоф биринчи қонунининг таърифидир.
Кирхгоф биринчи қонунининг ҳар хил номлари ичида, унинг моҳиятини аниқроқ ифодалайдигани - Кирхгофнинг токлар қонуни номидир.
Токларнинг мусбат йўналиши тугундан бошланса,(4.1) тенгламанинг
чап томонидаги токларнинг ҳарфли белгиларига «плюс» ишорасини,
мусбат йўналиши тугун томон йўналган бўлса, токларнинг ҳарфли
белгиларига «минус» ишорасини қўйилади. 4.1,а-расмдаги ҳолат учун
тенгламанинг барча токлари учун «плюс» ишора, 4.1,б-расмдаги ҳолат
учун эса қуйидагича ёзиш керак:
-i1 + i2 + i3 = 0.
(4.1,а)
k 1
k

20. Кирхгофнинг иккинчи қонуни, ёки бошқа номлардаги Кирхгоф-нинг контурлар учун қонуни, ёки Кирхгофнинг кучланишлар қонуни электр

Кирхгофнинг иккинчи қонуни, ёки бошқа номлардаги Кирхгофнинг контурлар учун қонуни, ёки Кирхгофнинг кучланишлар
қонуни электр занжирларининг берк контурлари учун қўлланилади
E dl = Eинд dl + Eташқ dl .
(4.2)
Eташқdl қиймат контурга таъсир этаётган ташқи манбалар ЭЮК
ларининг Σеташқ йиғиндисидир. Тенгламанинг Eинд dl ташкил
этувчиси таркибига контурдаги барча индуктивланаётган ЭЮКлар–
ҳам электромагнит индукцияси, ҳам ўзиндукция,ҳам ўзаро индкция
асосидаги ЭЮКлар киради. Агар (4.2)нинг биринчи ташкил этувчисига энергия манбаси сифатида фақат генераторлардаги ЭЮКларининг йиғиндиси Σеинд ни киритсак, у ҳолда ғалтаклардаги индуктивланаётган ўзиндукция ва ўзаро индукция ЭЮКларини тенгламанинг чап томонига ўтказилиши ва E dl нинг таркибига киритилиб,
ғалтак клеммаларидаги кучланишлар пасаюви сифатида эътиборга
олиниши шарт.

21. Масалан, ғалтак учун тенгламанинг чап томонида иL = +L di / dt пайдо бўлади. Чап томондаги E dl таркибига, яна контурга

кирувчи реостатдаги кучланишлар пасаюви ri ҳам, конденсатордаги uC =
q/C кучланишлар пасаюви ҳам киради. Контурнинг барча п шохобчаларидаги энергия манбалари ЭЮКларининг йиғиндисини қуйидагича белгилаймиз
k n
л
ундан
k n
e e
k .таш
л
k n
k 1
k
k 1
u e
k 1
k
k 1
ek .инд
k 1
k
(4.3)
Шундай қилиб, Кирхгофнинг иккинчи қонуни қуйидагича талқин
этилади: электр занжирининг ихтиёрий берк контурдаги барча
шохобчалари кучланишлар пасаювининг йиғиндиси шу контурга
таъсир этаётган энергия манбалари ЭЮКларининг йиғиндсига
тенг.

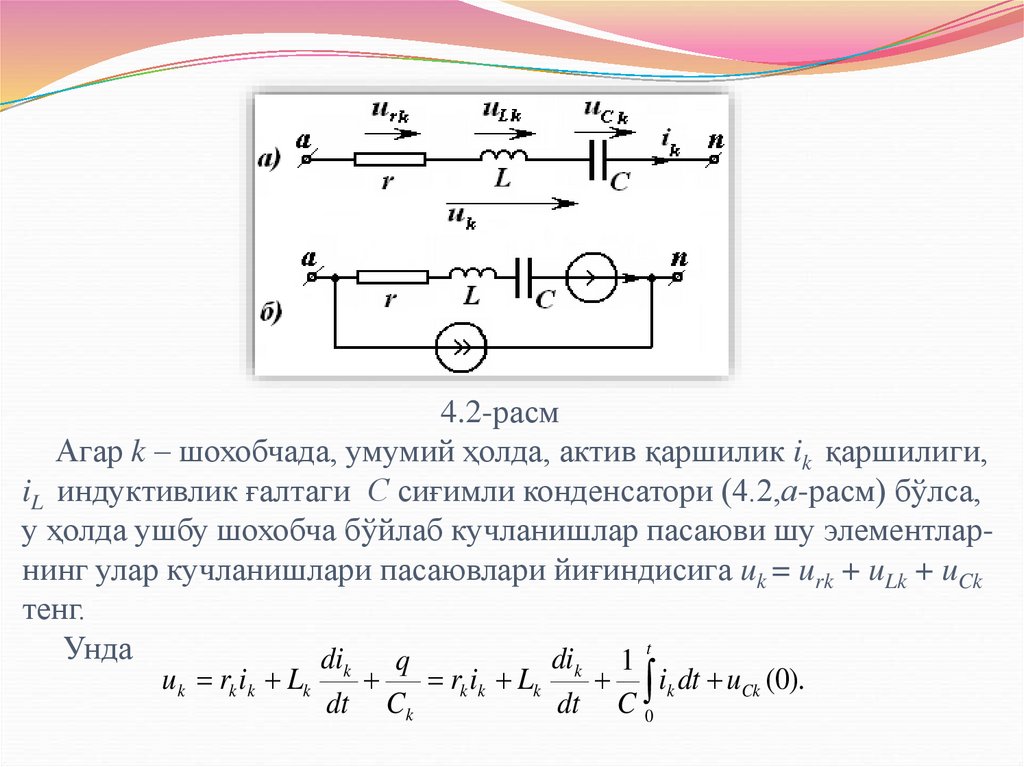
22. 4.2-расм Агар k – шохобчада, умумий ҳолда, актив қаршилик ik қаршилиги, iL индуктивлик ғалтаги С сиғимли конденсатори

(4.2,а-расм) бўлса,
у ҳолда ушбу шохобча бўйлаб кучланишлар пасаюви шу элементларнинг улар кучланишлари пасаювлари йиғиндисига uk = urk + uLk + uCk
тенг.
t
Унда
di
di
q
1
u k rk ik Lk
k
dt
Ck
rk ik Lk
k
dt
i dt u (0).
C
k
0
Ck

23. Мужассамланган параметрли электр занжирларида Кирхгоф-нинг иккинчи қонуни электр занжирини қуршаб олган фазо орқали бир

Мужассамланган параметрли электр занжирларида Кирхгофнинг иккинчи қонуни электр занжирини қуршаб олган фазо орқали
бир тугундан иккинчи тугунга ўтадиган контур учун ҳам ёзилиши
мумкин. Мужассамланган параметрли электр занжирлари назариясини қуришда қабул қилинган илмий абстракциялар асосида шуни
эътиборга олишимиз зарурки, бу занжирни қуршаб олган фазода
магнит ва ташқи майдонлар бўлмаслиги зарур, демак, еташқ ва еинд
ЭЮКлар нолга тенг бўлиши шарт. Контурни бундай айланиш йўналишини танлаганда қуйидагини ёзиш мумкин
E dl = umn 0,
(4.4)
бунда - m ва n тугунлар орасидаги кучланишлар.
Шунга эътибор берайликки, мужассамланган параметрли занжирнинг ташқи фазосида ҳам электр майдони мавжуд деб ҳисобланса, интеграл айрим маънога эга бўлади. Аммо бундай майдон
энергияси ва силжиш токлари жуда кичик ва эътиборга олмаса ҳам
бўлади, деб ҳисобланади.

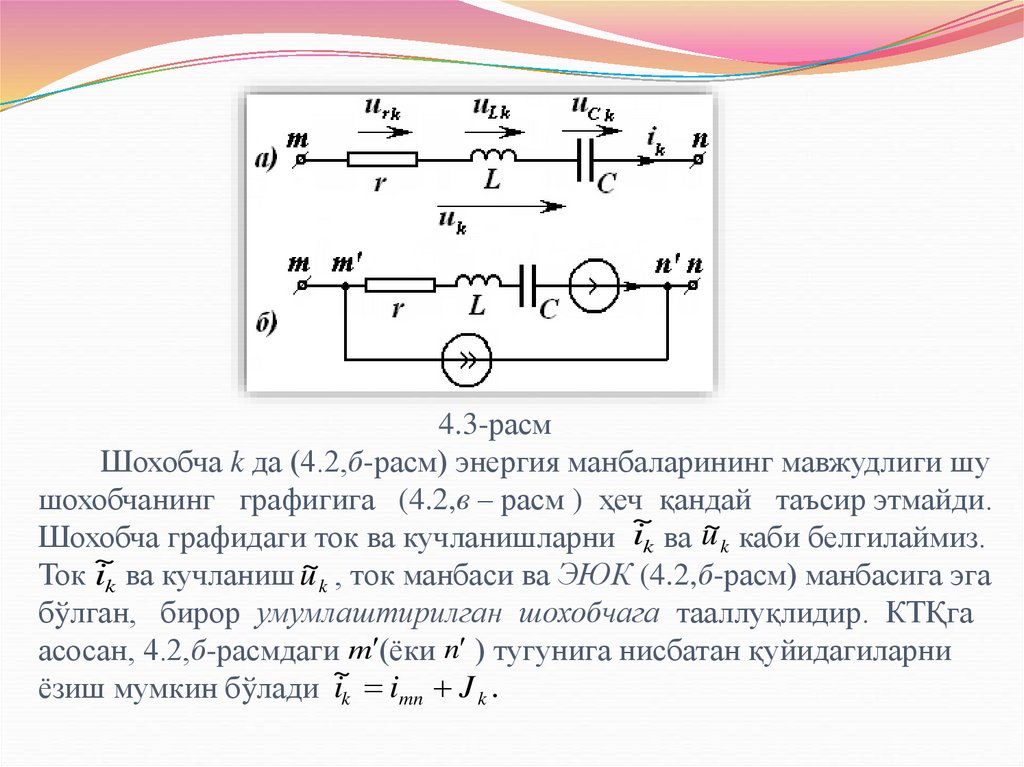
24. 4.3-расм Шохобча k да (4.2,б-расм) энергия манбаларининг мавжудлиги шу шохобчанинг графигига (4.2,в – расм ) ҳеч қандай таъсир

этмайди.
~
Шохобча графидаги ток ва кучланишларни ik ва u~k каби белгилаймиз.
ik ва кучланиш u~k , ток манбаси ва ЭЮК (4.2,б-расм) манбасига эга
Ток ~
бўлган, бирор умумлаштирилган шохобчага тааллуқлидир. КТҚга
асосан, 4.2,б-расмдаги m (ёки n ) тугунига нисбатан қуйидагиларни
ik imn J k .
ёзиш мумкин бўлади ~

25. Кирхгофнинг иккинчи қонунига мувофиқ, k шохобча ўтказгич-ларидан m тугундан n тугунга ўтаётган ва ташқи фазодан – n тугун-дан m

Кирхгофнинг иккинчи қонунига мувофиқ, k шохобча ўтказгичларидан m тугундан n тугунга ўтаётган ва ташқи фазодан – n тугундан m тугунга ўтаётган контур учун қуйидагини ҳосил қиламиз
t
ik
d
~
u mn u k u k ek rk ik ( Lk ik ) dt uCk (0) ek
dt
C
0 k
Кейинги ифода берилган схемада мавжуд бўлган ва схема графида
шохобчалар токлари ва кучланишлари, ток ва ЭЮК манбалари
кесмалар билан тасвирланган бўлса, графнинг умумлаштирилган
шохобчаларидаги ток ва кучланишларни боғлайди.
Кирхгоф қонунлари бўйича схема графи учун тенгламалар ёзилганда шуни кўзда тутамизки, бу тенгламалар таркибига схеманинг
умумлаштирилган шохобчаларидаги ток ва кучланишлар киради.
Демак, схема графи учун қуйидагини ёзиш мумкин:
p
p
~i 0 ва u~ 0
k 1
k
k 1
k
p
p
ёки u~k ek
k 1
k 1
(4.5)

26. Кирхгоф иккинчи қонунининг ҳар хил номлари ичида, унинг моҳиятини аниқроқ ифодалайдигани – Кирхгофнинг кучланишлар қонуни (ККҚ)

номидир. Келгусида бу қонунни мана шу номда
ишлатамиз.
Ушбу маърузада умумий ҳол учун таркибида реактив элементлари С сиғим ва L индуктивлик ҳамда R қаршилиги бўлган занжирларнинг барқарорлик жараёнларини кўрдик. Ўзгармас ток занжирларида d/dt=0 бўлганлиги учун ва, демак, шохобчага конденсатор
уланиши – шу шохобчанинг узилишини i=Cduc/dt=0 англатиши,
индуктивликнинг мавжудлиги эса ундаги кучланиш U =Ldi/dt= 0
сезиларсиз деб ҳисобланганлиги учун: КТҚ 4.1-расмдаги схемада
қуйидагича ёзиш керак:
-I1 + I2 + I3 = 0.
ККҚ эса (4.3) ўрнига қуйидагича ёзиш керак:
k n
ë
. U E
k 1
k
k 1
k
(4.5,а)

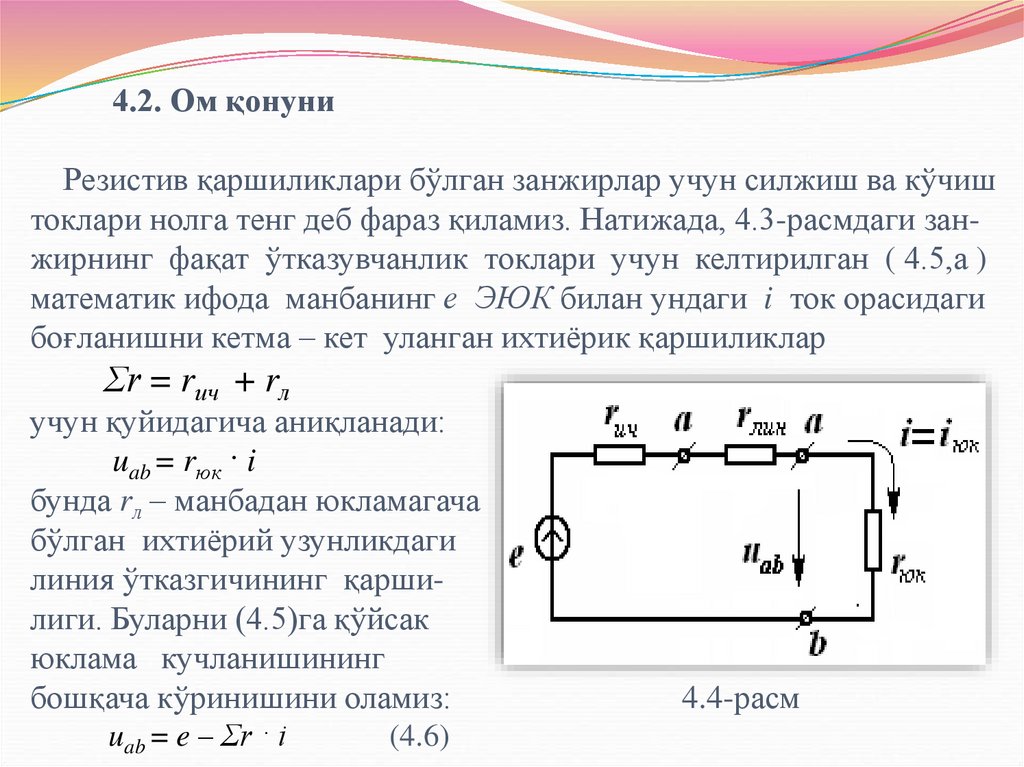
27. 4.2. Ом қонуни Резистив қаршиликлари бўлган занжирлар учун силжиш ва кўчиш токлари нолга тенг деб фараз қиламиз. Натижада,

4.3-расмдаги занжирнинг фақат ўтказувчанлик токлари учун келтирилган ( 4.5,а )
математик ифода манбанинг е ЭЮК билан ундаги i ток орасидаги
боғланишни кетма – кет уланган ихтиёрик қаршиликлар
Σr = rич + rл
учун қуйидагича аниқланади:
uab = rюк · i
бунда rл – манбадан юкламагача
бўлган ихтиёрий узунликдаги
линия ўтказгичининг қаршилиги. Буларни (4.5)га қўйсак
юклама кучланишининг
бошқача кўринишини оламиз:
uab = e – Σr · i
(4.6)
4.4-расм

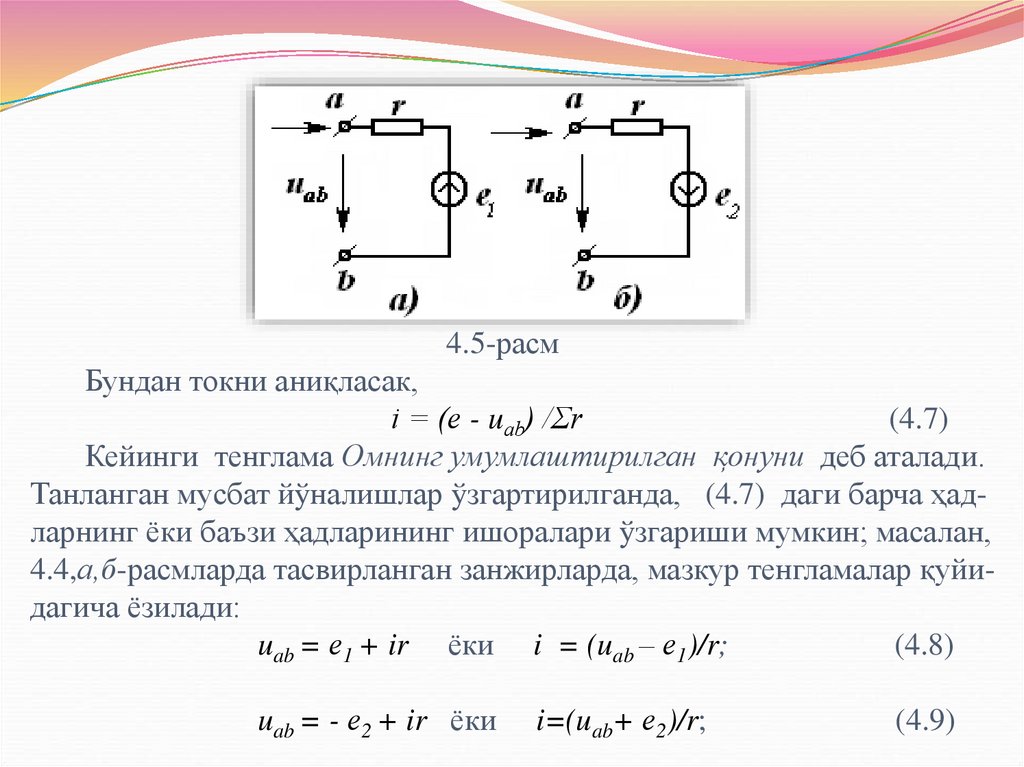
28. 4.5-расм Бундан токни аниқласак, i = (е - uаb) /Σr (4.7) Кейинги тенглама Омнинг умумлаштирилган қонуни деб аталади. Танланган

мусбат йўналишлар ўзгартирилганда, (4.7) даги барча ҳадларнинг ёки баъзи ҳадларининг ишоралари ўзгариши мумкин; масалан,
4.4,а,б-расмларда тасвирланган занжирларда, мазкур тенгламалар қуйидагича ёзилади:
uab = е1 + ir ёки i = (uab – е1)/r;
(4.8)
uab = - е2 + ir ёки
i=(uab+ е2)/r;
(4.9)

29. Кучланиш uab ни a ва b нуқталари орасидаги потенциаллар фарқи эканлигини эътиборга олинса, яъни уни φa ва φb орқали

ифодаласак, унда умумлаштирилган Ом қонуни бошқа кўриниш, масалан
(4.9) учун қуйидаги кўриниш олади:
i=( φa - φb + е2)/r.
Электр занжири элементидаги ток ва кучланиш орасидаги боғланиш
uab = r · i
занжирнинг бир қисми учун Ом қонуни дейилади.
Бир контурли занжир учун Ом қонуни
i=Σе/Σ r,
ёки Σr·i=Σе
(4.9,а)
бунда Σе – контурдаги ЭЮКлар йиғиндиси; Σr – контурдаги
қаршиликлар йиғиндиси.
Масалан, 4.5-расмдаги ташқи контур учун уни соат мили йўналиши бўйлаб ўтилганда (4.9) тенглама қуйидагича ёзилади:
r1 i1 - r3 i3 - r2 i2 = е1 - е2 .

30. Харфлар билан белгиланаётган қийматлар, ўз ўрнида, мусбат ёки манфий бўлиши ҳам мумкин. Кирхгофнинг иккинчи қонуни ифодасидаги

Σr·i ва Σе йиғиндилар
контурнинг бир қисми учун ҳам, яъни а ва b нуқталар орасида узилиш
пайдо бўлганда ҳам қўлланилиши мумкин. Бундай ҳолда тенгламанинг
чап томонидаги узилган нуқталар орасидаги потенциаллар фарқи киритилади:
Σr·i+Uab= Σе,
(4.10)
бунда юқорида кўрилган ишоралаш қоидасидага амал қилинади.
Кейинги ифодани ташқи контур
(4.5-расм) учун қўллаб, соат мили
йўналиши билан ўтилганда, а нуқтасида ўтишни узиб b нуқтасида
ўтишни давом эттириб, қуйидагини аниқлаймиз:
r1i1 - r2i2 + Uab = е1 - е2 .
4.6-расм

31. Манбалар

Электротехникада манба деб хар қандай электр энергияси манбасига
айтилади.
Ток манбаси (идеал) – икки қутбли актив элемент, бунда ток кучи
қутбларнинг охирларида (зажим) кучланишга боғлиқ эмас.
Бунда идеал ток манбасининг ички қаршилиги чексиз деб олинади,
ва шунинг учун манбанинг токига манба нуқталарига (зажим) боғлиқ
кучланиш, ташқи электр занжирининг параметрларига таъсир
кўрсатмайди.
Идеал кучланиш генератори – унга уланган юкламадан қатъий назар
ўзгармас чиқиш кучланишига эга бўлган қурилма.
Бошқача қилиб айтганда хар қандай юкламада унинг кучланиши бир
хил.
Идеал ток генератори – хар қандай юкламада бир хил ток ишлаб
чиқувчи генератор.
Идеал кучланиш генераторининг ички қаршилиги нолга тенг, идеал
ток генераторининг ички ўтказувчанлиги нолга тенг.

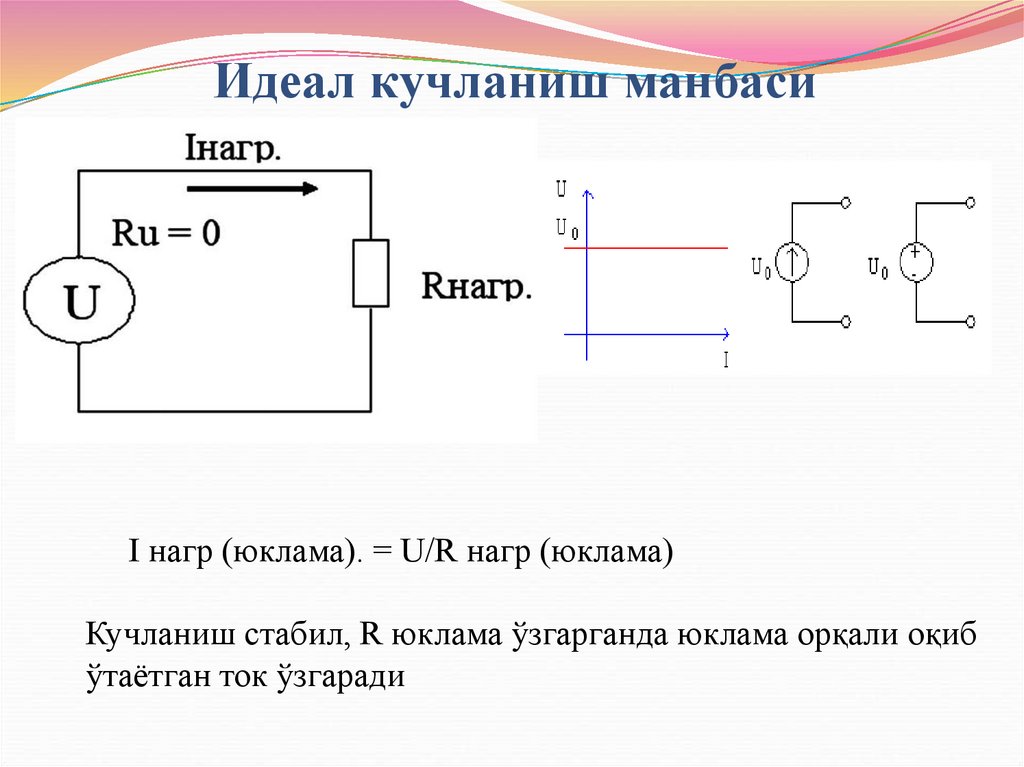
32. Идеал кучланиш манбаси

I нагр (юклама). = U/R нагр (юклама)
Кучланиш стабил, R юклама ўзгарганда юклама орқали оқиб
ўтаётган ток ўзгаради

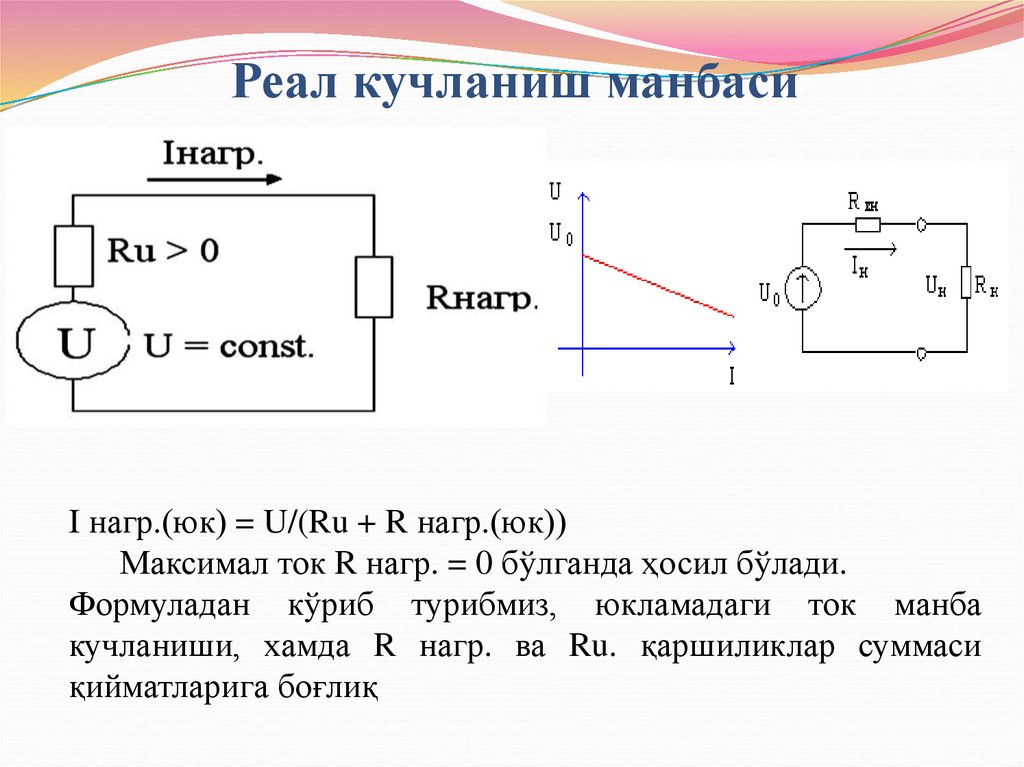
33. Реал кучланиш манбаси

I нагр.(юк) = U/(Ru + R нагр.(юк))
Максимал ток R нагр. = 0 бўлганда ҳосил бўлади.
Формуладан кўриб турибмиз, юкламадаги ток манба
кучланиши, хамда R нагр. ва Ru. қаршиликлар суммаси
қийматларига боғлиқ

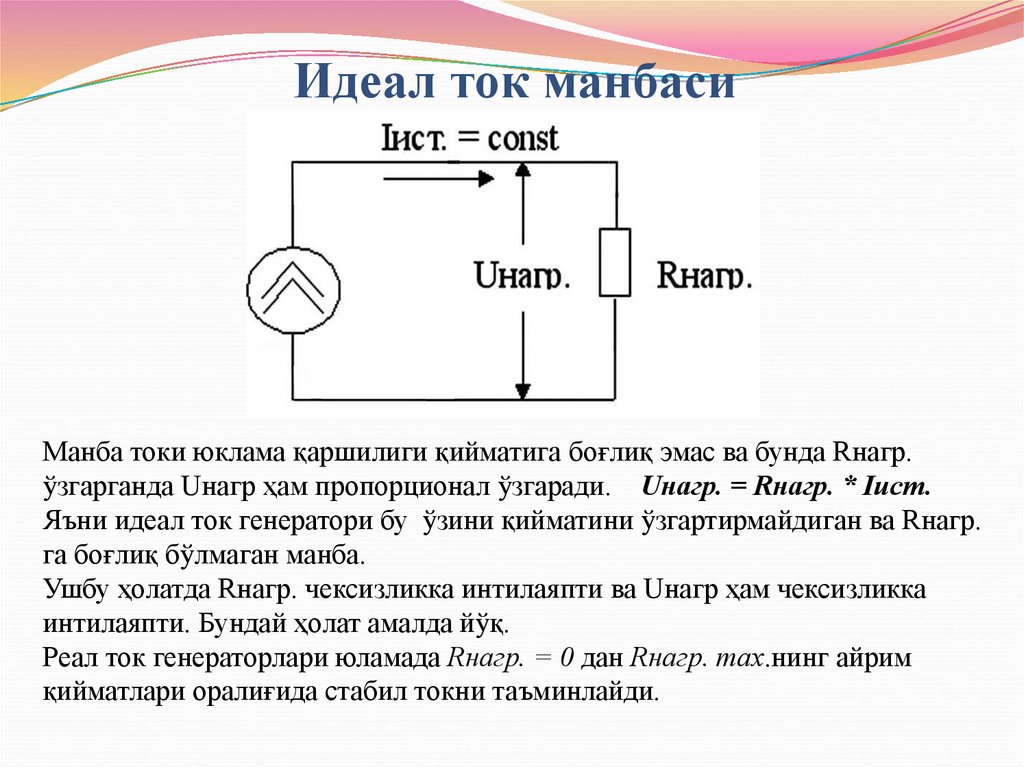
34. Идеал ток манбаси

Манба токи юклама қаршилиги қийматига боғлиқ эмас ва бунда Rнагр.
ўзгарганда Uнагр ҳам пропорционал ўзгаради. Uнагр. = Rнагр. * Iист.
Яъни идеал ток генератори бу ўзини қийматини ўзгартирмайдиган ва Rнагр.
га боғлиқ бўлмаган манба.
Ушбу ҳолатда Rнагр. чексизликка интилаяпти ва Uнагр ҳам чексизликка
интилаяпти. Бундай ҳолат амалда йўқ.
Реал ток генераторлари юламада Rнагр. = 0 дан Rнагр. max.нинг айрим
қийматлари оралиғида стабил токни таъминлайди.

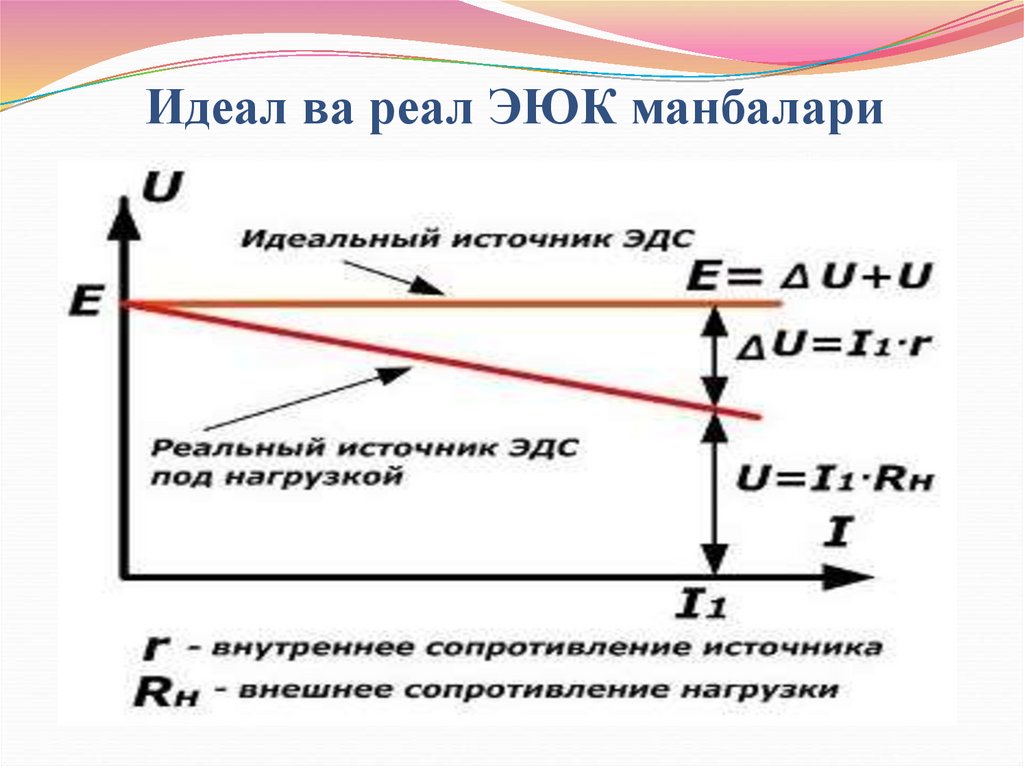
35. Идеал ва реал ЭЮК манбалари

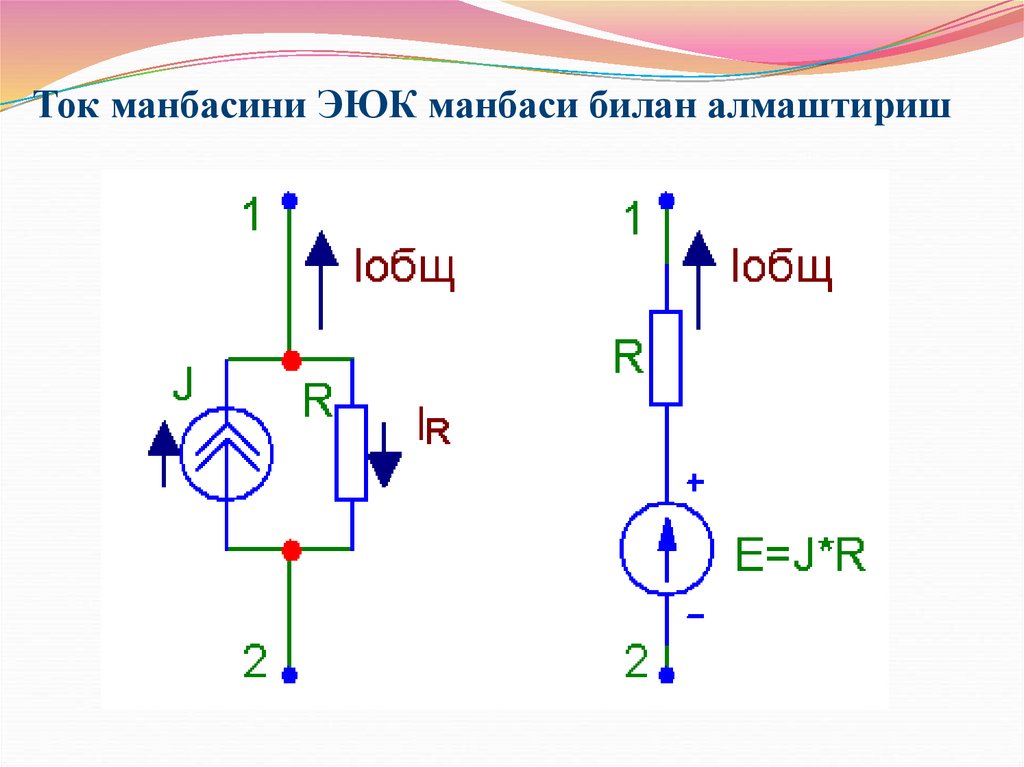
36. Ток манбасини ЭЮК манбаси билан алмаштириш

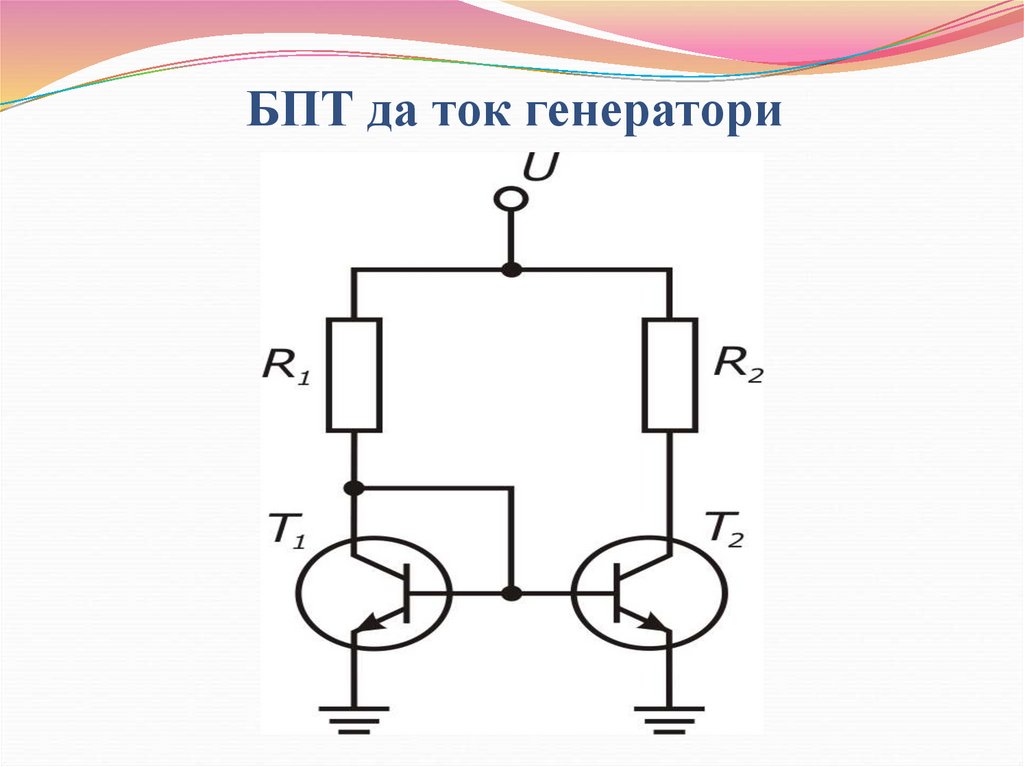
37. БПТ да ток генератори

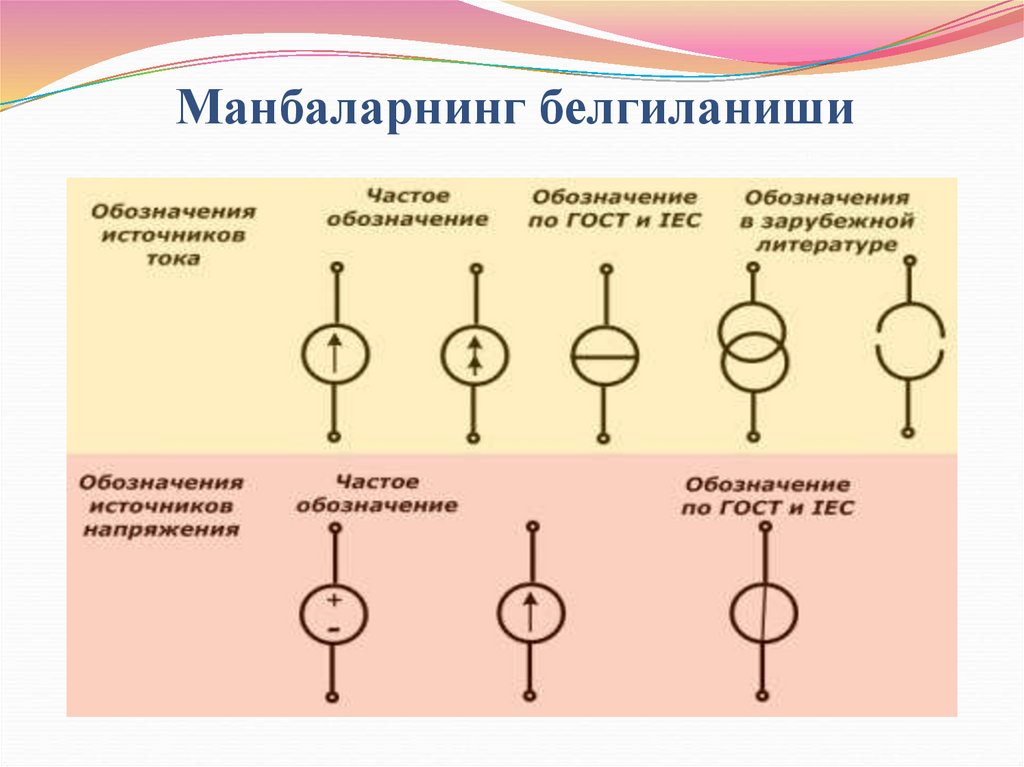
38. Манбаларнинг белгиланиши

39. Мустақил ва номустақил манбалар

Ҳамма актив элементлар мустақил ва номустақил
элементларга ажратилиши мумкин. Қийматлари
электр
занжирининг
бошқа
участкаларидаги
кучланиш ва токга боғлиқ бўлмаган кучланиш ва ток
ҳосил қилаётган манбалар мустақил дейилади.
Кучланиш ва ток қийматлари занжирнинг бошқа
участкаларидаги ток ва кучланишларга боғлиқ бўлса
номустақил манбалар дейилади.
Аввалги дарсликдан биз бошқарилувчи манбаларни
биламиз: (савол: қандай?)

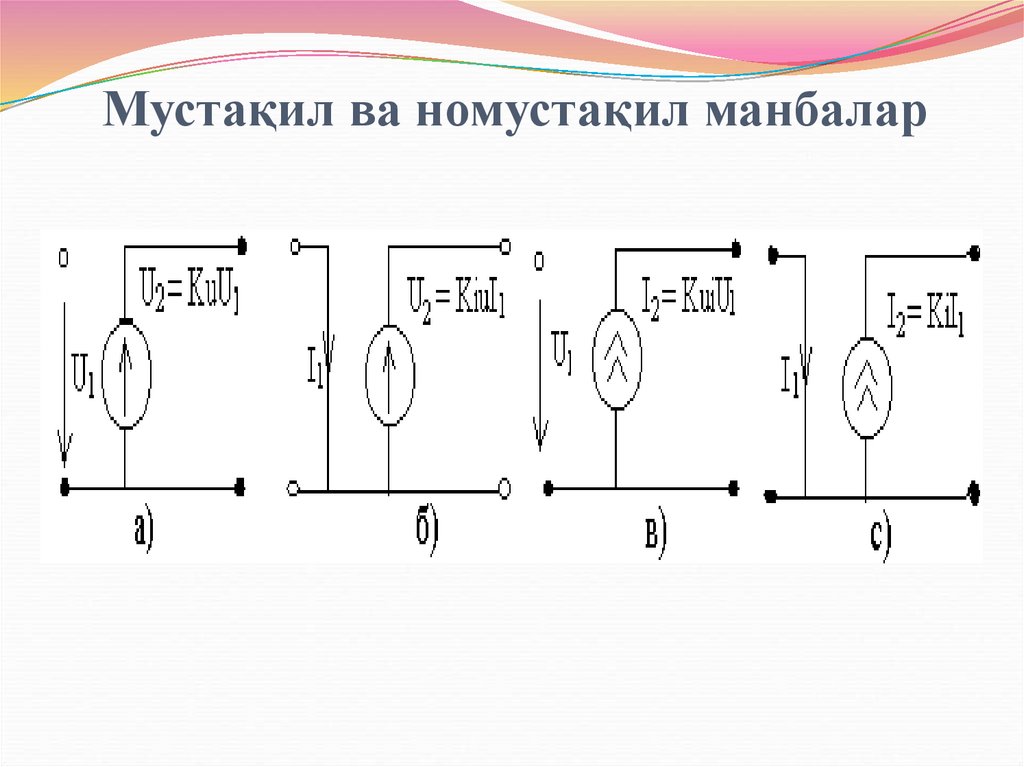
40. Мустақил ва номустақил манбалар

1.Кучланиш билан бошқарилувчи кучланиш манбаси
(КБКМ), параметри кучланиш бўйича узатиш коэффиценти Ku=U2m/U1m .
2.Ток билан бошқарилувчи кучланиш манбаси (ТБКМ),
параметри токни кучланишга айлантириш коэффиценти Kiu=U2m/I1m.
3.Кучланиш билан бошқарилувчи ток манбаси (КБТМ),
параметри кучланишни токга айлантириш коэффиценти Kui=I2m/U1m.
4.Ток билан бошқарилувчи ток манбаси (ТБТМ), параметри
ток бўйича узатиш коэффиценти - Ki=I2m/I1m.

41. Мустақил ва номустақил манбалар

42. Мустақил ва номустақил манбалар

43. Мустақил ва номустақил манбалар

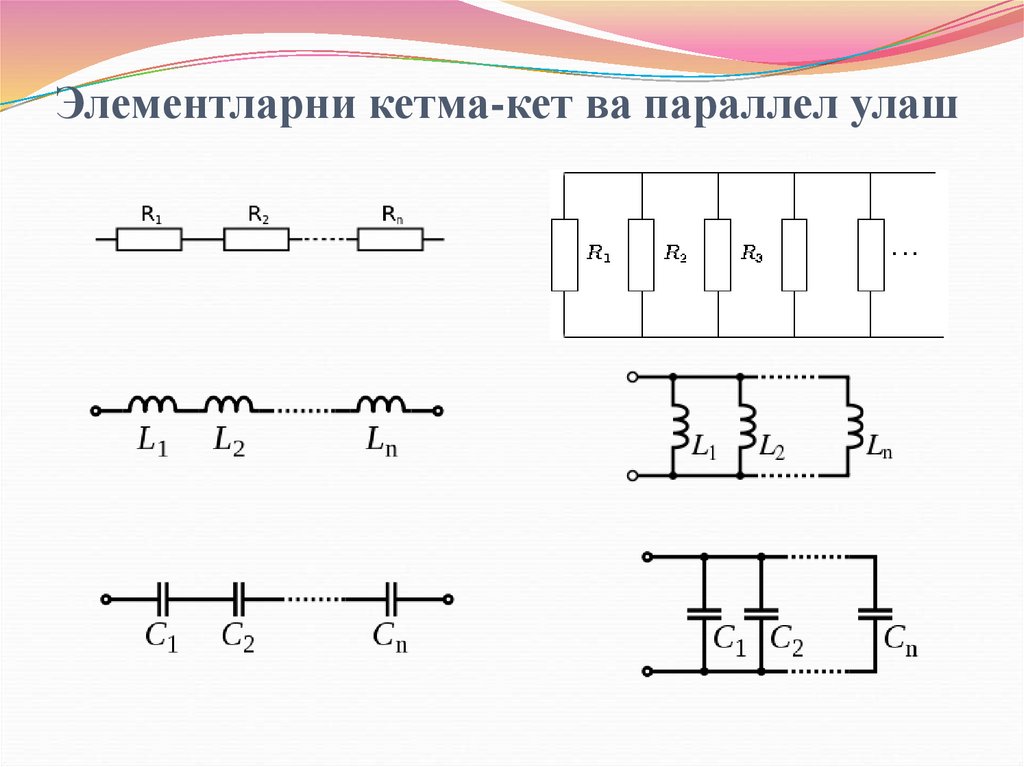
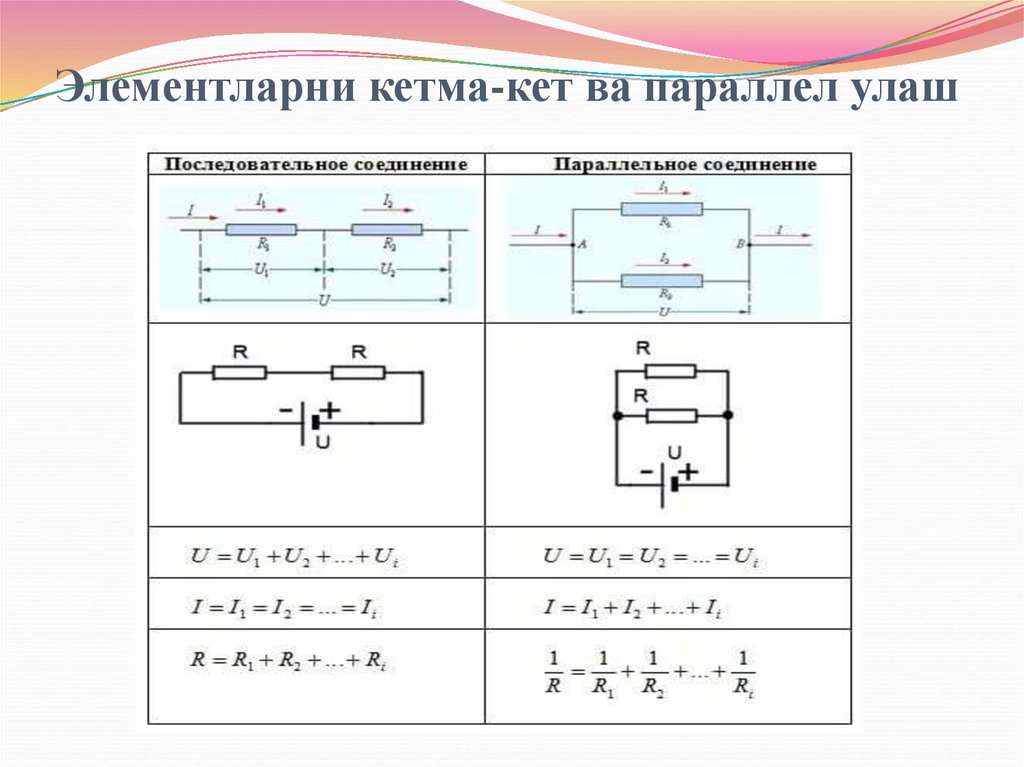
44. Элементларни кетма-кет ва параллел улаш

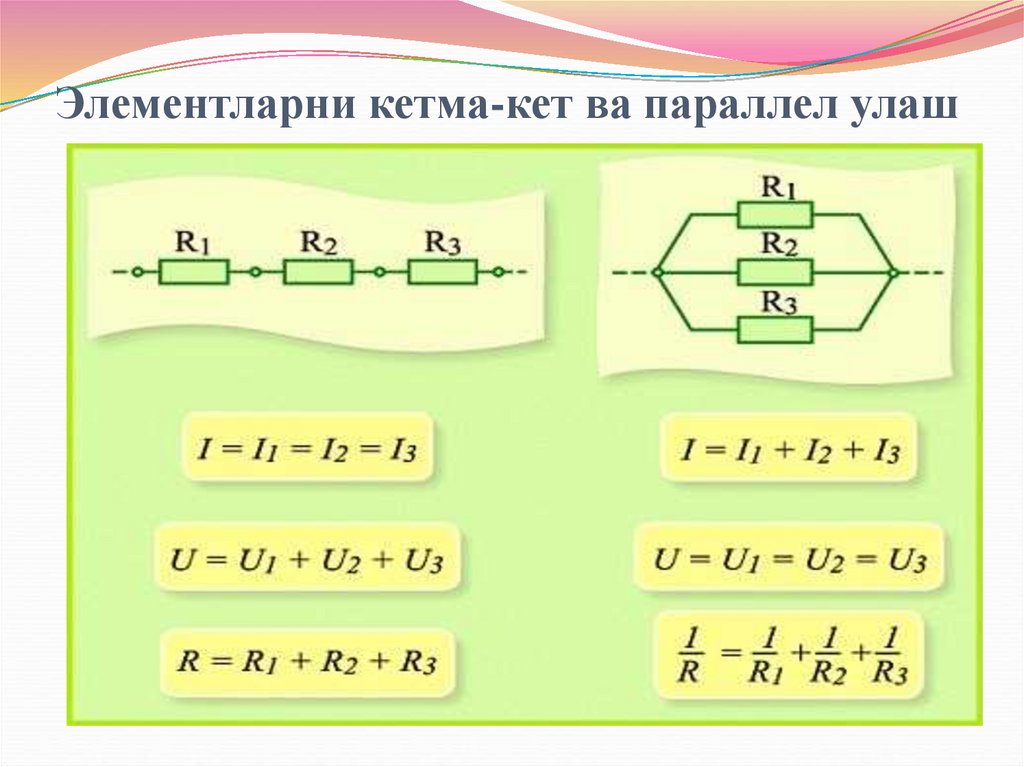
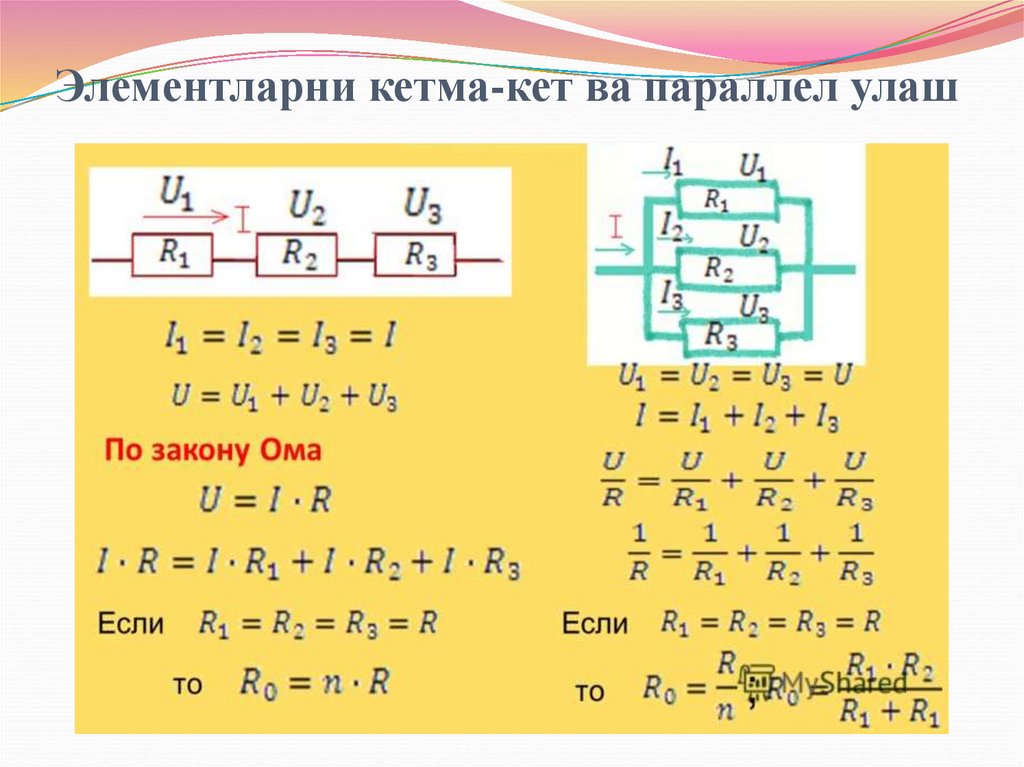
Ўтказгичлар
кетма-кет
уланганда
ҳамма
ўтказгичларнинг ток кучи тенг.
Бунда занжирнинг умумий кучланиши ўтказгич
охирларидаги хар бир кучланишлар суммасига тенг.
Параллел
уланганда
занжир
элементларини
бирлаштирувчи икки тугун орасидаги кучланиш
(тушиши) ҳамма элементлар учун бир хил.
Бунда занжирнинг умумий қаршилигига тескари
бўлган қиймат, ўтказгичларни параллел уланган
тескари қаршиликлари қийматлари суммасига тенг.

45. Элементларни кетма-кет ва параллел улаш

46. Элементларни кетма-кет ва параллел улаш

47. Элементларни кетма-кет ва параллел улаш

48. Элементларни кетма-кет ва параллел улаш

49. Элементларни кетма-кет ва параллел улаш

50. Назорат саволлари

1. Кирхгоф қонунлари (1) ва (2).
2. Кирхгоф қонунлари асосида электр занжирни
ҳисоблаш.
3. Манбалар.
4. Мустақил ва номустақил манбалар.
5. Элементларни кетма-кет ва параллел улаш.