Тема 2. СЛУ итерационные методы

1.

Андреева Анна Дмитриевна

2. Системы линейных алгебраических уравнений

a11x1 a12 x2 a1n xn f1
a x a x a x f
21 1 22 2
2n n
2
am1 x1 am 2 x2 amn xn f m
Аx f
m – количество уравнений системы
n – количество неизвестных системы
матрица коэффициентов
a11 a12
a
a22
21
A
am1 am 2
a1n
a2 n
amn
x1
x
x 2
xn
f1
f
f 2
fm
вектор неизвестных
заданный вектор

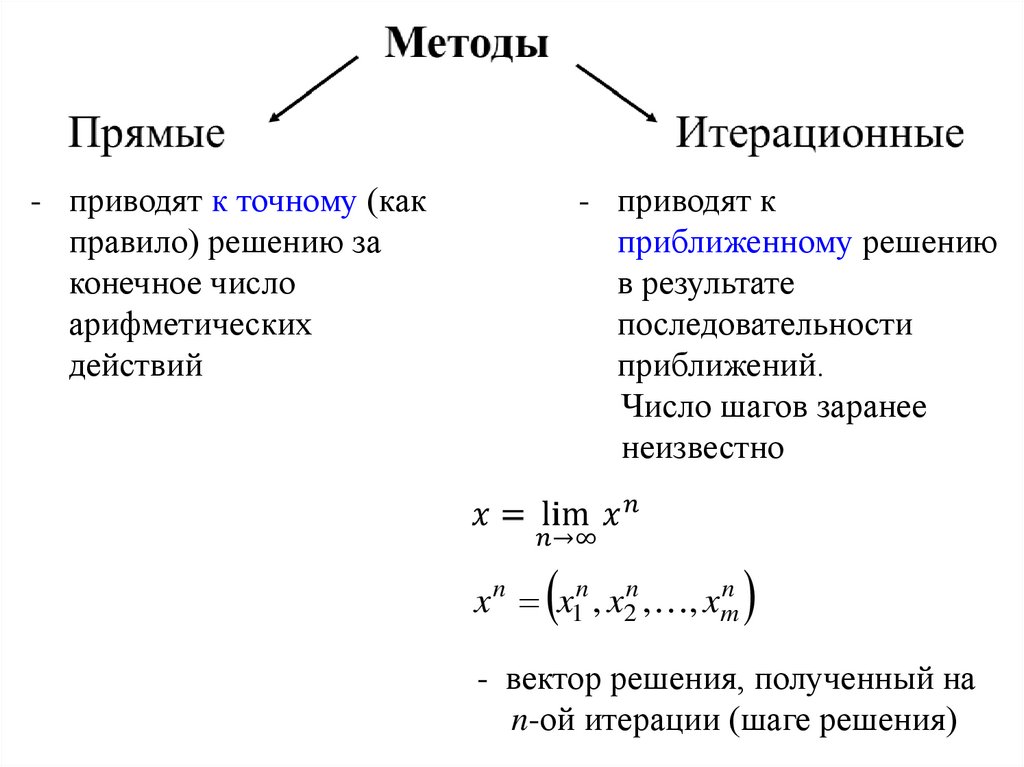
3.

- приводят к точному (как
правило) решению за
конечное число
арифметических
действий
- приводят к
приближенному решению
в результате
последовательности
приближений.
Число шагов заранее
неизвестно
x n x1n , x2n , , xmn
- вектор решения, полученный на
n-ой итерации (шаге решения)

4. Итерационные методы решения систем линейных уравнений

rang A = rang A|f =m
Аx f
- СЛАУ определённая
(имеет единственное
решение)
a11 x1 a12 x2 a1m xm f1
a x a x a x f
21 1
22 2
2m m
2
a m1 x1 a m 2 x2 a mm xm f m
- вектор решения, полученный на
x 0 x10 , x20 , , xm0
x n x1n , x2n , , xmn
- начальное приближение
(заданный вектор)
n-ой итерации
0 1
- точность решения (задана)
1

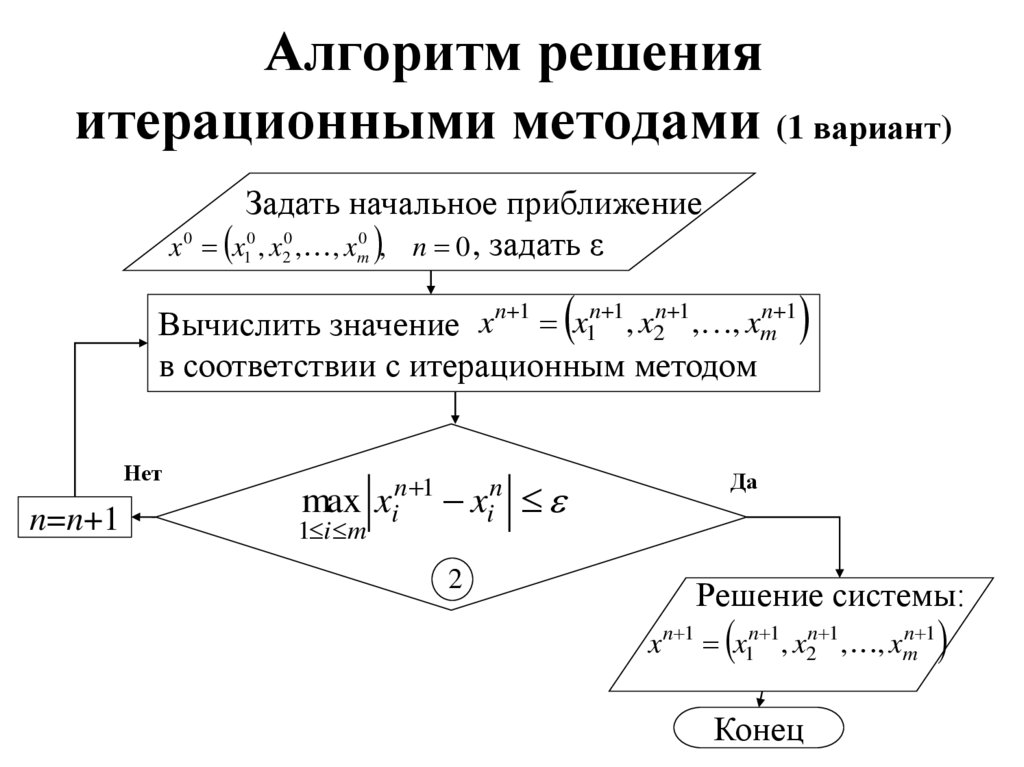
5. Алгоритм решения итерационными методами (1 вариант)

Задать начальное приближение
x 0 x10 , x20 , , xm0 , n 0 , задать ε
Вычислить значение x n 1 x1n 1, x2n 1, , xmn 1
в соответствии с итерационным методом
Нет
n=n+1
max xin 1 xin
1 i m
2
Да
Решение системы:
x n 1 x1n 1 , x2n 1, , xmn 1
Конец

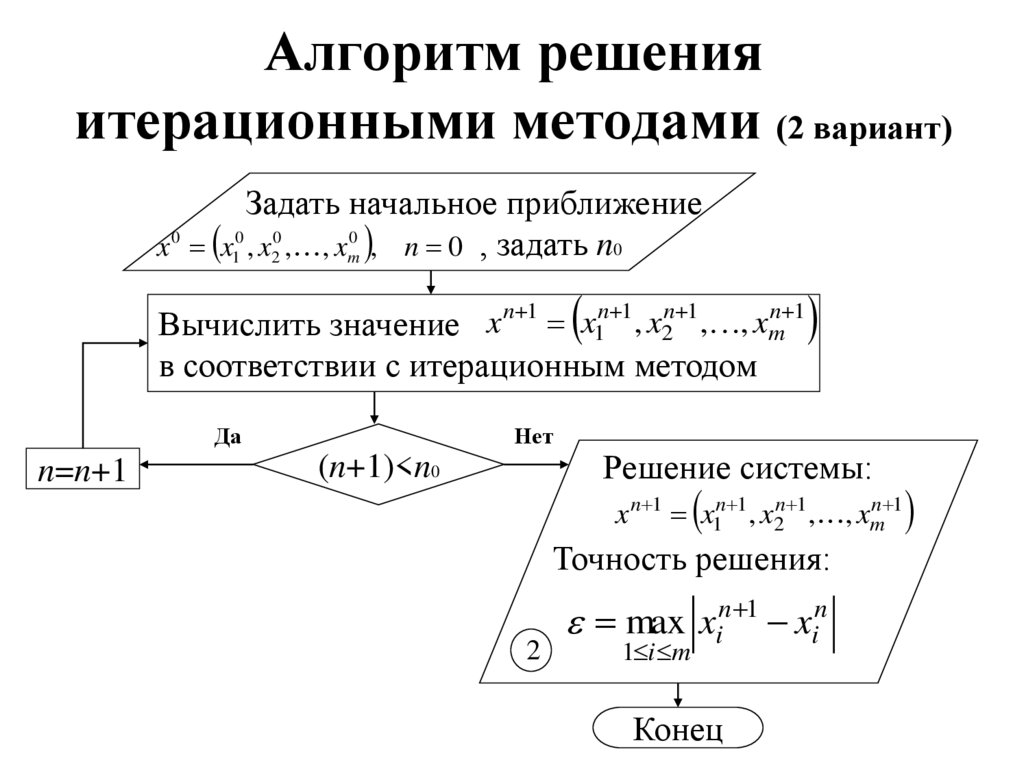
6. Алгоритм решения итерационными методами (2 вариант)

Задать начальное приближение
x 0 x10 , x20 , , xm0 , n 0 , задать n0
Вычислить значение x n 1 x1n 1, x2n 1, , xmn 1
в соответствии с итерационным методом
Да
n=n+1
Нет
(n+1)<n0
Решение системы:
x n 1 x1n 1 , x2n 1, , xmn 1
Точность решения:
2
max xin 1 xin
1 i m
Конец

7. Методы решения

ai1 x1 ai,i 1 xi 1 aii xi ai ,i 1 xi 1 aim xm f i , i 1, m
i 1 j m
1 j i 1
3
j m a
f i j i 1 aij
ij
xi
xj
x j , i 1, m
aii
j 1 aii
j i 1 aii
Метод Якоби:
4
j i 1 a
j m a
j m a
f
f
ij
ij
ij n
xin 1 i
x nj
x nj i
x j , i 1, m
aii
aii
j 1 aii
j i 1 aii
j 1, j i aii
Метод Зейделя: 5
xin 1
f i j i 1 aij n 1 j m aij n
xj
x j , i 1, m
aii
j 1 aii
j i 1 aii

8. Матричная форма записи итерационных методов

Аx f
Матричная форма записи
итерационных методов
A A1 D A2
6
a11 a12 aj1 mi 1
j m a
a
f
ij
ij n
n
a x n a1 i a
x
xj ,
21 i
22
2m
j
A
aii
aii
aii
j
1
j
i
1
i
1
,
m
a m1 a m 2 a mm
0 0 0
a
0 0
21
A1
a
a
0
m1 m 2
1 a 0 0
00
11
a
11
n 1
1
1
n
1
n
X
D f D A1 X D A2 X
00
0 01 a 22
1
D
a
D
22
j i 1 a
j m a
0
0
a
f
ij n 1
ij n
0
1mm
0
xin 1 i
xj
xj ,
a mm
aii
a
j 1
ii
a
j i 1 ii
i 1, m
X n 1 D 1 f D 1 A1 X n 1 D 1 A2 X n
0 a12 a1m
0 0 a
2m
A2
0 0 0

9. Матричная форма записи итерационных методов

Матричная форма записи
Аx f
итерационных методов
X n 1 D 1 f D 1 A1 X n D 1 A2 X n
A A1 D A2
*D
DX n 1 A1 A2 X n f
D( X
n 1
X ) AX f
X n 1 D 1 f D 1 A1 X n 1 D 1 A2 X n
( D A1 ) X n 1 A2 X n f
n
n
4.1
*D
5.1
( D A1 )( X n 1 X n ) AX n f

10. Каноническая форма одношаговых итерационных методов

Аx f
Bn 1
X
Метод сходится, если
n 1
X
n 1
n
AX n f
X n 1 X n 0, n
Явный метод, если Bn+1=E
Неявный метод, если Bn+1≠ E
Cтационарный метод, если B = const, τ = const
Нестационарный метод, если B ≠ const или τ ≠ const
7

11. Другие итерационные методы

Метод простой
итерации
X n 1 X n
X n 1 X n
Метод Ричардсона
Метод верхней
релаксации
xin 1
j i 1 a
ij
j 1
ii
a
AX n f
n 1
( D A1 )
AX n f
X n 1 X n
x nj 1 1 xin
j m a
a
ij
j i 1 ii
AX n f
x nj
fi
, i 1, m
aii

12. Исследование сходимости итерационных методов

Аx f
Исследование сходимости
итерационных методов
B
X n 1 X n
AX n f
Итерационный метод сходится, если
X n X 0, n
X n 1 X n 0, n
x
j m
2
x
j
j 1

13. Матричные неравенства

Для любой действительной квадратной матрицы Cm×m
*
C 0
C x, x 0, x X m , x 0
Доказано, что 0 : C x, x x
* C 0
C x, x 0, x X m , x 0
C
1
?
2
C 1

14. Теорема о сходимости итерационных методов

Теорема. Пусть А – симметричная положительно-определенная
матрица, τ > 0; и пусть справедливо матричное неравенство
В - 0.5 τ А > 0,
тогда итерационный метод сходится.
1. Метод Якоби
D( X n 1 X n ) AX n f
Следствие 1. Пусть А – симметричная положительно-определенная
j m
матрица с диагональным преобладанием:
тогда итерационный метод Якоби сходится.
aii aij , i 1, m ;
j 1,
j i
Условие сходимости: A < 2D
8

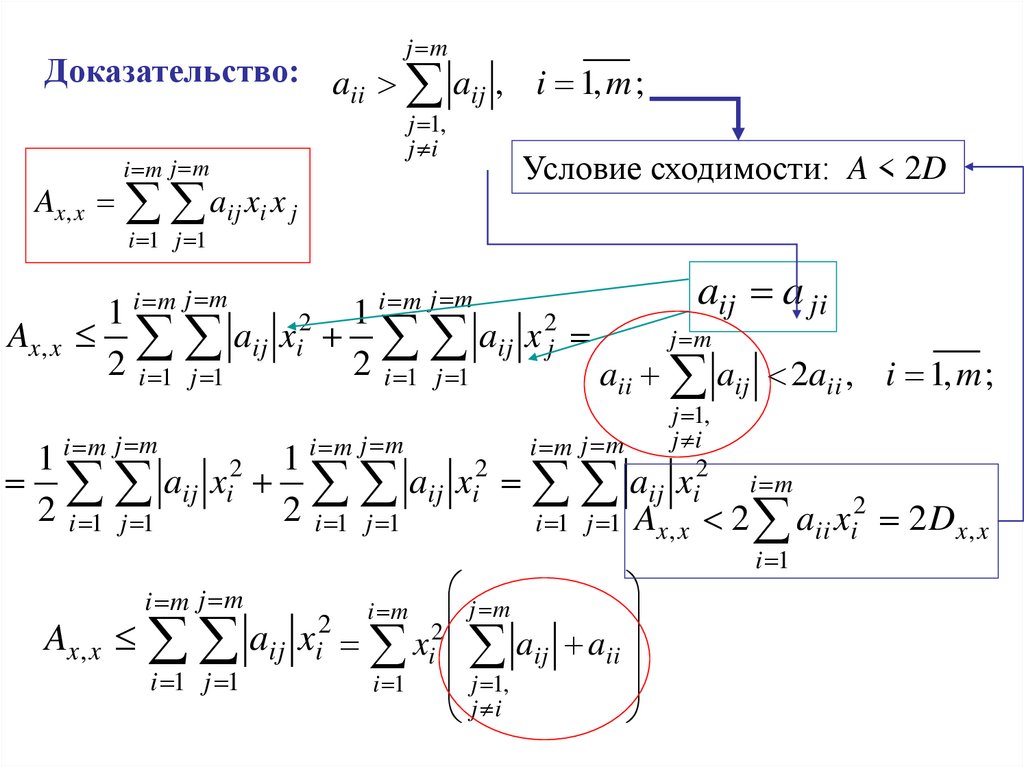
15.

j m
Доказательство: a
aij , i 1, m ;
ii
j 1,
j i
i m j m
Ax, x aij xi x j
Условие сходимости: A < 2D
i 1 j 1
i m j m
aij a ji
i m j m
1
1
2
Ax, x aij xi aij x 2j
j m
2 i 1 j 1
2 i 1 j 1
aii aij 2aii , i 1, m ;
j 1,
j i
i m j m
i m j m
i m j m
1
1
2
aij xi
aij xi2
aij xi2 i m
2 i 1 j 1
2 i 1 j 1
aii xi2 2 Dx, x
i 1 j 1 Ax , x 2
j m
2
2
Ax, x
aij xi xi aij aii
j 1,
i 1 j 1
i 1
j i
i m j m
i m
i 1

16.

2. Метод верхней релаксации
( D A1 )
X n 1 X n
AX n f
Следствие 2. Пусть А – симметричная положительно-определенная
матрица, тогда итерационный метод верхней релаксации сходится,
при условии 0 < ω < 2
Доказательство:
A A1 D A2
B D A1
Ax, x A1x, x Dx, x A2 x, x Dx, x 2 A1x, x
В - 0.5 τ А > 0
Bx, x 0.5 Ax, x D A1 x, x 0.5 Dx, x 2 A1 x, x
1 0.5 Dx, x 0
>0
>0
0<ω<2

17.

X n 1 X n
3. Метод простой итерации
AX n f
Пусть А – симметричная положительно-определенная матрица,
тогда итерационный метод простой итерации сходится, при условии
min 0
E - 0.5 τ A > 0
i 1 0.5 iA , i 1, m
?
Матрица A положительно-определенная:
!
0, i 1, m
A
i
1A 2A mA собственные значения матрицы A
A
max
min 1 0.5
A
max
0
2
A
max