Week 2 Ls 1-3 (1)

1. Economics

Week 2. Lessons 1-3

2. Learning objectives

• Understand the formula of
calculation deposit
profitability and loan
payments.
• Calculate deposit profitability
and loan payments using
simple and compound
interest.

3. Discuss

If you put $100 in a bank at 5%
per year, how much will you
have after 1 year?

4. Interest

Interest is the amount of money a
lender or financial institution
receives for lending out money.
“Interest” is defined as the cost of
borrowing money.

5. Simple and Compound Interest

• Simple interest – interest is paid only
on the principal.
“Principal” refers to the original sum of
money borrowed in a loan or put into
an investment.
• Compound interest is paid on both
principal and interest, compounded at
regular intervals.

6. Simple Interest Formula

Simple interest = P×i×n
where:
P=Principal
i=interest rate
n=term of the loan (in years)
Simple Interest
Formula

7. Example

Example: a $1000 principal paying 10%
simple interest after 3 years pays.
1000$ ×0.1 ×3 = $300
Simple interest = P×i×n
(0.1= 10%:100)
where:
P=Principal
i=interest rate
n=term of the loan (in years)

8. Compound interest

If interest is compounded annually, it pays
0.1 × $1000 = $100 the first year,
0.1 × $1100 = $110 the second year and
0.1 × $1210 = $121 the third year
totaling $100 + $110 + $121 = $331 interest

9. Compound Interest Formula

FV = the compound amount or future value
P = principal
i = interest rate per period of compounding
n = number of periods
I = interest earned

10. Activity 1

• Example: $800 is invested at 7% for 6
years. Find the simple interest and the
interest compounded annually.
• Simple interest:
• Compound interest:

11. Solution

• Example: $800 is invested at 7% for 6 years. Find
the simple interest and the interest compounded
annually.
• Simple interest: FV=PV*i*n
• Compound interest:

12. Compounding periods

• In the formula for calculating compound
interest, the variables "i" and "n" have to be
adjusted if the number of compounding
periods is more than once a year.
• For example, for a 10-year loan at 10%,
where interest is compounded semi-annually
(number of compounding periods = 2), i =
5% (i.e., 10% / 2) and n = 20 (i.e., 10 x 2).

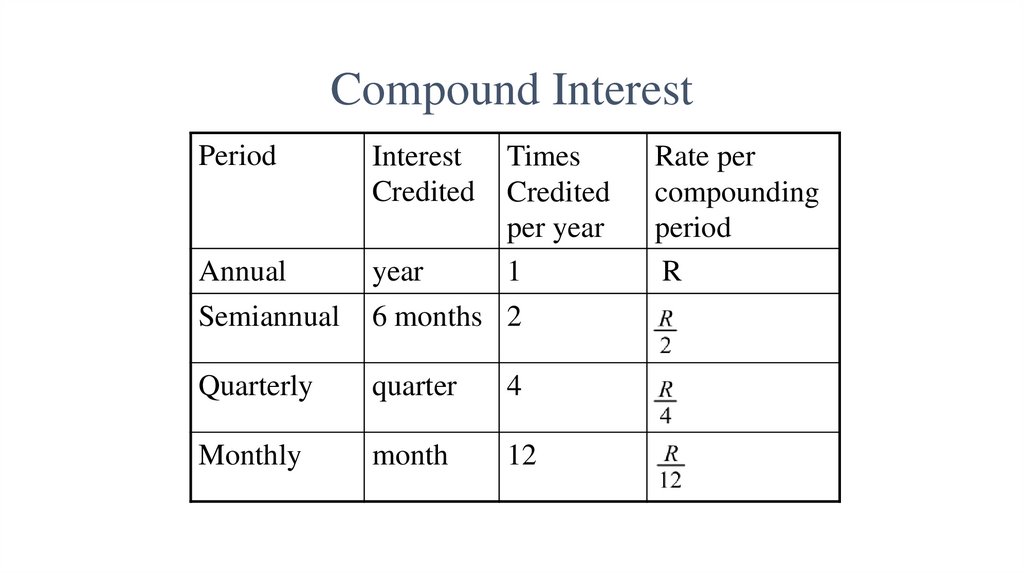
13. Compound Interest

Period
Interest
Credited
Annual
year
Semiannual
6 months 2
Quarterly
quarter
4
Monthly
month
12
Times
Credited
per year
1
Rate per
compounding
period
R

14. Compound Interest

where:
i=interest rate in percentage terms
n=number of compounding periods per year
t=total number of years for the investment or loan
Example: $32000 is invested at 10% for 2 years. Find the
interest compounded monthly:

15. Activity 1

Example: $32000 is invested at 10% for 2
years. Find the interest compounded yearly,
semiannually, quarterly, and monthly:

16. Answer

• Example: $32000 is invested at 10% for 2 years.
Find the interest compounded yearly,
semiannually, quarterly, and monthly.
yearly:
semiannually:

17.

quarterly
monthly

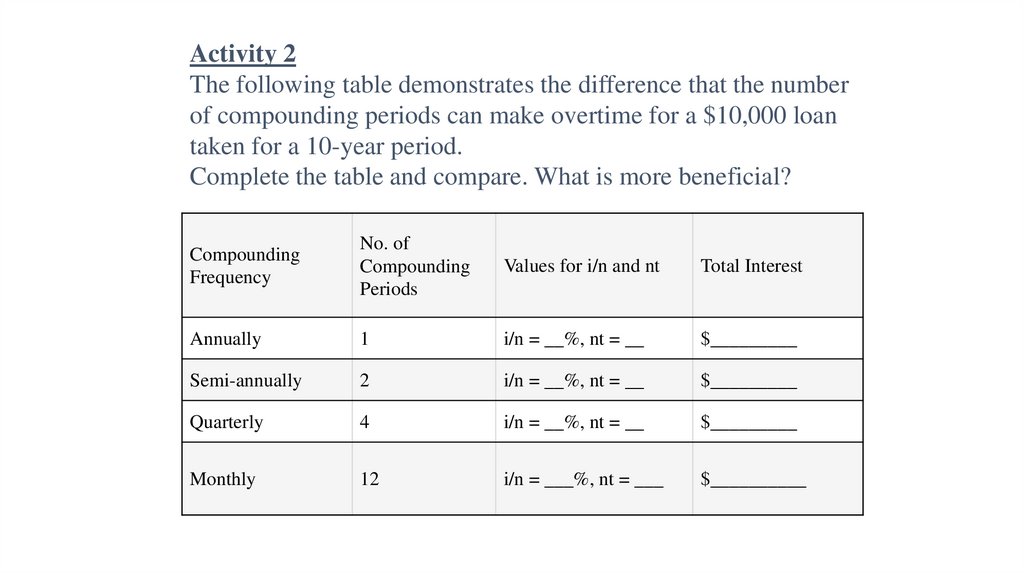
18. Activity 2 The following table demonstrates the difference that the number of compounding periods can make overtime for a

$10,000 loan
taken for a 10-year period.
Complete the table and compare. What is more beneficial?
Compounding
Frequency
No. of
Compounding
Periods
Values for i/n and nt
Total Interest
Annually
1
i/n = __%, nt = __
$_________
Semi-annually
2
i/n = __%, nt = __
$_________
Quarterly
4
i/n = __%, nt = __
$_________
Monthly
12
i/n = ___%, nt = ___
$__________

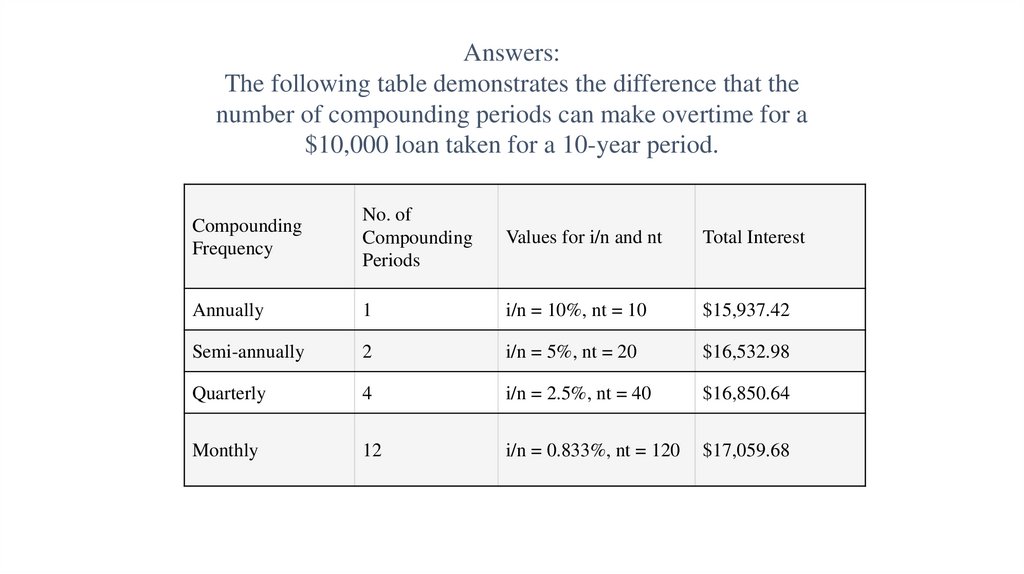
19. Answers: The following table demonstrates the difference that the number of compounding periods can make overtime for a $10,000

loan taken for a 10-year period.
Compounding
Frequency
No. of
Compounding
Periods
Values for i/n and nt
Total Interest
Annually
1
i/n = 10%, nt = 10
$15,937.42
Semi-annually
2
i/n = 5%, nt = 20
$16,532.98
Quarterly
4
i/n = 2.5%, nt = 40
$16,850.64
Monthly
12
i/n = 0.833%, nt = 120
$17,059.68

20. Daily and Continuous Compounding

• Daily compound interest formula: divide i by 365
and multiply n by 365

21. Activity Daily and Continuous Compounding

• Example: Find the compound amount if
$2900 is deposited at 5% interest for 10
years if interest is compounded daily.

22. Solution

• Example: Find the compound amount if $2900 is
deposited at 5% interest for 10 years if interest is
compounded daily.

23. Formative assessment

Worksheet 1