механика жидкостей и газов

1.

МЕХАНИКА ЖИДКОСТЕЙ И ГАЗОВ

2.

ОБЩИЕ СВОЙСТВА ЖИДКОСТЕЙ И ГАЗОВ
Гидроаэромеханика – раздел физики, изучающий механические свойства жидкостей и
газов, их взаимодействие между собой и с граничащими с ними твердыми телами
В отличие от молекулярно-кинетической теории жидкостей и газов гидроаэромеханика
заменяет действительную молекулярную структуру жидкостей и газов
идеализированными представлениями о материальной среде, обладающей двумя
основными свойствами — сплошностью (непрерывностью) и легкой подвижностью
(текучестью). При этом жидкости считают практически несжимаемыми.
Гидростатика изучается
равновесие
жидкости и
воздействие
покоящейся
жидкости на
погружённые в неё
тела. Изучение
распределения
давления в
жидкости.
Гидродинамика движение со
скоростью, много
меньшей скорости
звука.
При таких
скоростях
сжимаемости
среды не
происходит и
плотность
вещества
считается
постоянной
Газовая
динамика - если
скорость движения
тела
приблизительно
равна скорости
звука или
превышает её.
Аэромеханика изучение
движения тел и
летательных
аппаратов в
атмосфере.
2

3.

ОБЩИЕ СВОЙСТВА ЖИДКОСТЕЙ И ГАЗОВ
Свойства жидкостей и газов - способность принимать форму сосуда
не обладают упругостью формы
обладают упругостью объема
это агрегатное состояние
вещества, в котором сохраняется объем,
образуется поверхность, принимает
форму сосуда, в котором находится.
это агрегатное состояние
вещества, в котором расстояния между
молекулами велики, а силы
взаимодействия пренебрежимо малы.
Молекулы газа движутся практически
свободно, газ полностью заполняет весь
предоставленный ему объем.
очень малая сжимаемость
чтобы увеличить плотность воды на 1%,
необходимо давление 200 атм. При
таком давлении вылетающая струя воды
будет иметь скорость
v = 200 м/с
сжимаются очень легко
чтобы увеличить плотность воздуха на
1%, необходимо давление 0,02 атм. При
таком давлении вылетающая струя воды
будет иметь скорость
v = 100 м/с
Несжимаемая жидкость – жидкость, плотность которой всюду одинакова, не
изменяется со временем и не зависит от давления
3

4.

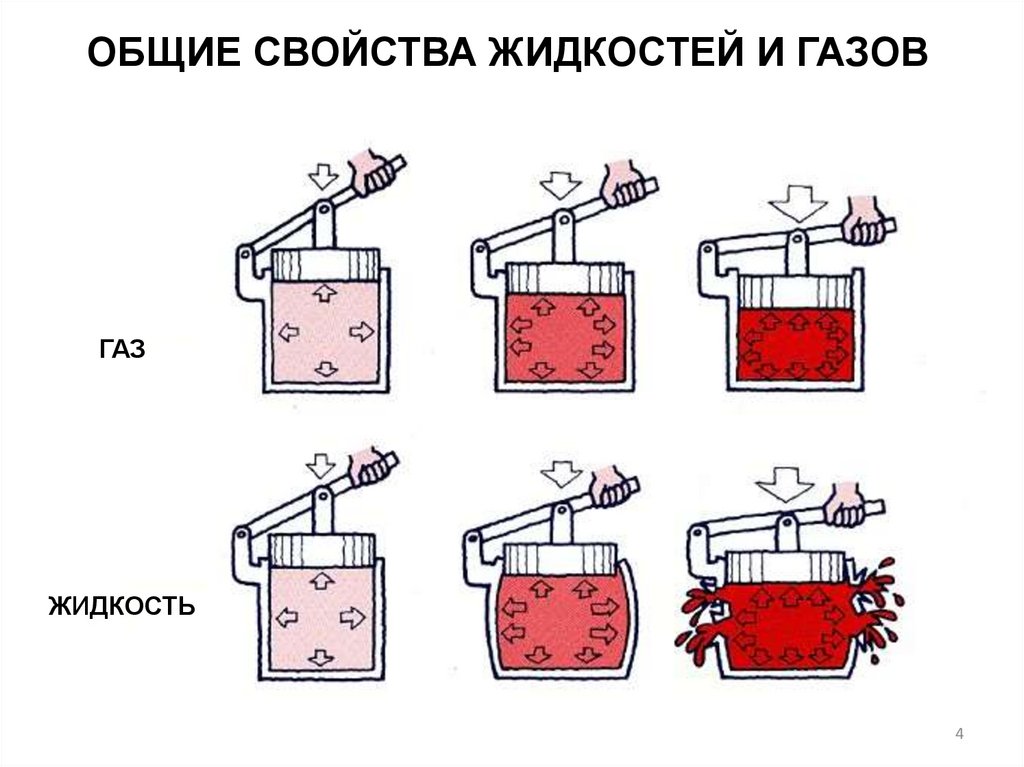
ОБЩИЕ СВОЙСТВА ЖИДКОСТЕЙ И ГАЗОВ
ГАЗ
ЖИДКОСТЬ
4

5.

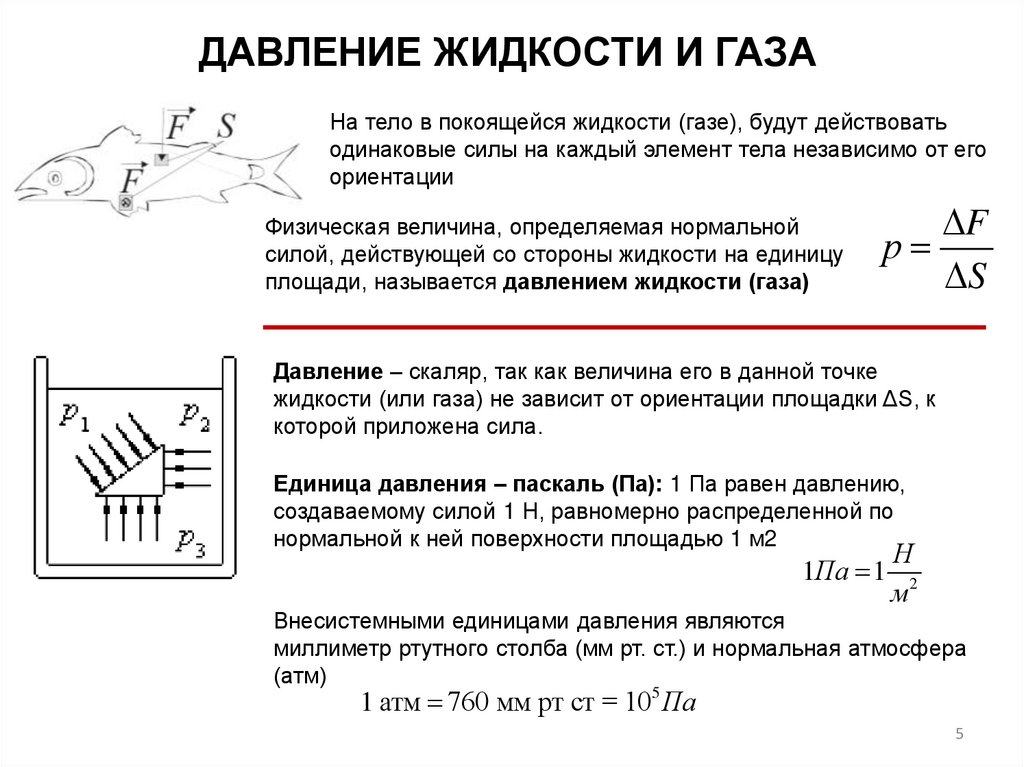
ДАВЛЕНИЕ ЖИДКОСТИ И ГАЗА
На тело в покоящейся жидкости (газе), будут действовать
одинаковые силы на каждый элемент тела независимо от его
ориентации
Физическая величина, определяемая нормальной
силой, действующей со стороны жидкости на единицу
площади, называется давлением жидкости (газа)
F
р
S
Давление – скаляр, так как величина его в данной точке
жидкости (или газа) не зависит от ориентации площадки ΔS, к
которой приложена сила.
Единица давления – паскаль (Па): 1 Па равен давлению,
создаваемому силой 1 Н, равномерно распределенной по
нормальной к ней поверхности площадью 1 м2
1Па 1
Н
м2
Внесистемными единицами давления являются
миллиметр ртутного столба (мм рт. ст.) и нормальная атмосфера
(атм)
1 атм 760 мм рт ст = 105 Па
5

6.

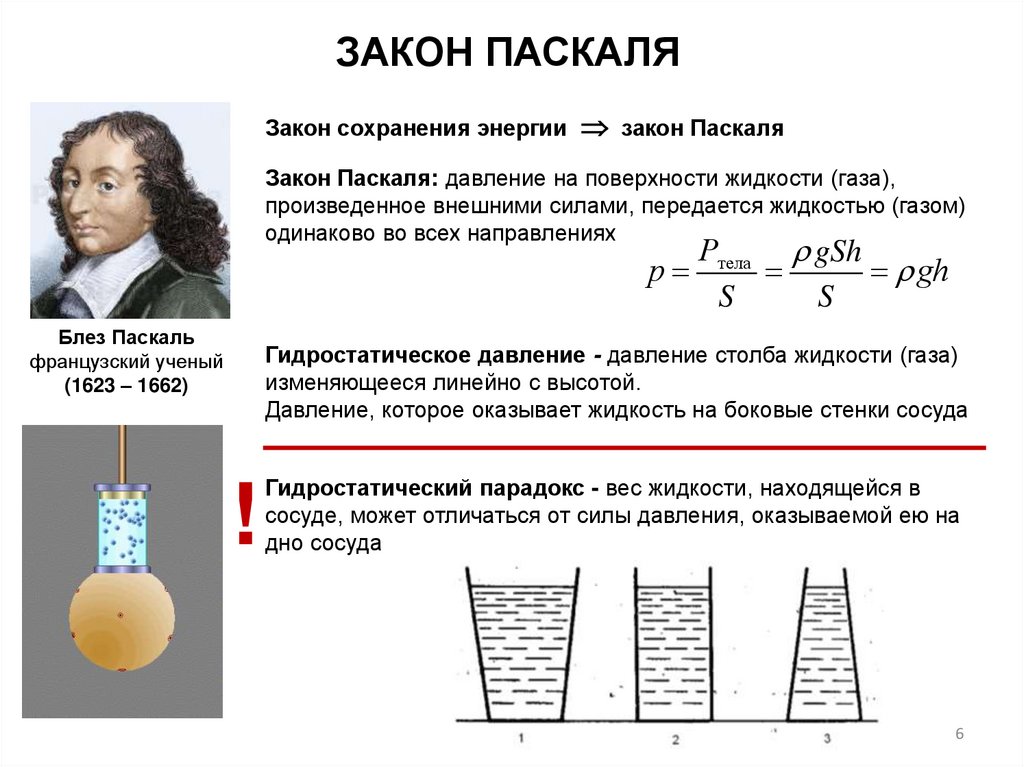
ЗАКОН ПАСКАЛЯ
Закон сохранения энергии закон Паскаля
Закон Паскаля: давление на поверхности жидкости (газа),
произведенное внешними силами, передается жидкостью (газом)
одинаково во всех направлениях
Ртела gSh
р
gh
S
S
Блез Паскаль
французский ученый
(1623 – 1662)
Гидростатическое давление - давление столба жидкости (газа)
изменяющееся линейно с высотой.
Давление, которое оказывает жидкость на боковые стенки сосуда
!
Гидростатический парадокс - вес жидкости, находящейся в
сосуде, может отличаться от силы давления, оказываемой ею на
дно сосуда
6

7.

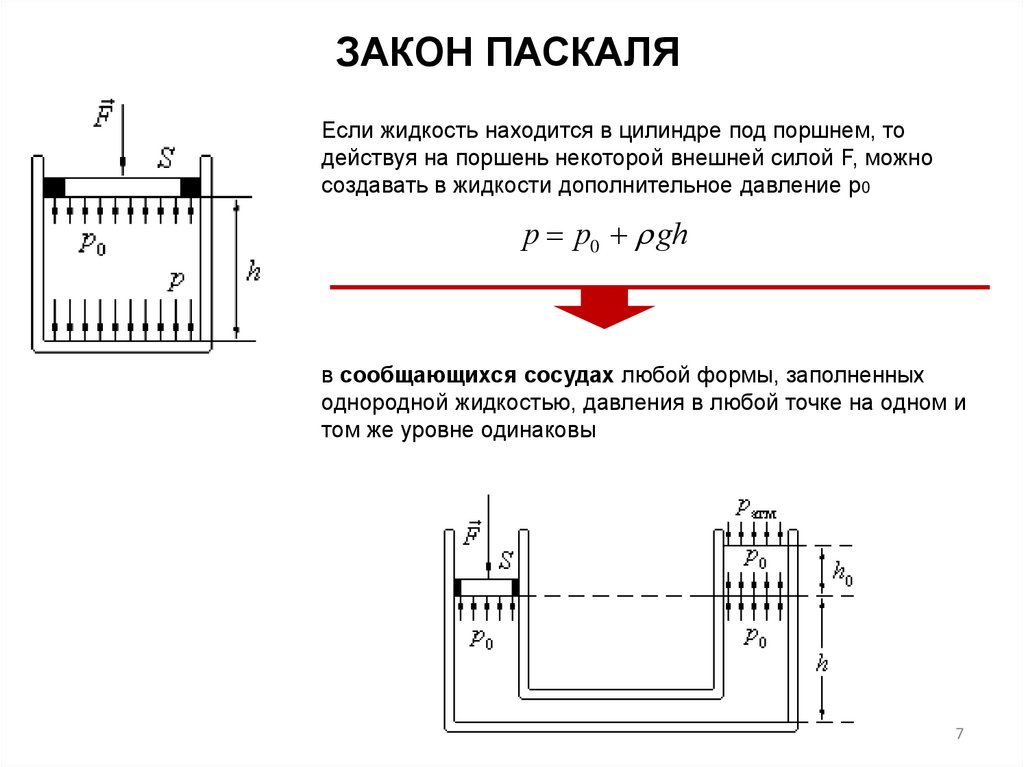
ЗАКОН ПАСКАЛЯ
Если жидкость находится в цилиндре под поршнем, то
действуя на поршень некоторой внешней силой F, можно
создавать в жидкости дополнительное давление р0
р р0 gh
в сообщающихся сосудах любой формы, заполненных
однородной жидкостью, давления в любой точке на одном и
том же уровне одинаковы
7

8.

ЗАКОН ПАСКАЛЯ
Если вертикально расположенные цилиндры сообщающихся сосудов закрыть
поршнями, то с помощью внешних сил, приложенных к поршням, в жидкости можно
создать большое давление p, во много раз превышающее гидростатическое давление
ρgh в любой точке системы.
Если поршни имеют разные площади S1 и S2, то на них со стороны жидкости действуют
разные силы
F1 pS1
F2 pS2
Такие же по модулю, но противоположно направленные внешние силы должны быть
приложены к поршням для удержания системы в равновесии
F1 F2
р
S1 S2
n
S2
S1
F1h1 F2 h2
!
Устройства такого рода называют гидравлическими машинами.
Они позволяют получить значительный выигрыш в силе, но
проигрыш в расстоянии
Это правило выполняется для любых
идеальных машин, где нет силы трения.
Гидравлические машины, используемые
для подъема грузов, называются
домкратами. Они применяются в качестве
гидравлических прессов. В качестве
жидкости используются минеральные
масла.
8

9.

ЗАКОН АРХИМЕДА
на погруженное в жидкость или газ тело действуют силы: вес тела
и противоположно направленная, выталкивающая сила, обусловленная
гидростатическим давлением жидкости
тело находиться в равновесии в жидкости
На тело, погруженное в жидкость (или газ), действует со стороны
жидкости (или газа) подъемная сила, направленная вверх и
приложенная к центру тяжести погруженного тела.
Архимед
древнегреческий
ученый
(287-212 годы до
нашей эры)
Величина этой силы равна весу вытесненной жидкости. В этой
формулировке, предполагается наличие тяготения, так как
существование выталкивающей силы обусловлено разностью
статистических давлений в жидкости (или газе).
Закон Архимеда: на тело, погруженное в жидкость (газ), действует
со стороны этой жидкости (газа) направленная вверх
выталкивающая сила, равная весу вытесненной телом жидкости
(газа):
FA Ж gV
Увеличение плотности жидкости приводит к увеличению
выталкивающей силы, и к уменьшению веса тела, погруженного в
9
жидкость.

10.

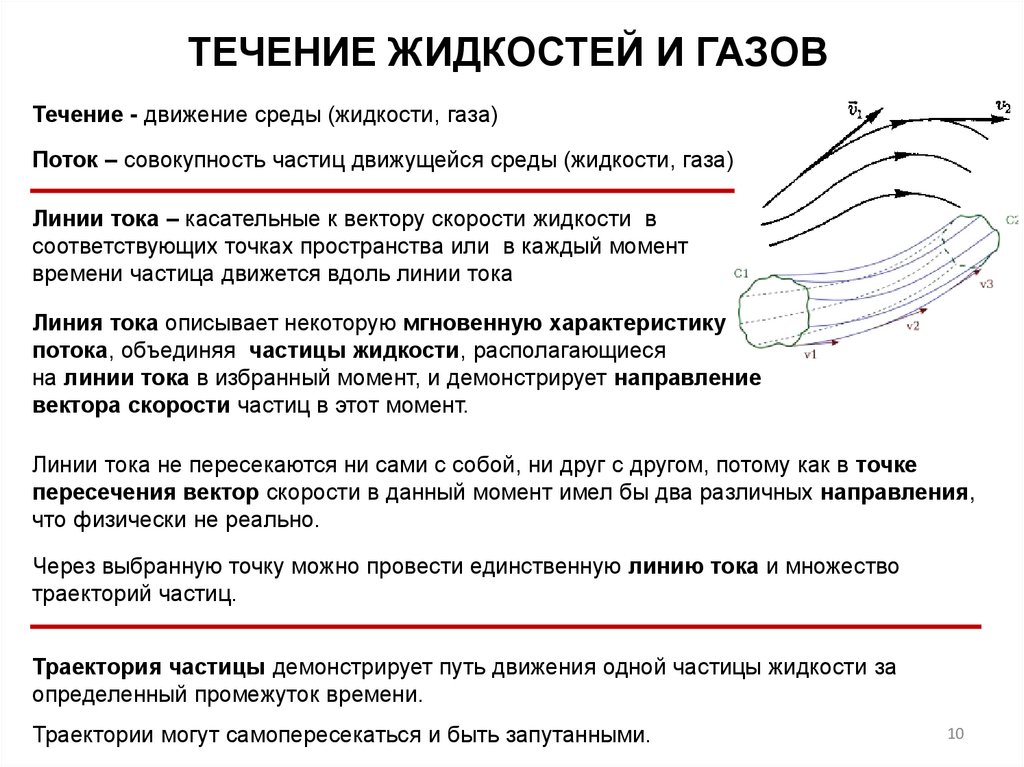
ТЕЧЕНИЕ ЖИДКОСТЕЙ И ГАЗОВ
Течение - движение среды (жидкости, газа)
Поток – совокупность частиц движущейся среды (жидкости, газа)
Линии тока – касательные к вектору скорости жидкости в
соответствующих точках пространства или в каждый момент
времени частица движется вдоль линии тока
Линия тока описывает некоторую мгновенную характеристику
потока, объединяя частицы жидкости, располагающиеся
на линии тока в избранный момент, и демонстрирует направление
вектора скорости частиц в этот момент.
Линии тока не пересекаются ни сами с собой, ни друг с другом, потому как в точке
пересечения вектор скорости в данный момент имел бы два различных направления,
что физически не реально.
Через выбранную точку можно провести единственную линию тока и множество
траекторий частиц.
Траектория частицы демонстрирует путь движения одной частицы жидкости за
определенный промежуток времени.
Траектории могут самопересекаться и быть запутанными.
10

11.

РЕЖИМЫ ТЕЧЕНИЯ ЖИДКОСТЕЙ И ГАЗОВ
Режим течения - условия массопереноса при течении среды
Установившееся (стационарное) - течение, при котором в каждой точке данного
объема скорость частиц жидкости не изменяется со временем. Частицы движутся вдоль
линий, сохраняющих свое положение в пространстве неизменным
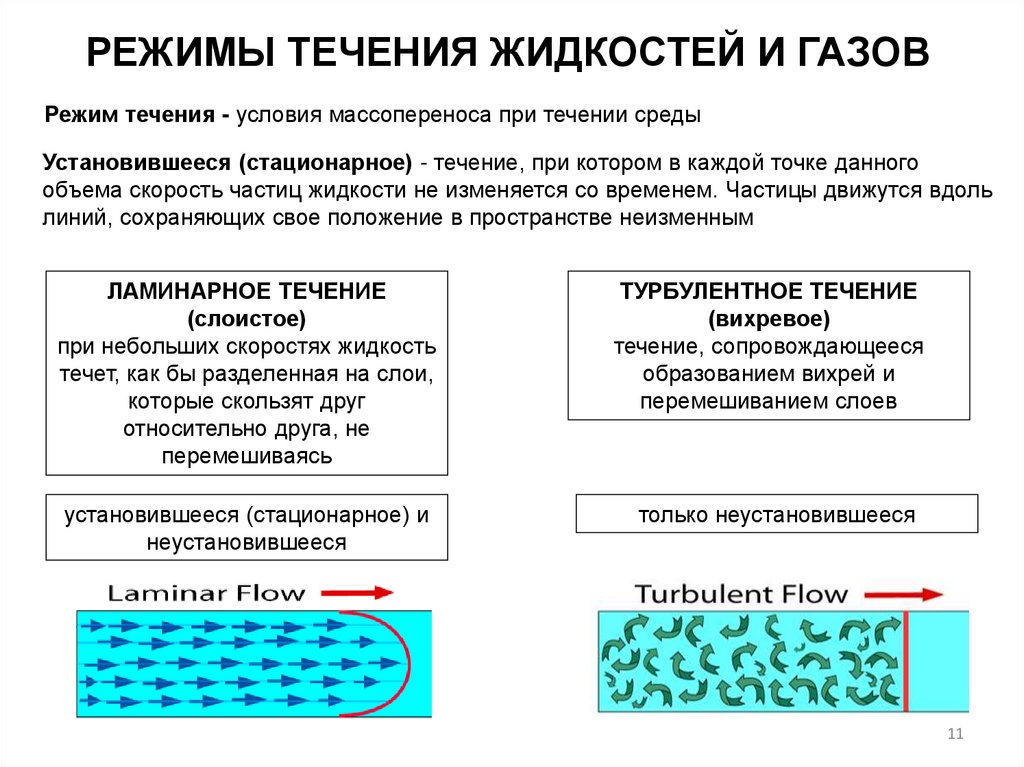
ЛАМИНАРНОЕ ТЕЧЕНИЕ
(слоистое)
при небольших скоростях жидкость
течет, как бы разделенная на слои,
которые скользят друг
относительно друга, не
перемешиваясь
ТУРБУЛЕНТНОЕ ТЕЧЕНИЕ
(вихревое)
течение, сопровождающееся
образованием вихрей и
перемешиванием слоев
установившееся (стационарное) и
неустановившееся
только неустановившееся
11

12.

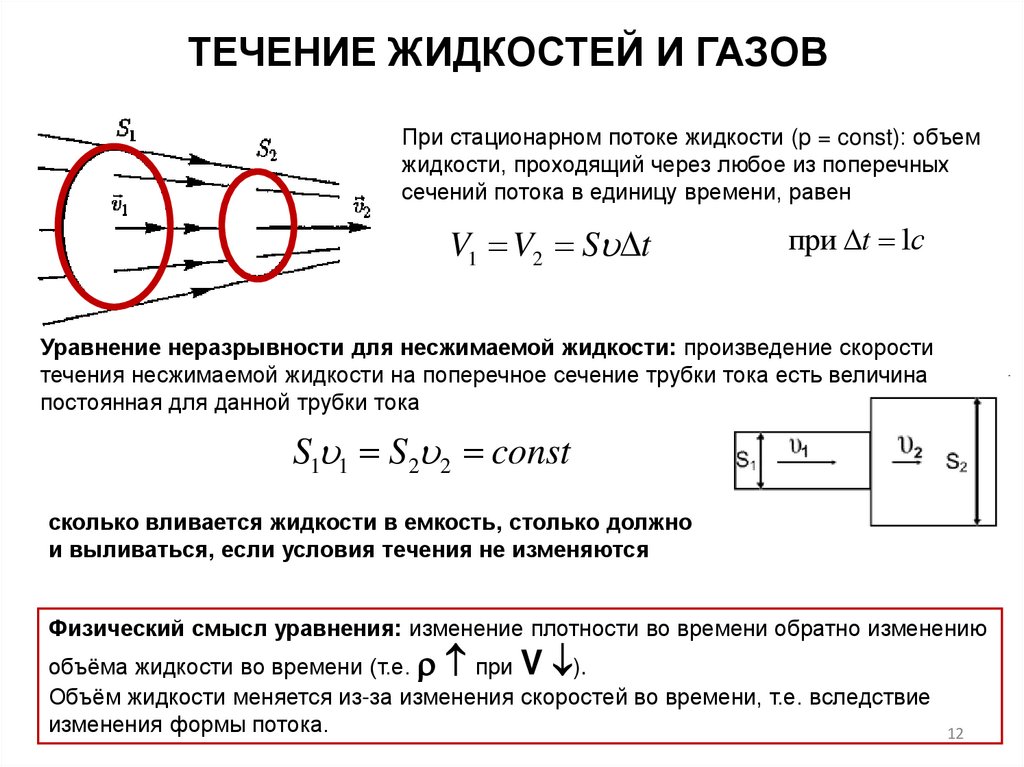
ТЕЧЕНИЕ ЖИДКОСТЕЙ И ГАЗОВ
При стационарном потоке жидкости (p = const): объем
жидкости, проходящий через любое из поперечных
сечений потока в единицу времени, равен
V1 V2 S t
при t 1с
Уравнение неразрывности для несжимаемой жидкости: произведение скорости
течения несжимаемой жидкости на поперечное сечение трубки тока есть величина
постоянная для данной трубки тока
S1 1 S2 2 const
сколько вливается жидкости в емкость, столько должно
и выливаться, если условия течения не изменяются
Физический смысл уравнения: изменение плотности во времени обратно изменению
объёма жидкости во времени (т.е. при V ).
Объём жидкости меняется из-за изменения скоростей во времени, т.е. вследствие
изменения формы потока.
12

13.

УРАВНЕНИЕ БЕРНУЛЛИ
( для идеальной жидкости)
Идеальная жидкость ─ это несжимаемая жидкость лишена
вязкости и теплопроводности при ее движении не происходит
превращения механической энергии во внутреннюю, поэтому
выполняется закон сохранения механической энергии:
Е2 Е1 А F1l1 F2l2
Даниил Бернулли
швейцарский физик
(1700 - 1782)
F1 p1 S1
F2 p2 S2 направлена в сторону, противоположно течению жидкости
m 12
E1
mgh1
2
m 22
E2
mgh2
2
S1 1 S2 2 const
уравнение неразрывности для несжимаемой
жидкости (V=const)
13

14.

УРАВНЕНИЕ БЕРНУЛЛИ
( для идеальной жидкости)
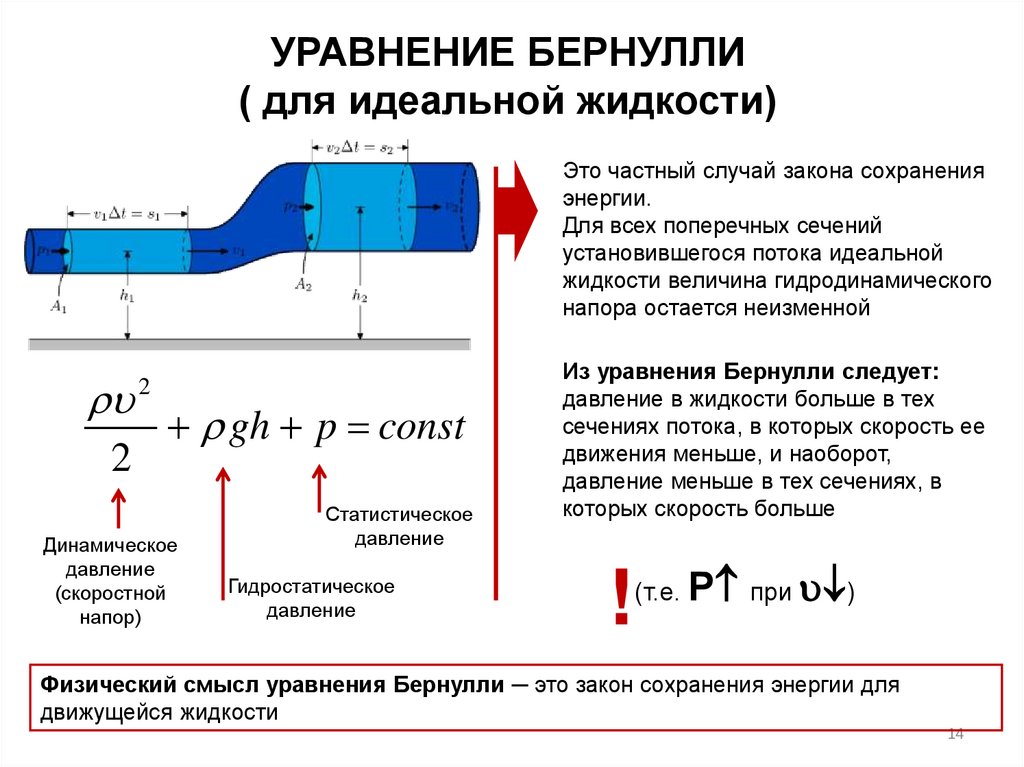
Это частный случай закона сохранения
энергии.
Для всех поперечных сечений
установившегося потока идеальной
жидкости величина гидродинамического
напора остается неизменной
2
2
gh p const
Динамическое
давление
(скоростной
напор)
Статистическое
давление
Гидростатическое
давление
Из уравнения Бернулли следует:
давление в жидкости больше в тех
сечениях потока, в которых скорость ее
движения меньше, и наоборот,
давление меньше в тех сечениях, в
которых скорость больше
!
(т.е. Р при )
Физический смысл уравнения Бернулли ─ это закон сохранения энергии для
движущейся жидкости
14

15.

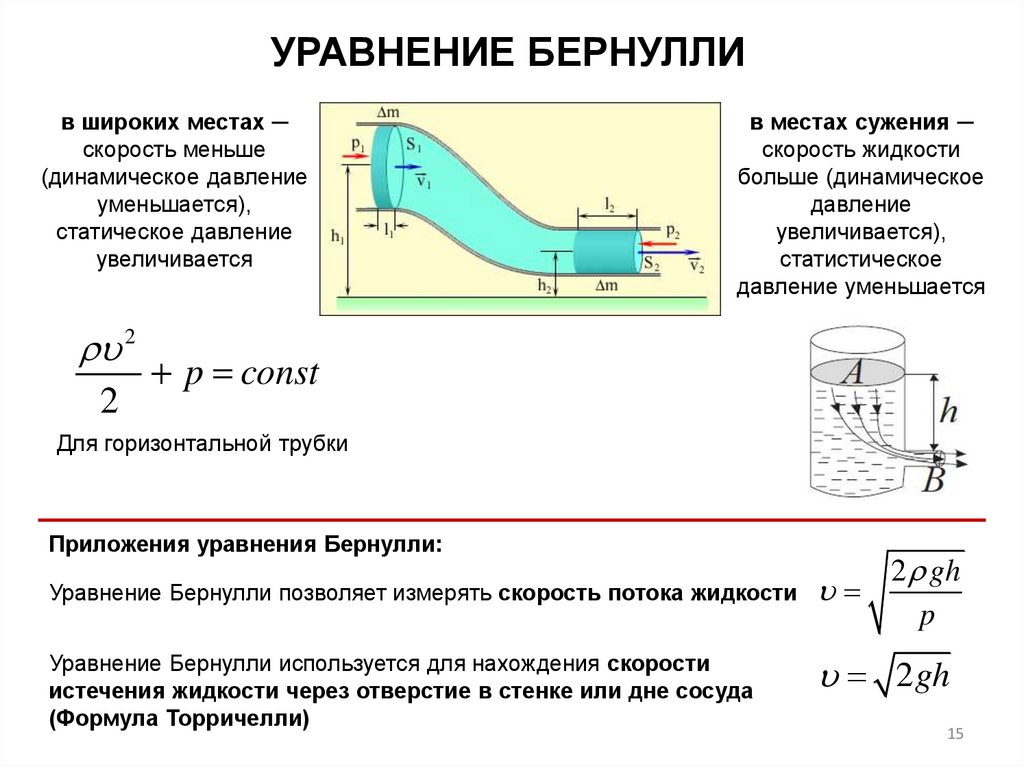
УРАВНЕНИЕ БЕРНУЛЛИ
в широких местах ─
скорость меньше
(динамическое давление
уменьшается),
статическое давление
увеличивается
2
2
в местах сужения ─
скорость жидкости
больше (динамическое
давление
увеличивается),
статистическое
давление уменьшается
p const
Для горизонтальной трубки
Приложения уравнения Бернулли:
Уравнение Бернулли позволяет измерять скорость потока жидкости
Уравнение Бернулли используется для нахождения скорости
истечения жидкости через отверстие в стенке или дне сосуда
(Формула Торричелли)
2 gh
p
2gh
15

16.

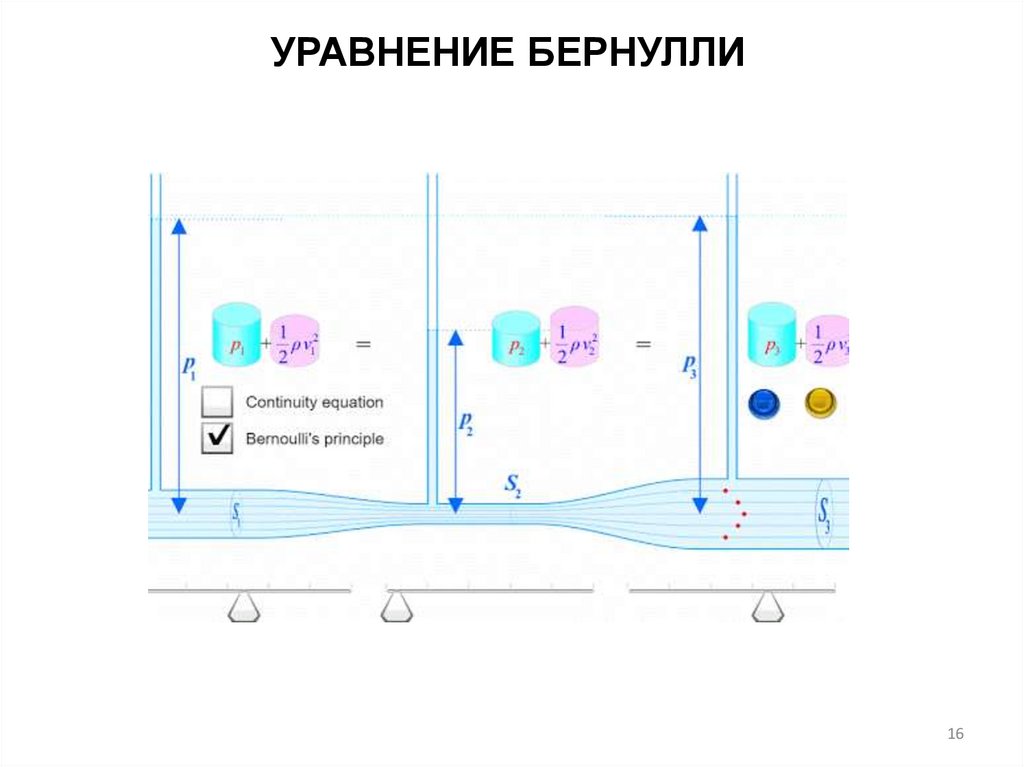
УРАВНЕНИЕ БЕРНУЛЛИ
16

17.

УРАВНЕНИЕ БЕРНУЛЛИ
В дне цилиндрического сосуда диаметром 0,5 м имеется круглое отверстие диаметром
1 см. Найти зависимость скорости понижения уровня воды в сосуде от высоты этого
уровня. Найти значение этой скорости для высоты 0,2 м.
12
h1
2
h0
gh1 p
22
2
h2 =0 т.к. отверстие находится на дне сосуда
12
2
2gh1
S1 1 S2 2
2
1
2
2
gh2 p
2 gh1
2
1
S1
D2
12 S12
S22
gh1
22
2
d 2 2 gh1
4
1
8
10
м/с
2
D
4
d2
S2
4
d 4 D4
17

18.

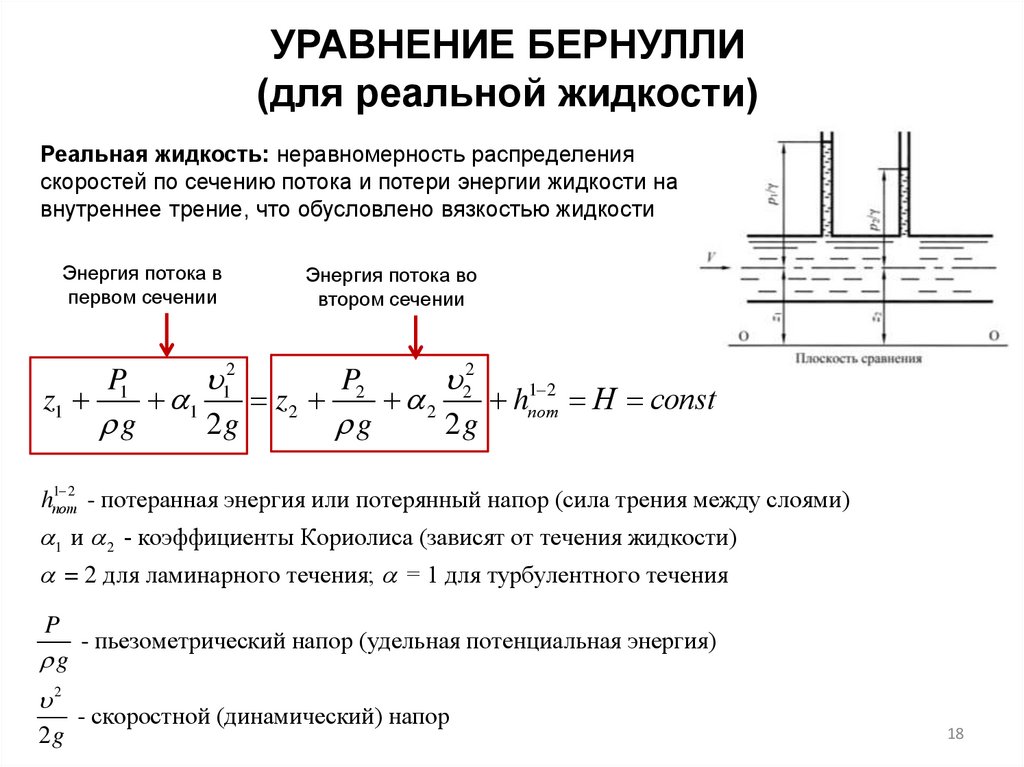
УРАВНЕНИЕ БЕРНУЛЛИ
(для реальной жидкости)
Реальная жидкость: неравномерность распределения
скоростей по сечению потока и потери энергии жидкости на
внутреннее трение, что обусловлено вязкостью жидкости
Энергия потока в
первом сечении
Энергия потока во
втором сечении
P1
12
P2
22
1 2
z1
1
z2
2
hпот
Н const
g
2g
g
2g
1 2
hпот
- потеранная энергия или потерянный напор (сила трения между слоями)
1 и 2 - коэффициенты Кориолиса (зависят от течения жидкости)
= 2 для ламинарного течения; = 1 для турбулентного течения
P
- пьезометрический напор (удельная потенциальная энергия)
g
2
2g
- скоростной (динамический) напор
18