Лекция 2 - НАУ

1.

2.

Нелинейное алгебраическое уравнение – уравнение вида
f(x) = 0
где f(x) – нелинейная функция.
Решить уравнение – найти все его корни или доказать, что их нет.
Этапы численного решения:
1. Отделение корней;
2. Уточнение корней.
Способы отделения корней:
- определение начальных интервалов локализации;
- определение начальных приближений.
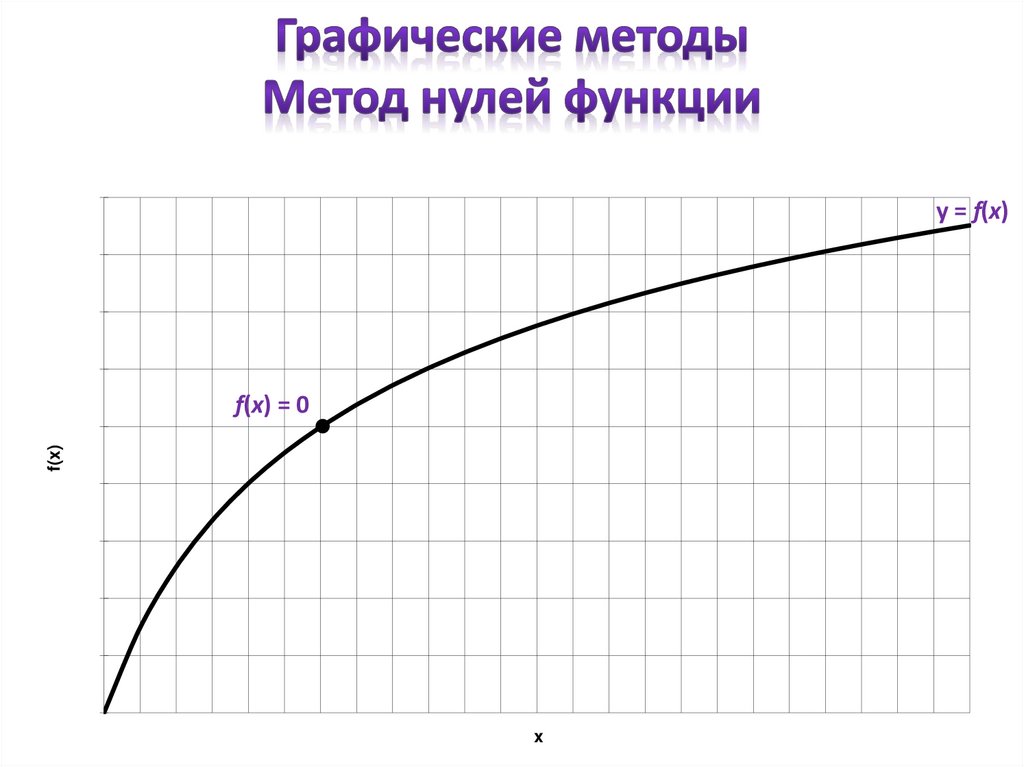
Для отделения корней используются графические методы:
- метод нулей функции;
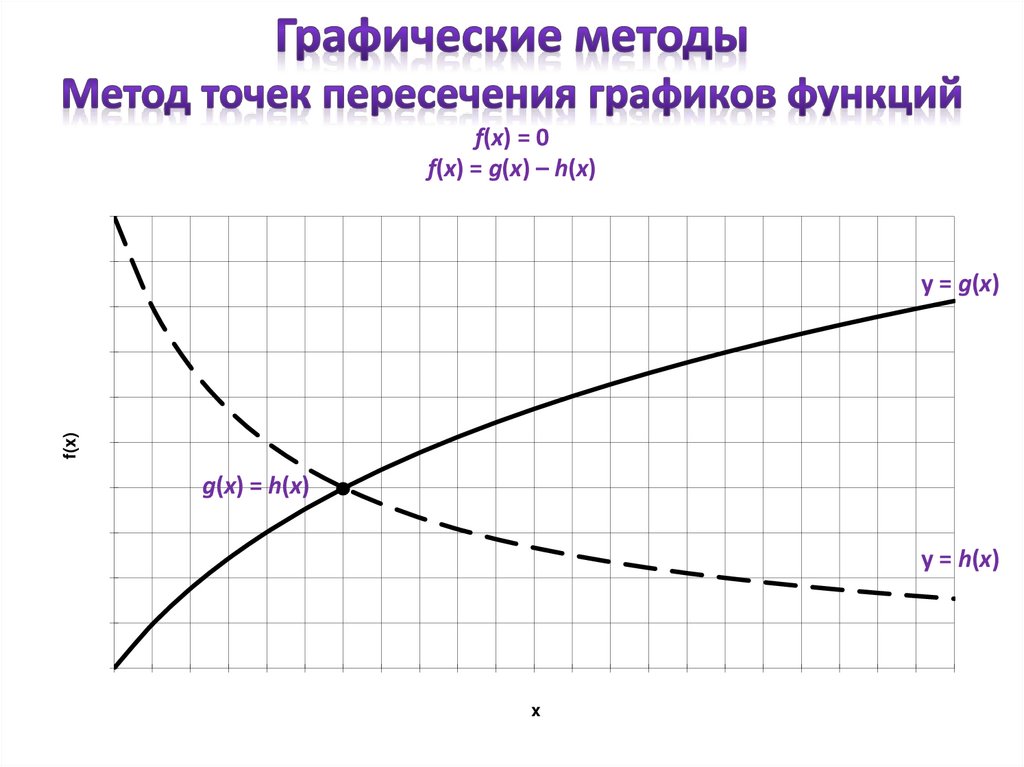
- метод точек пересечения графиков функций.

3.

y = f(x)
f(x)
f(x) = 0
x

4.

f(x) = 0
f(x) = g(x) – h(x)
f(x)
y = g(x)
g(x) = h(x)
y = h(x)
x

5.

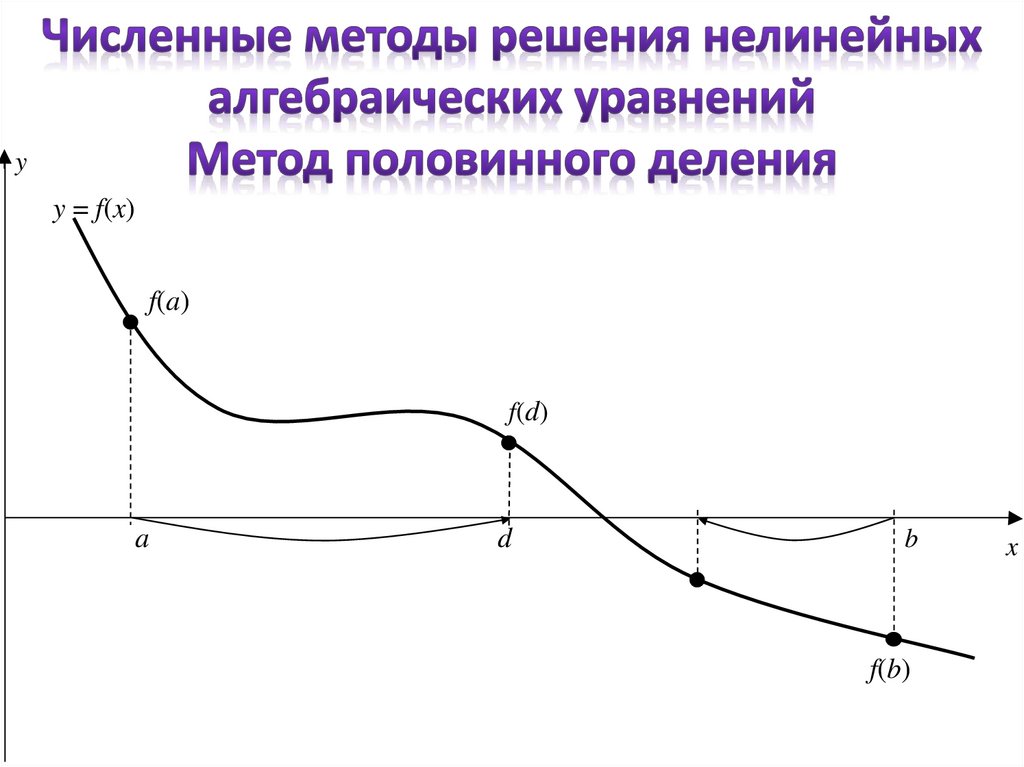
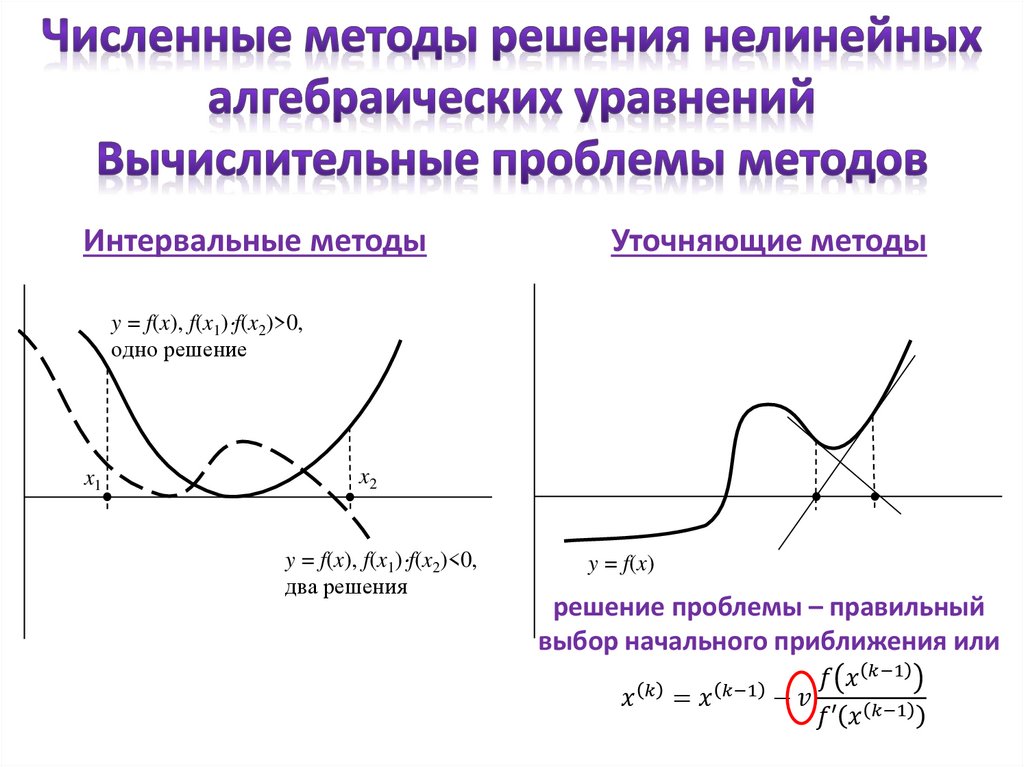
Интервальные методы:
- метод половинного деления;
- метод пропорциональных частей (хорд, секущих).
Для решения требуется задать:
- начальный интервал локализации решения [a, b];
- точность e.
Методы уточнения решения:
- метод простых итераций;
- метод Ньютона (касательных).
Для решения требуется задать:
- начальное приближение x0;
- точность e.

6.

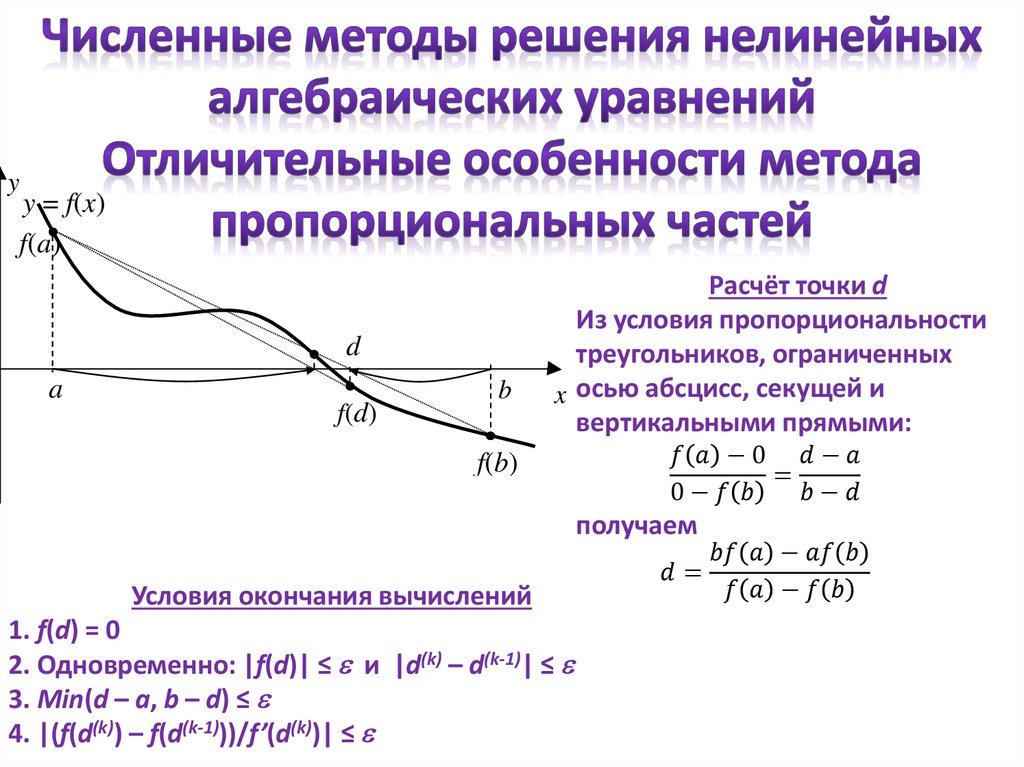
y
y = f(x)
f(a)
f(d)
a
d
b
f(b)
x

7.

y
y = f(x)
f(a)
f(d)
a
d
b
f(b)
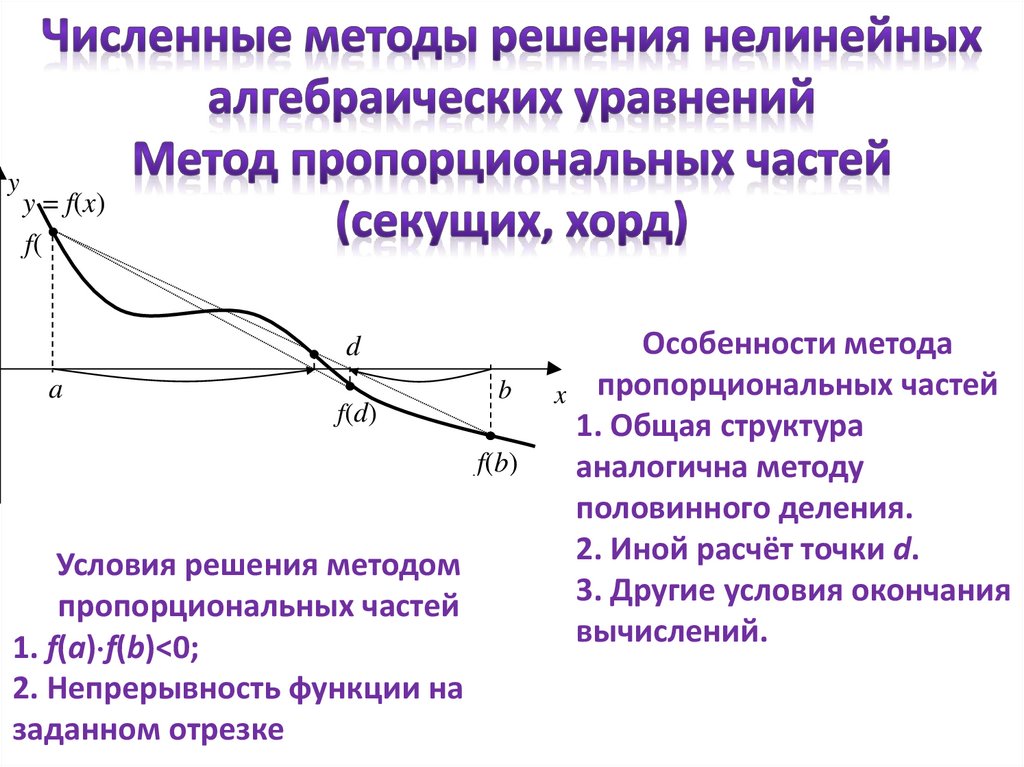
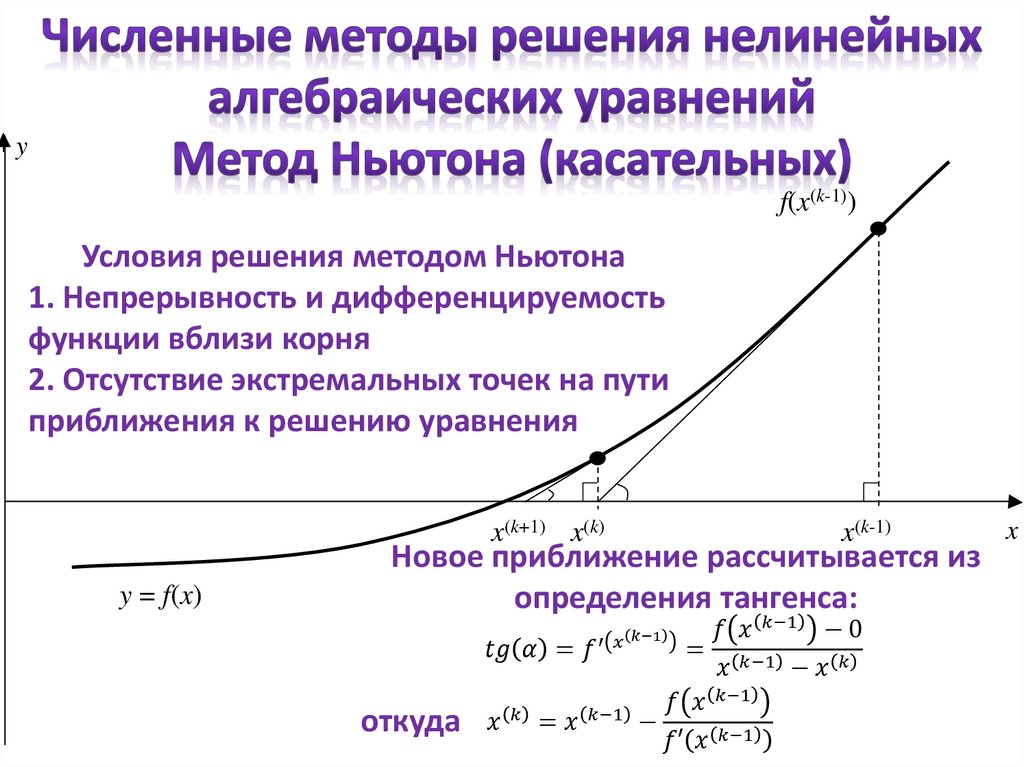
Условия решения методом
половинного деления
1. f(a) f(b)<0;
2. Непрерывность функции на
заданном отрезке
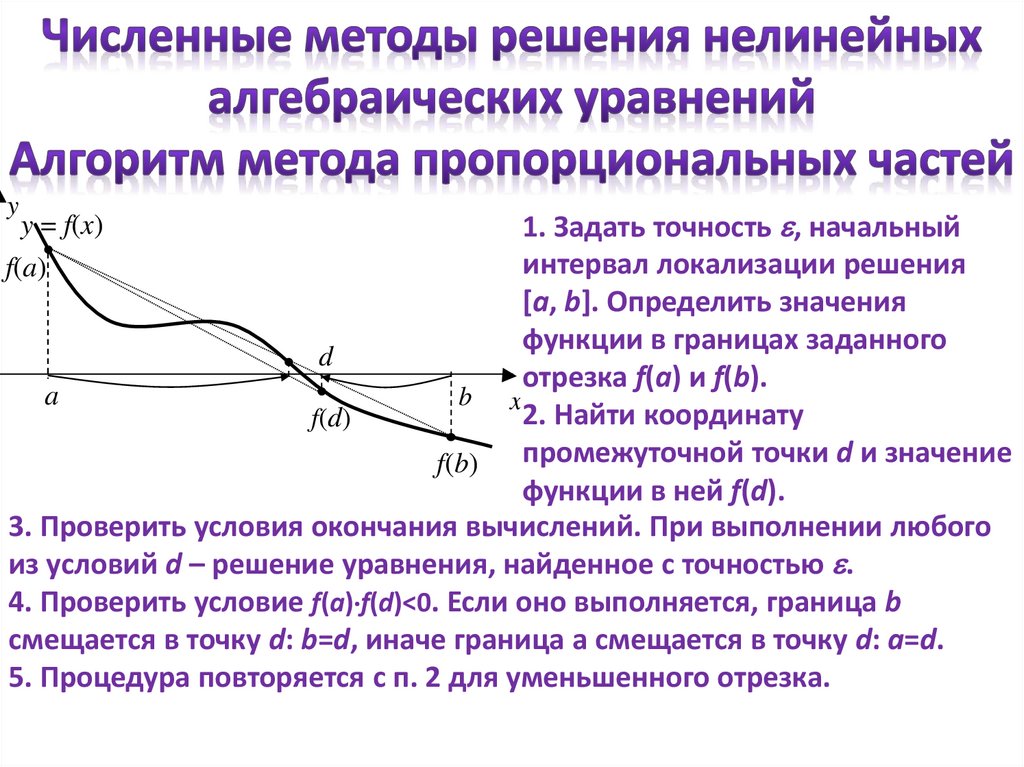
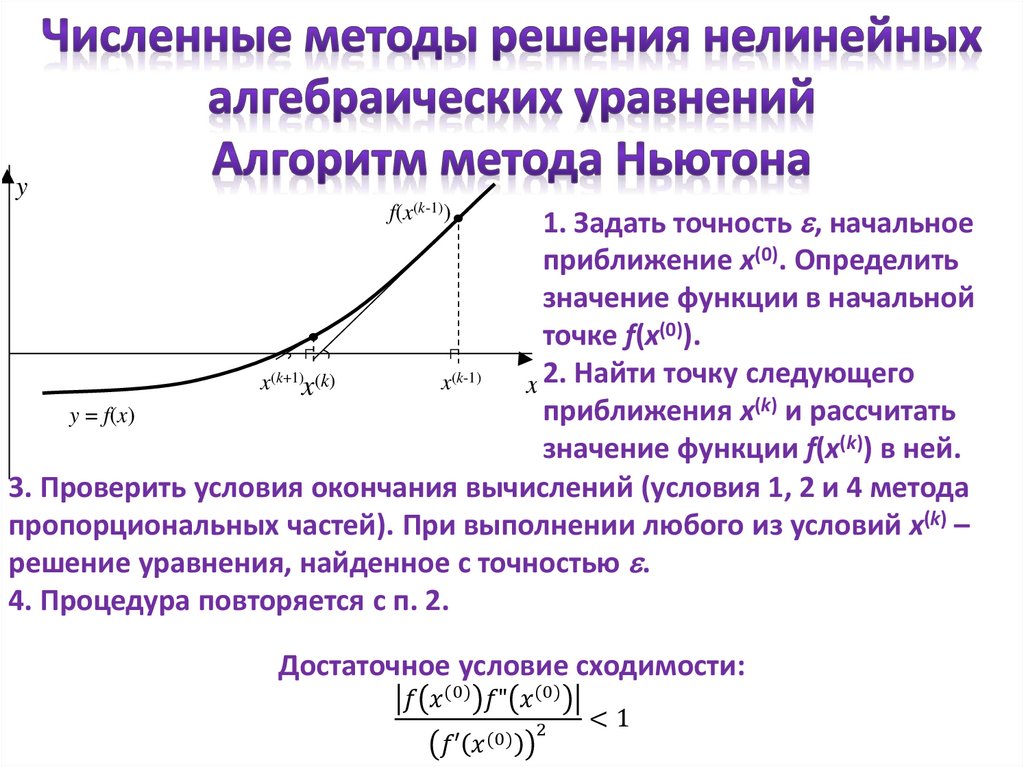
1. Задать точность e, начальный
интервал локализации решения
[a, b]. Определить значение
функции в левой границе
заданного отрезка f(a).
x
2. Найти координату середины
текущего отрезка d=(a+b)/2 и
значение функции в ней: f(d).
3. Проверить условия окончания
вычислений:
f(d)=0,
(b – a)/2≤e.
При выполнении любого из
условий d – решение уравнения,
найденное с точностью e.

8.

y
y = f(x)
f(a)
f(d)
a
d
b
f(b)
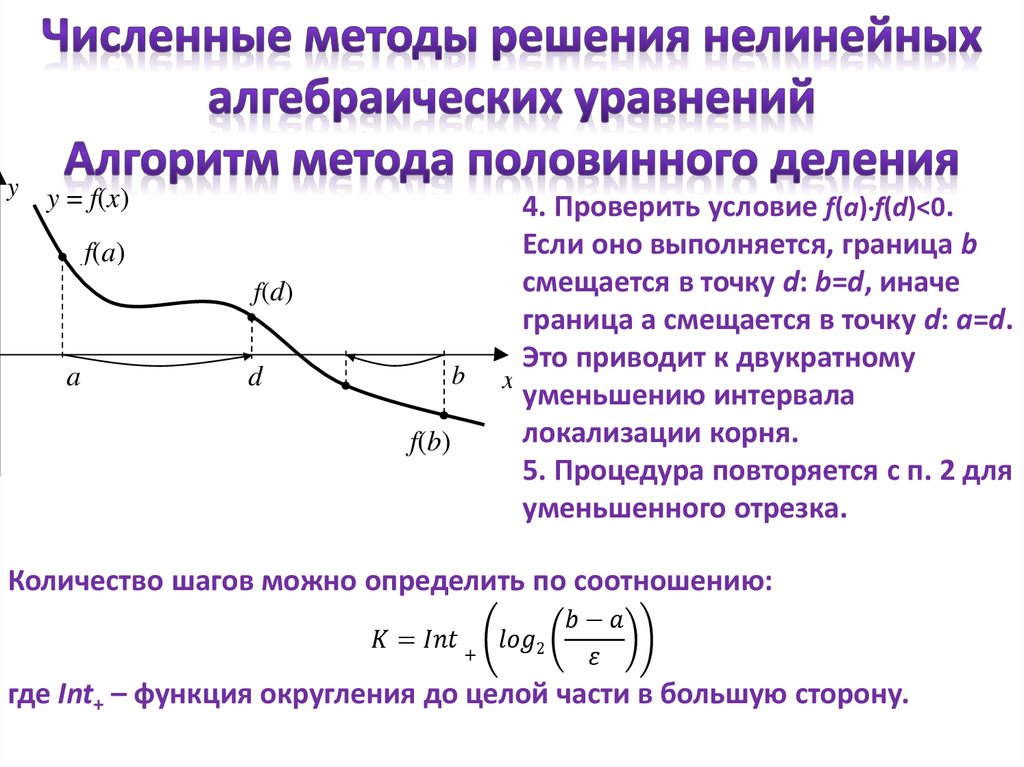
4. Проверить условие f(a) f(d)<0.
Если оно выполняется, граница b
смещается в точку d: b=d, иначе
граница a смещается в точку d: a=d.
Это приводит к двукратному
x
уменьшению интервала
локализации корня.
5. Процедура повторяется с п. 2 для
уменьшенного отрезка.
Количество шагов можно определить по соотношению: