1.1. Множества и операции над ними (2)

1.

§1. Множества
и операции над ними
п.1. Понятие множества.
Множество — одно из важнейших
математических понятий.
Георг Кантор (1845─1918):
Множество — совокупность каких-либо
различных предметов, объединенных в единое
целое.
Предметы, из которых составлено множество
будем называть элементами этого множества.

2.

Примеры множеств.
1) Множество студентов одной группы.
2) Множество теорем геометрии.
3) Множество корней какого-либо уравнения.
Обозначение:
множества А, В, С, …;
элементы множества а, b, с, …
x является элементом множества A
x A.

3.

Способы задания множества
1) С помощью перечисления элементов.
A {x1 , x2 ,..., xn }.
2) С помощью характеристического свойства.
A {x : x 3x 2 0}.
2
Множество, не содержащее ни одного
элемента, называется пустым.
Множество, содержащее все возможные
элементы, называется универсальным.
U

4.

Множество A называется подмножеством
множества В, если каждый элемент множества
A принадлежит множеству B.
A B.
A A;
A;
если A B и B C , то A C.
Множества A и В называются равными, если
A B и B A.
A B

5.

Операции над множествами
1) Пересечение (произведение) множеств.
Множество C называется пересечением
множеств A и B, если оно составлено из всех
элементов, которые одновременно
принадлежат множествам A и B.
Обозначение C A B.
Пример.
[2,5] (3,7) (3,5].

6.

2) Объединение (сумма) множеств.
Множество C называется объединением
множеств A и B, если оно составлено из всех
элементов, которые принадлежат хотя бы
одному из множеств A или B.
Обозначение C A B.
Пример.
[2,5] (3,7) [2,7).

7.

3) Разность множеств.
Множество C называется разностью множеств
A и B, если оно составлено из всех элементов,
которые принадлежат множеству A и не
принадлежат множеству B.
Обозначение C A \ B.
Пример.
[2,5] \ (3,7) [ 2,3].

8.

4) Дополнение множества.
Множество C называется дополнением
множества A, если оно составлено из всех
элементов, которые не принадлежат
множеству A.
Обозначение
Пример.
C A.
A [ 2,5].
A ( ,2) (5, ).

9.

5) Симметрическая разность.
Множество C называется симметрической
разностью множеств A и B, если оно
составлено из всех элементов, которые
принадлежат множеству A и не принадлежат
множеству B, а также из всех элементов,
которые принадлежат множеству B и не
принадлежат множеству A.
Обозначение C A B.
Пример.
A B ( A \ B ) ( B \ A).
[2,5] (3,7) [2,3] (5,7).
A B ( A B ) \ ( A B ).

10.

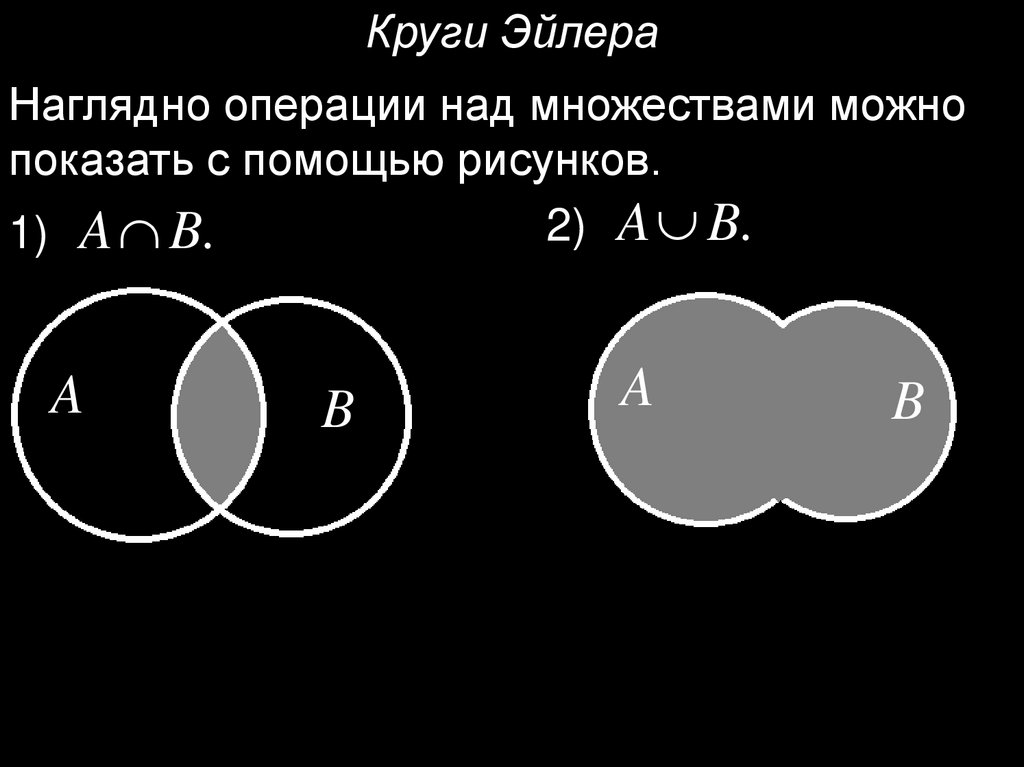
Круги Эйлера
Наглядно операции над множествами можно
показать с помощью рисунков.
2) A B.
1) A B.
A
B
A
B

11.

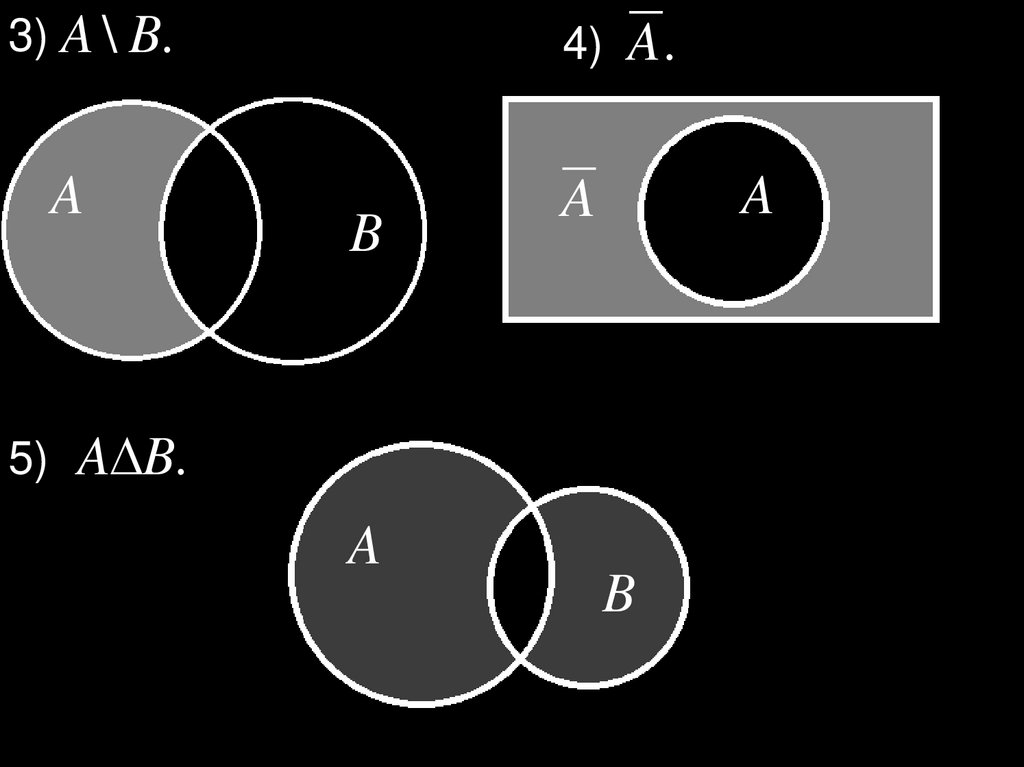
3) A \ B.
A
4) A .
B
A
A
5) A B.
A
B

12.

Свойства операций над множествами
A B B A, A B B A;
( A B) C A C B C;
( A B ) C A ( B C );
( A B ) C A ( B C );
A A A, A A A;
A U U , A U A;
A A U , A A ;
U , U , A A;
A B A B;
— законы де Моргана.
A B A B.

13.

п.2. Числовые множества.
Множества, элементами которых являются
числа, называются числовыми.
N {1,2,3,..., n,...}— множество натуральных
чисел.
x 5 2
Z {..., n,... 2, 1,0,1,2,..., n,...}
— множество целых чисел.

14.

2x 5
m
Q : m Z, n N
n
— множество рациональных чисел чисел.
Замечание 1.
Любое рациональное число можно
представить в виде бесконечной
периодической десятичной дроби.
Любая бесконечная периодическая
десятичная дробь является рациональным
числом.

15.

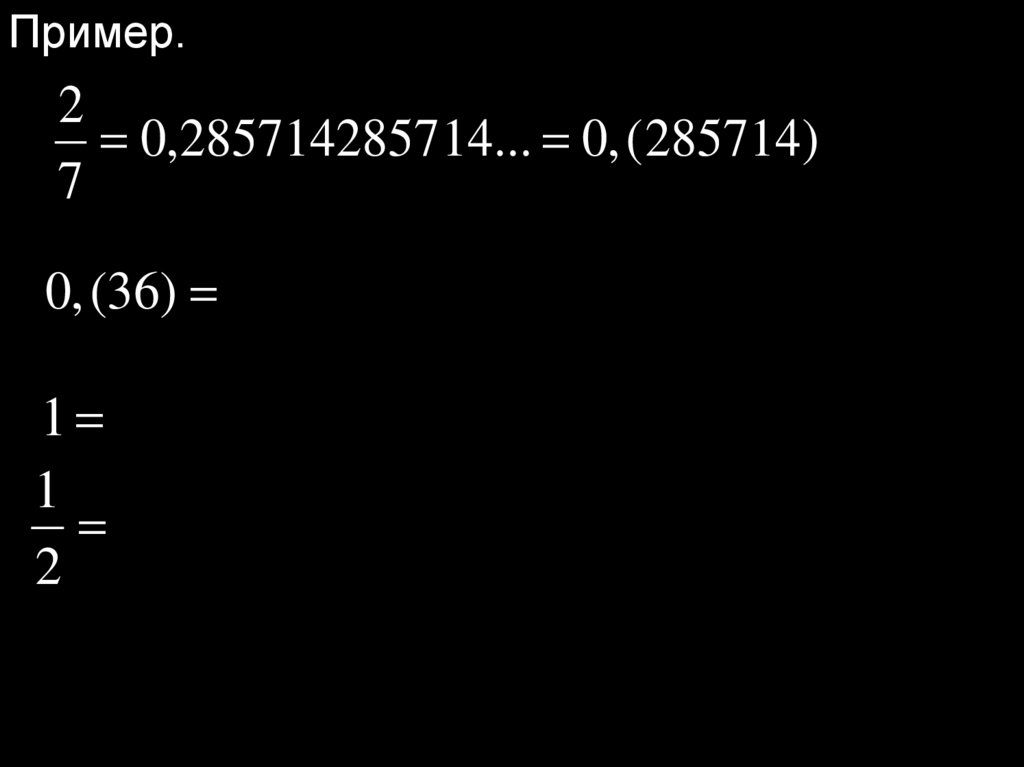
Пример.
2
0,285714285714... 0, (285714)
7
4
0, (36)
11
1
1
2

16.

x 5
2
Числа, которые можно представить в виде
бесконечной непериодической десятичной
дроби, называются иррациональными.
I
Множество, содержащее все рациональные и
иррациональные числа, называется
множеством действительных (вещественных)
чисел.
R

17.

Замечание 2.
Любому действительному числу соответствует
единственная точка на числовой прямой.
Каждой точке числовой соответствует
единственное действительное число.
0
Замечание 3.
N Z Q R
Q I R
1