Similar presentations:
Множества. Операции над ними. Комбинаторика
1.
БГТУ им. В.Г. ШуховаКафедра информационных технологий
Дискретная
математика
Коломыцева Елена Павловна, 2020
2.
Тема 1Множества
3.
МножестваПонятие множества относится к неопределяемым понятиям.
Множество состоит из некоторых объектов различных и
различаемых, которые называются элементами множества.
Например:
N- Множество натуральных чисел.
N 0 - множество натуральных чисел и 0.
Z- Множество целых чисел.
Q - Множество рациональных чисел. Множество Q так же можно
представить в виде множества дробей
p
, где p и q – целые числа.
q
R- Множество действительных чисел.
Одинаковые элементы, входящие во множество, не различаются и
считаются один раз.
Порядок элементов во множестве не определен.
Множество, не содержащее ни одного элемента, называется
пустым - Ǿ.
Способы задания множества:
1) Перечислением всех элементов множества. А={3,1,2,5}.
2) С помощью характеристического свойства.
В={x R/ (x+3)<4} или
В={x (-∞;1)}.
3) Процедурой. A={x2 /x N}
4.
ПодмножестваПусть задано множество А. Множество В, состоящее из элементов
множества А, называется подмножеством А.
Например. А={a, w, b, c} и В={w, a,b}, тогда В А или А В (В
включается в А или А включается в В).
Множество А является собственным подмножеством.
Множество, не содержащее ни одного элемента, называется
пустым Ø.
Пустое множество является подмножеством любого множества.
5.
Равенство множествДва множества называются равными, если они состоят из одних и
тех же элементов.
А={3, 2, а}. В={а, 3, а, 3, 2, а}. Имеем А=В.
Теорема. Множество А ровняется множеству В, если А является
подмножеством В, а В является подмножеством А.
Доказательство:
1) Пусть х А и А В. По определению подмножества х В.
Так как х- произвольный элемент А, то все элементы множества А
множеству В.
2) Пусть х В и В А. По определению подмножества х А.
Так как х- произвольный элемент В, то все элементы множества В
множеству А.
3) Так как все элементы множества А множеству В, а все
элементы множества В множеству А, то по определению равенства
множеств А=В.
Что и требовалось доказать.
Все множества рассматриваются как подмножества некоторого
универсального множества U.
6.
Мощность множествКоличество элементов, входящих во множество, называется его
мощностью.
Для бесконечных множеств говорить о количестве элементов не
имеет смысла, но говорить о мощности множества можно.
Два множества называются равномощными, если существует метод,
позволяющий каждому элементу одного множества поставить в
соответствие элемент другого множества.
Пример:
Имеется множество натуральных чисел и имеется множество четных
чисел. Равномощны ли они?
Ответ: Да.
1 2 3 4 5…
↓ ↓ ↓ ↓ ↓
2 4 6 8 10…
Множества, равномощные множеству натуральных чисел,
называются счетными.
7.
Алгебра множеств. Операции над множествами.Условимся U изображать в виде прямоугольника
а множество А-
(круги Эйлера-Венна)
А
Рис.1. Множества А и U.
8.
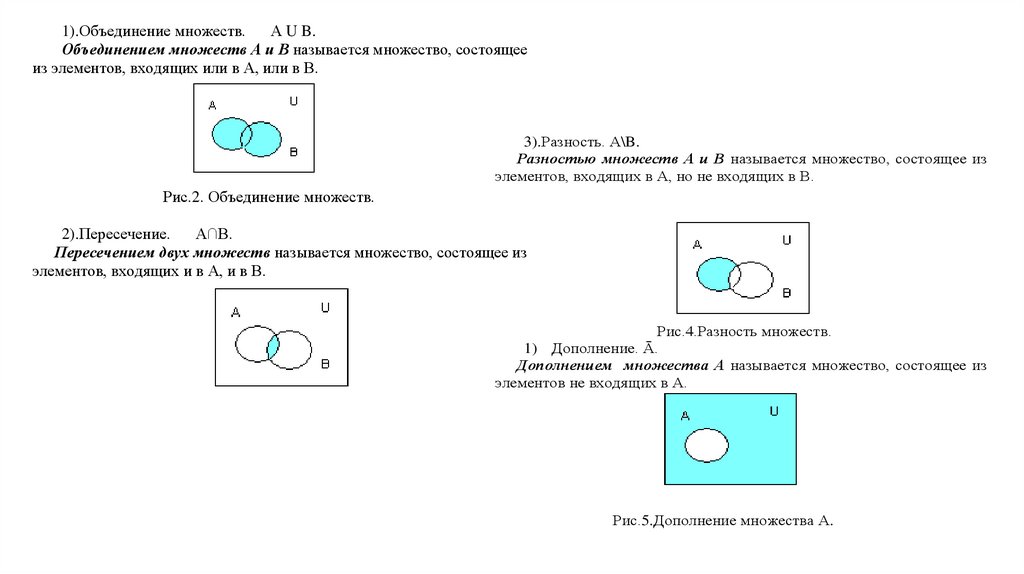
1).Объединение множеств.А U B.
Объединением множеств А и В называется множество, состоящее
из элементов, входящих или в А, или в В.
3).Разность. А\B.
Разностью множеств А и В называется множество, состоящее из
элементов, входящих в А, но не входящих в В.
Рис.2. Объединение множеств.
2).Пересечение.
А∩В.
Пересечением двух множеств называется множество, состоящее из
элементов, входящих и в А, и в В.
Рис.4.Разность множеств.
1) Дополнение. Ā.
Дополнением множества А называется множество, состоящее из
элементов не входящих в А.
Рис.5.Дополнение множества А.
9.
5.Симметрическая разность A ∆ B.Симметрической разностью множеств А и В называется
множество, состоящее из тех элементов множества А, которые не
принадлежат множеству В и тех элементов множества В, которые
не принадлежат множеству А.
Рис.4.Симметрическая разность множеств.
10.
Включение множествМножество А, все элементы которого принадлежат множеству В,
называется подмножеством множества В.
Обозначение. Нестрогое включение обозначается
, означает,
что А - несобственное подмножество множества В, возможно
совпадающее с В. Строгое включение обозначается
, и означает,
что А - подмножество множества В, не совпадающее с
B.
читается "А включено в В".
Отличия
и
заключается
в
том,
что
отношение
допускает и тождественность (А=В), т.е. любое
множество можно рассматривать как подмножество самого
себя
,
в
то
время
как
символ строгого
включения
ставится тогда, когда мы хотим подчеркнуть,
что
, то есть во множестве В содержатся не только элементы
множества А. Выполнение соотношений
и
возможно
только при А=В. И обратно, А=В, если
и
. Эти
соотношения являются признаком равенства множеств через
отношение включения. Заметим, что иногда в литературе
символом ⊂ обозначают "нестрогое" включение, допускающее и
равенство множеств. В этом случае символ ⊆ не используется, а
строгое
включение
записывают
двумя
соотношениями
,
.
11.
Свойства операций1)
2)
3)
4)
Коммутативность.
АUB=BUA.
A∩B=B∩A.
Ассоциативность.
АU(BUC)=(AUB)UC.
A∩ (B∩C) = (A∩B) ∩C.
Дистрибутивность.
А∩(BUC)=(A∩B)U(A∩C). AU (B∩C) = (AUB) ∩ (AUC).
Законы Де-Моргана.
A B= AUB
AUB = A ∩ B
5)
6)
7)
AUA=A A∩A=A
AUØ=A A∩Ø= Ø
A U=U A∩U=A
8)
A
A U
A A
10) A\B= В А
9)
A
A Ø
12.
Разбиение множества на классыПусть задано некоторое множество, например множество
треугольников. В этом множестве выделим свойство (например, быть
прямоугольным). Тогда множество разбивается на два класса:
прямоугольные и непрямоугольные.
Разбиение множества на классы (классификация) означает, что
данное множество А разбивается на подмножества k 1 , k 2 ,.., k m таких,
что
1) Эти подмножества попарно не пересекаются, то есть
k i k j Ø
(i, j=1,…m, i≠j)
2)
Объединение всех подмножеств дает множество А
m
k
i
A
i 1
3) Ни одно из подмножеств не пусто
ki ≠ Ø
13.
Пример: Пусть имеется А - множество всех грибов.Свойства:
1) 1 -быть съедобным грибом.
2) 2 -быть трубчатым грибом.
Таким образом, с помощью этих свойств мы получаем 4
подмножества:
съедобные и несъедобные
трубчатые и не трубчатые
Такое разбиение классификацией не является, так как эти
подмножества могут пересекаться, и пересечение не пусто.
Пусть В-множество съедобных грибов, а С - множество трубчатых.
k1 =B∩C-съедобные и трубчатые.
k 2 =B∩ С -съедобные и не трубчатые.
k 3 = В ∩C-несъедобные и трубчатые
k 4 = В ∩ С -несъедобные и не трубчатые.
14.
Декартово (прямое) произведение множества1 и а 2 . Пара ( а1 , а 2 ) называется
упорядоченной. 1-ый элемент ее - а1 , 2-ой- а 2 .
Пары ( а1 , а 2 ) и ( b1 , b2 ) считаются равными, если а1 = b1 , а а 2 = b2 ;
Пара ( а1 , а 2 )=( а 2 , а1 ), если только а1 = а 2 .
Пусть у нас имеется два элемента
Пример1
Пусть заданы два множества
А={ à1 , à 2 ,…, à n } и В={ b1 , b2 ,… bm }.
Декартовым или прямым произведением множества А на множество В
называется множество упорядоченных пар, 1-ый элемент которых принадлежит
множеству А , а 2-ой множеству В.
Обозначается декартово произведение знаком Х.
Для данных множеств получим
АхВ={( à1 , b1 ),( à1 , b2 ),…,( à1 , bm ),…,( a 2 , b1 ),…,( à n , bm )}
Мощность декартового произведения равна nm.
Обозначение: |A X B|=nm.
Пример:
A= {1, 4} и В {2, 3, 4}. A X B={(1,2),(1,3),(1,4),(4,2),(4,3),(4,4)}
Геометрически каждой паре чисел соответствует точка координатной плоскости.
Рис.8. Декартово произведение А Х В для конечных А и В.
15.
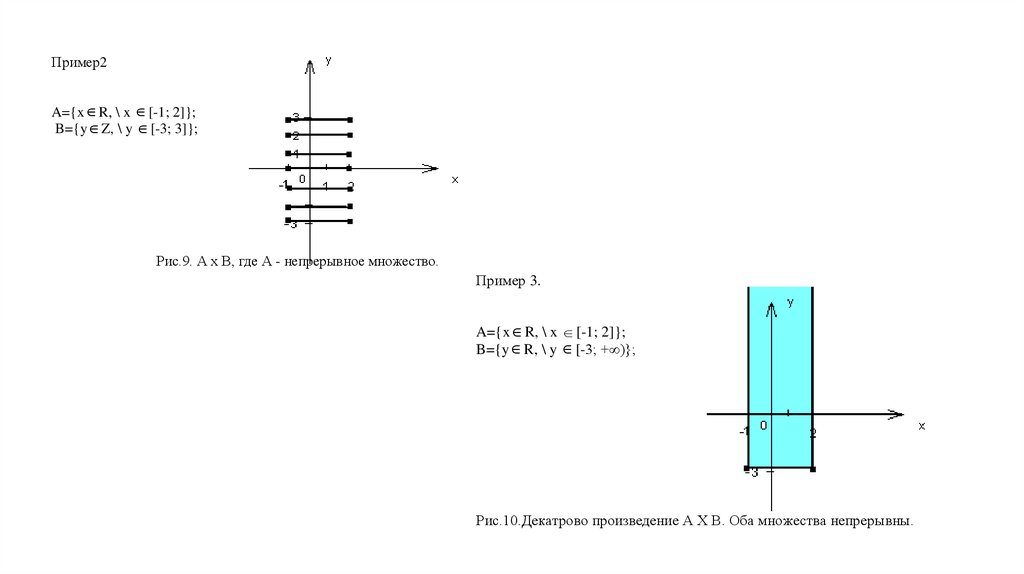
Пример2A={x R, \ x [-1; 2]};
B={y Z, \ y [-3; 3]};
Рис.9. А х В, где А - непрерывное множество.
Пример 3.
A={x R, \ x [-1; 2]};
B={y R, \ y [-3; +∞)};
Рис.10.Декатрово произведение А Х В. Оба множества непрерывны.
16.
Декартова степень.Если в качестве множества В в декартовом произведении выбрать множество А,
мы будем говорить о декартовом квадрате.
А Х А=А
2
2
А Х А =А
…
n 1
3
n
АХА
=А
Набор n-элементов будем зазывать кортежем.
Декартовым произведением n-множеств
А 1 х А 2 х А 3 х…х А n будем называть множество упорядоченных кортежей, 1ый элемент которых принадлежит множеству А 1 , 2-ой множеству А 2 и т.д.
17.
Свойства Декартового произведения.1)
2)
3)
4)
5)
6)
7)
8)
А Х В≠В Х А.
(А Х В) Х С≠А Х (В Х С).
А Х (В∩С)=(А Х В)∩(А Х С).
А Х (В С)=(А Х В) (А Х С).
(А∩В) Х С=(А Х С) ∩(В Х С).
(А В) Х С=(А Х С) (В Х С).
А Х (В\С)=(А Х В)\(А Х С).
(А\B) X C= (A X C)\ (B X C).
18.
Отношения.Пусть заданы два множества А и В. Найдем А Х В.
Подмножество k А Х В называется отношением из множества А во
множество В.
Отношения задаются знаками =, <, >, ,
и т.д.
Пример:
А={2,3,4}, B={1,4,3}
A X B={(2,1),(2,4),(2,3),(3,1),(3,4),(3,3),(4,1),(4,4),(4,3)}
Выделим отношения больше > k1 ={(2,1),(3,1),(4,1),(4,3)}
и меньше <
k 2 ={(2,4),(2,3),(3,4)}
Рис.11. Отношение >.
19.
Композиция отношений.Пусть отношение
k1 А Х С и отношение k 2 С Х В.
Композицией этих отношений является отношение k= k1 k 2 , где k A X B.
Композицией отношений из А в В называется множество пар (а,b) таких, что, а
А, b B и существует такое с С, что (а, с) k1 и (с,b) k 2 .
Пример:
А={2,3,4}, B={1,4,3}, С={2,5}
A X В={(2,1),(2,4),(2,3),(3,1),(3,4),(3,3),(4,1),(4,4),(4,3)}
A X C={(2,2),(2,5),(3,2),(3,5),(4,2),(4,5)}
C X B={(2,1),(5,1),(2,4),(5,4),(2,3),(5,3)}
Определим отношение
>: k1 A X C={(3,2),(4,2)} и отношение < k 2 C X B= {(2, 4), (2, 3)}
Возьмем пару (3,2) k1 . В k 2 есть пары, начинающиеся с 2. Это пары (2,4) и
(2,3). Значит пары (3, 4) и (3, 3) войдут в композицию k.
Берем пару (4,2) k1 . В k 2 есть пары, начинающиеся с 2. Это те же пары (2,4) и
(2,3). Значит пары (4, 4) и (4, 3) войдут в k.
Получим k= k1 k 2 =(k AXB)= {(3, 4), (3, 3), (4, 4), (4, 3)}
Таким образом, для элемента (2,4) А Х В, в k войдут {(2,х), (у,4)}, где (2,х)
k1 , а (у,4) k 2 для всех х и y.
20.
Отношения на множестве.Если в декартовом произведении в качестве множества В выбрать множество А (
2
2
то есть А Х А= А ), то отношение k из А называется отношением на множестве.
Для отношений на множестве вводятся понятия:
2
Обратное отношение-это множество пар (а,b) таких, что (b,a) А .
Обозначение
k
1
Дополнение-это множество пар (а,b) k. Обозначение k
Тождественное отношение-множество пар (а, а) таких, что, а А,
I= {(a, a), a A}
Универсальное отношение U={(a,b),a A, b А}
21.
Виды отношений1) Инъекция.
Если каждый элемент множества А соответствует элементу из множества В, то
отношение f называется инъективным.
Рис.12.Инъекция.
1) 3) Биекция.
Если для каждого элемента y B существует ровно один элемент х А, которому
соответствует y , то такое отношение называется биективным.
Биективное отношение инъективно и сюръективно.
Биективное отношение имеет обратное отношение.
2) Сюръекция.
Если для каждого элемента y множества В существует элемент х А,
соответствующий элементу y, то такое отношение f называется сюръекцией.
Рис.14. Биекция.
22.
Функции.Пусть заданы множества А и В. Найдем А Х В.
Выберем отношение f АХВ={( à1 , b1 ),( à 2 , b2 ),…}, состоящее из пар таких,
что
ài ≠ à j , i=1,2,3,…., то есть отношение, в которой все первые элементы пар
различны. Такие отношения называются функциями.
Способы задания:
B; b=f (a); a f b.
А В; f: A
Пример: А={2,3,4}, B={1,4,3}
A X В={(2,1),(2,4),(2,3),(3,1),(3,4),(3,3),(4,1),(4,4),(4,3)}
Выделим: функции f1 ={(2,1),(3,1),(4,1)} и f 2 ={(2,4),(3,1),(4,1)}
F
Рис.15.Функция
f1 .
Рис.16.Функция
f2.
23.
Тема 2Комбинаторика
24.
Комбинаторика.Задачи, в которых требуется определить количество возможных операций,
называется комбинаторными.
Пусть имеется группа некоторых объектов α1 , a 2 , a3 ,..., a m , которые мы будем
называть элементами.
Из этой группы элементов будем образовывать подгруппы. Такие подгруппы
будем называть соединениями.
Из этих соединений выделим классы, которые будем называть размещениями.
25.
Размещения.Размещениями из m-элементов по n называются соединения, каждое из которых
содержит n элементов, взятых из данных m и которые отличаются друг от друга или
элементами, или их порядком.
Предполагается, что элементы водном размещении не повторяются.
Формула числа размещений без повторений.
1
Размещения из m по одному. Очевидно, что их число: А m =m
Составим размещения по 2:
α1, a2 , a1a3 , a1a4 ,..., a1am
-размещений (m-1)
a 2 a1 , a 2 a 3 , a 2 a 4 ,..., a 2 a m
a a , a a , a a ,..., a a
3 1 3 2 3 4
3 m
m-строк
...................................
a m a1 , a m a 2 , a m a 3 ,..., a m a m 1
Итого:
2
А m =m(m-1)
26.
Размещения.Размещения по 3: В каждой строке будет (m-2) размещений
А2
m
a1 a 2 a 3 , a1 a 2 a 4 ,..., a1 a 2 a m
a a a , a a a ,..., a a a
1 3 2 1 3 4
1 3 m
-строк
...................................
a m a m 1 a1 , a m a m 1 a 2 ,..., a m a m 1 a m 2
Ясно, что
3
2
А m = А m (m-2)=m(m-1)(m-2)
4
А m = m(m-1)(m-2)(m-3)
………………………………
n
А m = m(m-1)(m-2)….(m-(n-1))
( *)
27.
Размещения.Пример:
В группе 21 студент. Требуется выбрать старосту, профорга и физорга. Сколькими
способами это можно сделать?
Решение:
Каждая тройка студентов может отличаться от другой тройки или распределением
обязанностей, или хотя бы одним из студентов, то есть мы должны вычислить число
размещений из 21 по 3:
m=21, n=3.
3
А 21 =21*20*19=7980.
28.
Размещения.Другой вид формулы числа размещений.
Умножим числитель и знаменатель формулы ( * ) на (m-n)! Получим
n
Аm
m * (m 1) * (m n 1) * (m n) * (m n 1).....2 * 1
=
, или
(m n) * (m n 1)....2 * 1
n
Аm
m!
=
(m n)!
Каждое размещение содержит одно и то же количество элементов, взятых из
данных m.
29.
Перестановки.Размещения из n-элементов по n, каждое из которых отличается друг от друга
только порядком элементов, называются перестановками.
Их число обозначается Pn :
Pn =А nn =n*(n-1)*(n-2)…..2*1, то есть
Pn =n!
Пример:
Сколькими способами могут сесть 6 человек на 6-местную лавочку?
Решение:
В данном случае каждое расположение лиц на лавочке отличается от другого
расположения только порядком. Поэтому мы имеем дело с перестановками:
P6 =6!=720.
30.
Сочетания.Сочетания - это размещения, каждое из которых отличается от других хотя бы
одним элементом.
Другими словами: Сочетания - это соединения, содержащие n элементов из
данных m, отличающиеся хотя бы одним элементом.
n
Число сочетаний С m . Если мы имеем m- элементов, и из них составим
всевозможные сочетания по n и внутри каждого произведем перестановку, то
получим размещения.
n
n
С m * Pn = А m отсюда
n
A
m!
n
m
Сm=
=
Pn ( m n)! n!
31.
Сочетания.Пример:
В группе 20 студентов. Требуется выбрать 5 делегатов на конференцию.
Сколькими способами это можно сделать?
Решение:
Так как внутри каждой пятерки делегатов перестановки дают одну и ту же
пятерку, то каждая пятерка должна отличаться от других хотя бы одним делегатом. В
данном случае мы должны посчитать число сочетаний из 20 по 5:
5
С 20 =
20!
=15504.
15!*5!
32.
Свойства сочетаний.1)
m n
n
С m =С m
, достаточно выписать формулы левой и правой части равенства.
0!
1 , т.к. по определению 0!=1
(0 0)!0!
1!
0
1 , т.к. по определению 1!=1
3) С 1 =
1!*0!
2)
0
С0=
k 1
k
k
4) С n = С n 1 + С n 1
Доказательство:
(n 1)!
(n 1)!
+
=
(k 1)! (n 1 (k 1))! k! (n 1 k )!
(n 1)!*k (n 1)!*(n k )
(n 1)!*(k n k )
( n 1)!*n
=
=
=
k!*(n k )!
k!*(n k )!
k!*(n k )!
n!
k
=Сn
k!*(n k )!
k 1
k
С n 1 +
С n 1 =
Что и требовалось доказать.
1)
k 1
k
Сn =Сn
*
(n k 1)
k
Доказательство:
n!*(k 1)! (n (k 1))! (n k 1)
k
k 1
=
, следовательно, С n = С n
к 1
k
k!*(n k )!*n!
Cn
(n k 1)
*
.
k
С nk
=
Что и требовалось доказать.
33.
Размещения с повторениями.До сих пор мы рассматривали комбинации элементов, которые в каждой
комбинации не повторялись. Рассмотрим размещения из m-элементов по n, в которых
каждый элемент может повторяться. Такие размещения называются размещениями
n
с повторениями: Ậ m .
Рассмотрим задачу.
В лифт 9 этажного дома на 1-ом этаже вошло 10 человек, каждый из которых
может выйти на любом этаже, начиная со второго. Сколькими способами они могут
выйти из лифта?
Решение:
Каждый из пассажиров может выйти 8 способами. Два пассажира могут выйти
2
2
10
Ậ 8 =8*8=8 =64. Десять человек могут выйти Ậ810 = 8 .
Таким образом, так как каждый элемент попадает в комбинацию m способами,
где n комбинаций, то
n
n
Ậm =m .
34.
Задача о числе подмножеств данногомножества.
Пусть имеется М={ à1 , a 2 , a 3 ,..., a n }. Пустое множество Ø входит в это
множество как подмножество. Одноэлементные множества тоже. Поставим каждому
подмножеству кортеж длиной n, состоящий из 0 и 1.
0-если соответствующий элемент не входит в подмножество.
1-если входит.
Например,
подмножеству
{ a2 , a4 }
будет
соответствовать
кортеж
010100000….0000…
Для вех подмножеств получим (0,0,0,…0), (1,0,0,…0), (0,1,0,0,...,0)… (1,1,1,…1)
Кортежей столько, сколько подмножеств. Это размещения, состоящие из двух
элементов (0 и 1) и отличающиеся друг от друга либо элементами, либо их порядком.
Это размещения с повторениями из двух по n: Получим
n
n
Ậ2 =2 .
Таким образом, мы доказали теорему:
Число подмножеств n-элементного множества равно
2n .
0
1
Следствие: Так как число пустых подмножеств С n (0)=1, одноэлементных-С n =n,
2
3
n
двухэлементных-С n , трехэлементных-С n , n-элементных С n , то сумма
n
k 1
k
n
Сn =2 .
35.
Перестановки с повторениями.Пусть мы имеем n элементов
à1 , a 2 , a3 ,..., a n , Pn =n!. Пусть элемент à1
n
повторяется
k1 раз, элемент à 2 - k 2 раз,…., à n - k n раз, где
k
i 1
i
n . Тогда число
различных перестановок будет в
k1 ! меньше за счет одинаковых элементов à1 , в k 2
! раз меньше за счет одинаковых элементов à 2 ,…и в k n ! раз меньше за счет
одинаковых элементов à n . Тогда число различных перестановок будет равно:
n!
Pn ( k1 , k 2 ,…, k n )=
.
k1 !*k 2 !*... * k n !
Пример:
Сколько различных перестановок можно составить из слова МОЛОТОК?
Решение:
k1 (М)=1; k 2 (О)=3; k 3 (Л)=1; k 5 (Т)=1; k 7 (К)=1;
P7 (1,3,1,1,1)=
7!
=840.
1!*3!*1!*1!*1!
36.
Сочетания с повторениями.Пример:
На почте имеются открытки четырех видов: красные, желтые, зеленые и синие.
Требуется 10 открыток. Сколькими способами можно их скомбинировать?
Решение:
Пусть мы отобрали 4 красных, 2 желтых, 2 зеленых и 2 синих открытки. Составим
кортеж из 0 и 1. Выпишем столько единиц, сколько красная открытка встречается в
нашем наборе, и поставим 0: 11110. Затем добавим кортеж для желтых -110. Получим
11110110. Добавим кортеж для зеленых и синих открыток. В последнем 0 не ставим.
Получим кортеж 1111011011011. В нем 10 единиц и 3 нуля. Общая длина кортежа –
13. Таких кортежей можно составить столько, сколько перестановок с повторениями
из 13.
13!
P13 (10,3)=
=286 – это и будет число сочетаний с повторениями из 4 по 10.
10!*3!
10
C
P13 (10,3)= C 1013 Таким образом, Ĉ 10
13 .
4
В общем случае.
37.
Сочетания с повторениями.Пусть мы имеем n элементов
à1 , a 2 , a3 ,..., a n , из которых создаются сочетания с
повторениями, и каждое сочетание содержит k элементов. Составим кортеж, который
запишем вначале столько единиц, сколько элемент à1 входит в сочетание, затем
запишем 0. припишем кортеж из единиц и нуль для элемента
нуля. Получим: 111…1011…10…11…1
Единиц – k. Нулей – n-1. Длина кортежа n+ k-1
Общее число сочетаний с повторениями
(n k 1)!
k
Ĉ = Pn k 1 (k,n-(k-1))=
= C n k 1 ,
k!*(n (k 1))!
k
n
Итак,
k
Ĉ n =C
k
n k 1 ,
a 2 и т.д. без последнего
38.
БГТУ им. В.Г. ШуховаКафедра информационных технологий
Спасибо за внимание!




































 mathematics
mathematics








