Презентация _Метод графов в решении вероятностных задач (1)

1.

Метод графов в решении
вероятностных задач

2. План:

1. Повторить определение вероятности события,
свойства вероятности.
2. Повторить определение графа и дерева.
3. Рассмотреть решение задач методом графов.
4. Самостоятельно решить задачи на
использование метода графов.

3. Повторим: определение вероятности события

Вероятностью события А называют число, равное
отношению числа элементарных исходов, составляющих
событие А (m), к числу всех элементарных исходов
данного испытания (n):
m
Р( А)
n
классическое определение вероятности

4. Повторим: свойства вероятности события

1. Если событие А – невозможное (никогда не произойдет в
рамках данного испытания), то Р(А) = 0
и наоборот, если вероятность какого-либо события равна 0,
то это событие невозможное.
2. Если событие А – достоверное (обязательно
произойдет в рамках данного испытания), то Р(А) = 1
и наоборот, если вероятность какого-либо события равна 1,
то это событие достоверное.
3. Вероятность любого события – число из промежутка от 0
до 1.
0 ≤ Р(А) ≤ 1

5. Повторим: графы и деревья

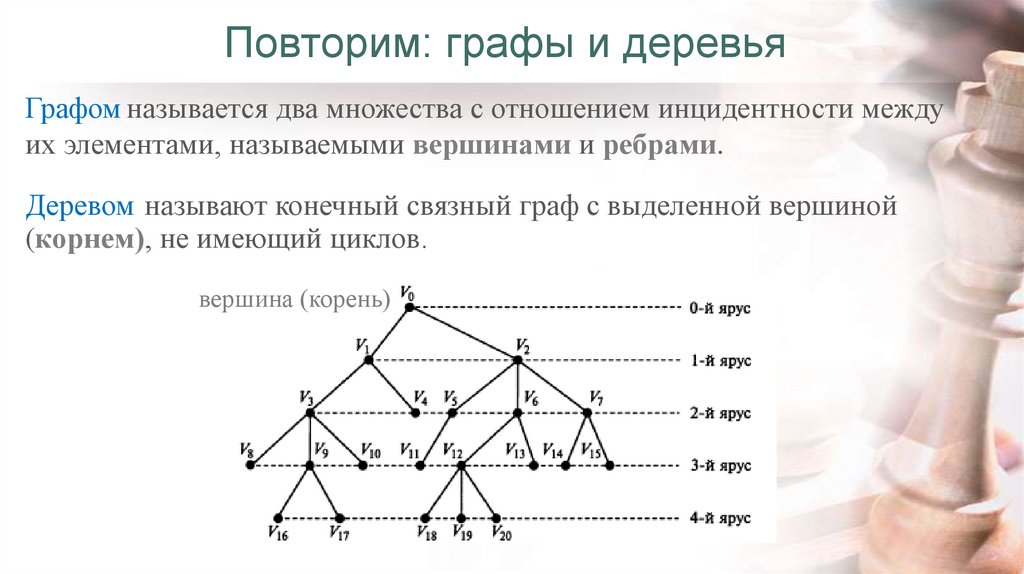
Графом называется два множества с отношением инцидентности между
их элементами, называемыми вершинами и ребрами.
Деревом называют конечный связный граф с выделенной вершиной
(корнем), не имеющий циклов.
вершина (корень)

6. Повторим: свойства деревьев

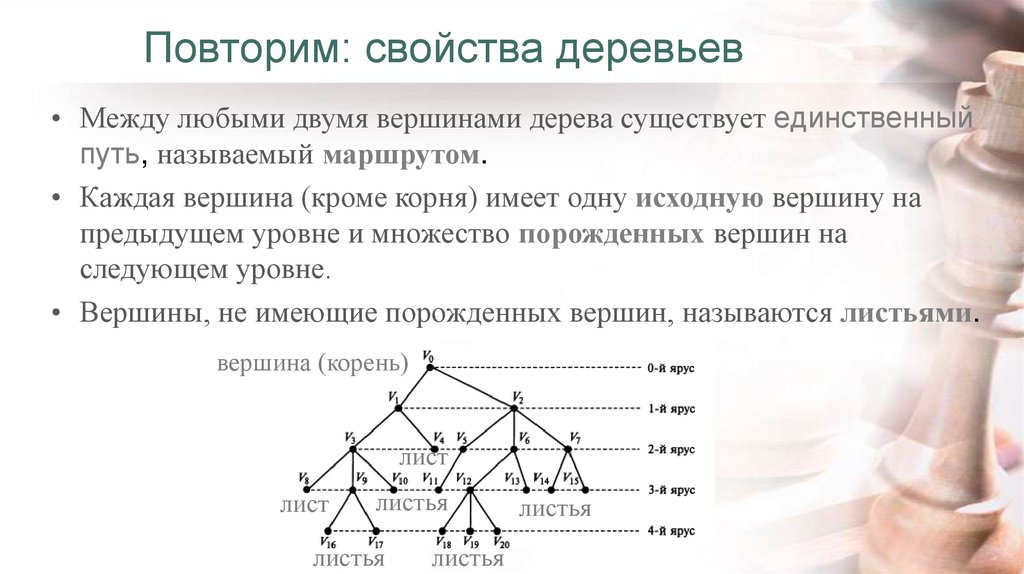
• Между любыми двумя вершинами дерева существует единственный
путь, называемый маршрутом.
• Каждая вершина (кроме корня) имеет одну исходную вершину на
предыдущем уровне и множество порожденных вершин на
следующем уровне.
• Вершины, не имеющие порожденных вершин, называются листьями.
вершина (корень)
лист
лист
листья
листья
листья
листья

7. Метод графов в решении вероятностных задач

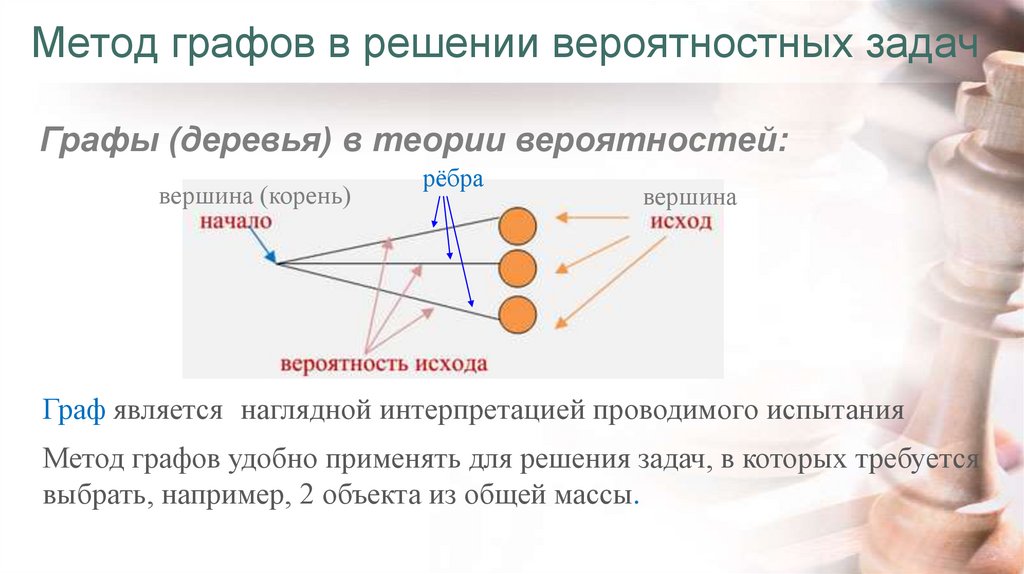
Графы (деревья) в теории вероятностей:
вершина (корень)
рёбра
вершина
Граф является наглядной интерпретацией проводимого испытания
Метод графов удобно применять для решения задач, в которых требуется
выбрать, например, 2 объекта из общей массы.

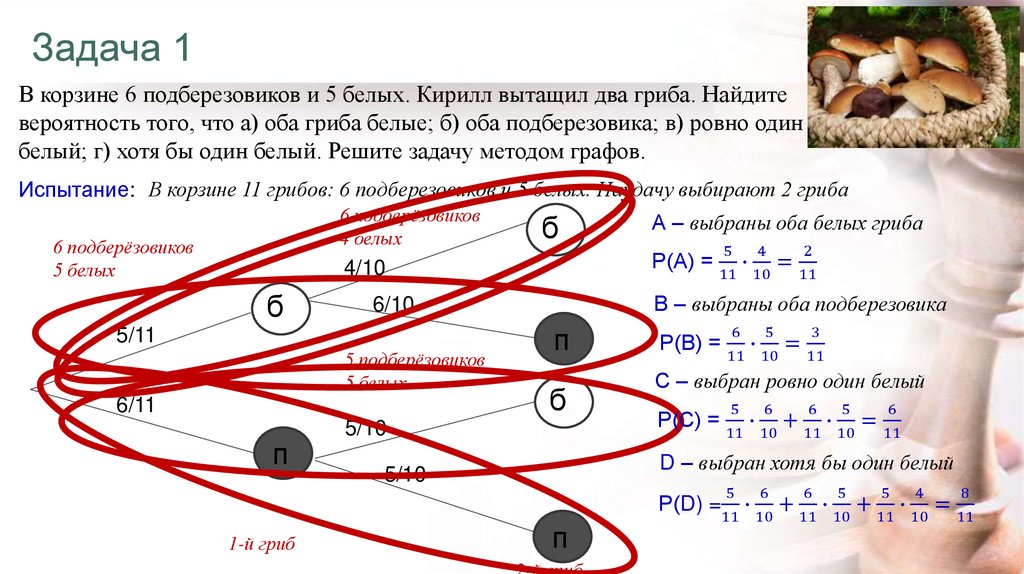
8. Задача 1

В корзине 6 подберезовиков и 5 белых. Кирилл вытащил два гриба. Найдите
вероятность того, что а) оба гриба белые; б) оба подберезовика; в) ровно один
белый; г) хотя бы один белый. Решите задачу методом графов.
Испытание: В корзине 11 грибов: 6 подберезовиков и 5 белых. Наудачу выбирают 2 гриба
6 подберёзовиков
4 белых
6 подберёзовиков
5 белых
б
Р(А) =
4/10
б
5 подберёзовиков
5 белых
6/11
п
5
4
2
∙ =
11 10
11
В – выбраны оба подберезовика
6/10
5/11
А – выбраны оба белых гриба
п
б
5/10
Р(В) =
С – выбран ровно один белый
Р(С) =
5
6
6
5
6
∙ + ∙ =
11 10
11 10
11
D – выбран хотя бы один белый
5/10
Р(D) =
1-й гриб
6
5
3
∙ =
11 10
11
п
5
6
6
5
5
4
8
∙ + ∙ + ∙ =
11 10
11 10
11 10
11

9.

Советы при решении задач:
сумма вероятностей на рёбрах графа, исходящих из одной вершины, равна 1;
вероятность искомого события можно получить, умножая вероятности,
встречающиеся на маршруте от корня до листа;
если нужно вычислить вероятность события, которому благоприятствует
несколько более простых событий, то вероятности этих событий складываем.

10. Задача 2

В фирме «ЯГК-трансфер» 10 машин Фольксваген и 5 Мерседес. ИС1-31
заказали две машины. Найдите вероятность того, что подадут а) два Мерседеса;
б) два Фольксвагена; в) ровно один Фольксваген; г) хотя бы один Мерседес.
Испытание: В фирме 15 машин: 10 Фольксваген и 5 Мерседес. Наудачу выбирают 2 машины
10 Фольксваген
4 Мерседес
10 Фольксваген
5 Мерседес
м
Р(А) =
4/14
м
9 Фольксваген
5 Мерседес
10/15
ф
5
4
2
∙ =
15 14
21
В – выбраны два Фольксвагена
10/14
5/15
А – выбраны два Мерседеса
ф
м
5/14
Р(В) =
С – выбран ровно один Фольксваген
10 5
5 10
Р(С) = ∙ + ∙
15 14
15 14
=
10
21
D – выбран хотя бы один Мерседес
9/14
Р(D) =
1-й автомобиль
10 9
3
∙ =
15 14
7
ф
10 5
5 10
5
4
13
∙ + ∙ + ∙ =
15 14
15 14
15 14
21

11. Задачи для самостоятельного решения:

1. В корзине лежат 3 белых и 4 черных шара. Из корзины достают случайным
образом 2 шара. Чему равна вероятность того, что: 1) все шары окажутся белыми, 2)
выбраны только черные шары, 3) выбраны один белый и один черный шар, 4) шары
одного цвета, 5) достали хотя бы один белый шар?
2. В партии из 8 деталей имеется 6 стандартных. Найти вероятность того, что среди
взятых наугад двух деталей 1) одна стандартная, а одна нет, 2) обе стандартные, 3)
обе нестандартные, 4) хотя бы одна стандартная.
3. Трое друзей выбирают дежурного при помощи спички: обламываю одну из трёх
спичек, каждый по очереди тянет спичку. Дежурит тот, кто вытащит короткую
спичку. Найдите вероятности дежурить тому, кто стоит 1) первым; 2) вторым; 3)
третьим.
4. *Историческая задача де Мере. Франция, первая половина XVII века. Опытный и
азартный игрок шевалье де Мере обращается к Блезу Паскалю с просьбой помочь в
разрешении двух вопросов. Вот один из них: Двое играют в «орлянку» до пяти
побед. Игра прекращена, когда первый выиграл четыре партии, а второй – три. Как
в этом случае следует поделить первоначальную ставку?