Основные соотношения_Треугольник

1. ОСНОВНЫЕ СООТНОШЕНИЯ МЕЖДУ ЭЛЕМЕНТАМИ ТРЕУГОЛЬНИКОВ

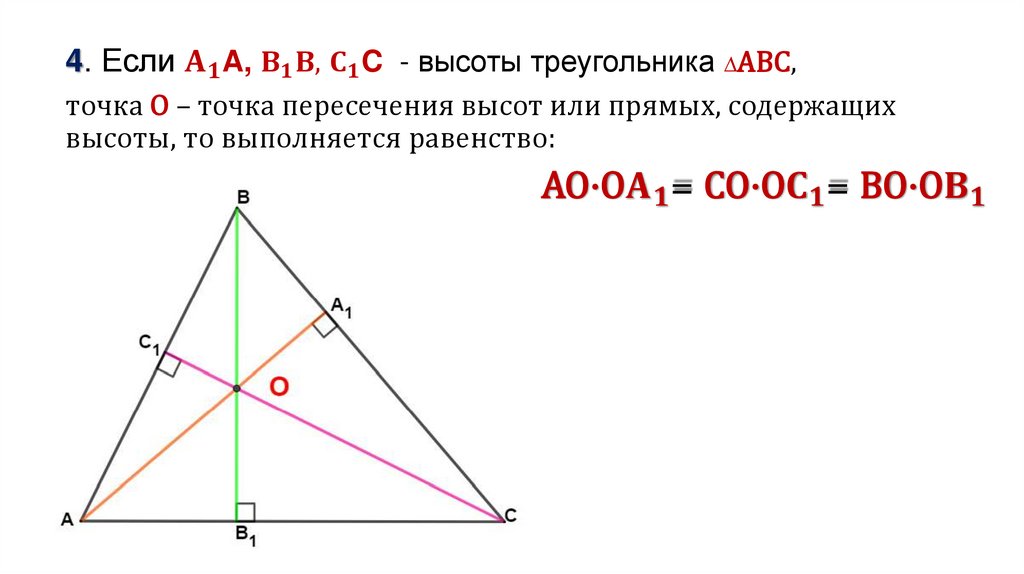
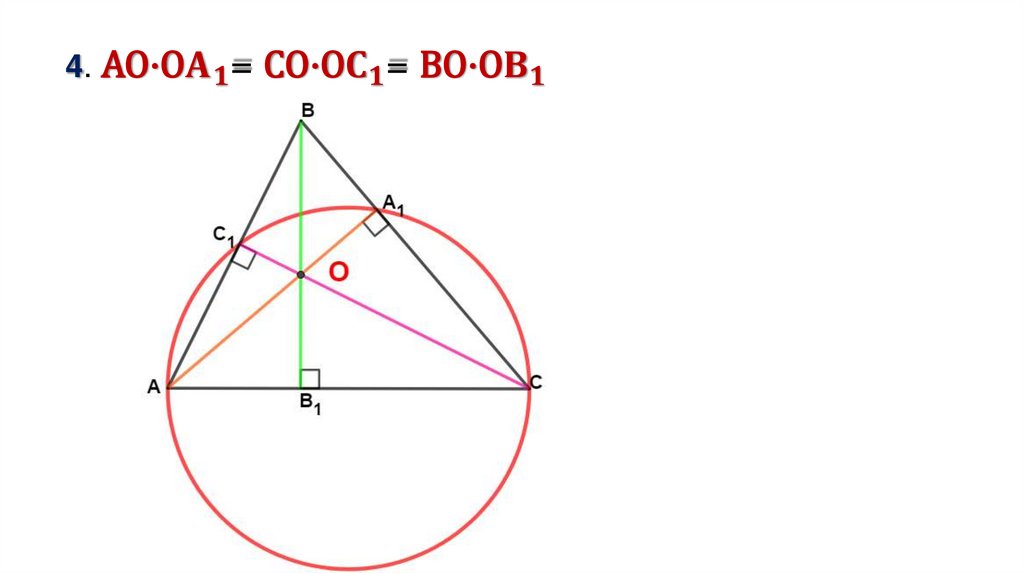
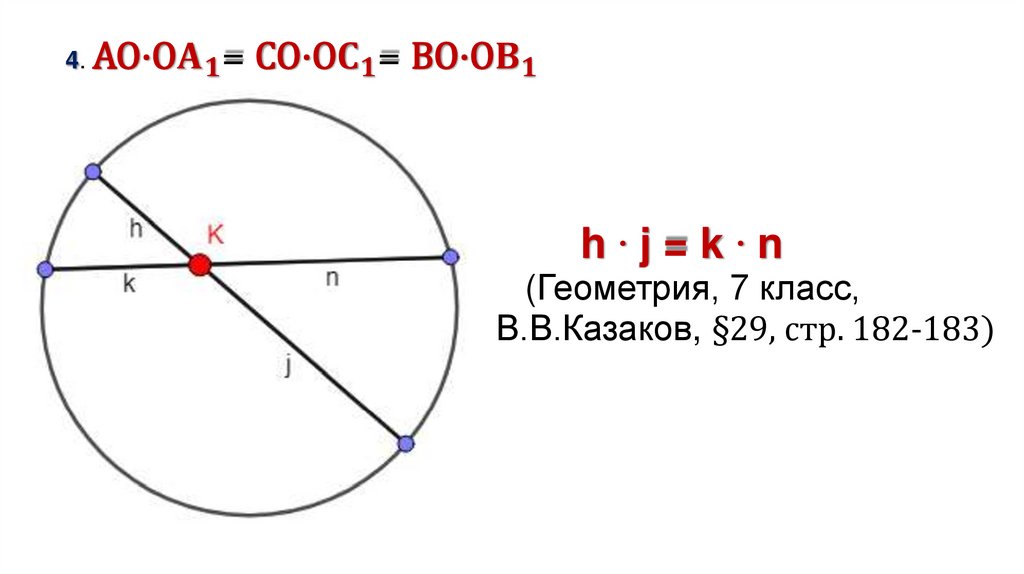
§ 1 Дополнительные свойства высот
Точка пересечения высот или прямых, содержащих высоты
любого треугольника называется ортоцентром.

2. ОСНОВНЫЕ СООТНОШЕНИЯ МЕЖДУ ЭЛЕМЕНТАМИ ТРЕУГОЛЬНИКОВ

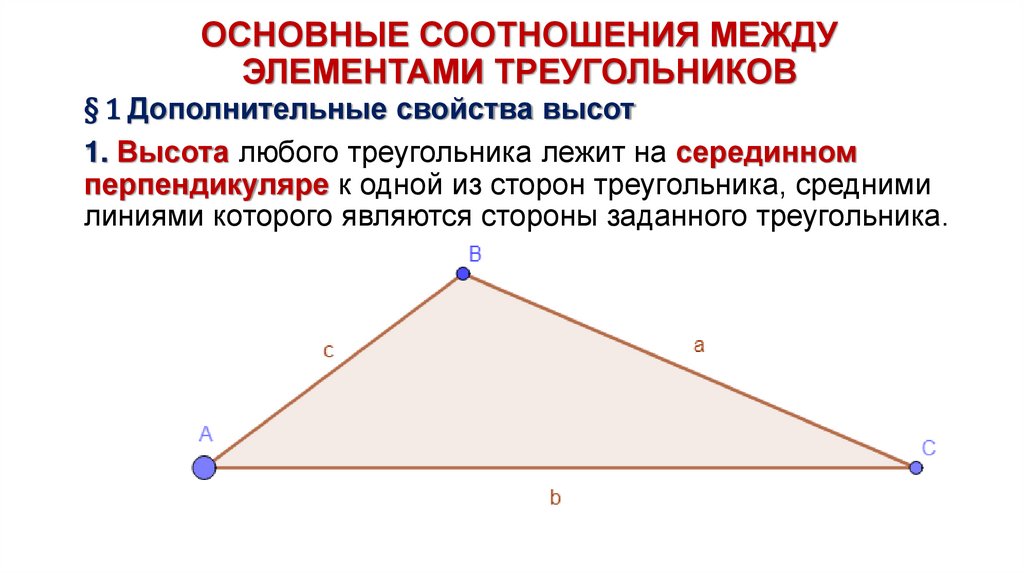
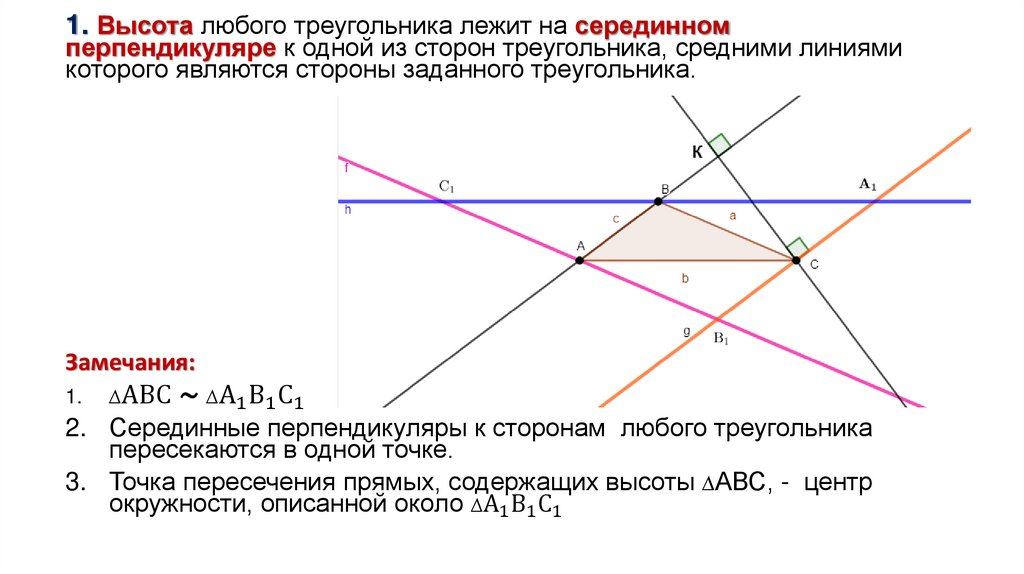
§ 1 Дополнительные свойства высот
1. Высота любого треугольника лежит на серединном
перпендикуляре к одной из сторон треугольника, средними
линиями которого являются стороны заданного треугольника.

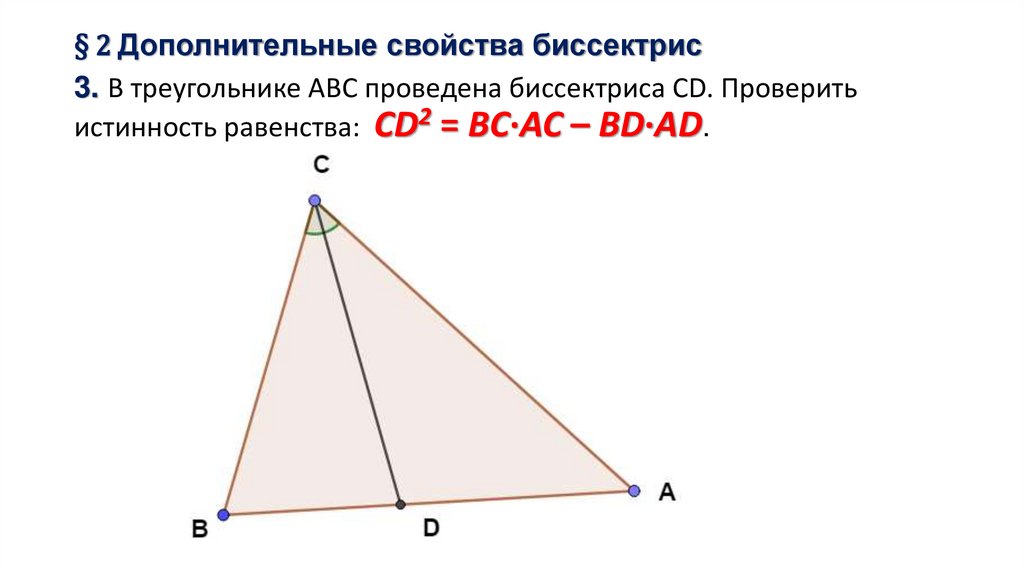
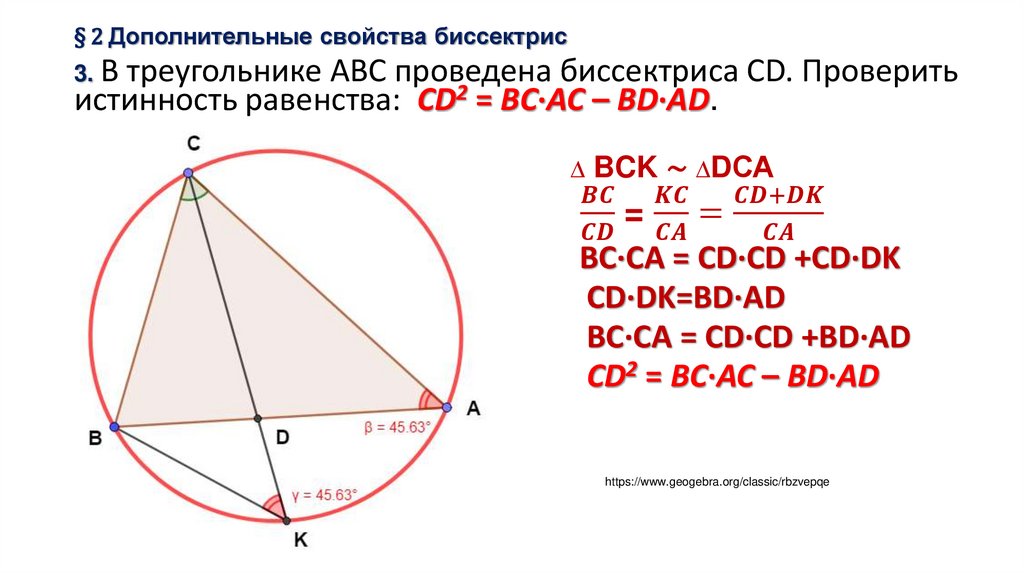
3.

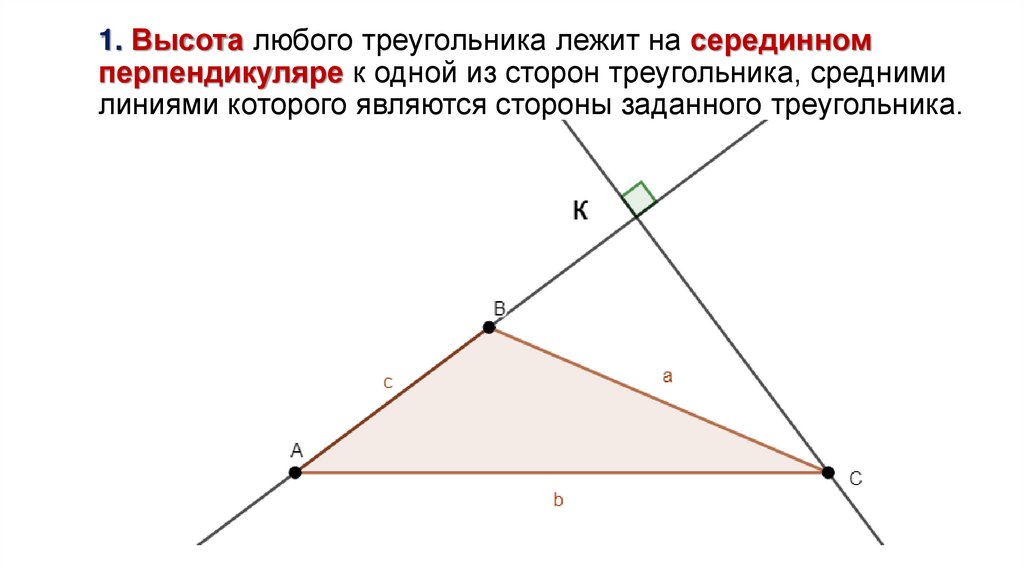
1. Высота любого треугольника лежит на серединном
перпендикуляре к одной из сторон треугольника, средними
линиями которого являются стороны заданного треугольника.

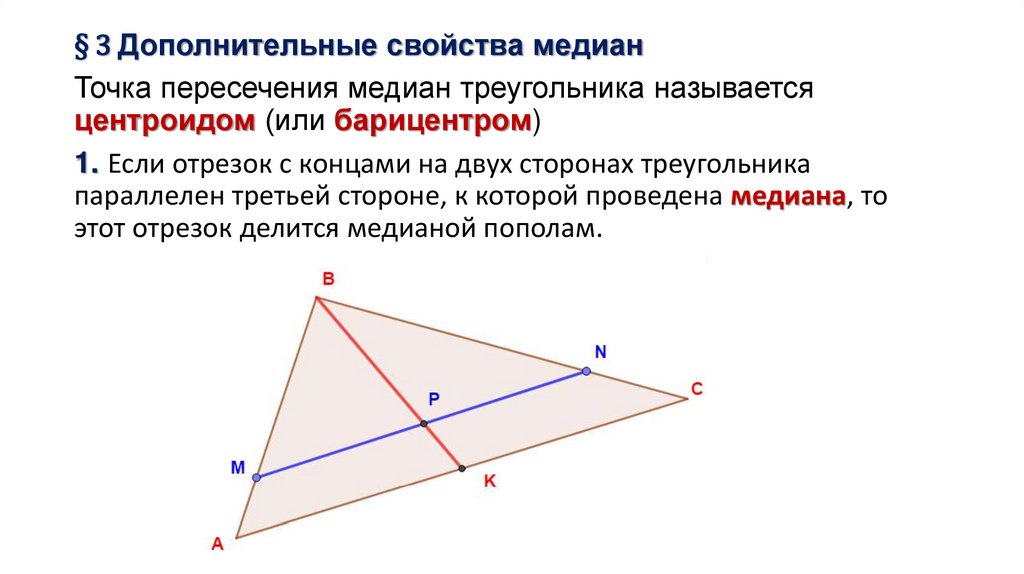
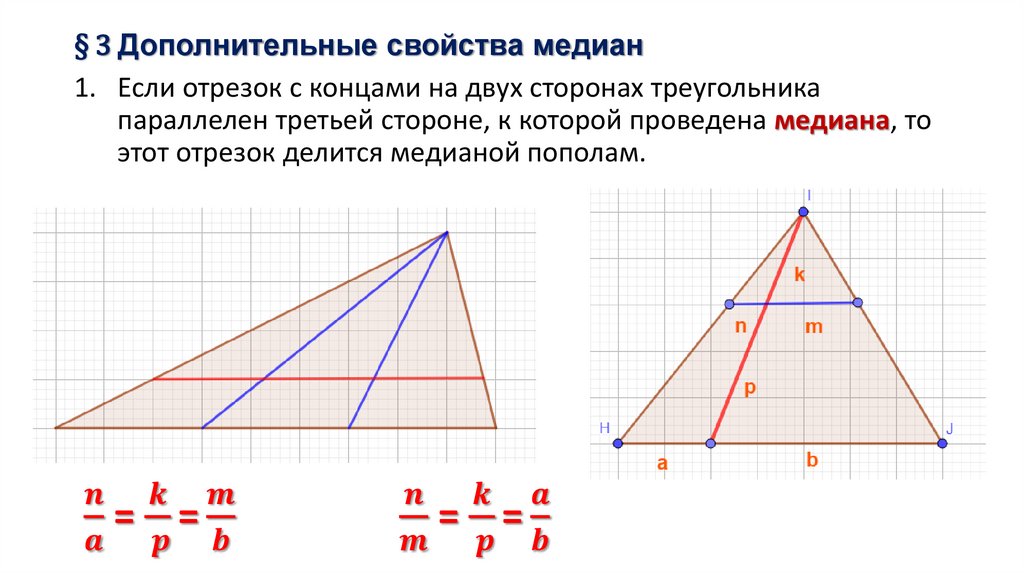
4.

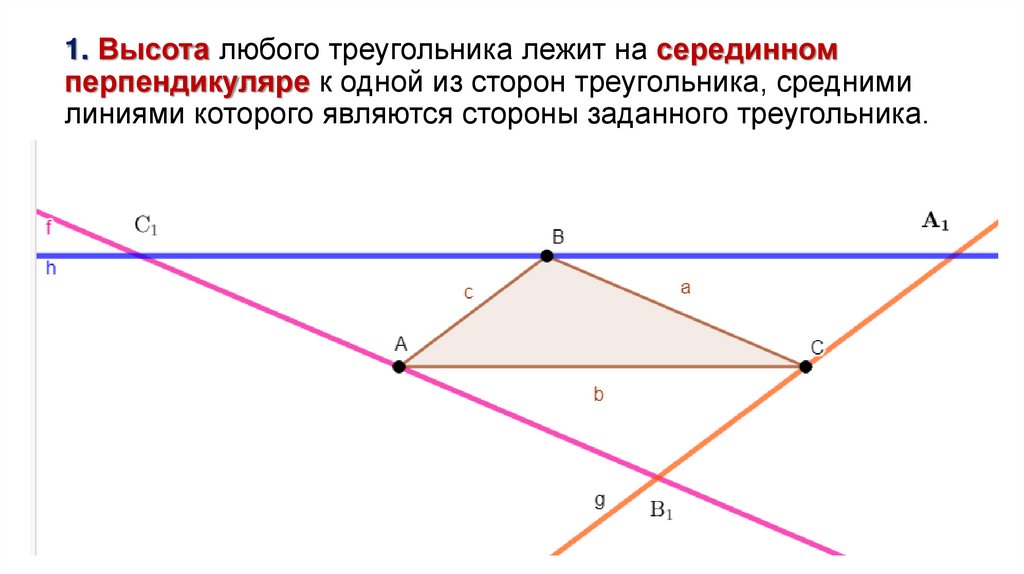
1. Высота любого треугольника лежит на серединном
перпендикуляре к одной из сторон треугольника, средними
линиями которого являются стороны заданного треугольника.

5.

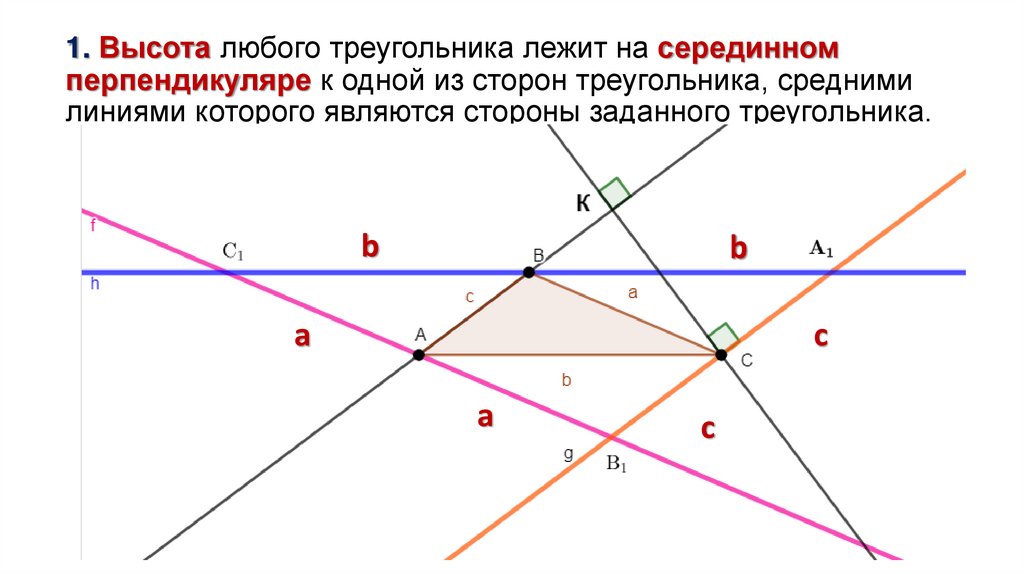
1. Высота любого треугольника лежит на серединном
перпендикуляре к одной из сторон треугольника, средними
линиями которого являются стороны заданного треугольника.
b
a
c
a
c

6.

1. Высота любого треугольника лежит на серединном
перпендикуляре к одной из сторон треугольника, средними линиями
которого являются стороны заданного треугольника.
Замечания:
1.
∆АВС ∼ ∆А1 В1 С1
2. Серединные перпендикуляры к сторонам любого треугольника
пересекаются в одной точке.
3. Точка пересечения прямых, содержащих высоты ∆АВС, - центр
окружности, описанной около ∆А1 В1 С1

7.

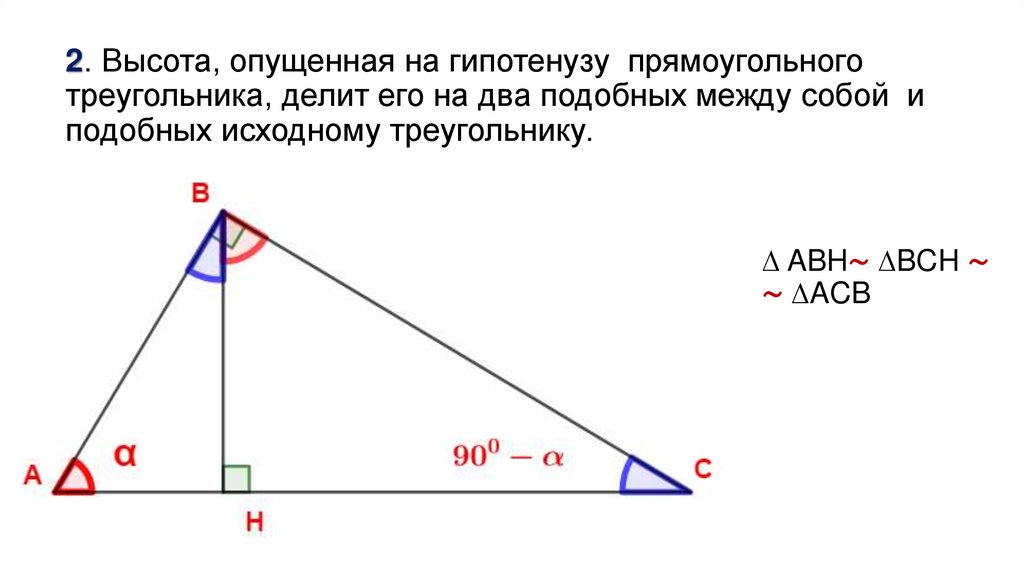
2. Высота, опущенная на гипотенузу прямоугольного
треугольника, делит его на два подобных между собой и
подобных исходному треугольнику.
∆ ABH∼ ∆BCH ∼
∼ ∆ACB

8.

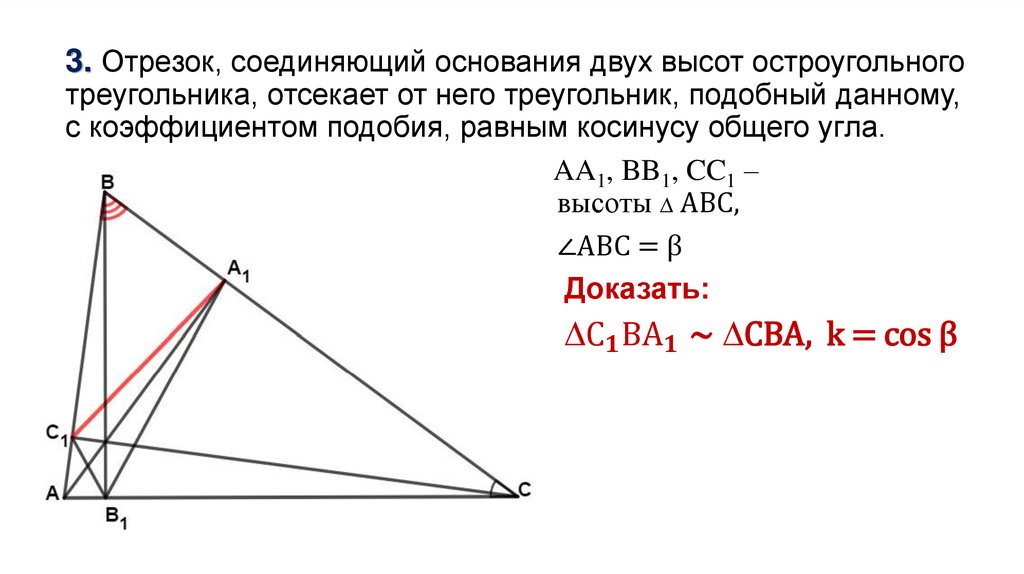
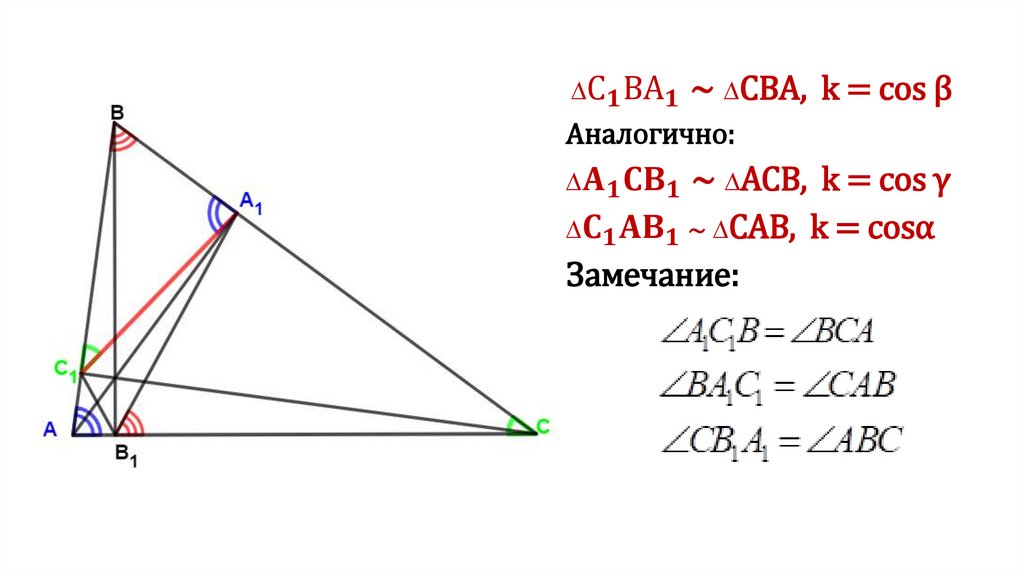
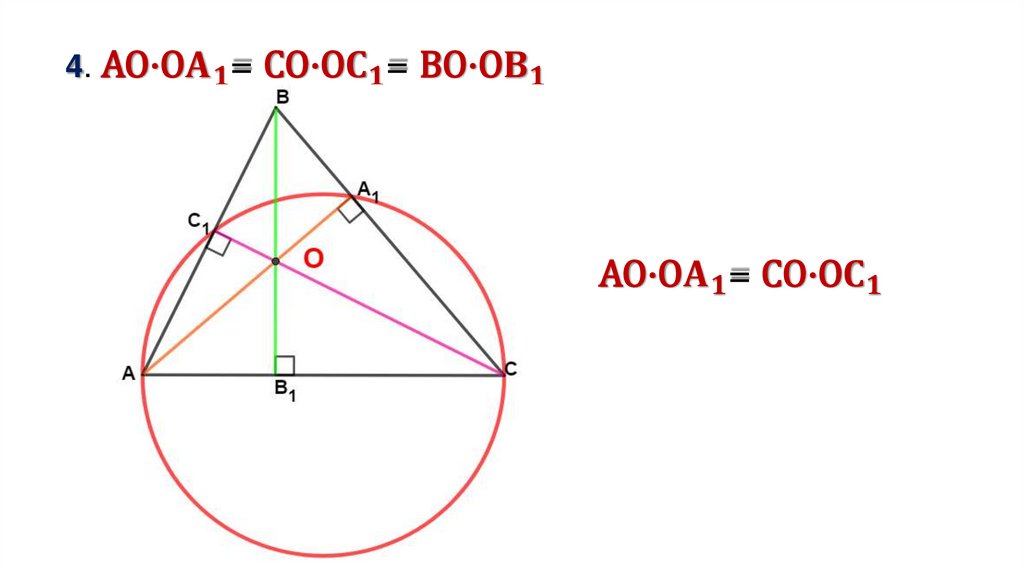
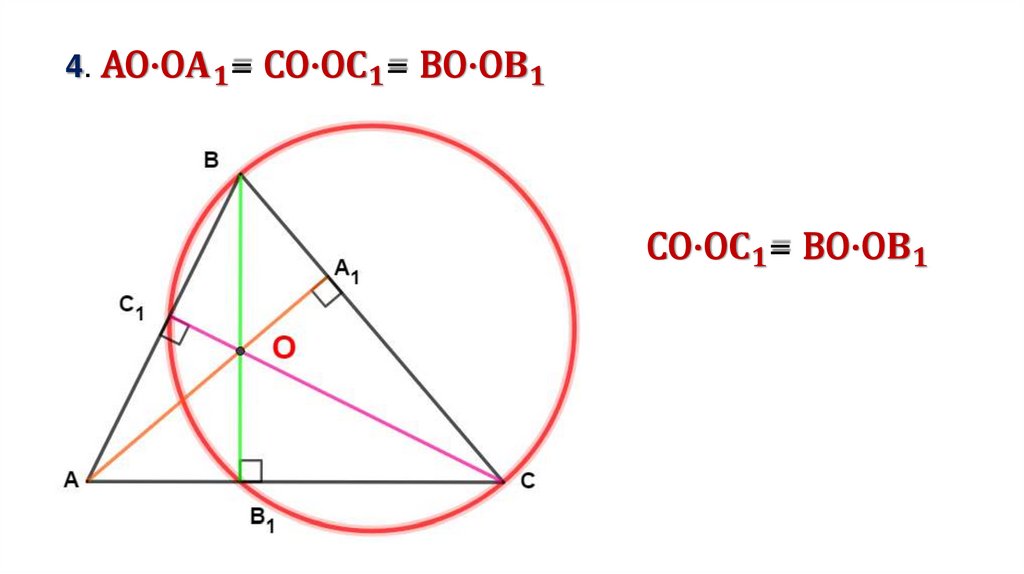
3. Отрезок, соединяющий основания двух высот остроугольного
треугольника, отсекает от него треугольник, подобный данному,
с коэффициентом подобия, равным косинусу общего угла.
AA1, BB1, CC1 –
высоты ∆ АВС,
∠АВС = β
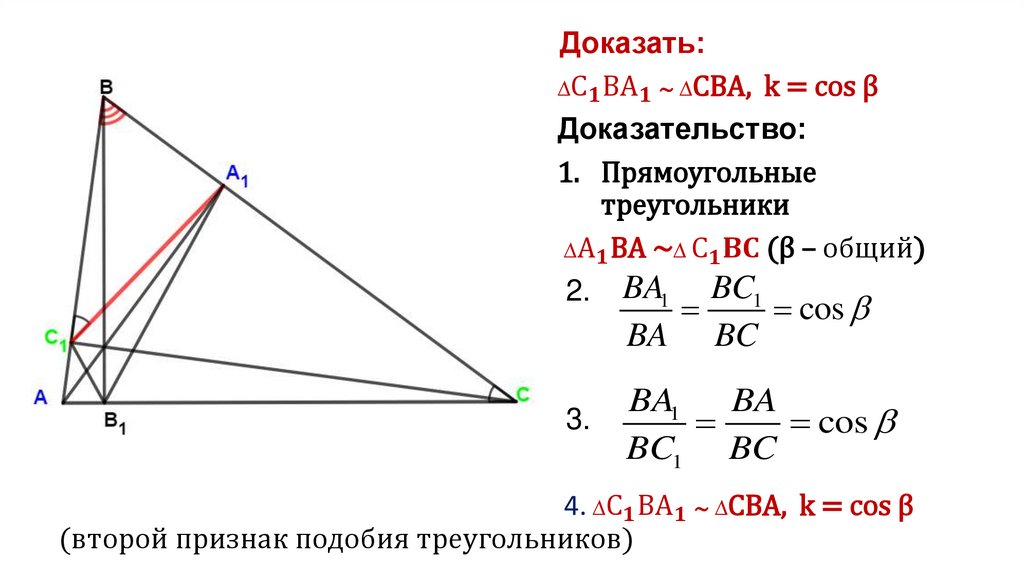
Доказать:
∆С