Лекция Логистическая регрессия (1)

1. Машинное обучение и нейросетевые технологии

2.

Кол-во
Кол-во
аудиторных часов лекционных часов
92
50
Кол-во часов
практических
занятий
42
Формы
промежуточной
аттестации
Контрольная,
экзамен

3. Логистическая регрессия

Логистическая регрессия (логит модель) — классический метод
классификации в машинном обучении. Модель логистической
регрессии является линейной моделью.
Пусть X — непрерывная случайная величина. X подчиняется
логистическому распределению, означает, что X имеет следующую
функцию распределения
и функцию плотности:
где μ параметр положения, и γ > 0 параметр формы.

4. Логистическая регрессия

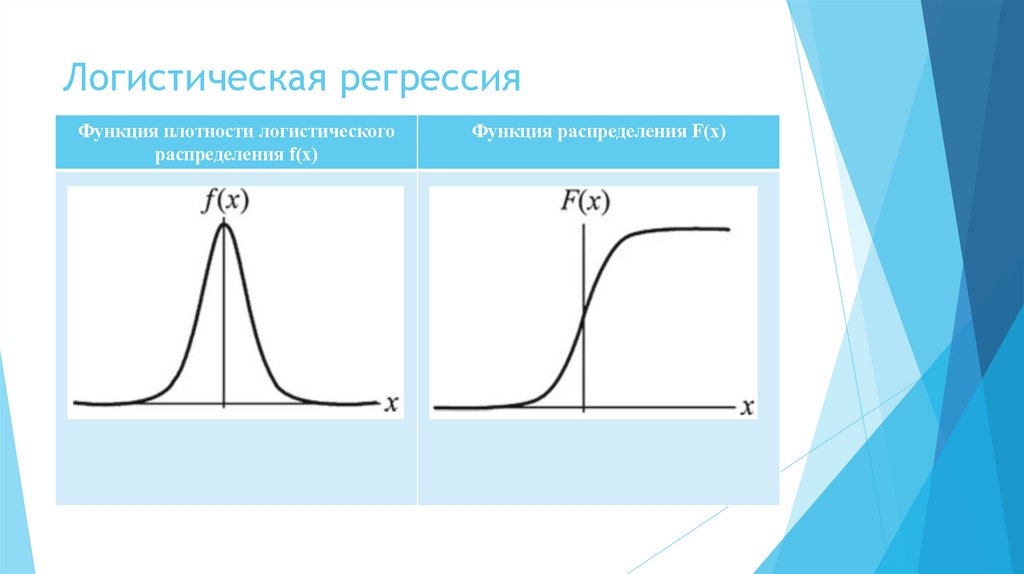
Функция плотности логистического
распределения f(x)
Функция распределения F(x)

5. Логистическая регрессия

Функция распределения F(x) является логистической функцией, а ее
график представляет собой S-образную кривую (сигмоидальную
кривую). Кривая симметрична относительно центра в точке (μ, ½) и
удовлетворяет условию
F(-x + μ) – ½= -F(x + μ) + ½ .
Кривая растет быстрее вблизи центра и медленнее на концах. Чем
меньше значение параметра формы γ, тем быстрее кривая растет
вблизи центра.

6. Логистическая регрессия

Модель биномиальной логистической регрессии — это классификационная модель,
представленная условным распределением вероятностей P(Y|X) в форме
параметрического логистического распределения. Здесь случайная величина X — это
действительное число, а случайная величина Y принимает значение 1 или 0. Мы
оцениваем параметры модели с помощью контролируемого обучения.
Модель биномиальной логистической регрессии — это условное вероятностное
распределение удовлетворяющее выражениям
где x ∈ Rn — вход, Y ∈ {0, 1} — выход, w ∈ Rn и b ∈ Rn — параметры, w называется
вектором веса, b называется смещением, а w · x — внутреннее произведение w и x.

7. Логистическая регрессия

То есть для заданного входного экземпляра x можно получить P(Y = 1|x ) и P(Y =
0|x ) в соответствии с равенствами из определения.
Логистическая регрессия сравнивает величину двух значений условной
вероятности и присваивает экземпляр x классу с большим значением вероятности.
Иногда вектор веса и входной вектор расширяются для удобства. Они попрежнему обозначаются как w и x, т. е.
w=(w(1), w(2), · · · , w(n), b)T, x=(x(1),x(2),…,x(n),1)T.
На этом этапе модель логистической регрессии выглядит следующим образом:

8. Логистическая регрессия

Теперь рассмотрим характеристики модели логистической регрессии. Шансы
события — это отношение вероятности того, что событие произойдет, к вероятности
того, что событие не произойдет. Если вероятность события равна p, то шансы
события выражаются как p/(1−p). Логарифм шансов (логит-функция) этого события
равен: log it(p)=log(p/(1-p)) или
Это означает, что в модели логистической регрессии логарифм шансов выхода Y=1
является линейной функцией входа x. Другими словами, логарифм шансов выхода Y=1
является моделью, представленной линейной функцией входа x, т. е. моделью
логистической регрессии.

9. Логистическая регрессия

С другой точки зрения рассмотрим линейную функцию w · x, которая
классифицирует вход x, область значений которой — все действительные числа.
Обратите внимание, что здесь x ∈ Rn+1, w ∈ Rn+1.
По определению формулы модели логистической регрессии линейная функция w·x
может быть преобразована в вероятность
При этом, чем ближе значение линейной функции к положительной
бесконечности, тем ближе значение вероятности к 1; чем ближе значение линейной
функции к отрицательной бесконечности, тем ближе значение вероятности к 0.
Такая модель является моделью логистической регрессии.

10. Оценка параметров модели

Если модель логистической регрессии обучается, на заданном наборе данных
T={(x1, y1), (x2, y2), …, (xN, yN)}, где xi ∈ Rn, yi∈{0, 1}, параметры модели можно
оценить, применив метод оценки максимального правдоподобия для получения
модели логистической регрессии. Предположим, что: P(Y = 1|x) = π(x), P(Y = 0|x) =
1 − π(x).
Функция правдоподобия равна
логарифмическая функция правдоподобия равна

11. Оценка параметров модели

Найдите максимальное значение логарифмической функции
правдоподобия L(w), чтобы получить оценочное значение w. Таким образом,
задача становится задачей оптимизации с логарифмической функцией
правдоподобия в качестве целевой функции. Методы, обычно используемые
в обучении логистической регрессии: метод градиентного спуска и метод
квазиньютона. Предположим, что оценка максимального правдоподобия w
равно