Similar presentations:
Основы теории вероятностей. Тема 2
1.
Тема 2. Основы теориивероятностей
П.1 Случайные события. Операции над событиями
2.
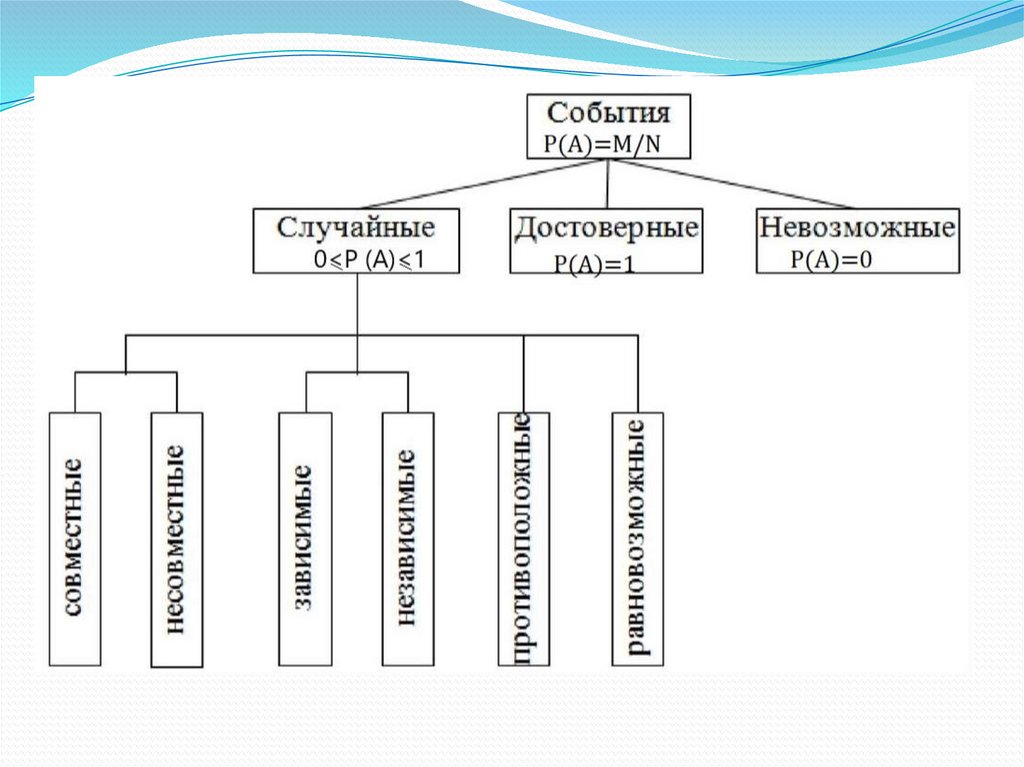
Основные понятияСобытие
Случайное событие
Достоверное событие
Невозможное событие
Совместные, несовместные события
Зависимые, независимые события
Противоположные события
Благоприятствующее событие
Равновозможные события
Полная группа событий
Операции над событиями
Классическая формула вероятности
Свойства вероятности
3.
Под событием понимается явление, котороепроисходит в результате осуществления какоголибо определенного комплекса условий.
Осуществление этого комплекса условий
называется опытом или испытанием.
Случайным называется событие, которое может
произойти или не произойти в результате
некоторого испытания (опыта).
4.
Событие называется достоверным,если оно обязательно произойдет в
результате данного испытания.
Событие называется невозможным,
если оно не может произойти в
результате данного испытания.
5.
Пример 1В корзине 10 шаров синего цвета.
Вынимаем 1 шар.
Событие А - «достали шар синего цвета»достоверное
Событие В - «достали шар красного
цвета»- невозможное
6.
События А и В называютсянесовместными, если в результате данного
испытания появление одного из них
исключает появление другого.
События А и В называются совместными,
если в результате данного испытания
появление одного из них не исключает
появления другого.
7.
Пример 2Бросаем пятирублевую монету 1 раз.
А-«появилась решка»,
В-«появился герб»,
С-«появилась цифра 5».
А и В – несовместные,
А и С – совместные.
8.
Если одно событие влияет на результатдругого события , то оно называется
зависимым событием.
Если одно событие не влияет на результат
другого события, то оно называется
независимым.
9.
Пример 3При подбрасывании двух или большего
количества монет вероятность выпадения орла
или решки на любой монете не зависит от
того, что выпадет на других монетах .
Событие А – «на экзамене студенту достанется
простой билет».
Если студент идет не самым первым, то
событие А будет зависимым, поскольку его
вероятность зависит от того, какие билеты уже
вытянули однокурсники.
10.
Два события А иА называются
противоположными или взаимно
дополнительными, если непоявление
одного из них в результате данного
испытания влечет появление другого.
11.
Пример 4«Изделие бракованное» и «изделие
стандартное» - противоположные
события
«натуральное число четное» и
«натуральное число нечетное» противоположные события
12.
Событие А называетсяблагоприятствующим событию В, если
появление события А влечет за собой
появление события В.
События называются
равновозможными, если по условию
испытания нет основания считать какоелибо из них более возможным, чем любое
другое.
13.
Пример 5Бросается игральный кубик. На верхней
грани кубика появится любое из шести
событий: выпало 1,2,3,4,5,6 очков.
Выпадение любого из шести событий –
равновозможные.
Выпадение четного числа очков
благоприятствующие выпадение 2,4 или 6
14.
Если группа событий такова, что в результатеиспытания обязательно должно произойти хотя бы
одно из них и любые два из них несовместны, то
эта группа событий называется полной группой
событий.
Каждое событие из полной группы попарно
несовместных событий называется исходом или
элементарным событием.
15.
Пример 6Производится один выстрел по мишени. Выделим
следующие события:
Аi – «выбито i очков, где i изменяется от 0 до 10»,
В – «выбито четное число очков»,
С - «выбито нечетное число очков»,
D - «выбито более 4 очков»,
E - «выбито менее 5 очков»,
F - «число выбитых очков делится на 11»,
K – «число выбитых очков меньше 12»
16.
Укажите:1.
2.
3.
4.
5.
6.
7.
8.
9.
Случайное событие
Достоверное событие
Невозможное событие
Несовместные события
Совместные события
Противоположные события
Благоприятствующее событие
Равновозможные события
Полная группа событий
17.
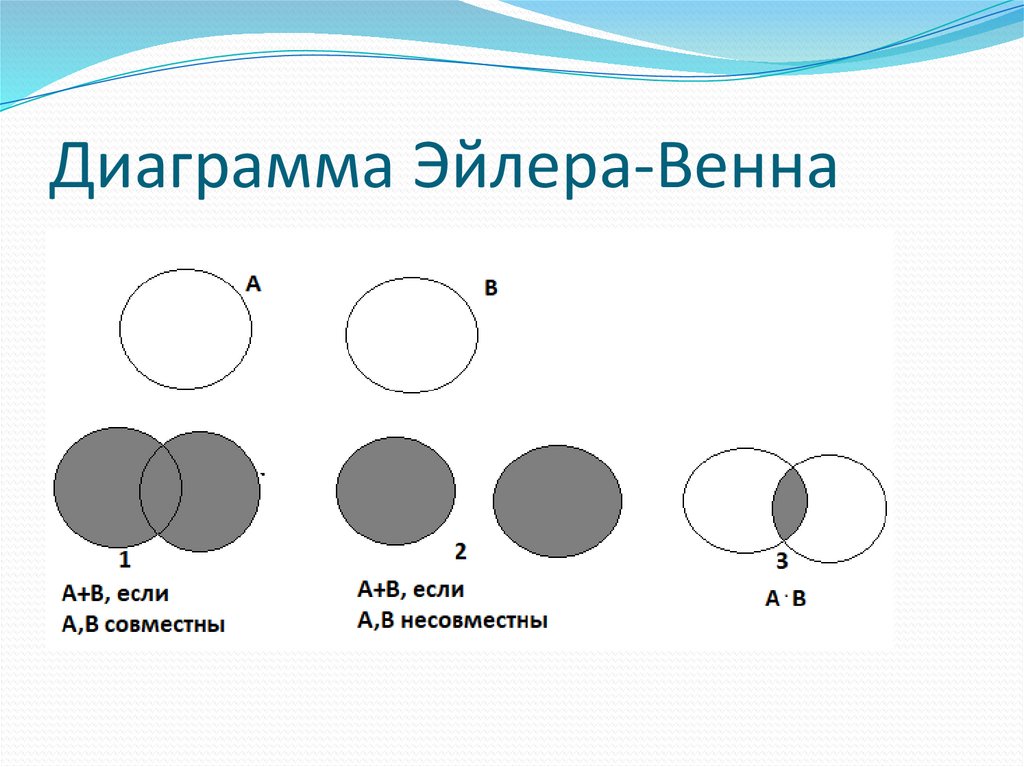
Операции над событиямиСуммой нескольких событий
называется событие, состоящее в
наступлении хотя бы одного из них в
результате испытания.
Если А и В совместные события, то сумма А+В
означает, что наступит событие А, или событие В,
или оба события вместе.
Если же события несовместны, то сумма А+В
заключается в наступлении события А или
события В.
18.
Пример 7Данные их примера 5
А6+С ={ 6 }+{1,3,5,7,9}={1,3,5,6,7,9}
В+D = { 2,4,6,8,10 }+{5,6,7,8,9,10}=
{2,4,5,6,7,8,9,10}
Е+К=
D+Е=
19.
Произведением нескольких событийназывается событие, состоящее в
совместном наступлении всех этих
событий в результате испытания.
А В означает , что наступило событие А и
событие В
20.
Пример 8А- «из колоды карт вынута ДАМА»
В- «из колоды карт вынута карта пиковой масти»
А+В
АВ
21.
Пример 9Данные их примера 6
А6*С ={ 6 }*{1,3,5,7,9}= О
В*D = { 2,4,6,8,10 }*{5,6,7,8,9,10}= {6, 8,10}
Е*К=
D*Е=
22.
Диаграмма Эйлера-Венна23.
П2. Классическоеопределение вероятности
Вероятность события – это численная
мера объективной возможности его
появления.
24.
Пусть имеется полная группа попарно несовместныхсобытий и равновозможных событий.
Вероятность Р(А) наступления события А
вычисляется как отношение числа исходов,
благоприятствующих наступлению события, к
числу всех исходов испытания.
Если N – число всех исходов испытания, а
М – число исходов, благоприятствующих событию А,
то
M
P( A)
N
25.
Пример 10В группе 30 учащихся. Из них 12 юношей,
остальные – девушки. Известно, что к
доске должны быть вызваны двое
учащихся. Какова вероятность, что это
девушки?
26.
Решение:M C182
51
P(A)
2
0.35
N C30 145
27.
Пример 11Бросают два игральных кубика.
Какова вероятность того, что сумма
выпавших очков меньше 13?
28.
M 36P( A)
1
N 36
29.
Пример 12Цифры 0,1,2,3,4,5,6,7,8,9 написаны на
карточках, которые тщательно
перемешаны. Произвольным образом
вынимаются подряд три карточки и
кладутся в ряд. Какова вероятность того,
что число, составленное из трех цифр,
которые написаны на карточках, больше
987?
30.
M 0P( A)
0
N N
31.
Свойства вероятности1. Вероятность достоверного события равна 1
2. Вероятность невозможного события равна 0
3. Вероятность события А удовлетворяет
двойному неравенству
0 Р ( А) 1






























 mathematics
mathematics








