Симметрия в пространстве

1. Симметрия в пространстве

2. Понятие преобразования для фигур в пространстве определяется так же, как и на плоскости. Так же, как и на плоскости, определяются преобразо

Понятие преобразования для фигур в
пространстве определяется так же,
как и на плоскости. Так же, как и на
плоскости, определяются
преобразования симметрии
относительно точки и прямой. Кроме
симметрии относительно точки и
прямой в пространстве,
рассматривают преобразование
симметрии относительно плоскости.

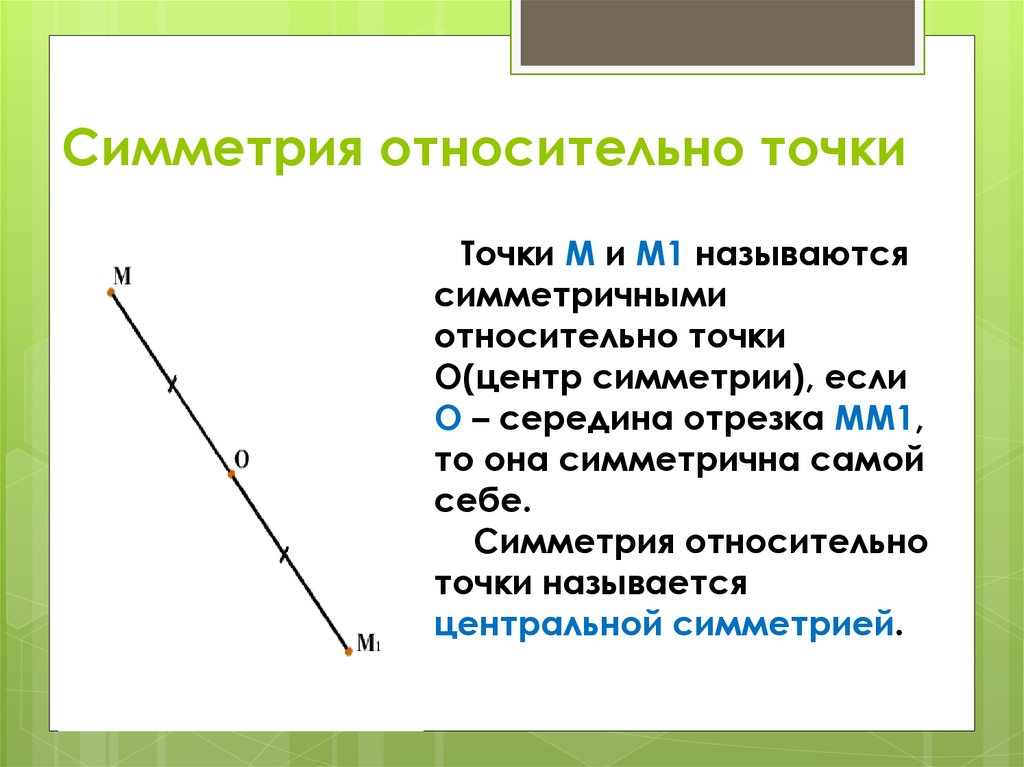
3. Симметрия относительно точки

Точки М и М1 называются
симметричными
относительно точки
О(центр симметрии), если
О – середина отрезка ММ1,
то она симметрична самой
себе.
Симметрия относительно
точки называется
центральной симметрией.

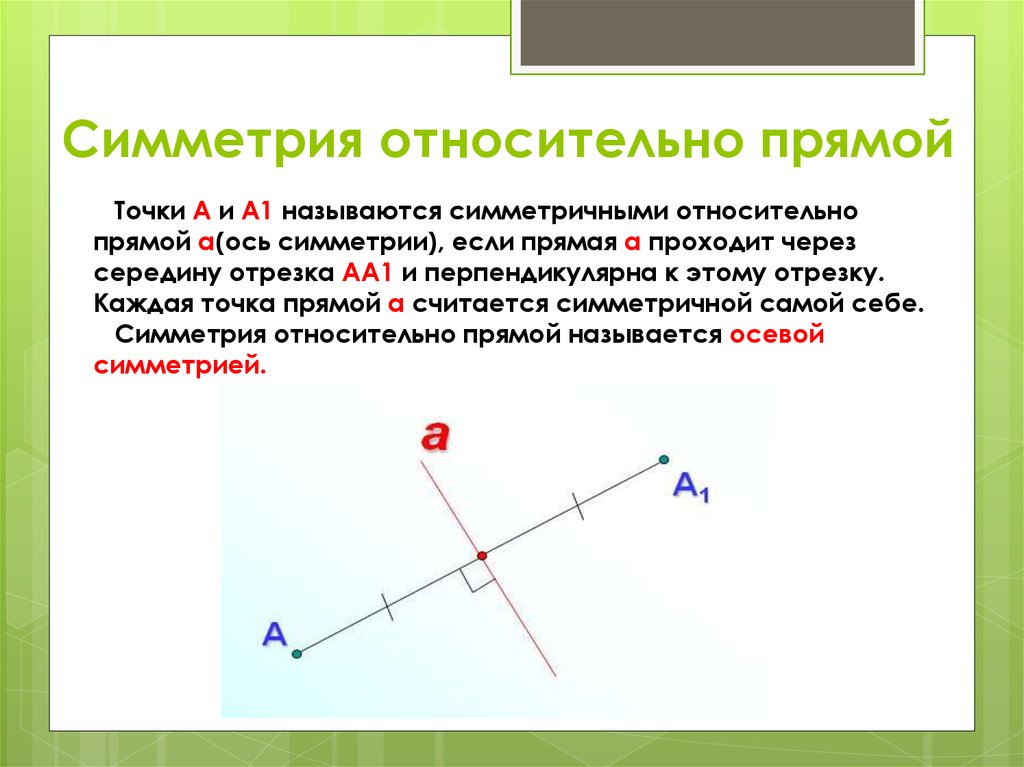
4. Симметрия относительно прямой

Точки А и А1 называются симметричными относительно
прямой а(ось симметрии), если прямая а проходит через
середину отрезка АА1 и перпендикулярна к этому отрезку.
Каждая точка прямой а считается симметричной самой себе.
Симметрия относительно прямой называется осевой
симметрией.

5. Симметрия относительно плоскости

Это преобразование состоит в следующем. Пусть —
произвольная фиксированная плоскость. Из точки X фигуры
опускаем перпендикуляр ХА на плоскость α и на его продолжении
за точку А откладываем отрезок АХ', равный ХА. Точка X' называется
симметричной точке X относительно плоскости α, а
преобразование, которое переводит точку X в симметричную ей
точку X', называется преобразованием симметрии относительно
плоскости α.
Если точка X лежит в плоскости α, то
считается, что точка X переходит в
себя. Если преобразование
симметрии относительно плоскости
α переводит фигуру в себя, то
фигура называется симметричной
относительно плоскости α, а
плоскость α называется плоскостью
симметрии этой фигуры.

6. Зеркальная симметрия (преобладает в животном и растительном мире)

7. Вращательная(поворотная) симметрия

8. Скользящая симметрия