Основы программирования. Рекурсивные алгоритмы

1. Основы программирования

Рекурсивные алгоритмы
1

2. Рекурсивные объекты и алгоритмы

Рекурсивный объект – это объект, который является
частью самого себя. Классический пример бесконечной
рекурсии – это изображение, которое формируется в двух
направленных друг на друга зеркалах.
В информатике рекурсивным называют алгоритм, который
в процессе выполнения вызывает сам себя.
Рекурсия позволяет описать потенциально бесконечные
вычисления без копирования частей программы и без
циклов. Во многих случаях рекурсия позволяет построить
простой и изящный алгоритм.
Рекурсия может быть прямой (функция вызывает саму
себя) и косвенной (например, имеются функции F1 и F2,
при этом F1 вызывает F2, а F2 вызывает F1).
2

3. Рекурсивные алгоритмы

Для любого рекурсивного алгоритма должны выполняться
следующие требования:
• рекурсивный алгоритм должен быть оформлен в виде
функции (чтобы его можно было вызвать)
• рекурсивный
алгоритм должен включать один или
несколько базисных вариантов, при достижении которых
последующие рекурсивные вызовы не производятся
• рекурсивная функция должна содержать по крайней
мере один параметр, значения которого изменяются при
каждом последующем вызове функции, пока не будет
достигнут некоторый базисный вариант (иначе рекурсия
будет бесконечной).
3

4. Пример: вычисление факториала

Рекурсивный алгоритм часто строится на основе некоторой
рекуррентной последовательности. Например, для расчета
n! можно использовать эквивалентные соотношения:
Но способы использования рекуррентного соотношения
могут различаться.
4

5. Пример: вычисление факториала

Рекуррентные вычисления – это вычисления «снизу-вверх»
на
основе
циклов,
от
начальных
членов
последовательности к следующим (итерационный процесс)
(1! -> 2! -> 3! ->…-> (n-1)! -> n!)
int facti(int n)
{
int F = 1, i;
if (n <= 0) return 1;
for (i = 1; i <= n; i++)
F *= i;
return F;
}
5

6. Пример: вычисление факториала

Рекурсивные вычисления проводятся «сверху-вниз»:
делается попытка вычислить конечное значение через
предыдущие (рекурсивный спуск), и продолжить этот
процесс, пока не будут получены известные начальные
значения последовательности (базисный вариант). После
этого начинается обратный процесс – функция возвращает
управление и вычисленное значение в точку своего вызова
(рекурсивный подъем).
int factr(int n)
{
if (n <= 0) return 1; // базисный вариант
else return factr(n-1) * n;// рекурсивный спуск
}
void main(…)
{ cout << factr(3); }
6

7. Пример: вычисление факториала

При каждом новом вызове рекурсивной функции в стеке
выделяется память для хранения параметров, локальных
переменных и возвращаемого значения. При этом
вызывающая функция еще не завершила свою работу,
поэтому выделенная для нее память не освобождается.
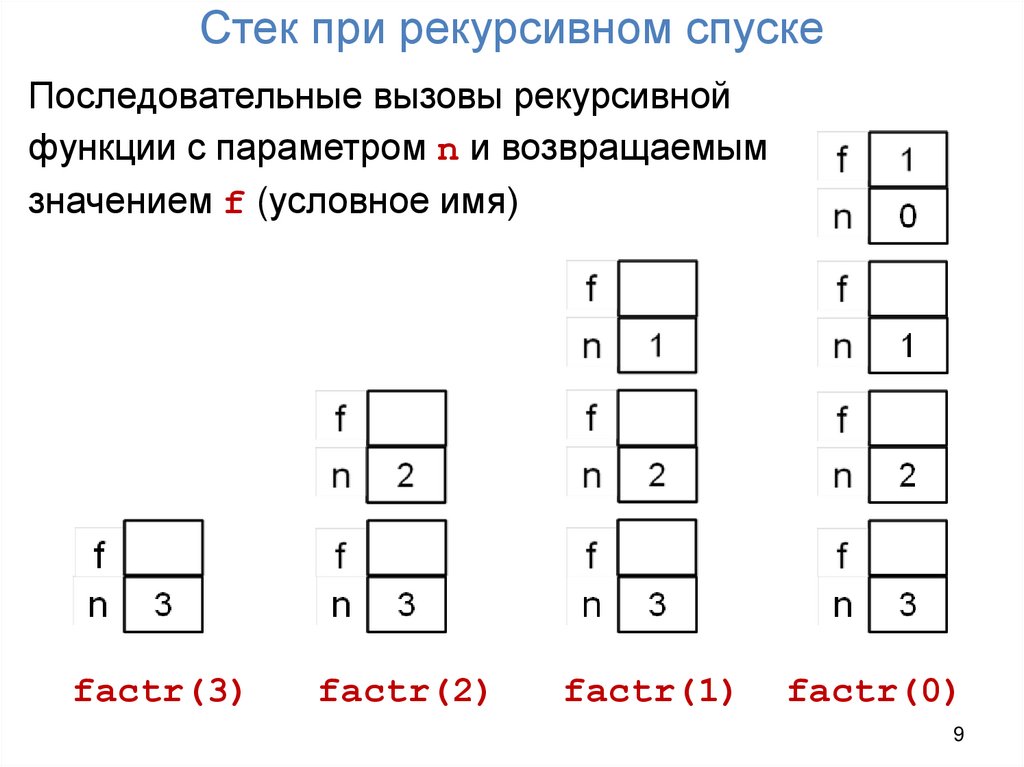
Например, при вызове factr(2) в стеке выделяется
память для параметра n=2 и возвращаемого значения. Но в
это время еще не завершено выполнение factr(3),
поэтому ранее выделенная память для n=3 и
возвращаемого значения не освобождается.
7

8. Пример: вычисление факториала

При вызове fact(0) возвращаемое значение 1
вычисляется непосредственно, поэтому рекурсивный спуск
завершается.
Количество вложенных вызовов
называется глубиной рекурсии.
рекурсивной
функции
Глубина рекурсии определяет не только трудоемкость
алгоритма, но и затраты памяти на его выполнение.
В нашем примере глубина рекурсии равна 4.
8

9. Стек при рекурсивном спуске

Последовательные вызовы рекурсивной
функции с параметром n и возвращаемым
значением f (условное имя)
factr(3)
factr(2)
factr(1)
factr(0)
9

10. Пример: вычисление факториала

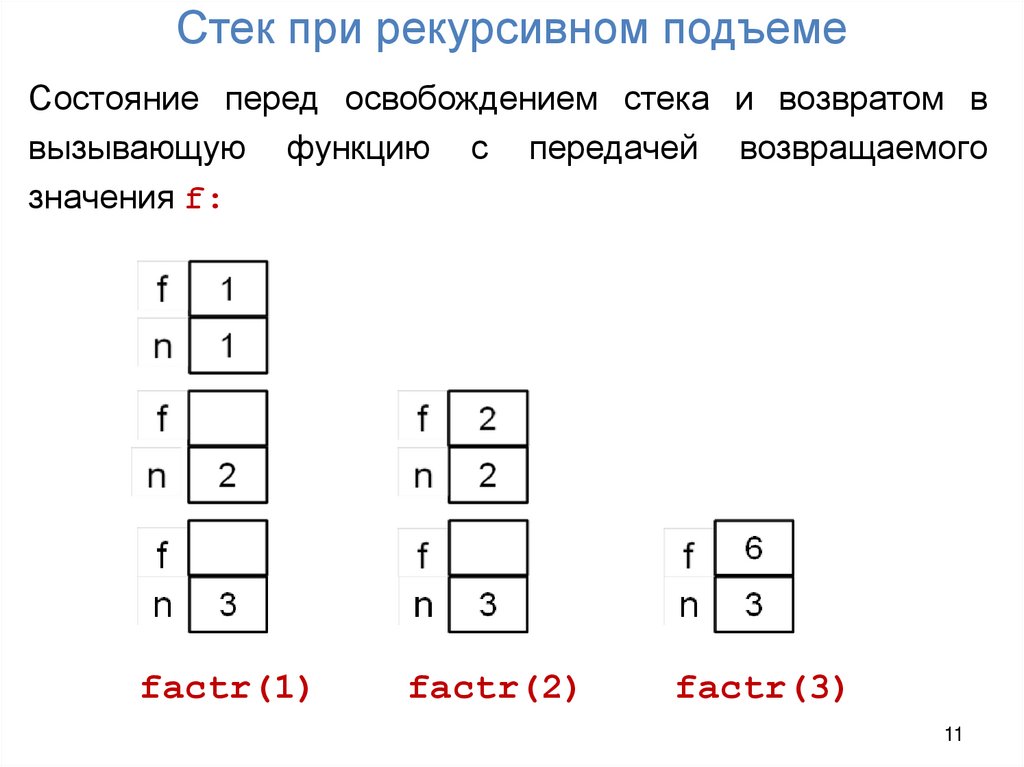
factr(0) возвращает в вызывающую функцию factr(1)
значение 1, которое умножается на текущее n=1, и
формируется новое возвращаемое значение f=1. После
этого участок стека, выделенный для factr(1),
освобождается с передачей возвращаемого значения в
factr(2).
Процесс продолжается, пока factr(3) не сформирует и не
передаст в функцию main значение 3!=6.
10

11. Стек при рекурсивном подъеме

Состояние перед освобождением стека и возвратом в
вызывающую функцию с передачей возвращаемого
значения f:
factr(1)
factr(2)
factr(3)
11

12. Метод математической индукции

Метод математической индукции используется для
доказательства некоторых утверждений и исследования
работы циклов и рекурсивных функций. Он включает 3
основных этапа:
1) базис, 2) предположение, 3) индуктивный вывод.
На
этапе
базиса
проверяют,
что
доказываемое
утверждение P(n) относительно параметра индукции n
справедливо при n = n0.
12
12

13. Метод математической индукции

На
втором
этапе
делается
предположение,
что
утверждение P(n) справедливо для всех значений n,
не бóльших, чем некоторое k, k ≥ n ≥ n0.
На этапе индуктивного вывода доказывается, что P(n)
будет справедливо при n = k + 1 > n0. Из этого следует,
что утверждение P(n) справедливо для любого n ≥ n0.
13
13

14. Задача «Ханойские башни»

Имеется три колышка:
a, b, c.
расположено n дисков в виде башни.
На колышке
a
Задача: Переложить всю башню на колышек c,
перекладывая по одному диску так, чтобы любой диск
большего размера не лежал на меньшем диске.
14

15. Задача «Ханойские башни»

Решение на основе математической индукции:
Базис. Число дисков n = 1. Переложить диск с колышка
a на колышек c.
Предположение. Пусть алгоритм умеет перекладывать
башни из n = k ≥ 1.
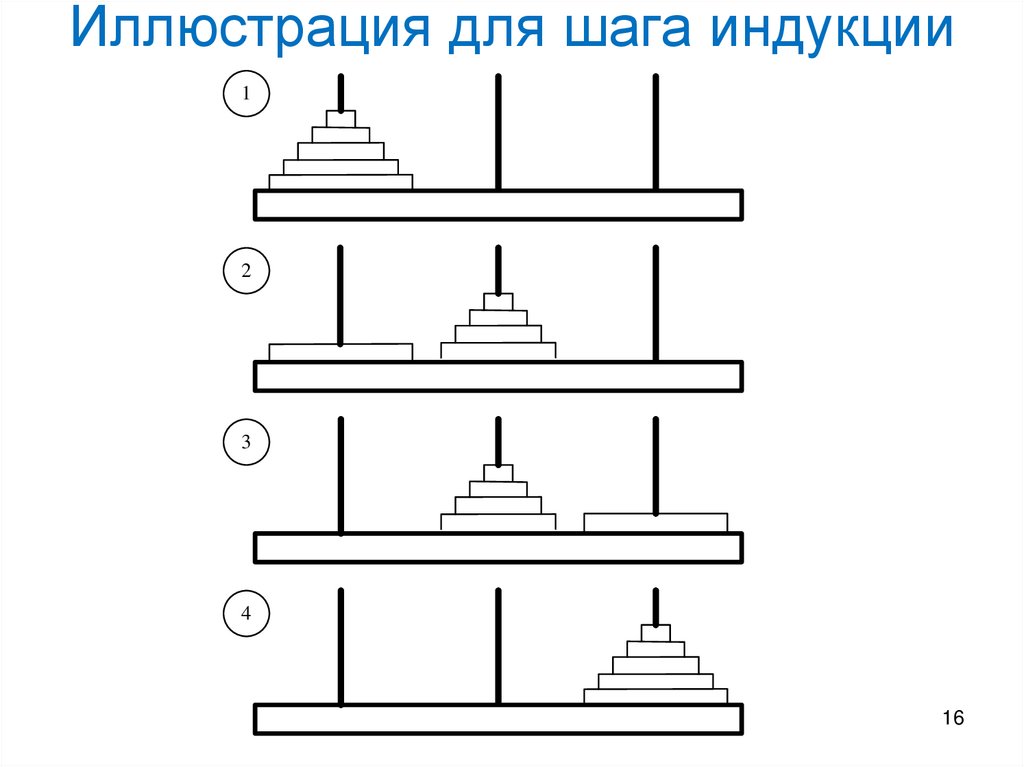
Индукция. Пусть n = k+1 ≥ 2. Перекладываем башню из k
дисков с колышка a на колышек b, затем один диск с
колышка a на колышек c и, наконец, башню из k
дисков с колышка b на колышек c.
15

16. Иллюстрация для шага индукции

1
2
3
4
16

17. Рекурсивная функция

На следующем слайде приводится функция hanoi,
которая выводит порядок перекладывания дисков по
ходам: с какого колышка перекладывается диск и на
какой колышек.
Параметры в заголовке функции hanoi:
• n – число дисков на колышке a
• a – колышек, с которого будут перекладываться диски
• b – промежуточный колышек
• c – колышек, на который будут перекладываться диски
с a.
17

18. Рекурсивная функция

void hanoi(int n, int a, int b, int c)
{
if (n == 1)
cout << a << “->” << c << endl;
else
{
hanoi(n-1, a, c, b);
cout << a << “->” << c << endl;
hanoi(n-1, b, a, c);
}
}
void main(…)
{
hanoi(6, 1, 2, 3);
}
// 6 дисков с 1 на 3
18

19. Рекуррентное соотношение для минимального числа перекладываний

n 1,
1,
H ( n)
2 H (n 1) 1, n 2, 3, ...,
из которого получаем:
H(n) = 2 H(n – 1) + 1 = 22H(n – 2) + 2 + 1 =
2n – 1 + 2n – 2 + … + 2 + 1 = 2n – 1.
Глубина рекурсии: n.
Если на перекладывание одного диска тратить 1
секунду, то при n = 64 всю работу можно завершить
за 264 сек ≈ 580 млрд. лет.
19

20. Рекурсивное вычисление чисел Фибоначчи

int fib(int n)
{
if (!n) return 0;
else if (n == 1) return 1;
else return fib(n-1) + fib(n-2);
}
Количество рекурсивных вызовов
числами Фибоначчи Fn :
Rn
и их связь с
R0 1, R1 1,
Rn Rn 1 Rn 2 1, n 2, 3, ...
Rn : 1, 1, 3, 5, 9, 15, 25, 41, 67,...
Fn : 0, 1, 1, 2, 3, 5, 8, 13, 21,...
Rn = 2Fn+1 – 1
20

21. Рекурсивный алгоритм с массивом

int F[50];
int fib(int n)
{
if (!n) return F[0] = 0;
else if (n == 1) return F[1] = 1;
else if (F[n] > 0) return F[n];
else return F[n] = fib(n-1) + fib(n-2);
}
void main(…)
{
int i, n; cin >> n;
for (i = 0; i < n; i++) F[i] = 0;
cout << fib(n);
}
21