ЛЕКЦИЯ 2 - Методы и свойства проецирования Эпюр точки

1.

Методы проекций. Эпюр Монжа. Чертеж точки,
прямой и плоскости на эпюре.
Сениор-лектор Жаркимбаева Гульнара Бахитовна

2.

Введение. Методы и свойства проецирования
Как любая наука «Начертательная геометрия» изучает объективные законы природы. С ее помощью познаются
геометрические свойства предметов реального мира, характеризуемые понятиями «форма», «размеры», «положение
в пространстве», «взаимное положение». Методы начертательной геометрии являются теоретической базой для
решения задач технического черчения.
Гаспар Монж
В технике чертежи являются основным средством выражения человеческих идей.
Они должны не только определять форму и размеры предметов, но и быть достаточно
простыми и точными в графическом исполнении, помогать всесторонне исследовать
предметы и их отдельные детали. Для того чтобы правильно выразить свои мысли с
помощью рисунка, эскиза, чертежа требуется знание теоретических основ построения
изображений геометрических объектов, их многообразие и отношения между ними, что и
составляет предмет начертательной геометрии.
Изучение начертательной геометрии способствует развитию пространственного
воображения и навыков правильного логического мышления, совершенствуя нашу
способность – по плоскому изображению мысленно создавать представления о форме
предмета и наоборот – создавать изображения мысленно созданных образов –
визуализация мысли.
Зарождение начертательной геометрии связывается с именем Гаспара Монжа –
французского математика, геометра (1746–1818), опубликовавшего в 1798 году книгу
«Начертательная геометрия», в которой были сформулированы основные принципы
комплексного проецирования.

3.

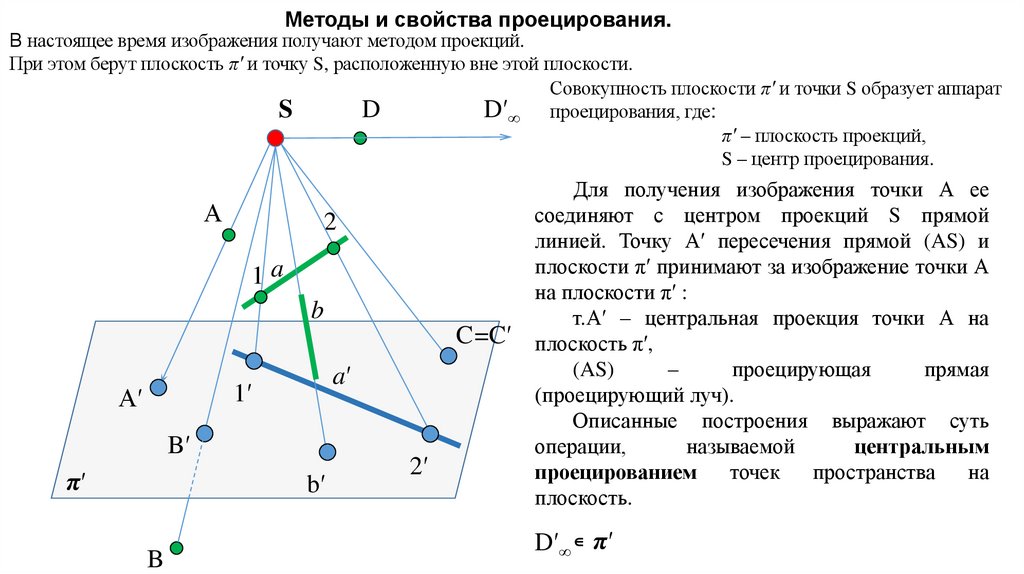
Методы и свойства проецирования.
В настоящее время изображения получают методом проекций.
При этом берут плоскость π′ и точку S, расположенную вне этой плоскости.
Совокупность плоскости π′ и точки S образует аппарат
S
D′∞ проецирования, где:
D
π′ – плоскость проекций,
S – центр проецирования.
А
2
1a
b
C=C′
А′
a′
1′
B′
π′
b′
B
2′
Для получения изображения точки А ее
соединяют с центром проекций S прямой
линией. Точку А′ пересечения прямой (AS) и
плоскости π′ принимают за изображение точки А
на плоскости π′ :
т.А′ – центральная проекция точки А на
плоскость π′,
(AS)
–
проецирующая
прямая
(проецирующий луч).
Описанные построения выражают суть
операции,
называемой
центральным
проецированием
точек
пространства
на
плоскость.
D′∞ π′

4.

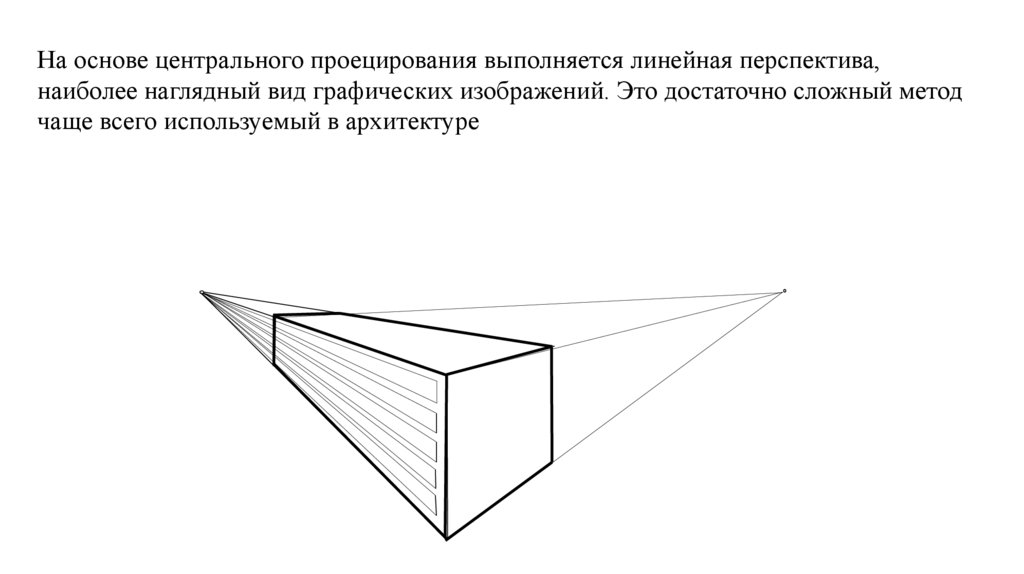
На основе центрального проецирования выполняется линейная перспектива,
наиболее наглядный вид графических изображений. Это достаточно сложный метод
чаще всего используемый в архитектуре

5.

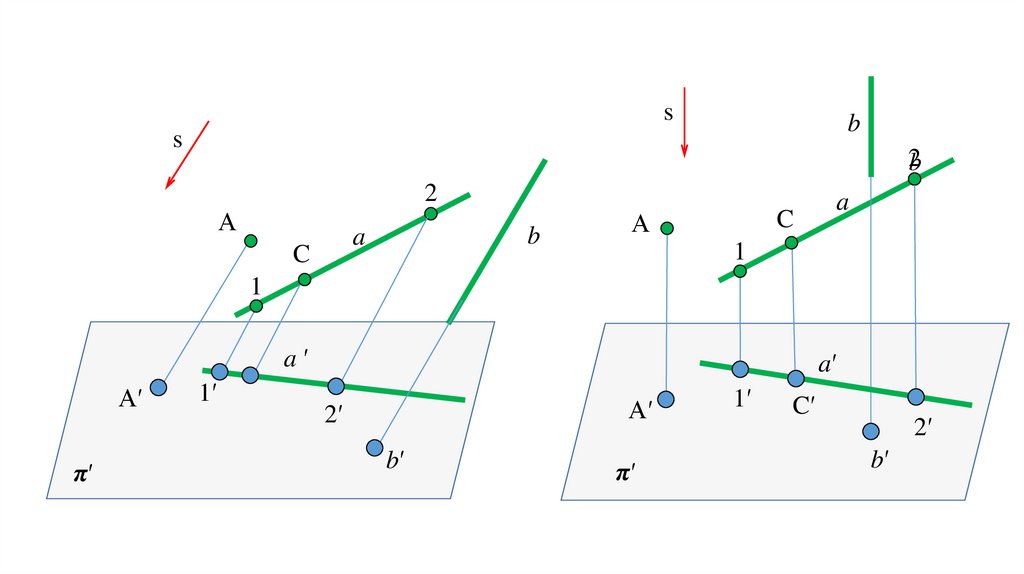
Параллельное проецирование является частным случаем центрального проецирования. При этом методе
полагается, что центр проецирования S удален в бесконечность (бесконечно удаленная точка S∞), в результате
чего проецирующие лучи становятся взаимно параллельными, и проецирование всех точек осуществляется по
единому направлению s. В зависимости от угла, под которым проецирующий луч падает на плоскость проекций
различают проекции:
1. прямоугольные, или ортогональные (при угле, равном 900),
2. косоугольные (при угле, не равном 900).

6.

s
b
s
2b
2
А
b
a
C
А
C
a
1
1
a′
А′
π′
1′
a′
А′
2′
b′
π′
1′
C′
2′
b′

7.

Центральные и параллельные
проекции имеют ряд общих
геометрических свойств:
s
• Точка проецируется в точку, прямая – в прямую
(за исключением проецирующей прямой, проекция
которой вырождается в точку), плоская фигура – в
плоскую фигуру (за исключением того случая, когда
эта
фигура
является
проецирующей
и
отображается в виде отрезка прямой), объемные
тела проецируются в плоскую фигуру.
• Свойство принадлежности. В обоих видах
проекций
сохраняется
взаимная
принадлежность геометрических элементов:
если точка принадлежит прямой, то проекция
этой точки принадлежит проекции этой прямой
( C a) ( C’ a’ )
b
2b
А
C
a
1
a′
А′
π′
1′
C′
2′
b′

8.

b
а
b’
а
’
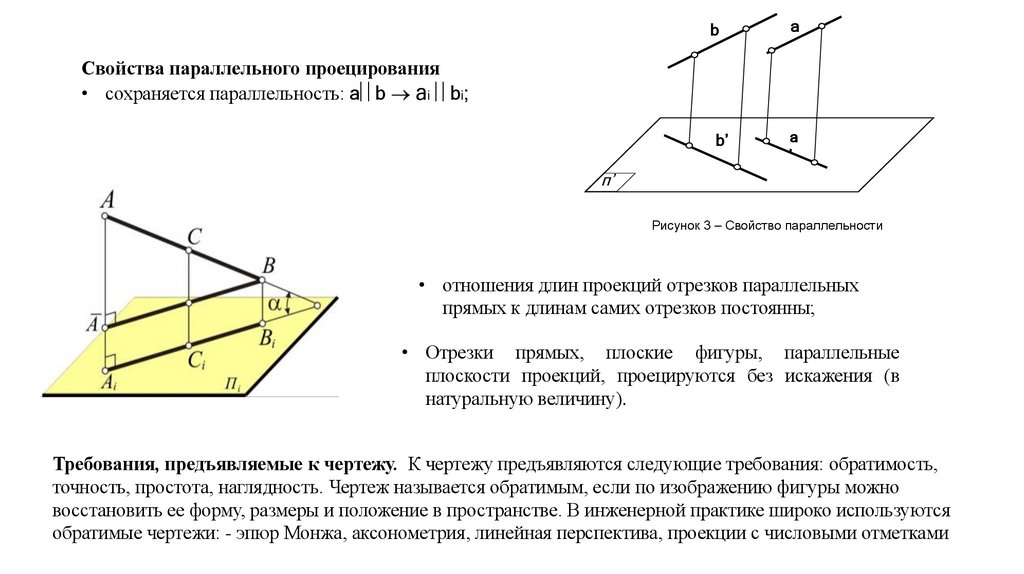
Свойства параллельного проецирования
• сохраняется параллельность: а b аi bi;
π’
Рисунок 3 – Свойство параллельности
• отношения длин проекций отрезков параллельных
прямых к длинам самих отрезков постоянны;
• Отрезки прямых, плоские фигуры, параллельные
плоскости проекций, проецируются без искажения (в
натуральную величину).
Требования, предъявляемые к чертежу. К чертежу предъявляются следующие требования: обратимость,
точность, простота, наглядность. Чертеж называется обратимым, если по изображению фигуры можно
восстановить ее форму, размеры и положение в пространстве. В инженерной практике широко используются
обратимые чертежи: - эпюр Монжа, аксонометрия, линейная перспектива, проекции с числовыми отметками

9.

Эпюр Монжа
Гаспар Монж

10.

• Эпюр Монжа – основной вид обратимого изображения. Французский
математик и инженер Гаспар Монж (1746-1818гг.), систематизировав и
обобщив накопленные к тому времени знания по теории и практике
построения изображений предметов пространства, предложил получать их
изображения путем прямоугольного проецирования на две или три
взаимно перпендикулярные плоскости проекций. В зависимости от этого
также чертежи называют двухкартинными или трехкартинными.
Совокупность двух или более взаимосвязанных ортогональных проекций
предмета, расположенных на одной плоскости, называют комплексным
чертежом (или ЭПЮРОМ МОНЖА).
Чертеж называется обратимым, если по изображению фигуры можно
восстановить ее форму, размеры и положение в пространстве. В инженерной
практике широко используются обратимые чертежи: - эпюр Монжа,
аксонометрия, линейная перспектива, проекции с числовыми отметками.

11.

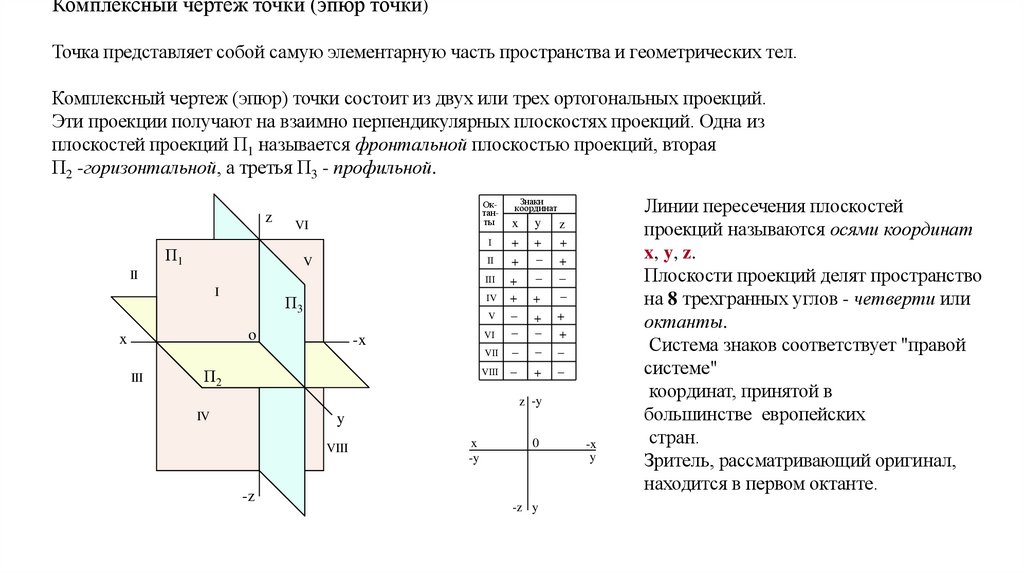
Комплексный чертеж точки (эпюр точки)
Точка представляет собой самую элементарную часть пространства и геометрических тел.
Комплексный чертеж (эпюр) точки состоит из двух или трех ортогональных проекций.
Эти проекции получают на взаимно перпендикулярных плоскостях проекций. Одна из
плоскостей проекций П1 называется фронтальной плоскостью проекций, вторая
П2 -горизонтальной, а третья П3 - профильной.
z
Октанты
VI
I
П1
V
II
II
III
I
П3
III
+
_
_
_
VIII
_
+
VI
П2
+
+
_
_
y
VII
V
-x
x
+
+
+
+
_
_
IV
o
x
Знаки
координат
z
+
+
_
_
+
+
_
_
z -y
IV
y
VIII
-z
x
-y
0
-z y
-x
y
Линии пересечения плоскостей
проекций называются осями координат
x, y, z.
Плоскости проекций делят пространство
на 8 трехгранных углов - четверти или
октанты.
Система знаков соответствует "правой
системе"
координат, принятой в
большинстве европейских
стран.
Зритель, рассматривающий оригинал,
находится в первом октанте.

12.

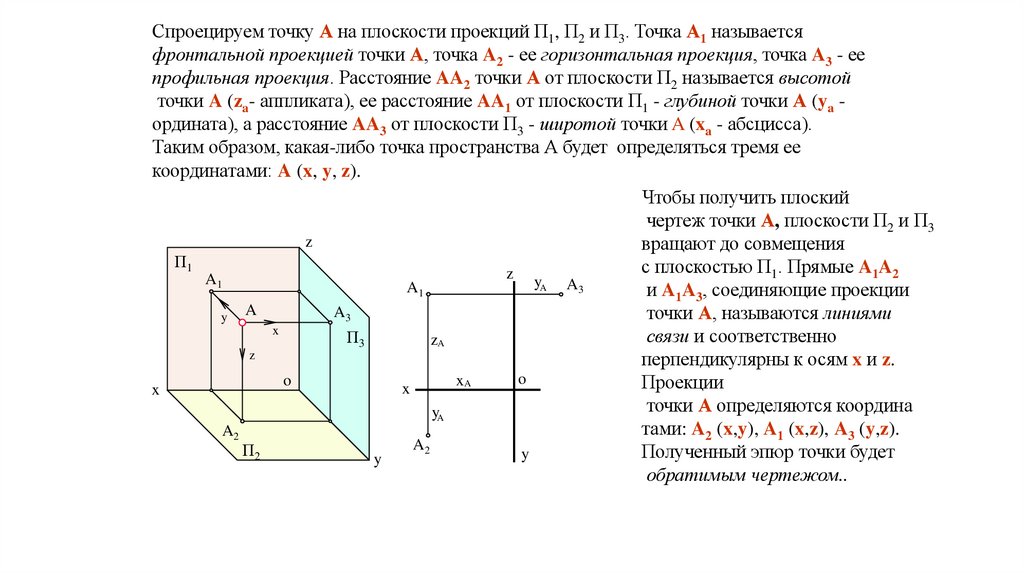
Спроецируем точку А на плоскости проекций П1, П2 и П3. Точка А1 называется
фронтальной проекцией точки А, точка A2 - ее горизонтальная проекция, точка A3 - ее
профильная проекция. Расстояние AA2 точки А от плоскости П2 называется высотой
точки A (za- аппликата), ее расстояние AA1 от плоскости П1 - глубиной точки А (ya ордината), а расстояние AA3 от плоскости П3 - широтой точки A (xa - абсцисса).
Таким образом, какая-либо точка пространства А будет определяться тремя ее
координатами: A (x, y, z).
Чтобы получить плоский
чертеж точки А, плоскости П2 и П3
z
вращают до совмещения
П1
с плоскостью П1. Прямые A1A2
z
A1
y
A3
A
A1
и A1A3, соединяющие проекции
A3
точки А, называются линиями
y A
x
связи и соответственно
П3
zA
z
перпендикулярны к осям x и z.
o
xA
o
Проекции
x
x
точки А определяются координа
yA
тами: A2 (x,y), A1 (x,z), A3 (y,z).
A2
A
2
П2
Полученный эпюр точки будет
y
y
обратимым чертежом..

13.

z
z
p1
p3
p1
A1
A3
AZ
A1
Az
A3
o
Ay
p3
A
A3
x
o
Ax
Ax
x
y
Ay
p2
A2
A2
y
A2
Ay
p2
y

14.

z
z
p1
A1
A1
A3
o
Ay
AZ
p3
A
x
A3
x
Az
Ax
Ax
Ay
A2
z
p2
Ay
A2
y
Az
A1
A3
y
x
o
Ax
A2
Ay
y
Ay
y
y

15.

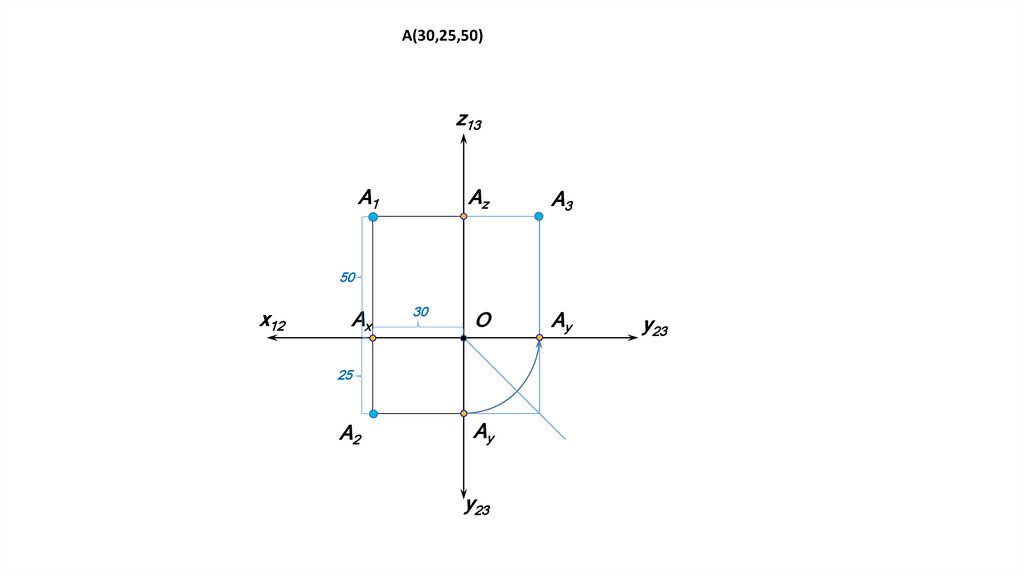
А(30,25,50)
z13
A1
Az
A3
О
Ay
50
x12
Ax
30
25
A2
Ay
y23
y23

16.

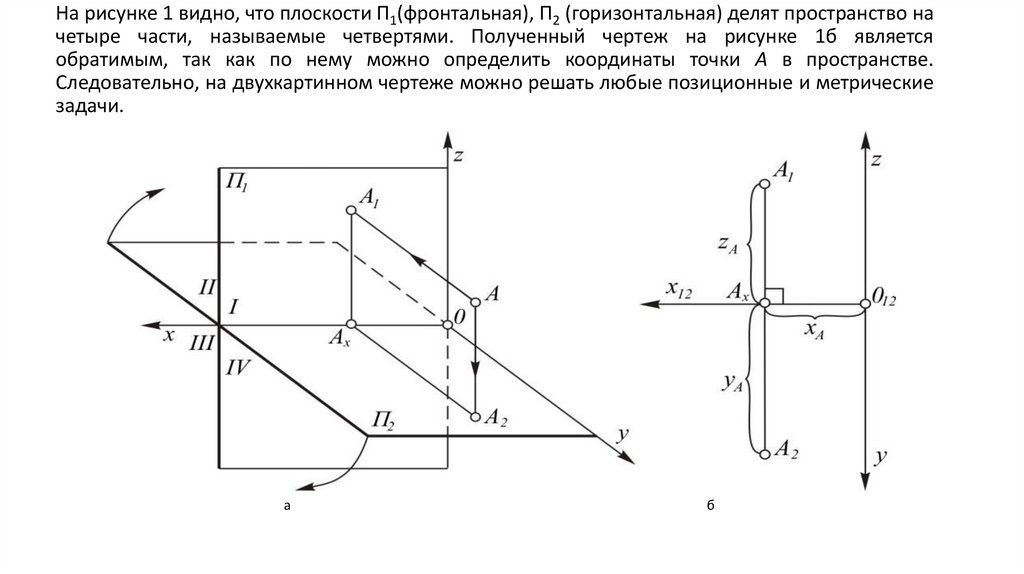
На рисунке 1 видно, что плоскости П1(фронтальная), П2 (горизонтальная) делят пространство на
четыре части, называемые четвертями. Полученный чертеж на рисунке 1б является
обратимым, так как по нему можно определить координаты точки А в пространстве.
Следовательно, на двухкартинном чертеже можно решать любые позиционные и метрические
задачи.
а
б

17.

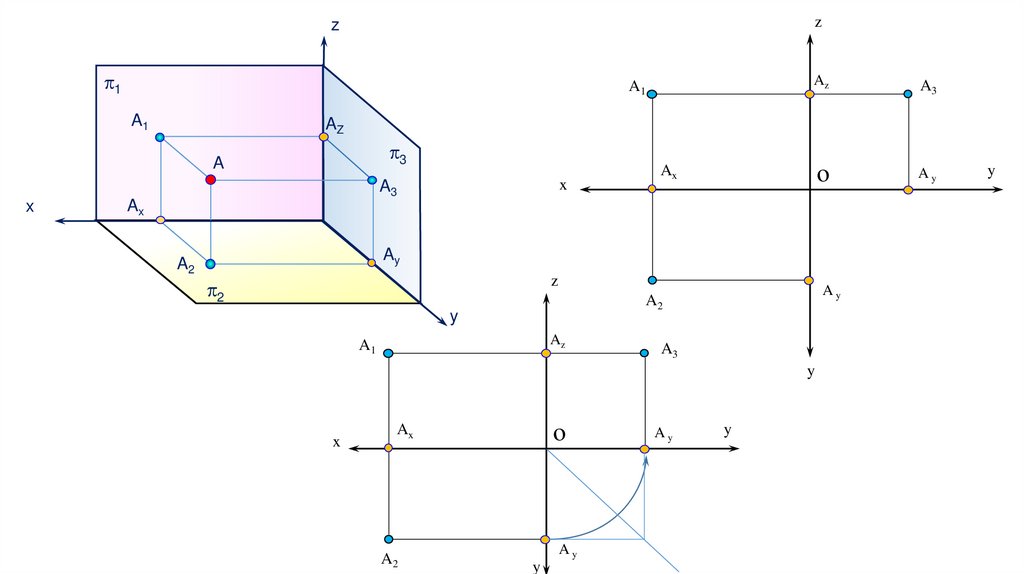
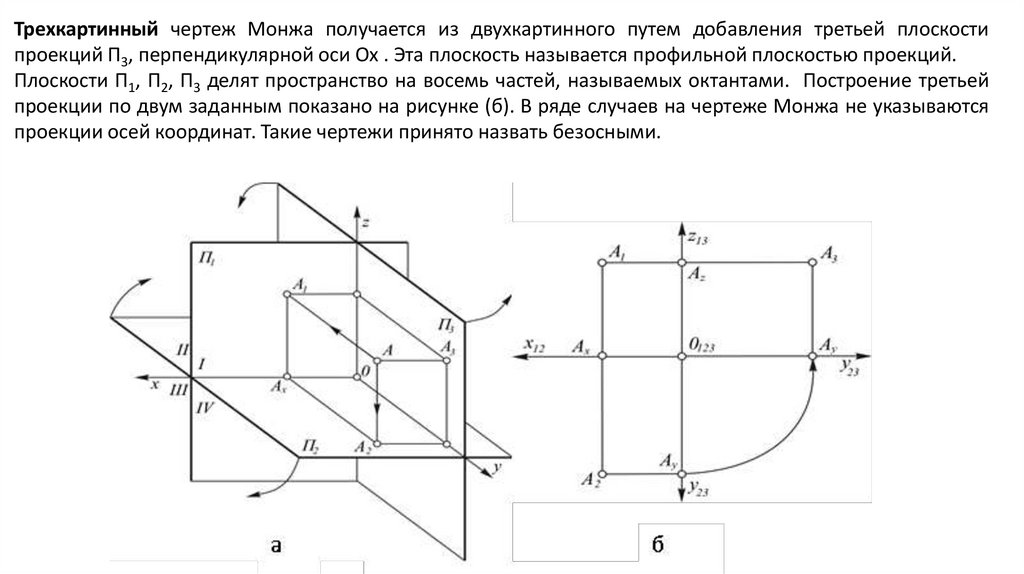
Трехкартинный чертеж Монжа получается из двухкартинного путем добавления третьей плоскости
проекций П3, перпендикулярной оси Оx . Эта плоскость называется профильной плоскостью проекций.
Плоскости П1, П2, П3 делят пространство на восемь частей, называемых октантами. Построение третьей
проекции по двум заданным показано на рисунке (б). В ряде случаев на чертеже Монжа не указываются
проекции осей координат. Такие чертежи принято назвать безосными.

18.

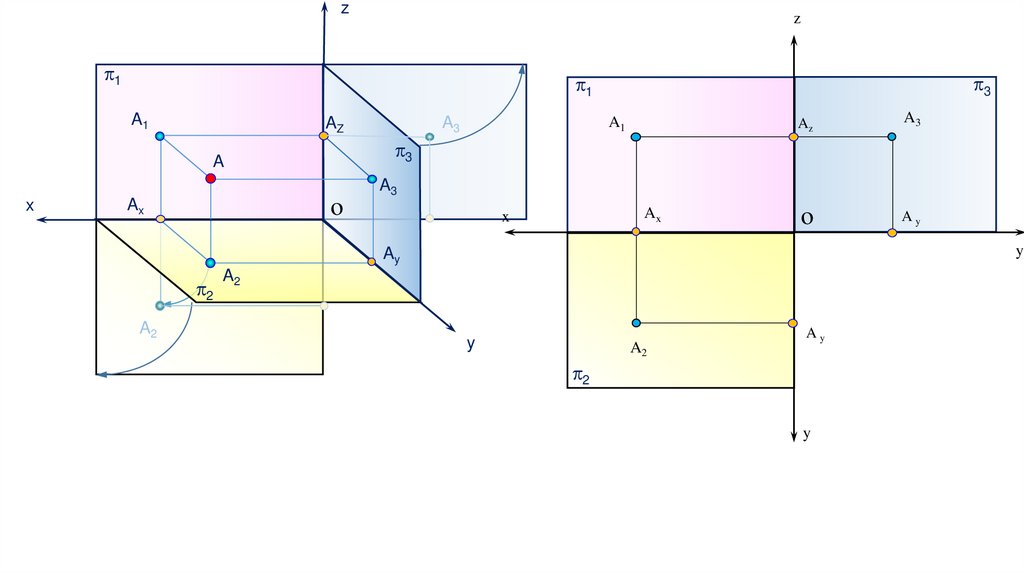
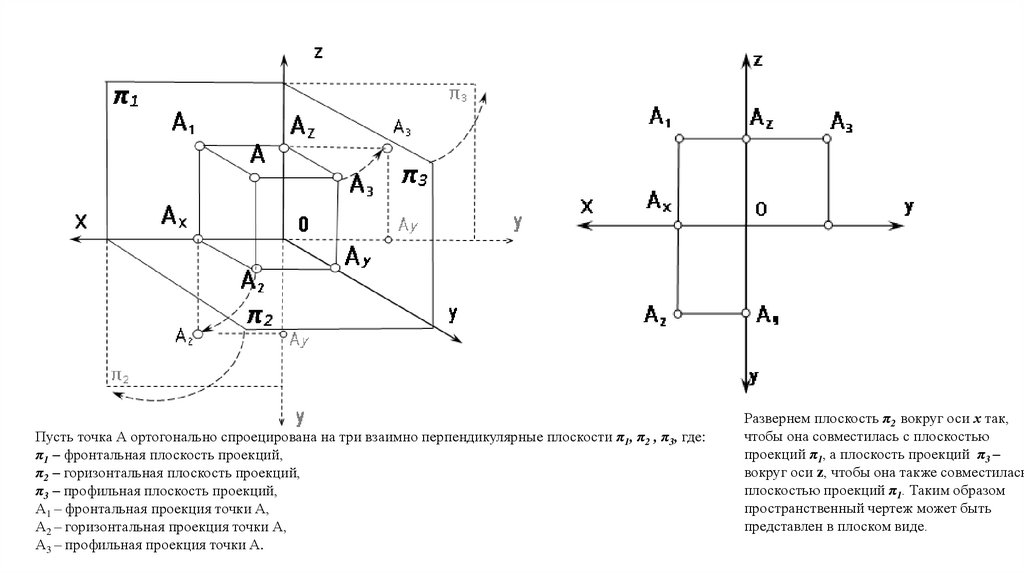
Пусть точка А ортогонально спроецирована на три взаимно перпендикулярные плоскости π1, π2 , π3, где:
π1 – фронтальная плоскость проекций,
π2 – горизонтальная плоскость проекций,
π3 – профильная плоскость проекций,
А1 – фронтальная проекция точки А,
А2 – горизонтальная проекция точки А,
А3 – профильная проекция точки А.
Развернем плоскость π2 вокруг оси х так,
чтобы она совместилась с плоскостью
проекций π1, а плоскость проекций π3 –
вокруг оси z, чтобы она также совместилась
плоскостью проекций π1. Таким образом
пространственный чертеж может быть
представлен в плоском виде.

19.

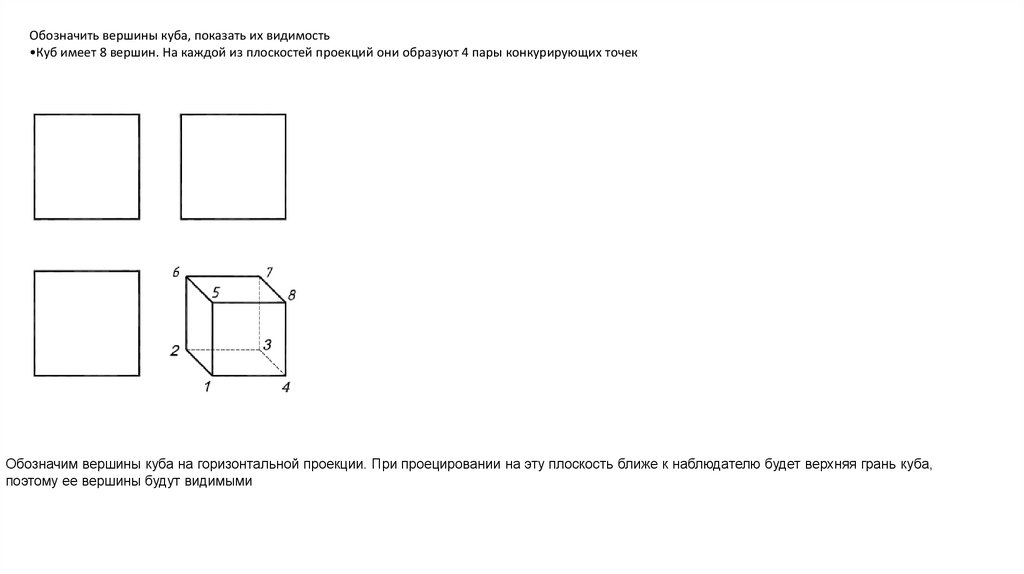
Обозначить вершины куба, показать их видимость
•Куб имеет 8 вершин. На каждой из плоскостей проекций они образуют 4 пары конкурирующих точек
Обозначим вершины куба на горизонтальной проекции. При проецировании на эту плоскость ближе к наблюдателю будет верхняя грань куба,
поэтому ее вершины будут видимыми

20.

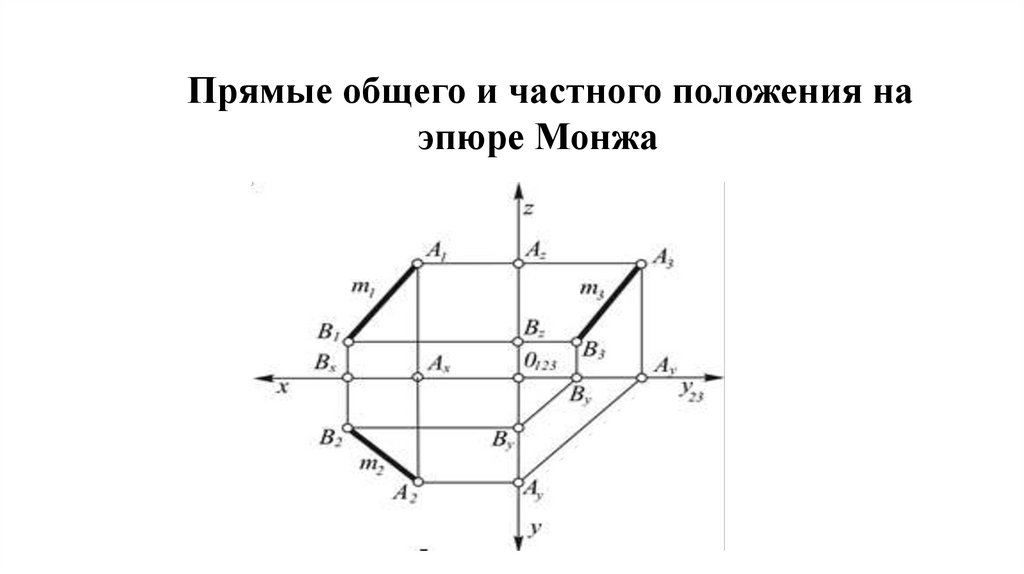
Прямые общего и частного положения на
эпюре Монжа

21.

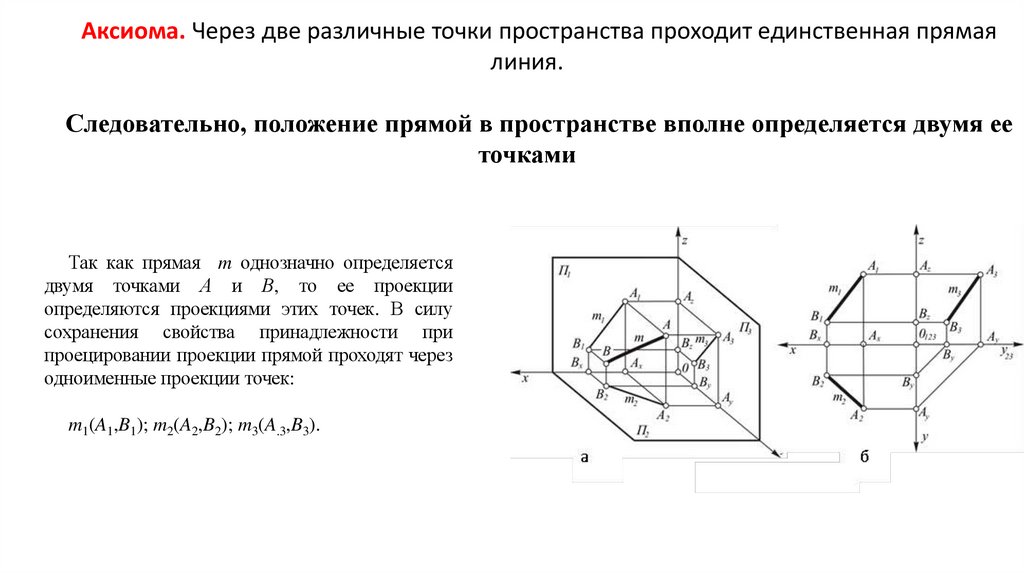
Аксиома. Через две различные точки пространства проходит единственная прямая
линия.
Следовательно, положение прямой в пространстве вполне определяется двумя ее
точками
Так как прямая m однозначно определяется
двумя точками А и В, то ее проекции
определяются проекциями этих точек. В силу
сохранения свойства принадлежности при
проецировании проекции прямой проходят через
одноименные проекции точек:
m1(A1,B1); m2(A2,B2); m3(A.3,B3).

22.

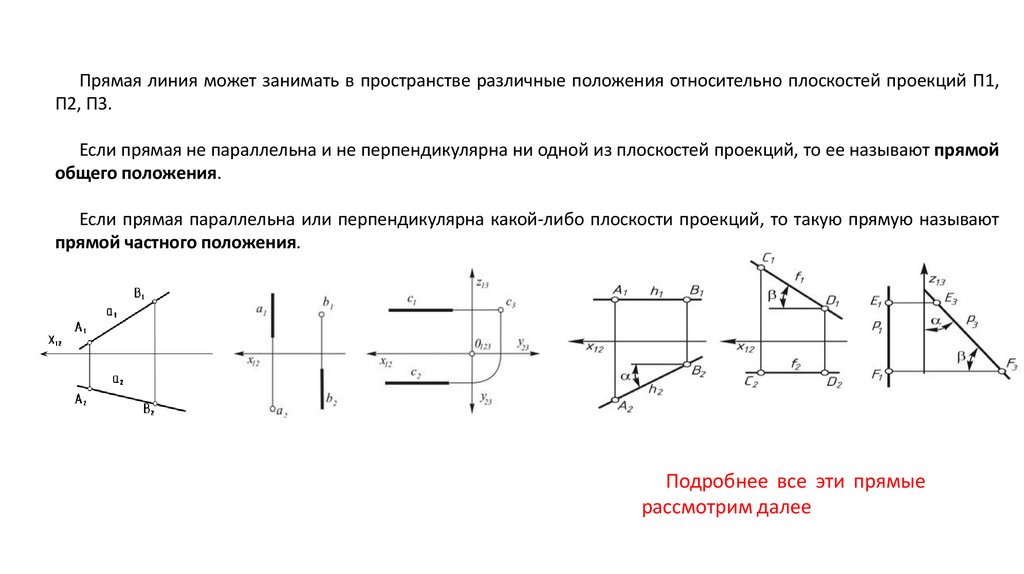
Прямая линия может занимать в пространстве различные положения относительно плоскостей проекций Π1,
Π2, Π3.
Если прямая не параллельна и не перпендикулярна ни одной из плоскостей проекций, то ее называют прямой
общего положения.
Если прямая параллельна или перпендикулярна какой-либо плоскости проекций, то такую прямую называют
прямой частного положения.
Подробнее все эти прямые
рассмотрим далее

23.

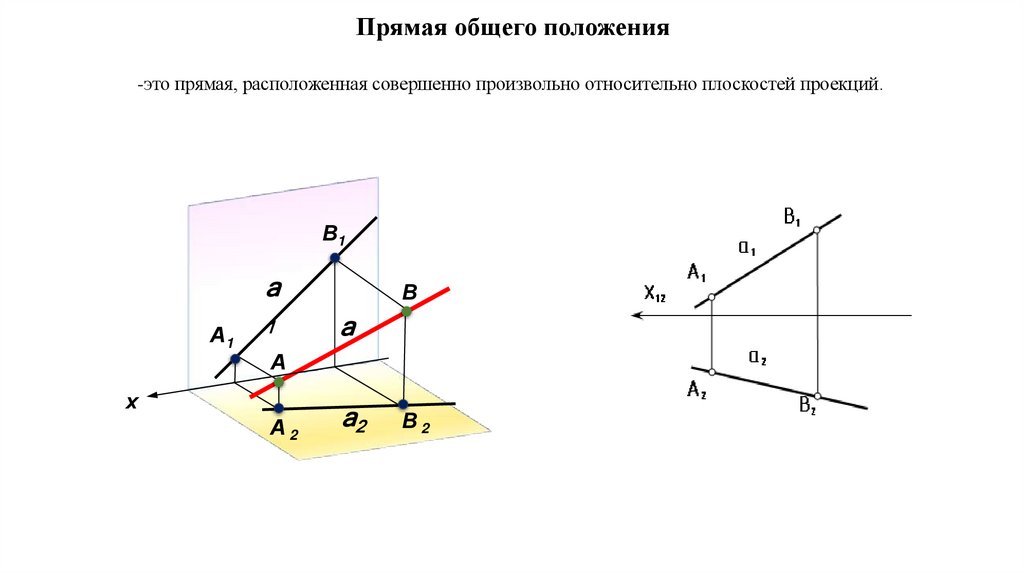
Прямая общего положения
-это прямая, расположенная совершенно произвольно относительно плоскостей проекций.
В1
а
А1
1
В
а
А
х
А2
а2
В2

24.

Прямые уровня
– это прямые, параллельные плоскостям проекций.
a) Горизонтальная прямая (Горизонталь) – h – это прямая, параллельная горизонтальной плоскости проекций π2.
Все точки прямой находятся на одинаковом расстоянии от плоскости π2;
b) Фронтальная прямая (Фронталь) – f – это прямая, параллельная фронтальной плоскости проекций π1. Все
точки прямой находятся на одинаковом расстоянии от плоскости π1;
c) Профильная прямая – р – это прямая, параллельная профильной плоскости проекций π3. Все точки прямой
находятся на одинаковом расстоянии от плоскости π3.
AB A2 B2
CD C1D1
EF E3 F3
h,p 1
f ,p 2
p,p 1
p,p 2

25.

Горизонтальная прямая (Горизонталь) – h
z
p1
A1
h1
B1
B
A
X
Ax
Bx
A2
h,p 1
B3
p3
A3
AB A2 B2
AZ=BZ
By
B2
Ay
p2
y
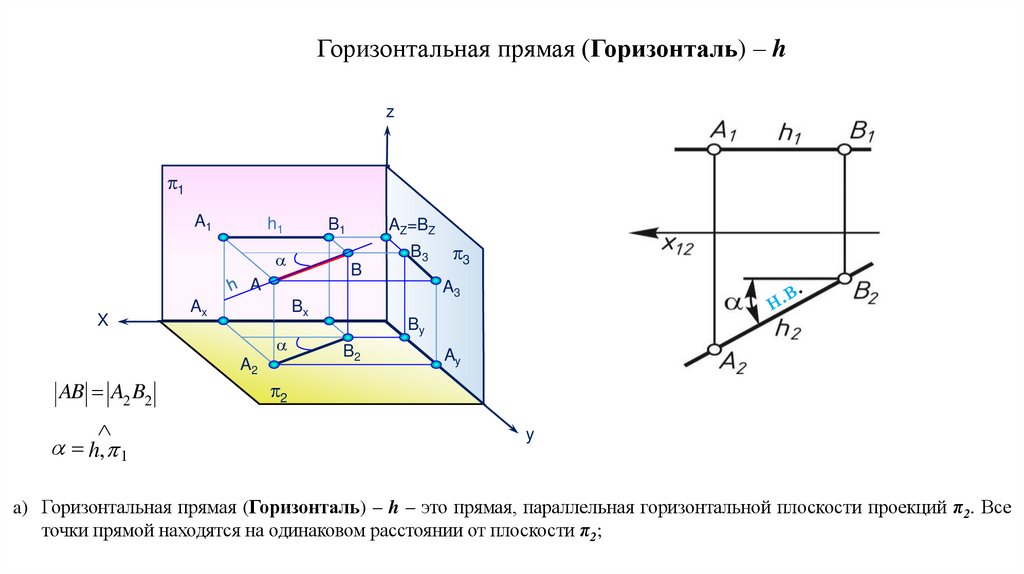
a) Горизонтальная прямая (Горизонталь) – h – это прямая, параллельная горизонтальной плоскости проекций π2. Все
точки прямой находятся на одинаковом расстоянии от плоскости π2;

26.

Фронтальная прямая (Фронталь) – f
B1
П1
A1
f1
А
f
В
х
A2
f2
A1
A2
х
B1
f1
f2
B2
B2
AB A1 B1
f ,p 2
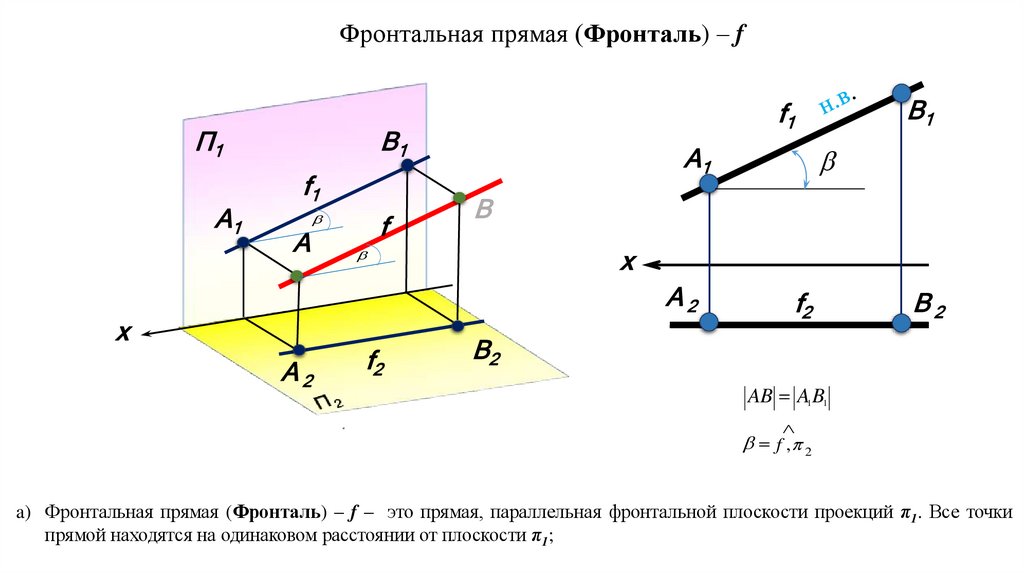
a) Фронтальная прямая (Фронталь) – f – это прямая, параллельная фронтальной плоскости проекций π1. Все точки
прямой находятся на одинаковом расстоянии от плоскости π1;

27.

Профильная прямая – р
П1
B1
B1
B3
В
A1
х
A3
А
A2
A1
х
B2
B3
A3
A2
B2
AB A3 B3
p,p 1
p,p 2
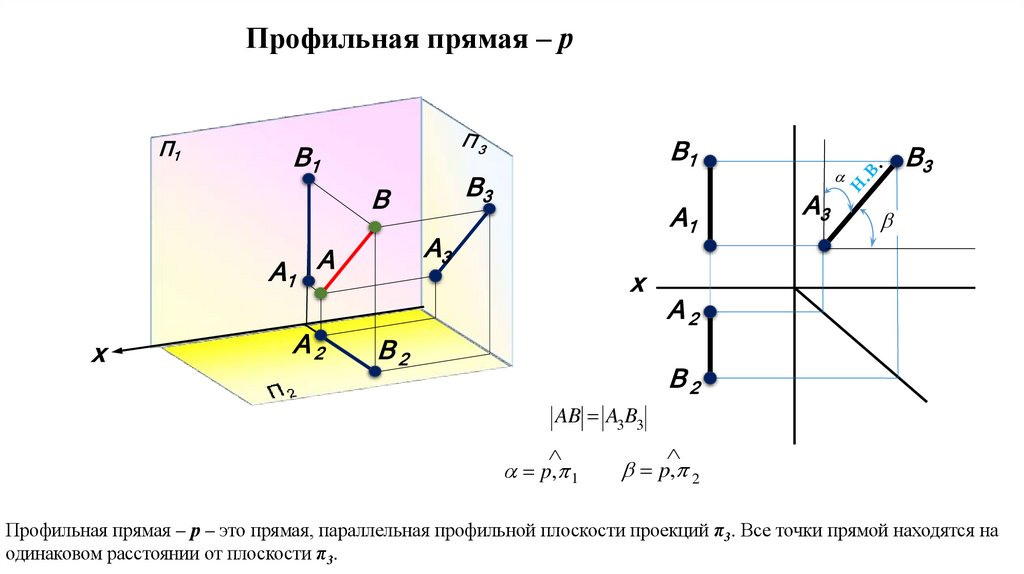
Профильная прямая – р – это прямая, параллельная профильной плоскости проекций π3. Все точки прямой находятся на
одинаковом расстоянии от плоскости π3.

28.

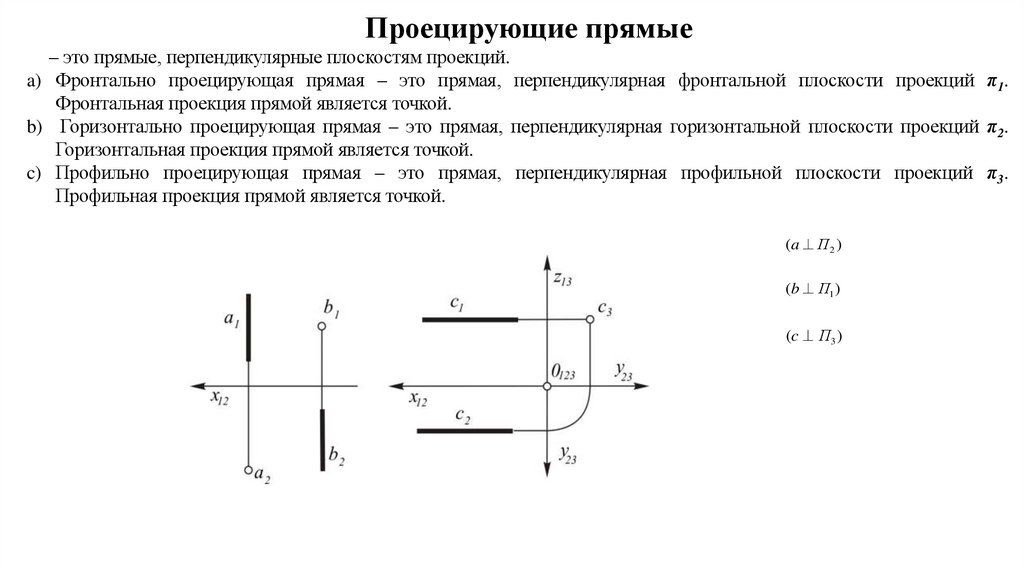
Проецирующие прямые
– это прямые, перпендикулярные плоскостям проекций.
a) Фронтально проецирующая прямая – это прямая, перпендикулярная фронтальной плоскости проекций π1.
Фронтальная проекция прямой является точкой.
b) Горизонтально проецирующая прямая – это прямая, перпендикулярная горизонтальной плоскости проекций π2.
Горизонтальная проекция прямой является точкой.
c) Профильно проецирующая прямая – это прямая, перпендикулярная профильной плоскости проекций π3.
Профильная проекция прямой является точкой.
(a П 2 )
(b П1 )
( c П3 )

29.

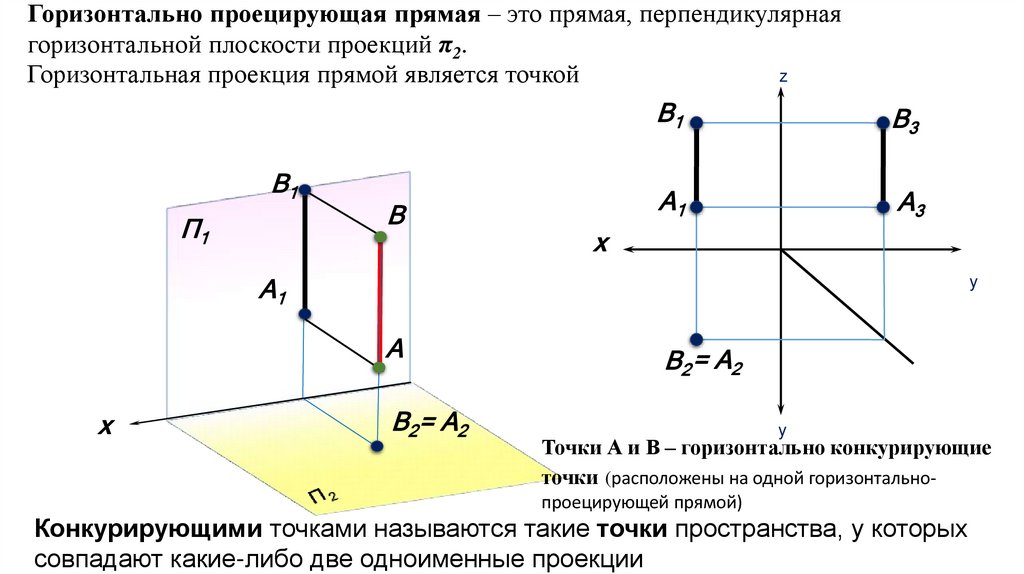
Горизонтально проецирующая прямая – это прямая, перпендикулярная
горизонтальной плоскости проекций π2.
z
Горизонтальная проекция прямой является точкой
B1
П1
В
B1
B3
A1
A3
х
A1
y
А
х
B2 = A2
B2 = A2
y
Точки А и В – горизонтально конкурирующие
точки (расположены на одной горизонтальнопроецирующей прямой)
Конкурирующими точками называются такие точки пространства, у которых
совпадают какие-либо две одноименные проекции

30.

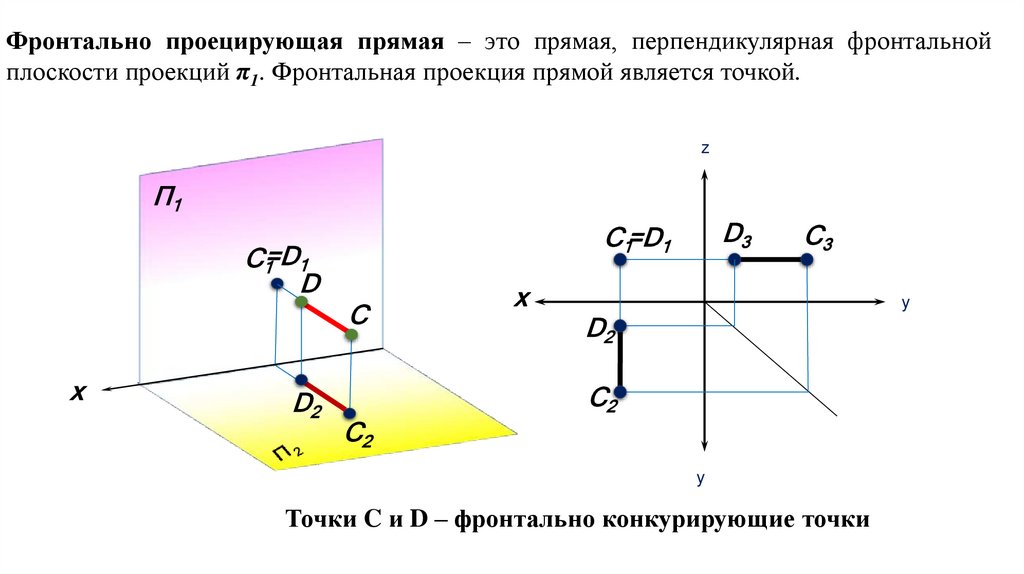
Фронтально проецирующая прямая – это прямая, перпендикулярная фронтальной
плоскости проекций π1. Фронтальная проекция прямой является точкой.
z
П1
C1=D1
D
C
х
D2
D3
C1=D1
C3
х
y
D2
C2
C2
y
Точки C и D – фронтально конкурирующие точки

31.

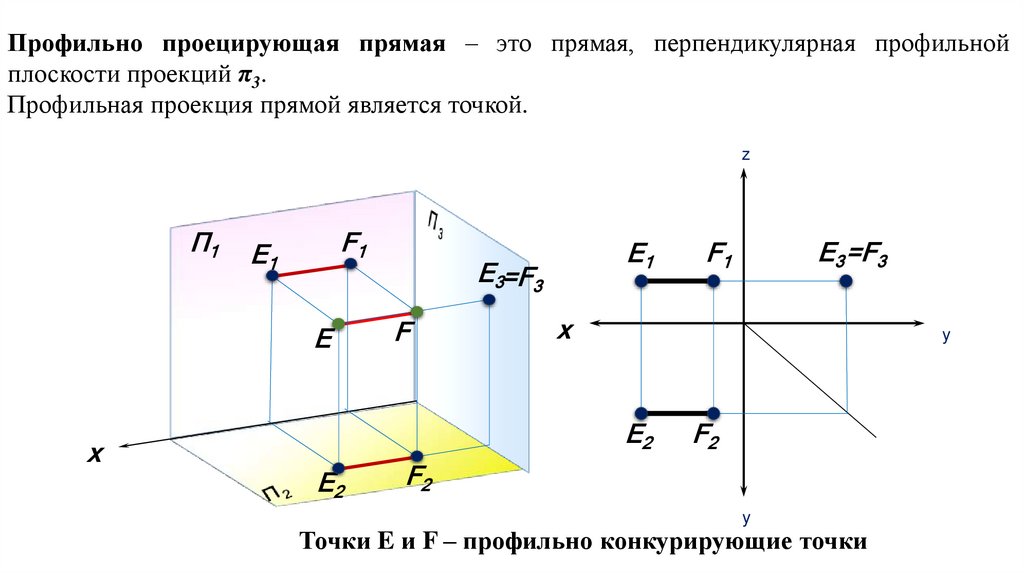
Профильно проецирующая прямая – это прямая, перпендикулярная профильной
плоскости проекций π3.
Профильная проекция прямой является точкой.
z
П1
F1
E1
E
х
E1
E3=F3
F
х
y
E2
E2
E3 =F3
F1
F2
F2
y
Точки E и F – профильно конкурирующие точки

32.

33.

Спасибо за внимание!