Лекция к работе 3

1.

Лекция №4
Рассматриваемые темы:
Тема 8. Методы решения систем линейных алгебраических уравнений (СЛАУ).
Матричный метод.
Тема 9. Метод конечных разностей для численного решения ОДУ второго
порядка.
Тема 10. Основы векторного анализа.
1

2.

Тема 8. Методы решения систем линейных алгебраических
уравнений. Матричный метод.
Определение: система алгебраических уравнений вида
a11 x1 a12 x 2 a13 x3 ... ...a1n x n b1
a 21 x1 a 22 x 2 a 23 x3 ... ...a 2 n x n b2
.
.
.
обозначения:
aij – набор коэффициентов;
xi – неизвестные;
bi – свободные члены.
an1 x1 an 2 x2 an 3 x3 ... ...ann xn bn
называется линейной.
индекс i обозначает строку
aij
индекс j обозначает столбец
2

3.

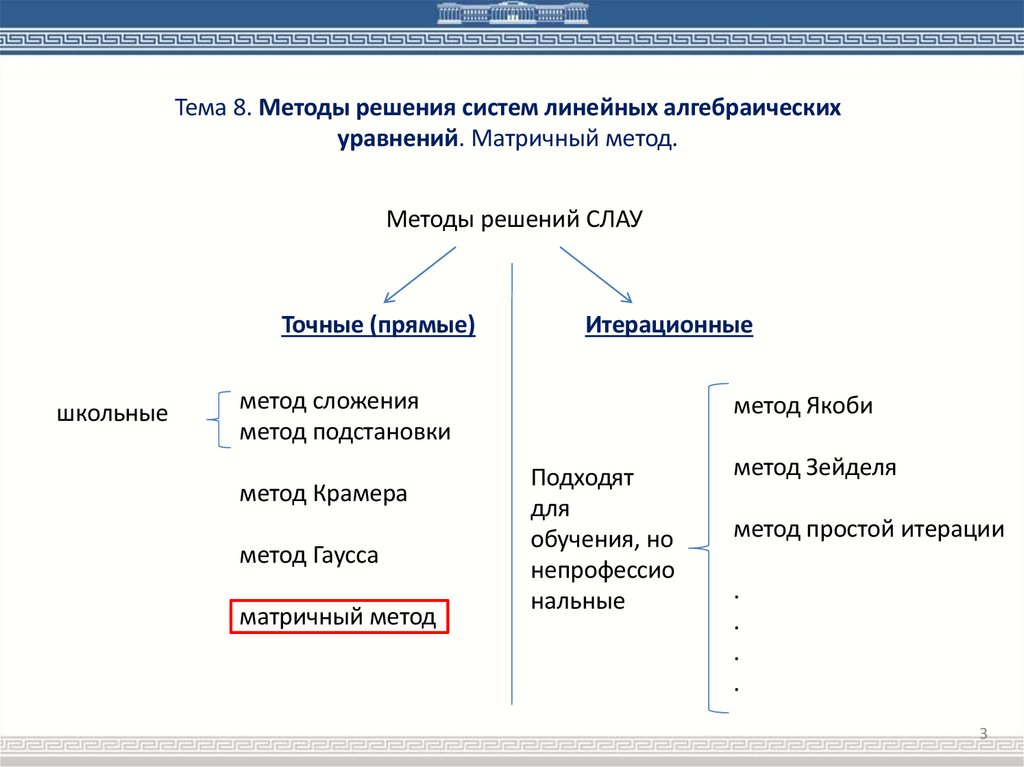
Тема 8. Методы решения систем линейных алгебраических
уравнений. Матричный метод.
Методы решений СЛАУ
Точные (прямые)
школьные
Итерационные
метод сложения
метод подстановки
метод Крамера
метод Гаусса
матричный метод
метод Якоби
Подходят
для
обучения, но
непрофессио
нальные
метод Зейделя
метод простой итерации
.
.
.
.
3

4.

Тема 8. Методы решения систем линейных алгебраических
уравнений. Матричный метод.
Методы решений СЛАУ
Точные
Итерационные
(!) Точные методы решения уравнений позволяют найти решение с
нулевой погрешностью.
(!) Итерационные методы - приближенный методы решения СЛАУ,
позволяет получить значения корней системы с заданной
точностью
4

5.

Тема 8. Методы решения систем линейных алгебраических
уравнений. Матричный метод.
Методы решений СЛАУ
Точные
Пример: дано СЛАУ:
Итерационные
x1 x2 x3 1
2 x1 3 x2 1x3 0
6 x1 x2 3x3 1
Точное решение
-0.75
-0.125
1.875
Итерационное решение
-0.75
-0.125
1.875
погрешность
5

6.

Тема 8. Методы решения систем линейных алгебраических
уравнений. Матричный метод.
Преимущества и недостатки точных и итерационных методов:
1. точные методы очевидно точнее, чем итерационные.
Итерационные методы позволят получить решение СЛАУ с
некоторой ошибкой;
2. точные методы требуют большое количество временных и
вычислительных ресурсов для решения СЛАУ; итерационные
методы намного быстрее и экономичнее, но за это приходится
платить погрешностью;
3. точные методы, как правило, не применяются при решении
СЛАУ, состоящих из более чем 500 уравнений из-за
длительного времени расчетов. Примечание: в реальных
задачах сетка из 500 узлов является очень маленькой.
6

7.

Тема 8. Методы решения систем линейных алгебраических
уравнений. Матричный метод.
Рассмотрим для примера уравнение, состоящее из трех неизвестных.
a11 x1 a12 x2 a13 x3 b1
a21 x1 a22 x2 a23 x3 b2
a 31 x1 a 32 x 2 a 33 x 3 b3
Важно: СЛАУ будет иметь
однозначное решение в случае,
если количество уравнений равно
количеству неизвестных.
Вопрос: что делать, если количество уравнений меньше, чем
количество неизвестных???
7

8.

Тема 8. Методы решения систем линейных алгебраических
уравнений. Матричный метод.
Рассмотрим для примера уравнение, состоящее из трех неизвестных.
a11 x1 a12 x2 a13 x3 b1
a21x1 a22 x2 a23 x3 b2
a31 x1 a32 x 2 a33 x3 b3
Запишем систему в матричном виде: AX=B.
a11 ; a12 ; a13
A a 21 ; a 22 ; a 23
a ;a ;a
31 32 33
x1
X x2
x
3
b1
B b2
b
3
Вопрос: почему матрица A представлена
именно в таком виде?
8

9.

Тема 8. Методы решения систем линейных алгебраических
уравнений. Матричный метод.
Матричное уравнение: AX=B
Правило перемножения матриц «строка на столбец»
a11 ; a12 ; a13
A a 21 ; a 22 ; a 23
a ;a ;a
31 32 33
x1
X x2
x
3
b1
B b2
b
3
Умножив матрицу A на столбец X получим:
a11x1 a12 x2 a13 x3 b1
a21x1 a22 x2 a23 x3 b2
a31 x1 a32 x 2 a33 x3 b3
9

10.

Тема 8. Методы решения систем линейных алгебраических
уравнений. Матричный метод.
Матричное уравнение: AX=B
Как найти X ?
A-1B
X=
BA-1
B/A
A-1 – обратная матрица
На матрицы делить нельзя
Умножим обе части уравнений AX=B на обратную матрицу A-1
A-1 AX= A-1 B
A-1 AX= A-1 B
X= A-1 B
Единичная матрица E. Свойство: EX=X
10

11.

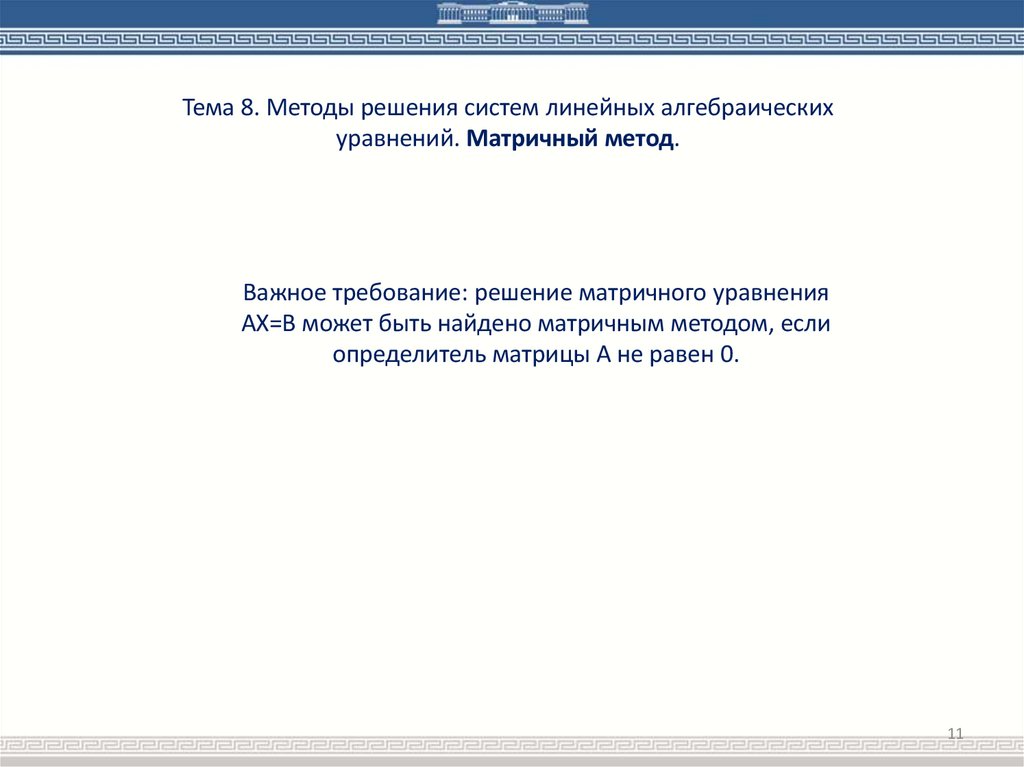
Тема 8. Методы решения систем линейных алгебраических
уравнений. Матричный метод.
Важное требование: решение матричного уравнения
AX=B может быть найдено матричным методом, если
определитель матрицы A не равен 0.
11

12.

Тема 8. Методы решения систем линейных алгебраических
уравнений. Матричный метод.
Пример: найти корни СЛАУ
x1 3 x2 5 x3 7 x4 3 x5 3
3x1 2 x2 x3 4 x4 2 x5 2
2 x1 3 x2 5 x3 6 x4 7 x5 1
4 x1 x2 2 x3 4 x4 5 x5 4
5 x1 6 x2 7 x3 8 x4 9 x5 3
Шаг 1. Записываем СЛАУ в матричном виде:
A=
1
3
2
4
5
3
2
3
1
6
5
1
5
2
7
7
4
6
4
8
3
2
7
5
9
B=
3
2
1
4
3
12

13.

Тема 8. Методы решения систем линейных алгебраических
уравнений. Матричный метод.
Шаг 2. Находим обратную матрицу A-1
В Excel это функция МОБР
A-1=
0.133333 -0.2381 -0.5619 0.390476 0.228571
-0.26667 0.428571 0.171429 -0.54286 0.161905
0.4
-0.7619 -0.6381 0.409524 0.304762
0.066667 0.333333 0.266667 -0.06667 -0.26667
-0.26667 0.142857 0.457143 -0.11429 -0.12381
Шаг 3. умножаем A-1 на столбец B: X= A-1 B
В Excel это функция МУМНОЖ
Ответ: X=
1.609524
-1.45714
1.590476
0.066667
-0.88571
13

14.

Тема 9. Метод конечных разностей для численного
решения ОДУ второго порядка.
Постановка задачи:
дано обыкновенное дифференциальное уравнение второго порядка вида
d2y
f ( x, y ),
dx 2
x [ a, b]
f ( x, y ) – некоторая функция, в общем случае, нелинейная.
Порядок ОДУ зависит от порядка производной от искомой функции.
d2y
– производная вторая, значит и порядок ОДУ – тоже второй
dx 2
Постановка задачи полная???
14

15.

Тема 9. Метод конечных разностей для численного
решения ОДУ второго порядка.
Постановка задачи:
дано обыкновенное дифференциальное уравнение второго порядка вида
d2y
f ( x, y ),
dx 2
x [ a, b]
Граничные условия: необходимо два граничных условия,
поскольку порядок ОДУ второй:
при x=a, y=C1 ; при x=b, y=C2
первое
второе
15

16.

Тема 9. Метод конечных разностей для численного
решения ОДУ второго порядка.
d2y
x
Рассмотрим простейшее ОДУ второго порядка:
dx 2
2
dy
x
Решение:
С1
dx 2
x [1,2]
(1)
x3
y
С1 x C 2 (2)
6
Общее аналитическое решение
Две константы, значит и граничных условий тоже два
ГУ: x=1, y=1 ; при x=2, y=2
Получаем систему уравнений для определения C1 и С2
13
1 С1 C 2
6
2
3
2
2С1 C2
6
Как решать будем???
16

17.

Тема 9. Метод конечных разностей для численного
решения ОДУ второго порядка.
13
1 С1 C 2
6
23
2 2С1 C2
6
Школьные методы сложения и подстановки очень трудоемки.
Матричный метод
1
2
A=
A-1=
-1
2
1
1
1
-1
x3
y
0.5 1.333
6
B= 0.833333
0.333333
X= A-1 B=
C1
1.333333 C2
-0.5
Частное решение
17

18.

Тема 9. Метод конечных разностей для численного
решения ОДУ второго порядка.
Численный метод решения
Введем обозначения:
индекс, не степень!
2
d y
f ( xi )
2
dx x x
y ( xi ) y i
i
Применим правила конечно-разностных аппроксимаций вторых
производных для левой части уравнения.
y i 1 2 y i y i 1 подставляем в ОДУ
y ' ' ( xi )
h2
y i 1 2 y i y i 1
f ( xi )
h2
Вопрос: можно ли, как в явных и неявных схемах для ОДУ первого
порядка, искать решение на следующем шаге, используя решение на
i
i 1
предыдущем шаге?
y y
hf ( xi , yi )
18

19.

Тема 9. Метод конечных разностей для численного
решения ОДУ второго порядка.
y i 1 2 y i y i 1
f ( xi )
h2
y 2 2 y1 y 0
f ( x1 )
h2
y 3 2 y 2 y1
f ( x2 )
h2
y4 2 y3 y2
f ( x3 )
h2
y5 2 y4 y3
f ( x4 )
h2
y6 2 y5 y4
f ( x5 )
h2
узел i=1
узел i=2
узел i=3
узел i=4
Что это за математическая
конструкция?
Это СЛАУ!
узел i=5
.
.
y n 1 2 y n y n 1
f ( xn )
h2
узел i=n
19

20.

Тема 9. Метод конечных разностей для численного
решения ОДУ второго порядка.
Учет граничных условий в СЛАУ
y 2 2 y1 y 0
f ( x1 )
h2
y 3 2 y 2 y1
f ( x2 )
h2
y4 2 y3 y2
f ( x3 )
h2
y5 2 y4 y3
f ( x4 )
h2
y6 2 y5 y4
f ( x5 )
h2
ГУ1
y1 C 1
y 3 2 y 2 y1
f ( x2 )
h2
y4 2 y3 y2
f ( x3 )
h2
y5 2 y4 y3
f ( x4 )
h2
y6 2 y5 y4
f ( x5 )
h2
.
.
Итоговое
СЛАУ с
учетом ГУ
.
.
y n 1 2 y n y n 1
f ( xn )
h2
ГУ2
Как будем решать СЛАУ?
yn Cn
Матричным методом
20

21.

Тема 9. Метод конечных разностей для численного
решения ОДУ второго порядка.
y1 C 1
ГУ1
y 3 2 y 2 y1 h 2 f ( x2 )
y 4 2 y 3 y 2 h 2 f ( x3 )
y 2 y y h f ( x4 )
5
4
3
2
AX=B
A=
y 6 2 y 5 y 4 h 2 f ( x5 )
.
.
ГУ2
yn Cn
21

22.

Тема 9. Метод конечных разностей для численного
решения ОДУ второго порядка.
ГУ1
A=
ГУ2
лента
Особенности матрицы A:
1) размер матрицы соответствуют количеству узлов; одна строчка – одно
уравнение для узла;
2) матрица имеет ленточный вид; вне ленты коэффициенты матрицы равны 0;
3) по диагонали стоят «-2», ее ближайшие два соседа – «1»;
4) (!!!) вне зависимости от функции в правой части вид матрицы неизменен.
22

23.

Тема 9. Метод конечных разностей для численного
решения ОДУ второго порядка.
y1 C 1
ГУ1
y 3 2 y 2 y1 h 2 f ( x2 )
y 4 2 y 3 y 2 h 2 f ( x3 )
y 2 y y h f ( x4 )
5
4
3
2
y 6 2 y 5 y 4 h 2 f ( x5 )
.
.
y C
n
AX=B
C1
2
h f ( x2 )
2
значения
h
f
(
x
)
3
функции в узлах
B h 2 f ( x4 )
сетки
2
h f ( x5 )
Информация о виде
.
C
ГУ2
функции «зашита» в
n
правой части
d2y
x cos( x)
2
dx
n
Решение: X= A-1 B
23

24.

Тема 9. Метод конечных разностей для численного
решения ОДУ второго порядка.
Пример:
Численно решить следующие ОДУ второго порядка в заданных интервалах
методом конечных разностей. Оценить относительную погрешность
численных и аналитических решений. Использовать не менее 10 узлов.
d2y
x
e
1, _ 0.5 x 1, x1 0.5, y1 2; xn 1, yn 4
2
dx
24

25.

Тема 9. Метод конечных разностей для численного
решения ОДУ второго порядка.
Шаг 1. Вычисление шага сетки. Будем использовать 10 узел. В
данном примере есть только одна координата x, поэтому сетка
будет одномерная. Вычислим шаг по формуле: h=L/(n – 1).
b a 1 0.5
h
0.055556
n 1
9
Шаг 2. Нахождение набора значений xi : xi 1 x1 ih
где i = 1, 2 … 9, x1 = a = 0.5.
25

26.

Тема 9. Метод конечных разностей для численного
решения ОДУ второго порядка.
Шаг 3. Составление матричного уравнения. Размерность
матрицы A 10·10 узлов.
A=
26

27.

Тема 9. Метод конечных разностей для численного
решения ОДУ второго порядка.
Шаг 4. Находим обратную матрицу A-1 и решаем матричное
уравнение.
A-1=
1
0.888889
0.777778
0.666667
0.555556
0.444444
0.333333
0.222222
0.111111
0
0
-0.88889
-0.77778
-0.66667
-0.55556
-0.44444
-0.33333
-0.22222
-0.11111
0
0
-0.77778
-1.55556
-1.33333
-1.11111
-0.88889
-0.66667
-0.44444
-0.22222
0
0
-0.66667
-1.33333
-2
-1.66667
-1.33333
-1
-0.66667
-0.33333
0
0
-0.55556
-1.11111
-1.66667
-2.22222
-1.77778
-1.33333
-0.88889
-0.44444
0
0
-0.44444
-0.88889
-1.33333
-1.77778
-2.22222
-1.66667
-1.11111
-0.55556
0
0
-0.33333
-0.66667
-1
-1.33333
-1.66667
-2
-1.33333
-0.66667
0
0
-0.22222
-0.44444
-0.66667
-0.88889
-1.11111
-1.33333
-1.55556
-0.77778
0
0
-0.11111
-0.22222
-0.33333
-0.44444
-0.55556
-0.66667
-0.77778
-0.88889
0
0
0.111111
0.222222
0.333333
0.444444
0.555556
0.666667
0.777778
0.888889
1
27

28.

Тема 9. Метод конечных разностей для численного
решения ОДУ второго порядка.
Шаг 5. Поиск аналитического решения
x2
y e
C1 x C 2
2
Общее решение
x2
y e
1.110879 x 0.32916
2
Частное решение
x
x
Шаг 6. Вычисление относительной погрешности численного и
аналитических решений (в процентах):
100 n y
n i 1
( численное )
( xi ) y ( аналитическое ) ( xi )
y ( аналитическое ) ( xi )
28

29.

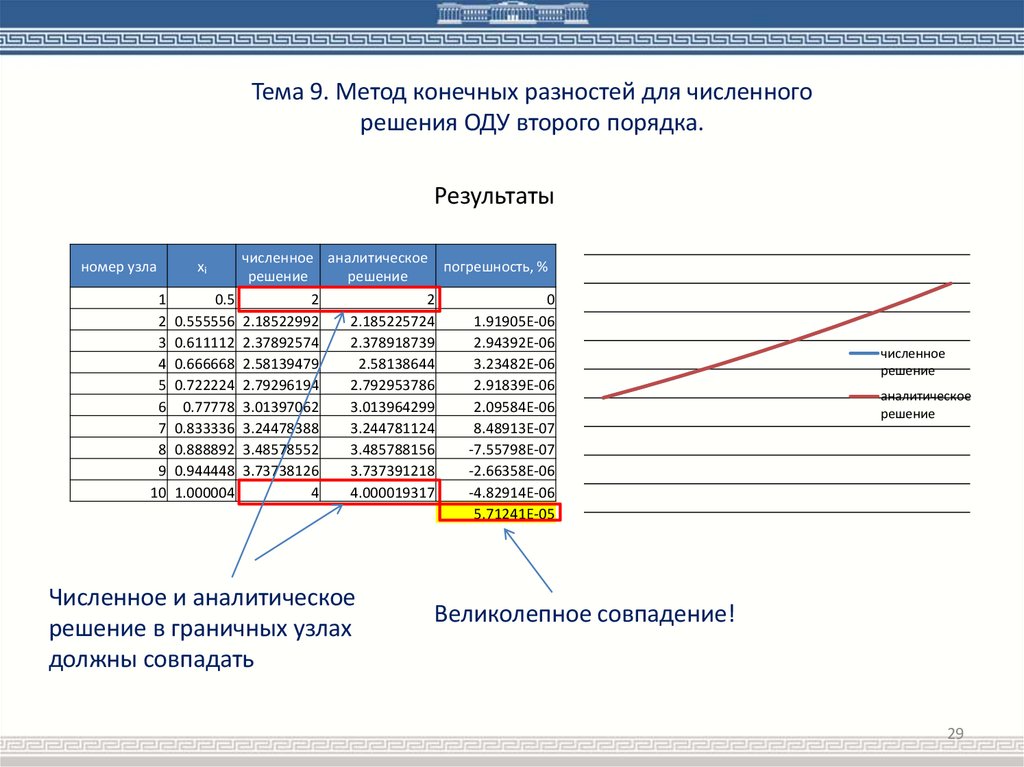
Тема 9. Метод конечных разностей для численного
решения ОДУ второго порядка.
Результаты
численное аналитическое
погрешность, %
решение
решение
1
0.5
2
2
0
2 0.555556 2.18522992
2.185225724
1.91905E-06
3 0.611112 2.37892574
2.378918739
2.94392E-06
4 0.666668 2.58139479
2.58138644
3.23482E-06
5 0.722224 2.79296194
2.792953786
2.91839E-06
6 0.77778 3.01397062
3.013964299
2.09584E-06
7 0.833336 3.24478388
3.244781124
8.48913E-07
8 0.888892 3.48578552
3.485788156
-7.55798E-07
9 0.944448 3.73738126
3.737391218
-2.66358E-06
10 1.000004
4
4.000019317
-4.82914E-06
5.71241E-05
номер узла
xi
Численное и аналитическое
решение в граничных узлах
должны совпадать
численное
решение
аналитическое
решение
Великолепное совпадение!
29

30.

Тема 9. Метод конечных разностей для численного
решения ОДУ второго порядка.
Локальная и глобальная ошибки метода
y ( xi 1 ) 2 y ( xi ) y ( xi 1 ) y ( 4 ) ( xi ) 2
y ' ' ( xi )
h
2
h
12
Остаточный член
y1 C 1
y 3 2 y 2 y1 h 2 f ( x2 ) O(h 4 )
y 4 2 y 3 y 2 h 2 f ( x3 ) O ( h 4 )
y 5 2 y 4 y 3 h 2 f ( x4 ) O(h 4 )
.
.
yn Cn
Остаточные члены,
определяющие локальную
ошибку в каждом
уравнении
Локальная погрешность имеет
четвертый порядок, значит
глобальная – третий.
30

31.

Тема 10. Основы векторного анализа.
Мотивация к изучению: большинство математических моделей
реальных природных процессов содержат векторные операторы.
divu 0
ЛР4
– уравнение неразрывности
k
u gradP – закон Дарси
ЛР5
ЛР6
1
du
u gradP – уравнение Навье-Стокса
dt
divu 0
dT
k T
dt
– уравнение неразрывности
– уравнение теплопроводности
31

32.

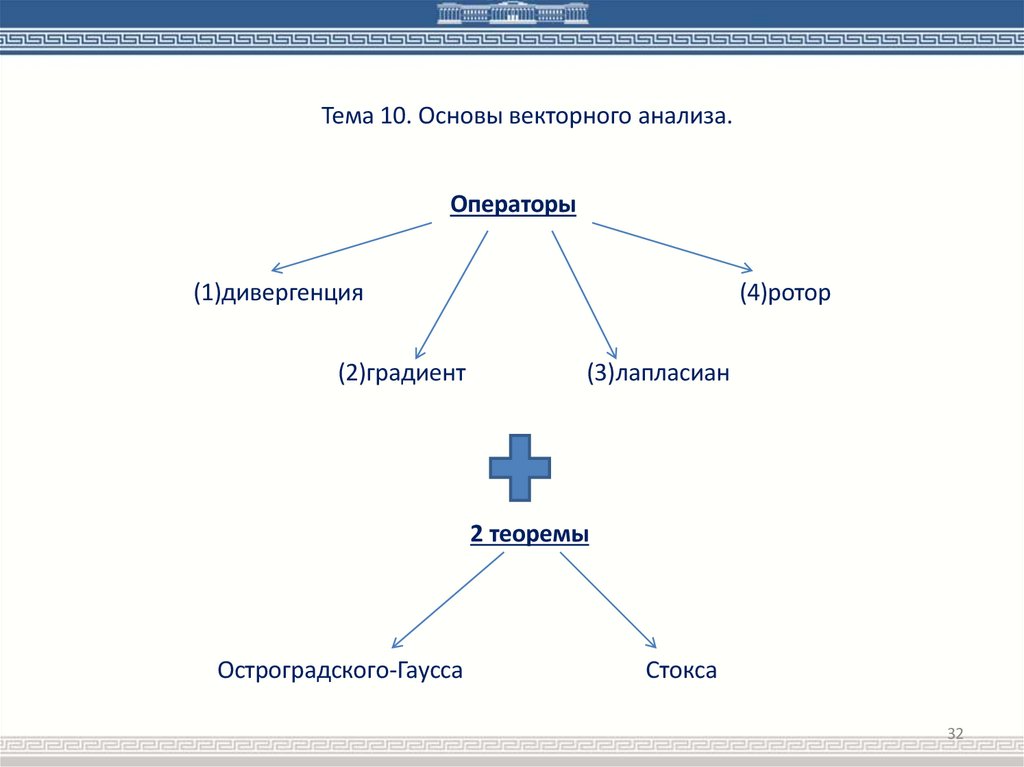
Тема 10. Основы векторного анализа.
Операторы
(1)дивергенция
(2)градиент
(4)ротор
(3)лапласиан
2 теоремы
Остроградского-Гаусса
Стокса
32

33.

Тема 10. Основы векторного анализа.
Обязательно к изучению:
Ссылка
https://www.google.ru/url?sa=t&rct=j&q=&esrc=s&source=web
&cd=&ved=2ahUKEwiymuPii5HsAhXJl4sKHcTmAIYQFjABegQIAhA
B&url=http%3A%2F%2Fold.kpfu.ru%2Ff3%2Fbin_files%2Felv!209.pdf&usg=AOvVaw0IESgLIuBFDgCCpXYnFDyx
33

34.

Тема 10. Основы векторного анализа.
(0)Оператор Гамильтона
Обозначение:
Название: «набла»
k
Пусть i, j, k – базисные вектора (орты)
декартовой системы координат.
i
_ _ _
i
j
k
x
y
z
j
34

35.

Тема 10. Основы векторного анализа.
Дивергенция
Обозначение: div
A ( Ax , Ay , Az ) Ax i Ay j Az k
вектор
_ _ _
Ax Ay Az
divA ( , A) (
i
j
k , Ax i Ay j Az k )
x
y
z
x
y
z
Скалярное произведение
число
1. Оператор Гамильтона применяется к вектору
и получается число
divC 0
2. Дивергенция от постоянной
равна
0:
3. Линейность: div( A B) divA divB
35

36.

Тема 10. Основы векторного анализа.
Градиент
Обозначение: grad
k
P P P
gradP
i
j
k
x
y
z
скаляр
i
j
36

37.

Тема 10. Основы векторного анализа.
Лапласиан
Обозначение: Δ
_ _ _ _ _ _
2 _ 2 _ 2 _
( , ) (
i
j
k,
i
j
k) 2 2 2
x
y
z
x
y
z
x
y
z
k
2P 2P 2P
P 2 2 2
x
y
z
i
скаляр
37

38.

Спасибо за внимание
38