Distant_16_09_25_Modul_svoystva_10Б

1.

16.09.25

2.

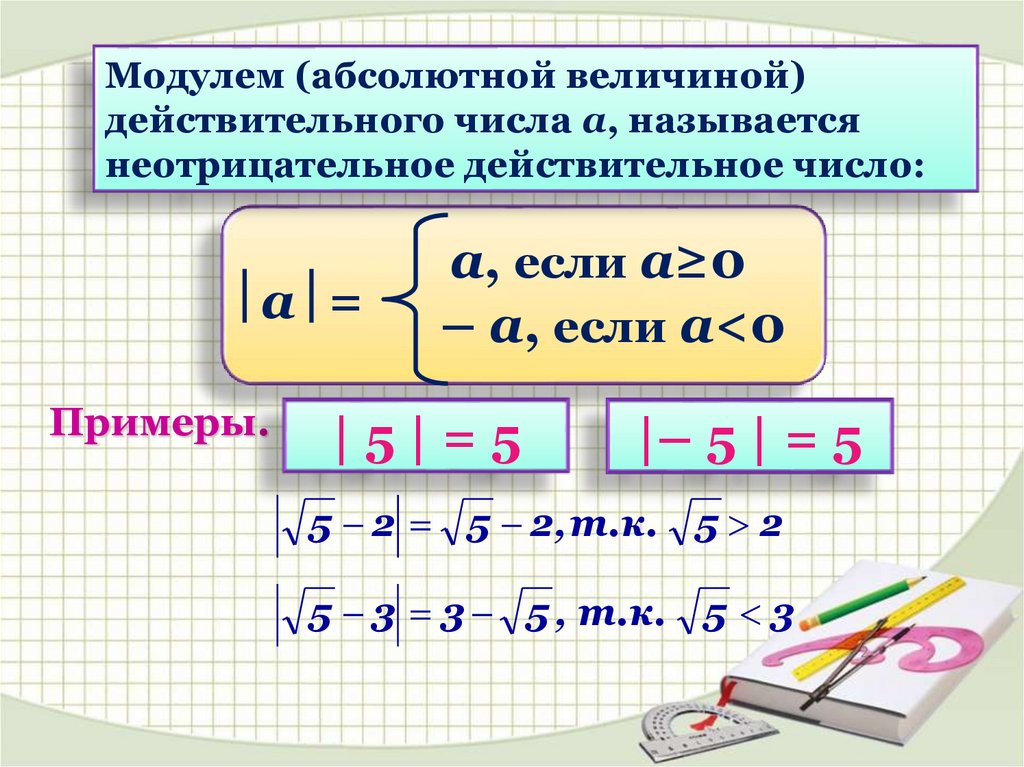
Модулем (абсолютной величиной)
действительного числа а, называется
неотрицательное действительное число:
а =
Примеры.
а, если а≥0
– а, если а<0
|5|=5
|– 5 | = 5
5 2 5 2, т.к. 5 2
5 3 3 5 , т.к. 5 3
2

3.

Заполните пропуски:
а, если ______,
а≥0
1) а
а, если а_____;
<0
____,
m
если m 0,
2) m
____,
– m если m 0.
Вычислите устно и запишите ответ:
10
1) | 5 | + | – 5 | = ___
2) | – 6 | + | 6 | = 12
__
18
3) 9 ∙ | 5 – 7 | = ___
4) | 10 – 10 | ∙ 7 = __
0
–12
5) – 3 ∙ | – 4 | = ___
6
5) | – 18 | : | – 3 | = _

4.

Основные свойства модуля
№
1
свойство
|a|≥ 0
2
|a·b|=|a|·|b|
3
a
а
b
b
4
|a|2=а2
5
|a| = | – a|
6
|a|≥ а
7
|a + b|≤ |a| + |b|

5.

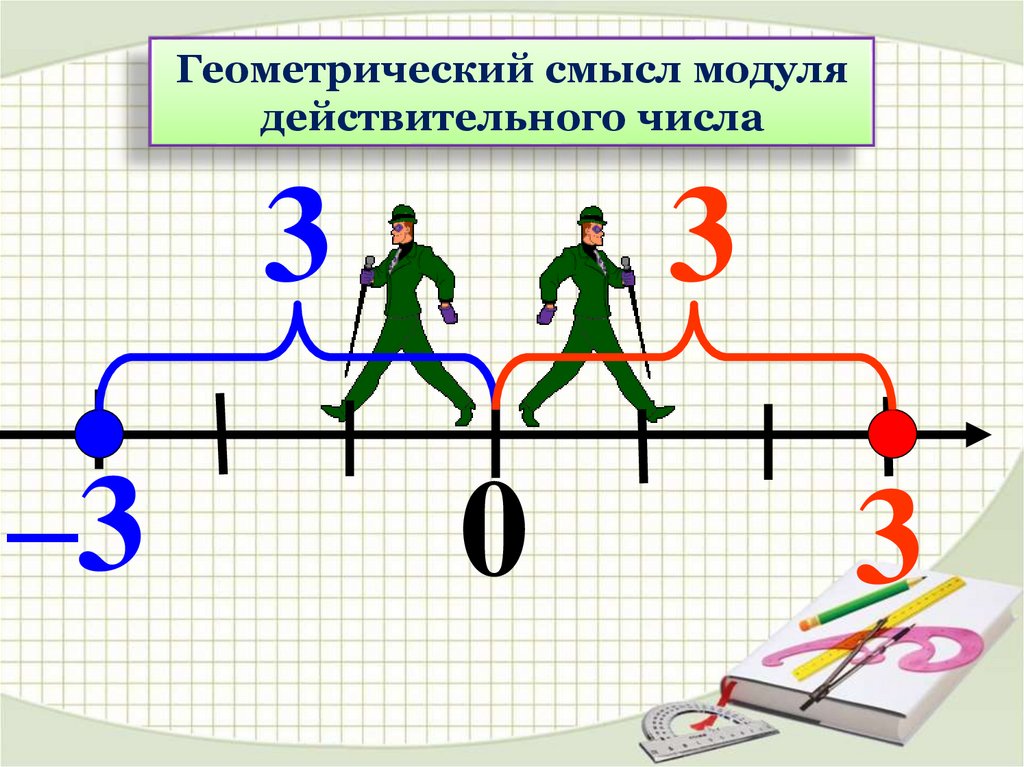
Геометрический смысл модуля
действительного числа
3
–3
3
0
3

6.

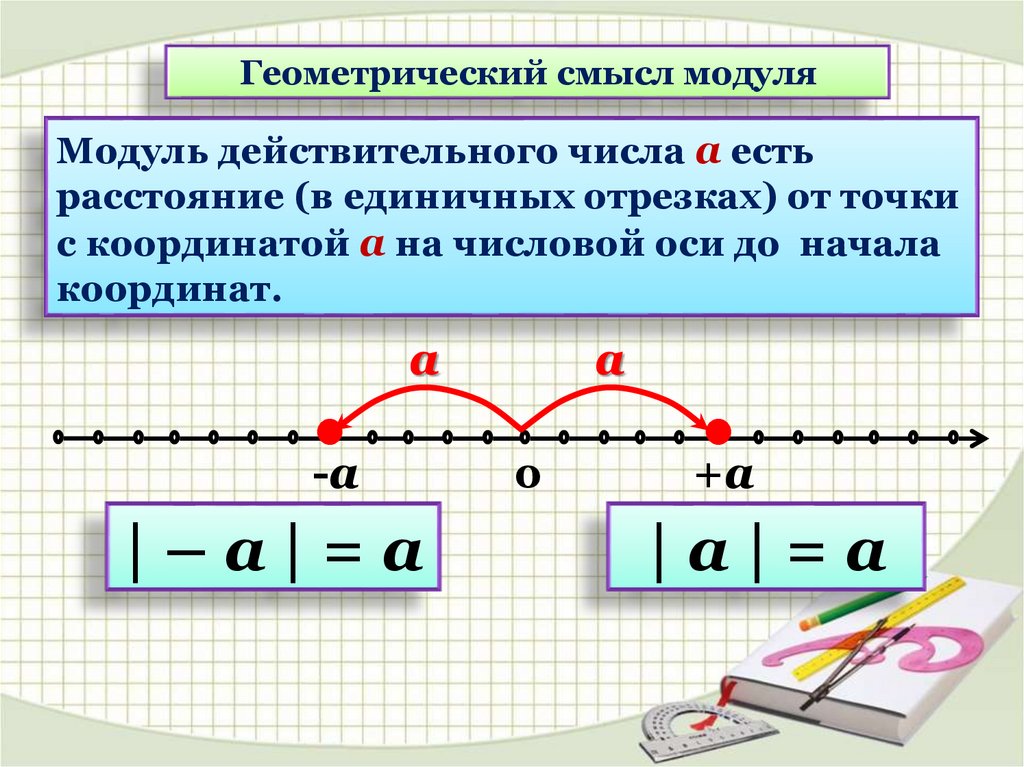
Геометрический смысл модуля
Модуль действительного числа а есть
расстояние (в единичных отрезках) от точки
с координатой а на числовой оси до начала
координат.
а
-а
|–а|=а
а
0
+а
|а|=а

7. Геометрический смысл модуля действительного числа

а
b
5
9
Расстояние между двумя
действительными числами – это
модуль разности между этими числами.
Формула расстояния между точками
a и b числовой прямой:
ρ а; b a b b a
5;9 5 9 4 4
5;9 9 5 4 4
Например:

8. Тождество

Для любого числового или
алгебраического выражения справедливо:
а а
2
Пример:
Упростить выражение
а 3
2
Возможны два случая:
а 3 а 3 а 3, еслиа 3 0
2
а 3 а 3 а 3 3 а, еслиа 3 0
2

9.

Пример №1
Упростите выражение
1)
51 7
51 5 3
2)
8 16
3)
2 5 3 5
2
2
4)
75 11
4
2
2 5 5 5
4
6
6

10.

Пример №2
1)
2)
3)
4)
Упростите выражение

11.

Пример №3
Упростите выражение
Пример №4
Упростите выражение
|х – 5| + |х – 8,5|,
если 5,6≤ х ≤8,2