Имитационное моделирование

1. ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ

Лекция 1-2
Титова Юлияна Францевна
1

2. Организация занятий

16 лекций, 16 практик, экзамен.
Балльно-рейтинговая оценка работы (файл в LMS).
Все не выполненные на практическом занятии задания надо
доделать дома (срок сдачи – следующее занятие).
В LMS материалы к лекциям и практическим занятиям,
тестовые вопросы.
Среда Anylogic 5.4.1 Anylogic 6.9.0 взять у старосты,
установить на домашнем ПК.
Консультации в период между занятиями
titova-stud@yandex.ru
2

3. Литература

1. Ю.Г. Карпов Имитационное моделирование
систем. Введение в моделирование с AnyLogic 5.
2. Е.В. Бережная, В.И. Бережной. Математические
методы моделирования экономических систем.
3. Ю.Ф. Титова материалы в LMS.
4. Аверилл М. Лоу, В. Дэвид Кельтон, Имитационное
моделирование.
3

4. Англоязычная литература по ИМЭП

5

5.

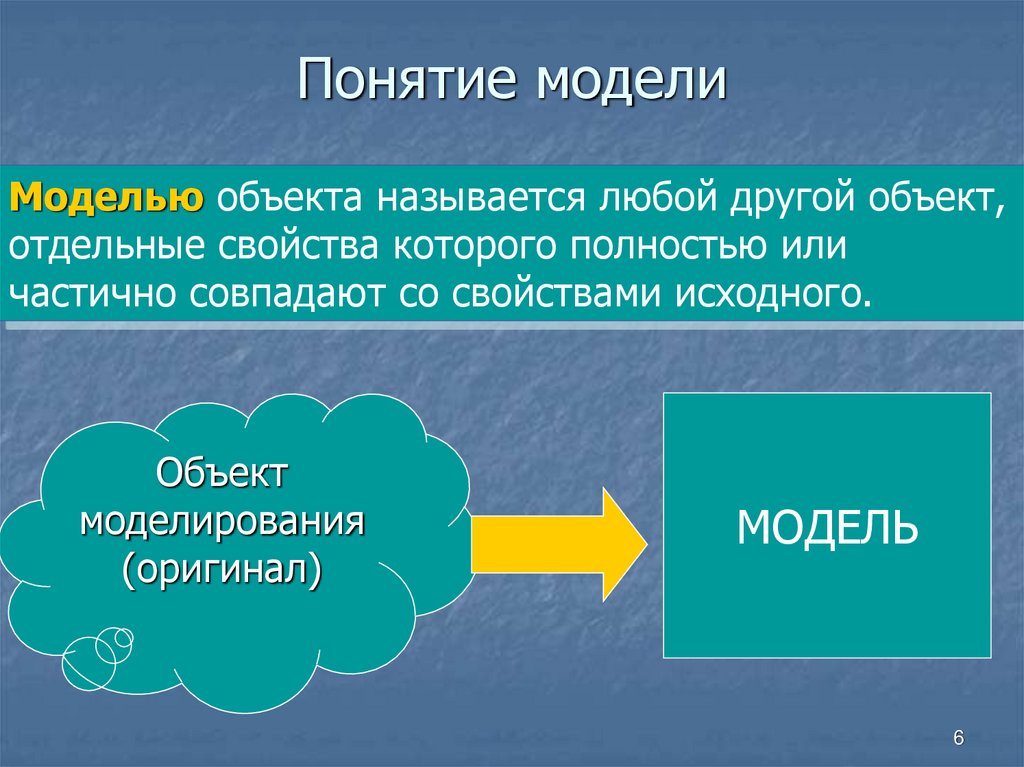
Понятие модели
Моделью объекта называется любой другой объект,
отдельные свойства которого полностью или
частично совпадают со свойствами исходного.
Объект
моделирования
(оригинал)
МОДЕЛЬ
6

6. Понятие модели

Объект моделирования
Целостный (неделимый) объект или система.
Имя, параметры и поведение.
Состояние – набор значений параметров объекта в
некоторый фиксированный момент.
Процесс – последовательная смена состояний объекта
(системы).
Поведение – законы изменения параметров объекта
(состояния) или иначе законы развития процесса.
В зависимости от целей моделирования объект
моделирования может рассматриваться как система.
Система — это совокупность объектов, например людей или
механизмов, функционирующих и взаимодействующих друг с
другом для достижения определенной цели.
Процесс в большинстве случаев представляет изменение во
времени.
7

7. Объект моделирования

Примеры процессов
H (t )
vSкр t
Sб
v – скорость вытекания частиц жидкости из крана [м/сек];
Sкр –площадь крана
Sб – площадь бассейна.
8

8. Примеры процессов

V ( x) ( a 2 x) x
2
объем коробки
а – длина стороны картонного
листа,
х – размер выреза.
9

9. Примеры процессов

Цели моделирования
средство осмысления
средство прогнозирования
нахождение оптимальных соотношений
параметров
замена исходного объекта при обучении
10

10. Цели моделирования

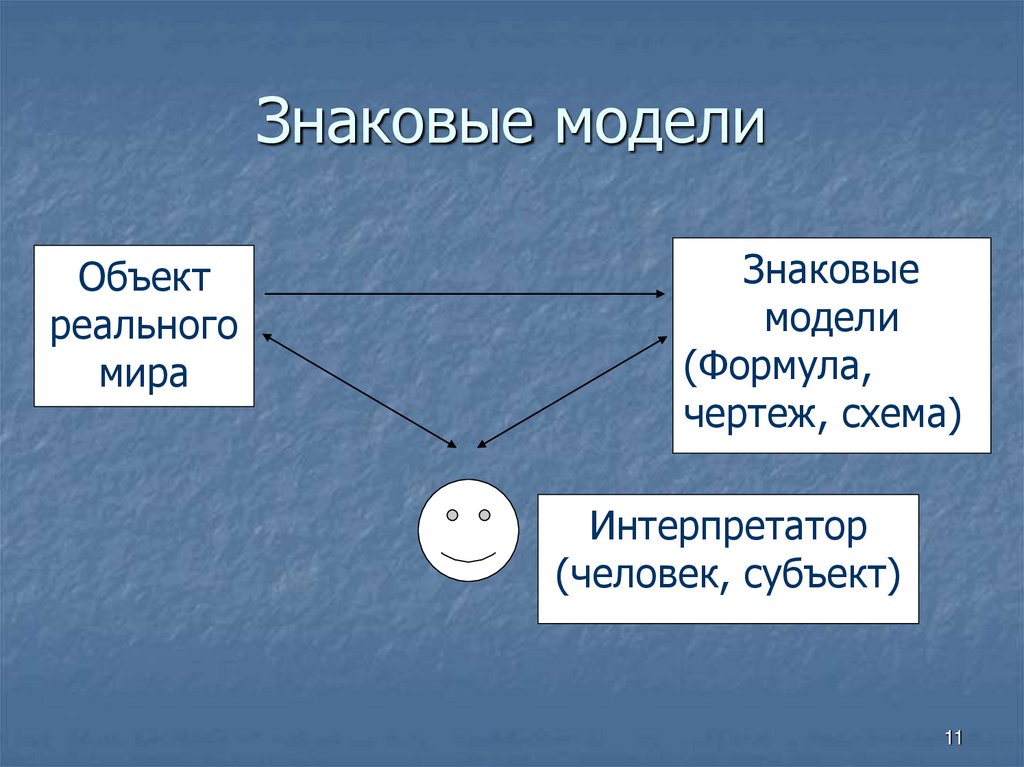
Знаковые модели
Объект
реального
мира
Знаковые
модели
(Формула,
чертеж, схема)
Интерпретатор
(человек, субъект)
11

11. Знаковые модели

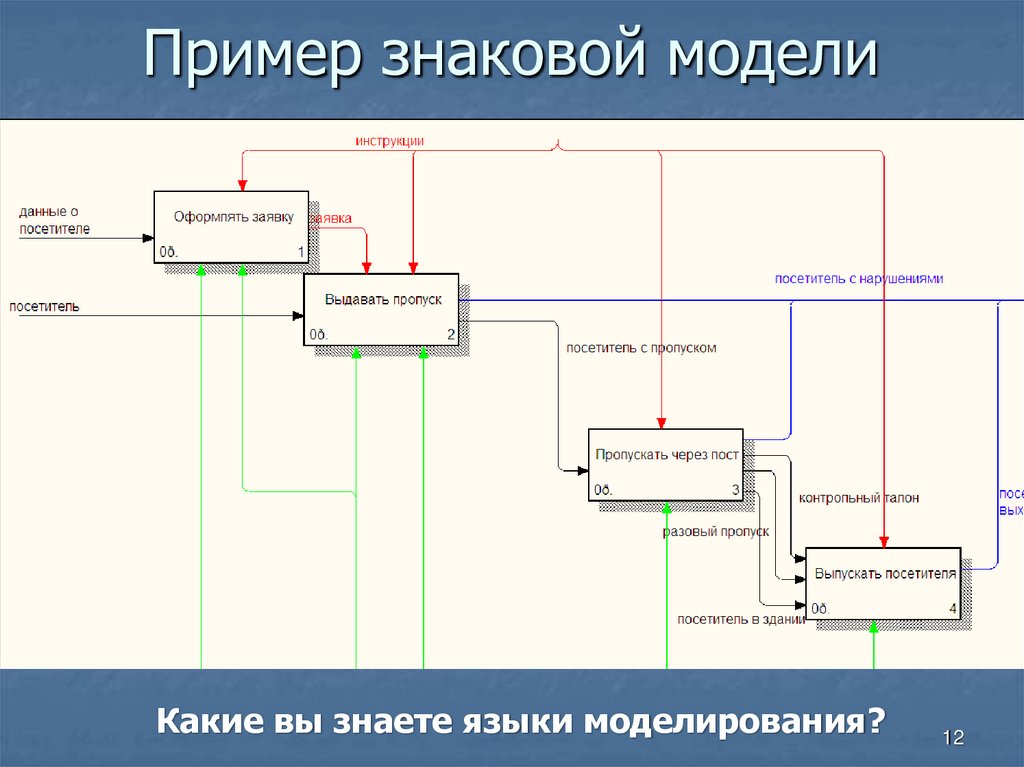
Пример знаковой модели
Какие вы знаете языки моделирования?
12

12. Пример знаковой модели

Математическая модель
Алгебраические уравнения
f ( x1 , x2 ,..., xn ) 0
Функции 1-й или нескольких переменных
y f ( x1 , x2 ,..., xn )
Матричные уравнения
AX b
Дифференциальные уравнения
f ( x, y, y , y ,..., y ) 0
(n)
13

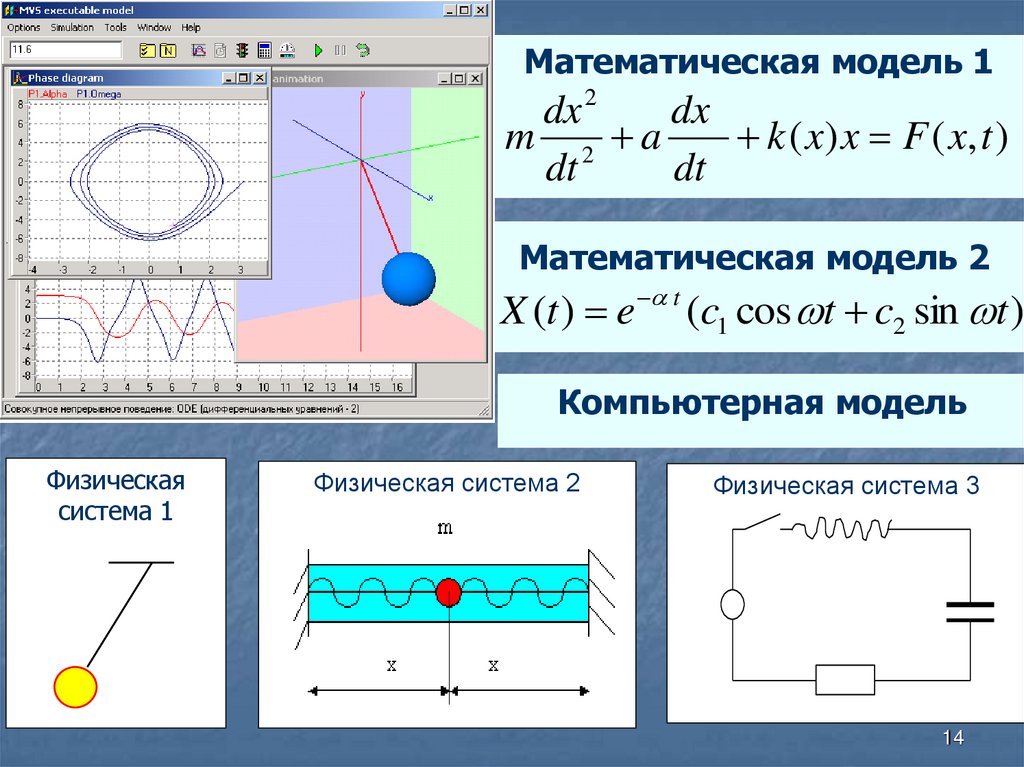
13. Математическая модель

1
dx 2
dx
m 2 a
k ( x ) x F ( x, t )
dt
dt
Математическая модель 2
X (t ) e
t
(c1 cos t c2 sin t )
Компьютерная модель
Физическая
система 1
Физическая система 2
Физическая система 3
14

14.

Динамическая система как
объект ИМ
15

15. Динамическая система как объект ИМ

Система
Система — это совокупность объектов
(элементов), например, людей или механизмов,
функционирующих и взаимодействующих друг с
другом для достижения определенной цели.
Состояние системы – совокупность параметров и
переменных , необходимых для описания системы
на определенный момент времени в соответствии с
задачами исследования.
Поведение системы – описание законов
изменения переменных.
16

16. Система

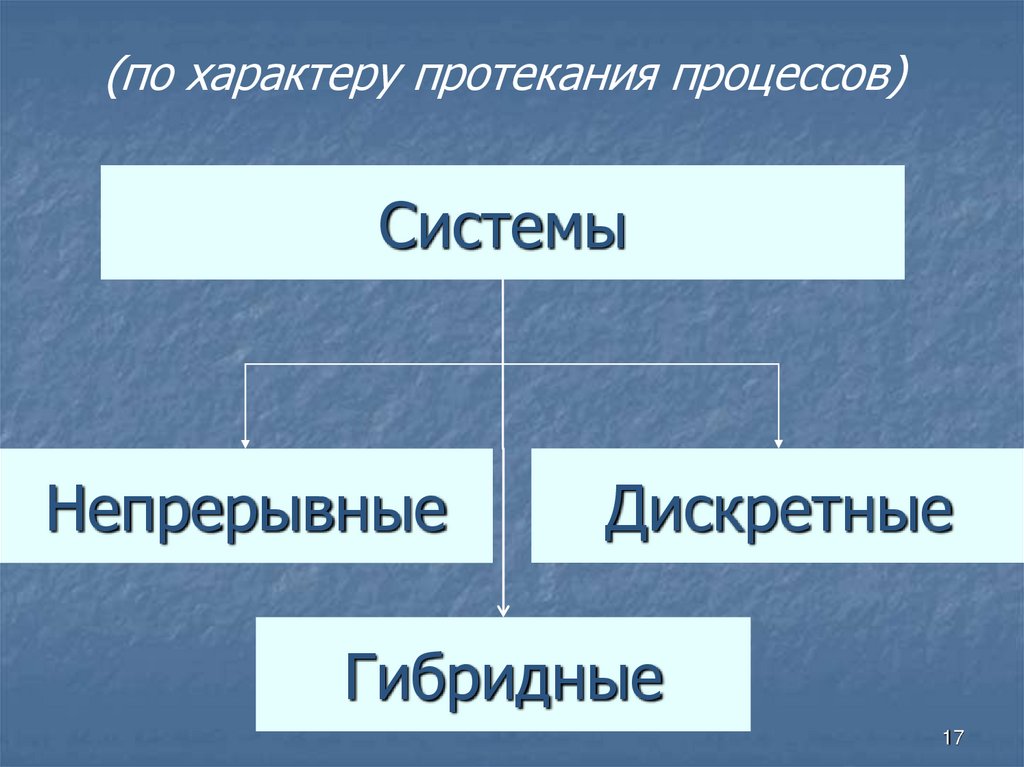
(по характеру протекания процессов)
Системы
Непрерывные
Дискретные
Гибридные
17

17. Системы

Формы описания непрерывного
поведения
1.
z z (t )
2.
G ( z (t ), t ) 0
3.
dz
F ( z, t )
dt
4.
dz
F ( , z (t ), t ) 0
dt
начальные
условия
18

18. Формы описания непрерывного поведения

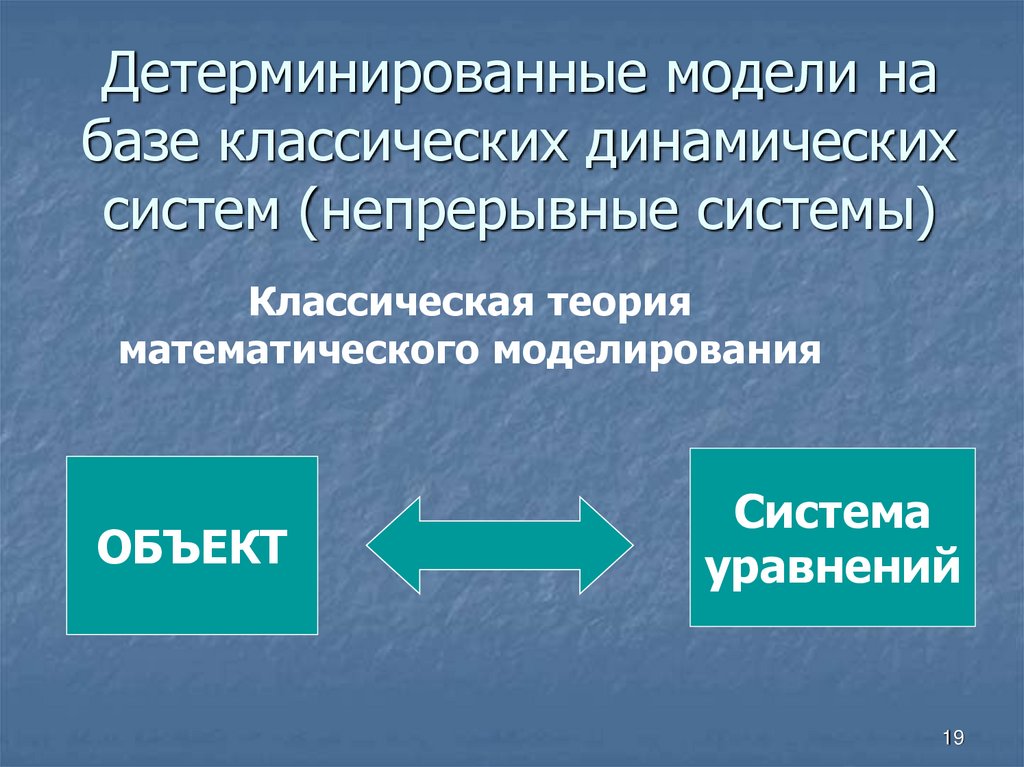
Детерминированные модели на
базе классических динамических
систем (непрерывные системы)
Классическая теория
математического моделирования
ОБЪЕКТ
Система
уравнений
19

19. Детерминированные модели на базе классических динамических систем (непрерывные системы)

ДУ как способ описания
непрерывного поведения системы
x(t ) - исследуемая переменная
dx
F ( x, t )
dt
скорость изменения переменной
20

20. ДУ как способ описания непрерывного поведения системы

Накопление средств
Модель 3. Расходы зависят от текущего капитала
А=const – фиксированная сумма, получаемая
в единицу времени
p=const – процент траты имеющихся средств
в единицу времени
Д/З
Решить ДУ
самостоятельно
dx
A px
dt
x(0) x0 ïåðâîíà÷àë üíàÿ ñóììà
ì .á. ðàâíà íóëþ
21

21. Накопление средств

Имитационная модель
Специальный программный комплекс, который
позволяет имитировать деятельность какого-либо
сложного объекта
• Отражена структура объекта (и представлена
графическим образом) со связями;
• Выполняются параллельные процессы;
• Для описания поведения могут использоваться как
глобальные законы, так и локальные, полученные
на основе натурных экспериментов
22

22. Имитационная модель

ТИПОВЫЕ ЗАДАЧИ ИМЭП
проектирование и анализ производственных систем;
определение требований к оборудованию и протоколам
сетей связи;
определение требований к оборудованию и программному
обеспечению различных компьютерных систем;
проектирование и анализ работы транспортных систем,
например аэропортов, автомагистралей, портов и
метрополитена;
оценка проектов создания различных организаций
массового обслуживания, например центров обработки
заказов, заведений быстрого питания, больниц, отделений
связи;
модернизация различных процессов в деловой сфере;
определение политики в системах управления запасами;
анализ финансовых и экономических систем.
23

23. ТИПОВЫЕ ЗАДАЧИ ИМЭП

Этапы компьютерного
моделирования
1.
ПОСТАНОВКА ЗАДАЧИ.
2.
РАЗРАБОТКА МОДЕЛИ.
3.
КОМПЬЮТЕРНЫЙ ЭКСПЕРИМЕНТ.
4.
АНАЛИЗ РЕЗУЛЬТАТОВ
МОДЕЛИРОВАНИЯ.
24

24. Этапы компьютерного моделирования

ТИПЫ ПОСТАНОВКИ ЗАДАЧИ
что будет, если…? Исследовать, как изменятся
характеристики объекта при
некотором воздействии на него.
анализ
Что будет, если изменять
чувствительности управляющее воздействие в
заданном диапазоне с некоторым
шагом.
как сделать,
Какое надо произвести воздейчтобы…?
ствие на объект, чтобы его
параметры удовлетворяли
некоторому заданному условию.
25

25. ТИПЫ ПОСТАНОВКИ ЗАДАЧИ

ПОСТАНОВКА ЗАДАЧИ
Описание задачи
2. Цель моделирования
3. Формализация задачи:
1.
- Структурный анализ системы и процессов,
протекающих в системе;
- Построение структурной и функциональной
модели системы (графическое);
- Выделение существенных для данного
исследования свойств исходного объекта
26

26. ПОСТАНОВКА ЗАДАЧИ

РАЗРАБОТКА МОДЕЛИ
Построение математической модели
Выбор программного средства
моделирования
Проектирование и отладка
компьютерной модели
27

27. РАЗРАБОТКА МОДЕЛИ

КОМПЬЮТЕРНЫЙ ЭКСПЕРИМЕНТ
Оценка адекватности построенной
компьютерной модели
Составление плана экспериментов
Исследование модели
Анализ результатов эксперимента
АНАЛИЗ РЕЗУЛЬТАТОВ
МОДЕЛИРОВАНИЯ
28

28. КОМПЬЮТЕРНЫЙ ЭКСПЕРИМЕНТ

Эксперименты для модели
«Расходы по доходам»
План экспериментов
Типы экспериментов
Теоретическое решение
29

29. Эксперименты для модели «Расходы по доходам»

Математическая модель времени
Непрерывное время – направленное течение, с
постоянной скоростью, позволяет синхронизировать
параллельные процессы
R
t
dx
dx
n
0
ff ((xx,,tt),), xx , x(0) x0
dt
d
dt
1, t (0) 0
d
30

30. Математическая модель времени

Дискретное время
упорядоченная, неограниченно возрастающая
последовательность вещественных или рациональных чисел
{t0 , t1 ,..., tk ,...}
Сеточная функция – это множество пар {t1, z(t1)}, …{ti, z(ti)}
zn dx
1 F ( zn );
f ( x, t ), x 1 , x(0) x 0
dt
Начальные
условия
z0
ti 1 ti h
z (t i h), - z (t i )
Например
f ( z (t i ), t i ), z(0) x 0
Дано z0 h
zn 1 zn 0,1 * zn ;
2
32

31. Параллельные процессы в непрерывном времени

Событийное время
любая упорядоченная последовательность явлений или
состояний объекта
{s0 , s1 ,..., sk ,....}
Гибридное время
Используется в моделях, где для описания процесса требуется
и непрерывное (дискретное) и событийное время
33

32. Дискретное время

Конец Лекции 1-2
34