Площі многокутників

1. ПЛОЩІ МНОГОКУТНИКІВ

2. Площа многокутника

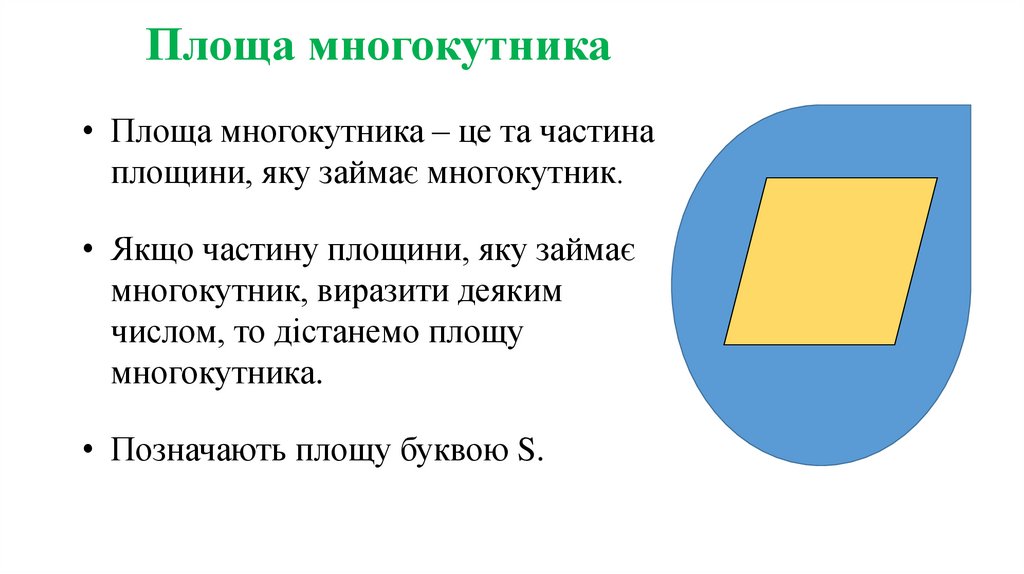
• Площа многокутника – це та частина
площини, яку займає многокутник.
ВНУТРІШНЯ
• Якщо частину
площини, яку займає
область
многокутник, виразити деяким
числом, то дістанемо площу
многокутника.
• Позначають площу буквою S.

3. Одиничний квадрат

1см 2
1 см
• Для вимірювання площі використовують
одиничний квадрат.
• Одиничним називають квадрат, довжина
сторони якого дорівнює одиниці довжини.
• Наприклад, 1 квадратний сантиметр – це
площа квадрата із стороною 1 см.

4. Площа прямокутника і квадрата

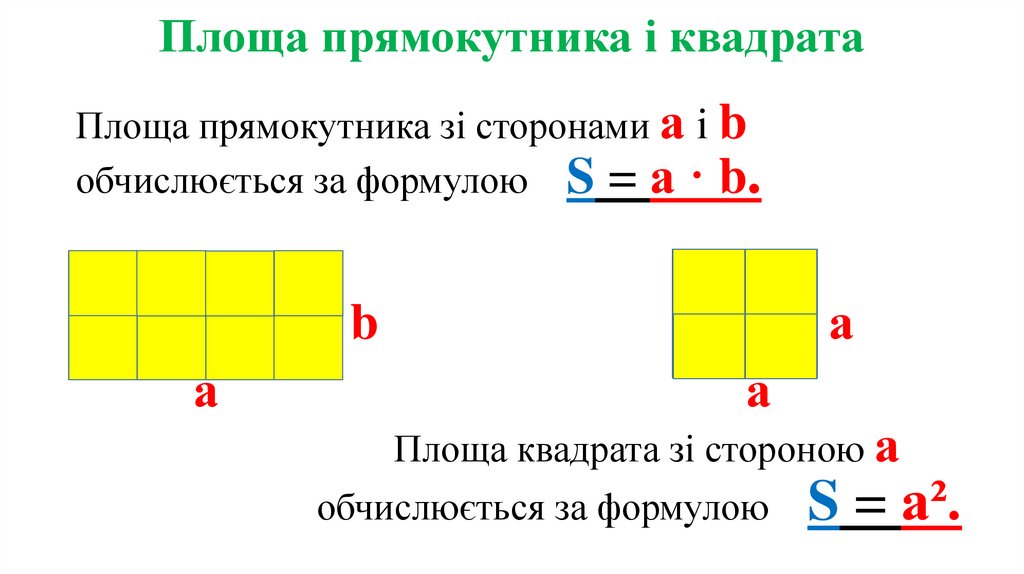
Площа прямокутника зі сторонами а і b
обчислюється за формулою S = а · b.
а
b
а
а
Площа квадрата зі стороною а
обчислюється за формулою
S = а².

5. Площа прямокутника і квадрата

Задача 1. Знайдіть сторону квадрата з площею 49 см2.
В
С
► Площа квадрата S = а²;
а = √ S ; а = √49 = 7 см.
D

6.

Задача 2. Знайдіть площу прямокутника, якщо одна з
його сторін дорівнює 12 см, а діагональ – 13 см.
В
С
13 см
12 см
D

7.

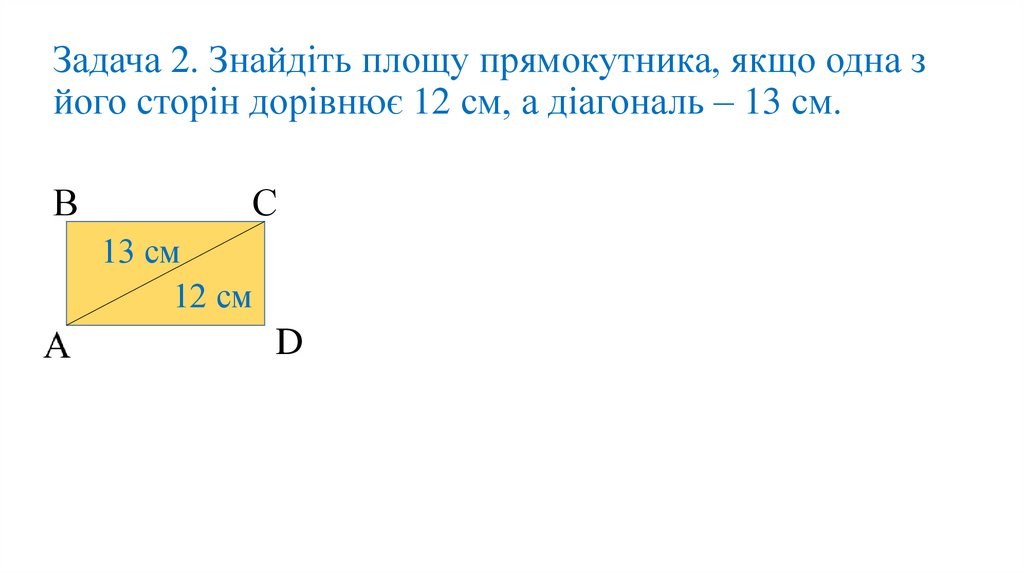
Задача 2. Знайдіть площу прямокутника, якщо одна з
його сторін дорівнює 12 см, а діагональ – 13 см.
В
С
13 см
12 см
D
► Сторона прямокутника АD = 12 см,
а діагональ АС = 13 см.
▲АСD – прямокутний. За теоремою
Піфагора АС ² = АD ² + СD².
СD² = 13² – 12² = 169 – 144 = 25; СD = 5 см.
S = АD·СD; S = 12 · 5 = 60 см².

8. Площа паралелограма

а
В
hₐ
С
С
hb
b
b
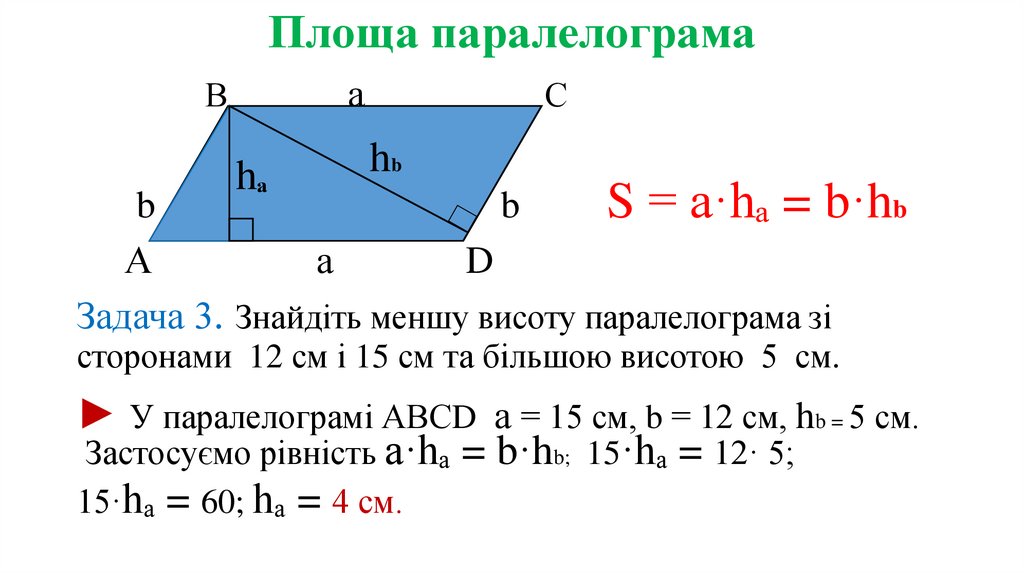
S = а·hₐ = b·hb
А
а
D
Задача 3. Знайдіть меншу висоту паралелограма зі
сторонами 12 см і 15 см та більшою висотою 5 см.
► У паралелограмі АВСD а = 15 см, b = 12 см, hb = 5 см.
Застосуємо рівність а·hₐ = b·hb; 15·hₐ = 12· 5;
15·hₐ = 60; hₐ = 4 см.

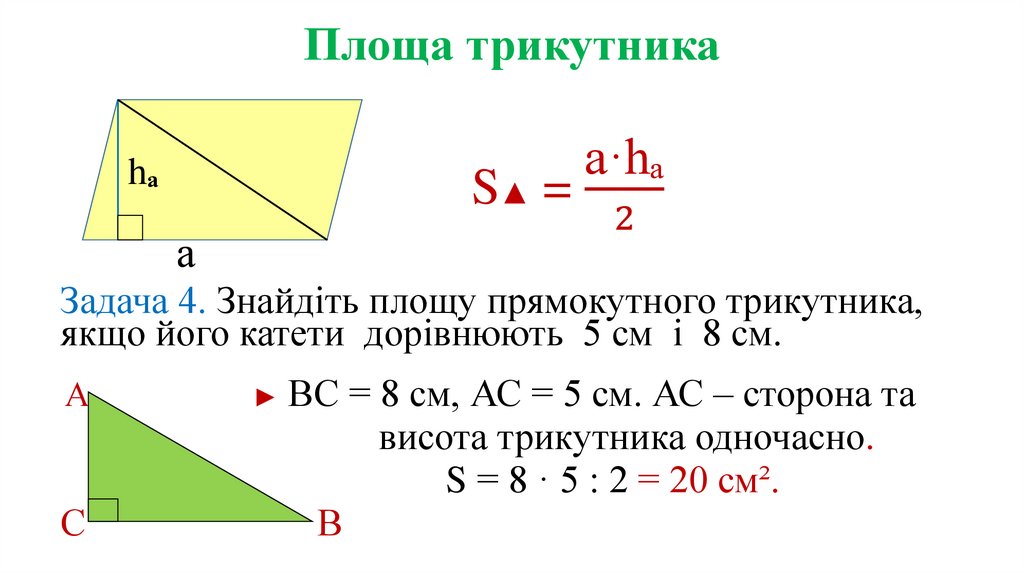
9. Площа трикутника

hₐ
S▲ =
а
а·hₐ
2
Задача 4. Знайдіть площу прямокутного трикутника,
якщо його катети дорівнюють 5 см і 8 см.
А
► ВС = 8 см, АС = 5 см. АС – сторона та
висота трикутника одночасно.
S = 8 · 5 : 2 = 20 см².
С
В

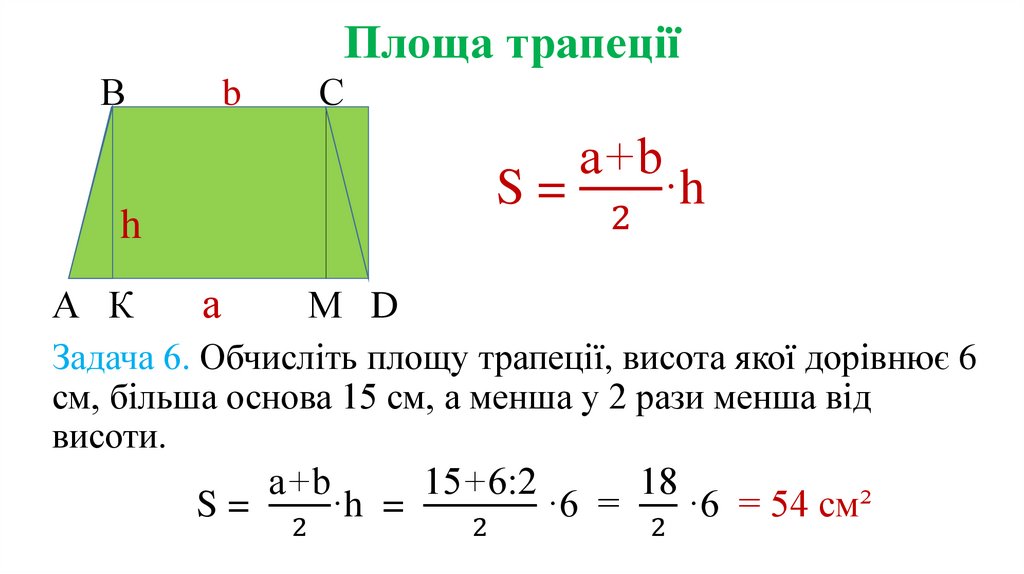
10. Площа трапеції

В
С
b
а+b
S=
·h
2
h
А К
а
М D
Задача 6. Обчисліть площу трапеції, висота якої дорівнює 6
см, більша основа 15 см, а менша у 2 рази менша від
висоти.
S=
а+b
15+6:2
2
2
·h =
·6 =
18
2
·6 = 54 см²

11.

Задача 7. Діагональ рівнобічної трапеції є бісектрисою її гострого кута
і ділить середню лінію трапеції на відрізки довжиною 5 см і 11 см.
Знайдіть площу трапеції.
► Нехай АВСD – рівнобічна трапеція з основами АD і ВС,
у якої КМ – середня лінія. Точка О – точка
перетину діагоналі АС з середньою лінією КМ.
Відрізок КО – середня лінія ▲АВС.
ВС = 2·КО = 2·5 = 10 см.
ОМ – середня лінія ▲АСD.
АD = 2·ОМ = 2·11 = 22 см.
АВС – рівнобедрений, бо < ВСА = < САD як внутрішні
різносторонні кути при прямих ВС і АD та січній АС.
▲

12.

Задача 7. (продовження)
► Отже, маємо: АВ = ВС = СD = 10 см, АD = 22 см.
ВСНТ – прямокутник. За властивістю прямокутника
ВС = ТН = 10 см.
▲АВТ = ▲DСН за катетом і гіпотенузою
АТ= НD= (АD – ТН):2 = (22 – 10):2 = 6 (см)
За теоремою Піфагора ВТ² = АВ²– АТ².
Звідки, ВТ² = 100 – 36 = 64;
Висота ВТ = 8 см. За формулою знаходимо площу трапеції.
= (22 + 10) : 2 · 8 = 128 см².

13. Домашнє завдання:

• Розвязати задачу:
Основи трапеції дорівнюють 9 см і 3 см. Знайти висоту трапеції,
якщо її площа 30 см². Зробити малюнок до задачі.