Similar presentations:
§5. Линейные ДУ1 (ЛДУ1 ). Основные понятия. Решение ЛНДУ1. Уравнение Бернулли
1.
Лекция 3.План лекции:
1. §5. ЛИНЕЙНЫЕ ДУ1
(ЛДУ1 ) .
ОСНОВНЫЕ ПОНЯТИЯ.
2. §6. РЕШЕНИЕ ЛНДУ1.
3. §7. УРАВНЕНИЕ БЕРНУЛЛИ.
1
2.
§5. ЛИНЕЙНЫЕ ДУ1(ЛДУ1 ) .
Линейным называется ДУ1 вида
y P ( x ) y Q ( x ) (5.1), где P(x) и Q(x) - функции
одного аргумента х или постоянные величины, а
у – искомая функция.
Df.1:
Zm.1: Заметим, что y и y входят в уравнение
в первых степенях и не перемножаются.
Пр.1:
1)
2
3 y 6 x x y
1
x3
ЛДУ 1 ;
3.
2) 17 ln( x 1) y y3) 5 yy x 2 y 2 3 x 0
ЛДУ 1 ;
не
является
ЛДУ 1 .
ЛДУ1 бывают двух видов:
а) Если Q(x) ≡ 0, то ЛДУ1 называется однородным ЛОДУ1 и является ДУ1 с разделяющимися переменными.
Пр.2:
1. 17 x 5y y 0;
x5
2. 2y y.
3
3
-
- ЛОДУ 1 ;
ЛОДУ1.
4.
б) Если Q(x) ≠ 0, то ЛДУ1неоднородным.
Пр.3:
называется
1. xy x 2 y sin x
- ЛНДУ1;
y
2. y 2
6 3x
x 5
- ЛНДУ1.
Для решения ЛДУ1 используются два метода:
1. метод Бернулли ( метод подстановки);
2. метод Лагранжа (метод вариации постоянной).
4
5.
§6. РЕШЕНИЕ ЛНДУ1 .Ⅰ.
МЕТОД БЕРНУЛЛИ.
Бернулли предложил представить искомую функцию у в виде произведения двух других функций ,
т.е. y = u · v (5.2), где u = u(x), v = v(x) и любая
из функций (u или v) берётся произвольно.
В результате ЛДУ1 сводится к решению двух
уравнений с разделяющимися переменными.
Рассмотрим метод на примере.
5
6.
Пр.1:2
xy y x cos x. (*)
Решение:
1). Применим подстановку (5.2), где функция v
пусть будет нулевым частным решением, а u –
новая неизвестная функция:
y = uv ⇒
y u v uv
2). Подставим в исходное уравнение (*) :
x u v uv uv x 2 cos x
xu v xuv uv x 2 cos x
xu v u( xv v ) x 2 cos x
6
(**)
7.
3) т.к. функция v - нулевое решение, то xv v 0.xv v 0
dv
x
v
dx
dx
xdv vdx xv
dv dx
v
x
dv
dx
v x
ln v ln x ,
v=x.
7
(c = 0)
8.
4) т.к. xv v 0 , то u( xv v ) 0⇒ уравнение (**) примет вид:
xu v x 2 cos x ,
где u – искомая функция ,
а v=x ⇒
x 2 u x 2 cos x
или
u cos x
u cos xdx sin x c.
5) подставим найденные значения u и v в (5.2):
y x (sin x c ) - ОР уравнения (*).
Ответ: y x (sin x c ).
8
9.
Ⅱ.МЕТОД ЛАГРАНЖА.
Метод Лагранжа по-другому называется методом
вариации произвольной постоянной.
Рассмотрим пример.
Пр.2:
xy y x 2 cos x
(*) - ЛНДУ1.
Решение:
1) Решим соответствующее однородное уравнение
xy y 0 - уравнение с разделяющимися переменными,
9
10.
xdy
y
dx
xdy ydx : xy
dy
dx
y x
ln y ln x ln c
y cx
2) Представим величину с как функцию от х, т.е.
у = с(х)·х , подставим в исходное ЛНДУ1 и найдём
значение с(х):
10
11.
x c(x) x c(x) x x 2 cos xx c (x) x c(x) c(x) x x 2 cos x
c (x) x 2 c(x) x c(x) x x 2 cos x
c (x) x 2 x 2 cos x
c (x) cos x
c(x) cos xdx
c(x) sin x c.
11
12.
3) Подставим найденное значение с(х) висходное уравнение (*):
y x sin x c
- ОР .
Ответ: y x sin x c
Zm.1:
В задачах часто встречаются линейные уравнения с постоянными коэффициентами
y ay b,
где
a; b const.
Такие уравнения решаются как все линейные уравнения или путём разделения переменных.
12
13.
§7.УРАВНЕНИЕ БЕРНУЛЛИ.
Уравнение Бернулли имеет вид
n
y P(x)y Q(x)y
(7.1),
где P(x) и Q(x) – непрерывные функции от х или
постоянные величины; n ≠ 0;1 (в противном случае
уравнение будет линейным).
Это уравнение не является линейным, но его
можно привести к линейному с помощью
подстановки
1
z n 1 .
(7.2).
y
13
14.
Пр.1:1
Решить уравнение Бернулли 3y y y 2 .
Решение:
1) 3y y y
3y y
2)
применим (7.2): z
2
1
y2
1
y
y2
3y 2 y y 3 1
z y3,
z 3y 2 y ;
отсюда получаем линейное уравнение:
14
3
y
.
2 1
15.
z z 1dz (1 z )dx
dz
1 z dx
ln 1 z x c
ln 1 z c x
1 z e
z 1 e
c x
c x
y 1 e
3
c x
y 3 1 e c x
c x
3
y
1
e
.
Ответ:
15
- ОР.
16.
Zm.1:Уравнение Бернулли также можно решать с
помощью методов подстановки и вариации
постоянной.
Решить самостоятельно:
16
1.
y y 5;
2.
3 3
y xy x y .










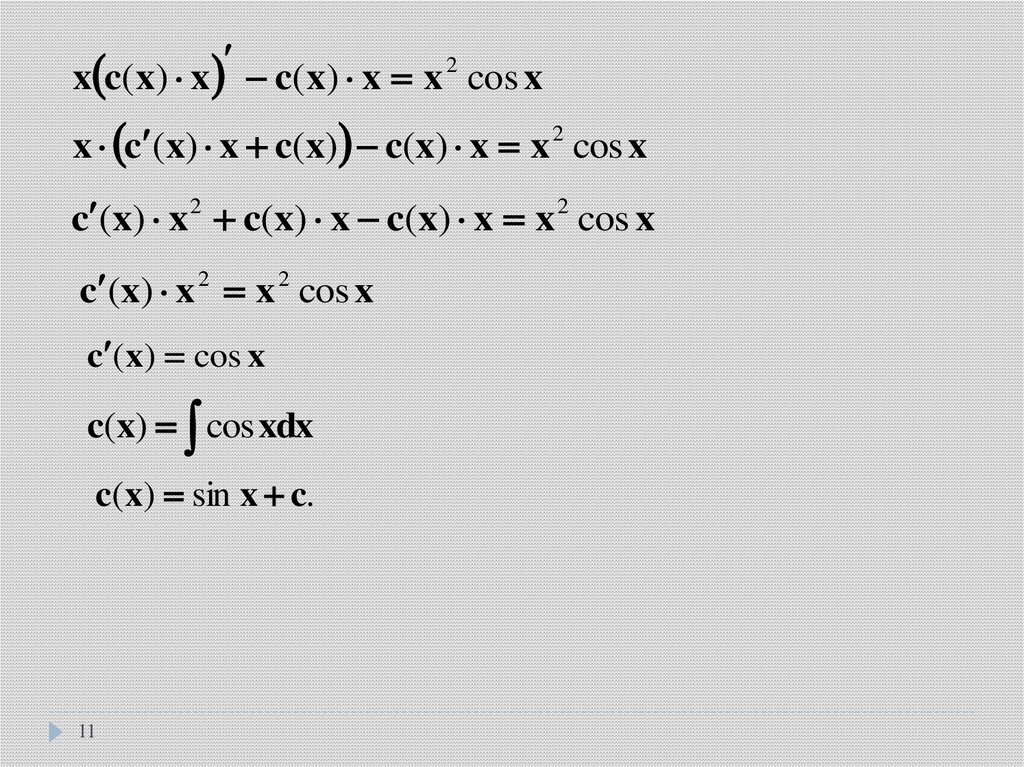





 mathematics
mathematics








