Повышение функциональной грамотности с применением методов оригами на уроках математики

1.

Повышение
функциональной
грамотности с
применением методов
оригами на уроках
математики
Шарубина Мария
КГУ «Железинская ОСШ № 1», 2025 год

2.

Актуальность темы
Жизненные задачи
Ключ к грамотности
Современный ученик должен
Математика — один из
уметь решать практические
ключевых предметов для
задачи, используя
формирования
полученные знания.
функциональной
грамотности.
Наглядность и творчество
Использование оригами позволяет сделать математику
наглядной, творческой и прикладной.

3.

Что такое функциональная грамотность?
Определение
Способность человека использовать полученные знания:
для решения практических задач;
для аргументации и принятия решений;
для понимания и интерпретации информации.
Цель:
Задачи:
Развитие функциональной грамотности через внедрение методов оригами на уроках математики.
Повысить мотивацию к изучению математики.
Развивать пространственное мышление и мелкую моторику.
Формировать навыки применения знаний на практике.

4.

Почему оригами?
Визуализация пространственных понятий
Помогает ученикам "увидеть" и понять геометрические фигуры.
Развитие логики и алгоритмического мышления
Каждое складывание — это последовательность логических шагов.
Практика пространственного воображения
Способность мысленно манипулировать объектами и формами.
Интеграция искусства и науки
Показывает связь между математикой и творчеством.
Повышение мотивации и вовлеченности
Превращает абстрактные концепции в увлекательное занятие.

5.

Примеры тем с применением оригами
"Оригами – это геометрия в действии."
— Томохиро Тачи, профессор Токийского университета
Оригами развивает навыки:
Расчёт длины, площади, симметрия
Применение оригами в математике:
Геометрия
Создание многогранников,
треугольников, симметрия.
Деление фигуры на части
Работа с пропорциями и углами
Площади и периметры
Сравнение при складывании.
Углы
Измерение углов в фигурах.
Дроби и пропорции
Деление листа, создание
симметричных частей.
Пример: складывание квадрата по диагонали — деление на
равные треугольники.
Трансформации
Отражения, повороты,
масштабирование.

6.

Пример задания: Деление квадрата на три равные части
Задача:
Возьмите квадратный лист бумаги. Ваша задача — разделить его на три абсолютно
равные части, используя только методы складывания (без измерений линейкой или
ножниц).
Опишите последовательность действий.
Как это задание помогает понять концепцию дробей (1/3) и пропорций?
Какие геометрические свойства квадрата используются в процессе?
Это задание развивает пространственное мышление, навыки точного следования
инструкциям и понимание математических принципов на практике.
Подсказка: Используйте метод "зигзаг" или метод "складывания к центральной
точке" для достижения результата.

7.

Результаты и эффекты
1
2
3
Повышение интереса к математике
Развитие межпредметных связей
Формирование практического мышления
Уроки становятся увлекательными и запоминающимися.
Соединение математики с искусством и инженерией.
Учащиеся применяют знания в реальных ситуациях.
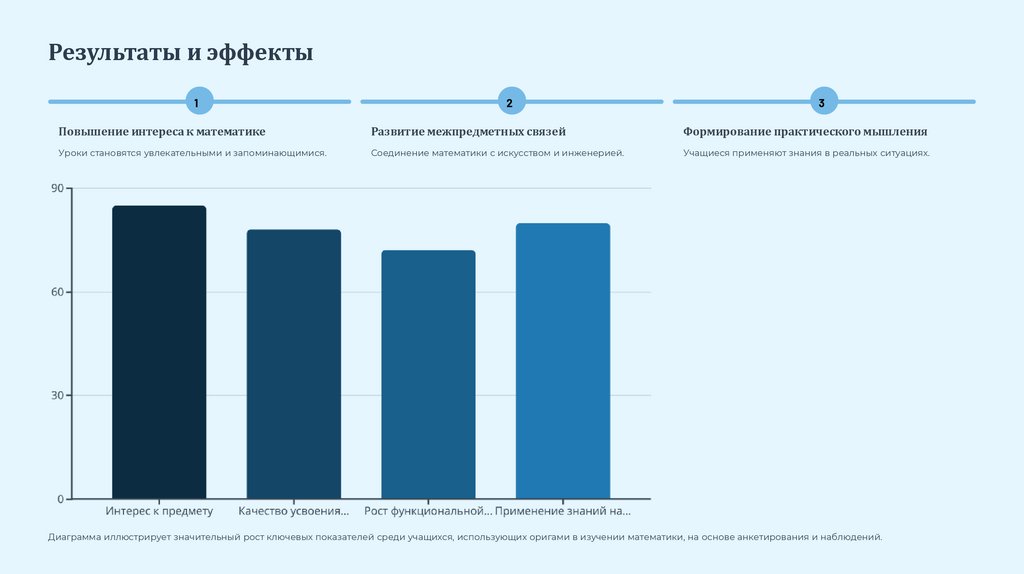
Диаграмма иллюстрирует значительный рост ключевых показателей среди учащихся, использующих оригами в изучении математики, на основе анкетирования и наблюдений.

8.

Мои работы: Геометрия в сложенных формах
Здесь представлены некоторые работы, выполненные мной и моими учениками. Каждая из них демонстрирует, как простые листы бумаги могут
превратиться в сложные математические формы, помогая осмыслить геометрию и пространственные концепции.
Эти модели — не просто поделки, а наглядные пособия для изучения симметрии, углов, пропорций и объемов.

9.

Заключение: Математика,
которую можно сложить
Оригами — это не только творчество
Но и мощный инструмент развития функциональной грамотности.
Математика становится доступной
Наглядной и невероятно интересной для каждого ученика.
Метод работает эффективно
Как на уроках, так и во внеурочной деятельности.
Путь к осознанному обучению
Оригами помогает понять, как знание применяется в жизни.
"Чтобы построить новое знание, нужно сложить его своими руками."
Альберт Эйнштейн, выдающийся физик-теоретик, лауреат Нобелевской премии
1921 года. Его слова подчеркивают важность активного, практического подхода к
обучению.

10.

Обогащаем опыт: Ресурсы и вдохновение
Пошаговые инструкции и примеры
Работы наших учеников
Отсканируйте QR-код, чтобы получить доступ к видеороликам с пошаговыми
Приглашаем ознакомиться с галереей ученических работ, демонстрирующих их
инструкциями по созданию математических оригами-моделей. От простых форм до
творческий подход и глубокое понимание математических концепций через
сложных многогранников — всё, чтобы начать применять метод прямо сейчас.
оригами. Эти примеры вдохновят вас и ваших учеников на новые открытия.