Similar presentations:
Сборник задач по теории вероятностей
1.
Б. А. СЕВАСТЬЯНОВВ. П. ЧИСТЯКОВ
А. М. ЗУБКОВ
СБОРНИК ЗАДАЧ
ПО ТЕОРИИ
ВЕРОЯТНОСТЕЙ
Д о п ущ ен о М и н и с те р с т в о м в ы сш е го
и с р е д н е г о сп е ц и а л ь н о го о б разо вани я С С С Р
в к а ч е с т в е уч е б н о го по со б и я для с т у д е н т о в .
вы сш их учебны х за в е д е н и й
М О СКВА
аН А УКА»
ГЛ А В Н А Я Р ЕД А К Ц И Я
Ф И З И К О -М А Т Е М А Т И Ч Е С К О Й Л И Т ЕР А Т У Р Ы
1980
2.
22.171С 28
У Д К 519.2
С е в а с т ь я н о в Б. А. , Ч и с т я к о в В . П. ,
З у б к о в А. М. Сборник задач по теории
вероятностей.— М .: Наука, Главная редакция
физико-математической литературы, 1980.
Входящие в сборник задачи обеспечивают
упражнения по всем разделам теории вероят
ностей, включаемым в начальный курс. Текст
задач, указания и ответы помещаются раздельно.
Перед каждой темой дается перечень основных
теоретических положений. Приводятся необхо
димые для решения задач таблицы.
©
С
20203-109
053 (02)-80
19-80. 1702060000
И зд а тел ьство «Н аука*
Главная редакция
ф изико-математической
л итературы , 1980
3.
ОГЛАВЛЕНИЕП р е д и с л о в и е ...............................
. . .
5
Ч А С Т Ь I. ЗАДАЧИ .................................................................................
Глава
1. Простейшие вероятностные схемы
7
§ 1. Классическое определение в ер оя тн ости .................
§ 2. Геометрические в ер оя тн ости ...........................................
Глава
10
17
..........................
21
§ 1. Условные вероятности
...................................................
§ 2. Независимость с о б ы т и й ...................................
29
31
§ 3. Формула полной в е р о я т н о с т и .......................
§ 4. Схема Б е р н у л л и
. . .
§ 5. Полиномиальная с х е м а ...................................................
27
Глава
2. Последовательности испытаний .
7
38
3. Случайные в е л и ч и н ы ...................................................
§ 1. Распределения вероятностей случайных величин
§ 2. Математические
ож и д а н и я ....................................
§ 3. Условные р а сп р е д е л е н и я ...............................
71
§ 4. Нормальное р а сп р е д е л е н и е ..........................
75
Глава
34
40
50
58
4. Предельные теоремы. Производящие и характе
ристические ф у н к ц и и ........................................
§ 1. Закон больших
чисел. Лемма
Бореля — Кантелли85
§ 2. Прямые методы
доказательства предельных теорем 89
§ 3. Характеристические и производящие
функции
98
§ 4. Неравенства Бонферрони и сходимость к распре
делению П у а с с о н а ..........................................
107
§ 5. Применения центральной предельной теоремы
и метода характеристических функций . . . . .
НО
Глава
5. Цепи Маркова
Глава
6. Элементы математической статистики
ЧА С ТЬ
..........................................................
. . . .
116
125
И. У К А З А Н И Я ........................................................................
135
3
4.
ЧАСТЬШ . РЕШЕНИЯ
• « . • • • • • • • • • • • • •
180
ЧАСТЬ
IV. ОТВЕТЫ
............................. .
198
Таблицы:
. . . . .
215
Нормальное р а сп р е д е л е н и е ......................................... . ,
Распределение П у а с с о н а
. . . . . . . .
Распределение Стьюдента
. . . . . . ........................
^-распределение
..................................
Равномерно распределенные случайные числа . . . .
Нормально распределенные случайные числа . . . .
215
217
218
219
220
221
Литература
. . . . . . . . . . . .
..........................................
...........................................................................
223
5.
ПРЕДИСЛОВИЕЭтот сборник задач предназначен для студентов университетов
и технических вузов в качестве учебного пособия по начальному
курсу теории вероятностей. Для решения большей части задач не
требуется знаний, выходящих за пределы обычного курса по ма
тематике для технических вузов. Лишь задачи 1.19— 1.22, 2.18— 2.20,
3.114—3.132,
3.147— 3.160,
4.9— 4.22, 4.41— 4.55, 4.89— 4.94,
4.101— 4.115, 4.135— 4.140 рассчитаны главным образом на сту
дентов университетов.
Свободное владение понятиями и методами теории вероятно
стей необходимо не только математикам, но и прикладникам,
потому что при решении практических задач огромную роль
играет правильность выбора вероятностной модели: она должна,
во-первых, отражать существенные черты исследуемого явления,
а во-вторых, быть доступной для исследования. Подобрать модель
и оценить это ее последнее качество, не имея представления о тео
рии вероятностей и ее методах, невозможно.
В нашем сборнике сравнительно мало задач, сформулирован
ных в «прикладных» терминах. Это объясняется несколькими при
чинами: общностью курса теории вероятностей й разнообразием
узких специализаций технических вузов, ограниченностью объема
книги и желанием авторов дать учащимся больше сведений о мето
дах теории вероятностей. Как уже отмечалось, решение «приклад
ных» задач состоит из двух этапов: формулировки «прикладной»
задачи как математической и решения этой математической задачи.
Авторы считают, что прежде всего нужно ознакомить студентов
со стандартными моделями теории вероятностей и научить их
преодолевать трудности второго этапа; именно с таким расчетом
и проводился отбор задач. Обучение способам построения матема
тических моделей реальных явлений не следует подменять реше
нием задач, отличающихся от простых математических задач только
«прикладной» терминологией; здесь, видимо, нужно использовать
те модели реальных явлений, которые на самом деле используются
в областях науки и техники, близких к специализации того или
иного технического вуза. Ряд задач последнего типа можно найти
в сборнике задач [3] под общей редакцией А. А. Свешникова.
4
6.
В нашем сборнике задачи, решение которых сводится к подстановке чисел в формулы, составляют меньшую часть. Авторы
стремились подобрать задачи так, чтобы помочь учащемуся не
только освоиться с основными понятиями и методами теории вероят
ностей, но и почувствовать взаимосвязь между понятиями, а также
оценить возможности методов.
В связи с этим ряд задач имеет «теоретический» характер:
в них требуется доказать справедливость того или иного утверж
дения или провести небольшое исследование. Как правило, такие
задачи образуют довольно четко выделенные циклы, и при последо
вательном решении эти задачи не должны представлять больших
трудностей. Трудность задач значительно понижается, если пользо
ваться указаниями (часть II). Для задач, номера которых отме
чены звездочкой, приведены решения.
Теоретические задачи часто содержат материал, которому уде
ляется мало внимания в стандартных курсах теории вероятностей,
но который является важным в принципиальном отношении. Осо
бенно это относится к таким «техническим» приемам решения
задач, как представление искомой случайной величины в виде
суммы индикаторов, использование линейности математического
ожидания, введение производящих и характеристических функций,
метод моментов, рассмотрение случайных величин, мало отличаю
щихся от заданных, но проще исследуемых, и т. п.
При составлении задачника был использован ряд отечествен
ных и зарубежных источников (учебников, задачников, журналь
ных статей и т. п.), а также задачи, известные в научных и педа
гогических коллективах, хорошо знакомых авторам (МИАН,
мех.-мат. МГУ, МФТИ, МИФИ и др.)*
Авторы
7.
Ч асть8,
ЗАД АЧ И
Глава 1
ПРОСТЕЙШИЕ ВЕРОЯТНОСТНЫЕ СХЕМЫ
Математические модели случайных явлений, рас
сматриваемые в теории вероятностей, основываются на
понятии вероятностного пространства, т. е. тройки
(£2, Л, Р), где £2 = {со} — непустое множество, элемен
ты со которого интерпретируются как взаимно исклю
чающие исходы изучаемого случайного явления; Л — на
бор подмножеств множества £2, называемых событиями
(предполагается, что множество Л содержит £2 и замк
нуто относительно взятия противоположного события
и суммы событий в не более чем счетном числе, т. е. Л
является cr-алгеброй); вероятность Р — функция, опре
деленная на событиях А £ Л и удовлетворяющая сле
дующим условиям:
1. Р ( А ) ^ 0 при любом А £ Л .
2. Р (£2)= 1.
бых 1 Ф } . Здесь символ 0 обозначает пустое множе
ство (или невозможное событие).
Определение операций над событиями, определение
алгебры и о-алгебры событий можно найти в учебни
ках по теории вероятностей (см., например, [4], [2],
[12]). В этой главе рассматриваются два простейших
класса вероятностных пространств.
Пусть Q = {сох, со2, . . . , со5}. В о-алгебру событий Л
включаются все 2s подмножеств А = {со1-1, . . . , сotft} мно
жества £2. В классическом определении вероятности
полагают все P(co/) = l/s, поэтому вероятность Р( А)
события A = {o)ilf
сoib\ равна отношению числа эле
7
8.
ментарных событий *) <ot, входящих в Л, к общемучислу элементарных событий в Я:
р<
л>=-тМ-
<12>
Классическое определение вероятности является хо
рошей математической моделью тех случайных явле
ний, для которых исходы опыта в каком-либо смысле
симметричны, и поэтому представляется естественным
предположение об их равновозможности.
Дадим описание двух часто встречающихся вероятно
стных схем, в которых детализируется общее класси
ческое определение. Обозначим через dV* множество
из N чисел: оЛГ= {1, 2, . . . ,
пусть со = (i19 t2, . . . , in) —
упорядоченный набор из п элементов множества off.
Вероятностную схему, в которой
Q = {со = (i19 i2, . . . , in) : ik £ qAT, &= 1, 2, .. ., n)
(1.3)
и все элементарные события со равновероятны, назы
вают схемой случайного выбора с возвращением.
Схемой случайного выбора без возвращения называют
вероятностную схему, в которой
£2
{со == (tj, i2f . . . , in) :
среди il9
£
oj\P, k = 1, 2, . . . , n,
in нет одинаковых}
(1.4)
и элементарные события со равновероятны.
При вычислении вероятности по формуле (1.2) часто
оказываются полезными различные комбинаторные фор
мулы. Приведем основные из них. Пусть дано мно
жество оДГ из N элементов: oJ\P= {ai, а2, . . . , aN\. Под
множества множества оДГ называют сочетаниями. Число
сочетаний, которые можно образовать из N элемен
тов оДГ, выбирая различными способами подмножества
по п элементов, обозначают С% или ^ ^ .С п р а в е д л и
вы формулы:
пп
р п
п\
*
N\
р п __
— n \ (N — n)\ ’
где п\ = 1 •2 • . . . •п и
N W = N ( N — 1) . . . ( N - n + 1).
*
(1.5)
*) Здесь и ниже число элементов любого конечного множе
ства М будем обозначать |М |.
8
9.
Упорядоченные цепочки altaia . . . ain, образованные изразличных элементов <ЛР, называют размещениями.
Число размещений, образованных выбором различных
упорядоченных цепочек длины п из N элементов el\P,
обозначают А%. Для А% имеем формулу A% = N W .
Частный случай размещений при n — N называют пере
становками,. Число различных перестановок, образо
ванных из N элементов, равно N1
Часто оказывается полезной следующая класси
ческая формула, известная как уточненная формула
Стирлинга (см. [11], стр. 67, (9.8)):
п \ = У 2 к п п ”е ~ « ё ™ ,
(1-6)
В формулировках некоторых задач используется
выражение: «целое число а сравнимо с целым числом b
по модулю т» (т — целое), или в символической записи
а =ее b (mod т).
(1.7)
Сравнение (1.7) эквивалентно утверждению: существует
такое целое число t, что а — b = tm (т. е. а и b при
делении на т дают одинаковые остатки). В частности,
запись а = 0 (mod т) означает, что а делится без
остатка на т.
Целую часть действительного числа х (наименьшее
целое число, не превосходящее х) будем обозначать [х]
(не путать с аМ , где х — целое число, см. (1.5)).
Рассмотрим второй класс общих вероятностных про
странств. Пусть Q — ограниченное множество п-мерного
евклидова пространства. Будем предполагать, что Q
имеет объем. Рассмотрим систему Л подмножеств £2,
имеющих объем. Для любого А £ Л положим
р ( Л) “ д а | ’
<>-»)
где р (С )— объем множества С. Если под объемом мно
жества понимать его меру Лебега, то система Л — это
ст-алгебра измеримых по Лебегу множеств, и тогда функ
ция Р(Л), определенная формулой (1.8), является
вероятностью. Отметим, что система Л , в частности,
содержит все подмножества Q, измеримые по Ж ордану,
т. е. обычные квадрируемые или кубируемые фигуры,
которые изучаются в любом курсе математического
анализа. В большинстве задач рассматривается именно
9
10.
этот частный случай. Определение вероятности (1.8)называют геометрическим определением вероятности.
Приведем формулы, которые часто используются
при решении задач. Для любых событий А 19 Л2, . . .
имеем
и 4 =
п= 1
п i
П лп=
п= 1
/1=1
U А а.
п —1
(1.9)
При любых А и В верна формула
Р (А + В) = Р (Л) + Р (В) — Р (ЛЯ),
в частности, при А В = 0
(1.10)
имеем
Р(Л + В) = Р( Д) + Р (В).
(1.11)
Вероятность суммы произвольных п событий находится
по формуле
Р(Лх + Л 2+ • • • + ^ п ) == 2
k=\
+
k) —
i
2
P
S
Р {AktAk2) ~f*
—
_ . . . + ( - 1 ) » - » Р ( Л 1Л1 . . . Л„) =
-= S (— 1)г- х
J= 1
2
< k [ <^n
Р ( Л , , . . . (1.12)
Во всех задачах § 1 данной главы предполагается,
что элементарные события равновероятны; слова «слу
чайно», «случайно выбирается» нужно понимать как
предположение о равновероятности элементарных со
бытий. В § 2 выражение «точка равномерно распреде
лена на множестве Q» означает, что вероятности нужно
вычислять по формуле (1.8).
§ 1. Классическое определение вероятности
1.1.
Из ящика, содержащего три билета с номера
ми 1, 2, 3, вынимают по одному все билеты. Предпо
лагается, что все последовательности номеров билетов
имеют одинаковые вероятности. Найти вероятность
того, что хотя бы у одного билета порядковый номер
совпадает с собственным.
to
11.
1.2. Колода из 36 карт хорошо перемешана (т. е.все возможные расположения карт равновероятны).
Найти вероятности событий:
А = {четыре туза расположены рядом},
В = {места расположения тузов образуют
арифметическую прогрессию с шагом 7}.
1.3. На полке в случайном порядке расставлено
40 книг, среди которых находится трехтомник А. С. П уш
кина. Найти вероятность того, что эти тома стоят в по
рядке возрастания слева направо (но не обязательно
рядом).
1.4. Брошено три монеты. Предполагая, что эле
ментарные события равновероятны, найти вероятности
событий:
А = {первая монета выпала «гербом» вверх},
В = {выпало ровно два «герба»},
0 = {выпало не больше двух «гербов»}.
1.5. Из множества всех последовательностей длины п,
состоящих из цифр 0, 1, 2, случайно выбирается одна.
Найти вероятности событий:
А = {последовательность начинается с 0},
В = {последовательность содержит ровно т + 2 нуля,
причем 2 из них находятся на концах последователь
ности},
С = {последовательность содержит ровно т единиц},
D = { в последовательности ровно т 0 нулей, т1 еди
ниц, т2 двоек}.
1.6. Из 28 костей домино случайно выбираются две.
Найти вероятность Р 2 того, ч ю из них можно соста
вить «цепочку» согласно правилам игры.
1.7. В записанном телефонном номере 135— 3 .— ..
три последние цифры стерлись. В предположении, что
все комбинации трех стершихся цифр равновероятны,
найти вероятности событий:
А = {стерлись различные цифры, отличные от 1, 3, 5},
В—
—{стерлись одинаковые цифры},
С = {две из стершихся цифр совпадают}.
1.8. Какова вероятность того, что четырехзначный
номер случайно взятого автомобиля в большом городе:
а) имеет все цифры разные? б) имеет только две одии
12.
наковые цифры? в) имеет две пары одинаковых цифр?г) имеет только три одинаковые цифры? д) имеет все
цифры одинаковые?
1.9. Найти вероятность pN того, что случайно взя
тое натуральное число из множества {1, 2,
N\
делится на фиксированное натуральное число k. Найти
lim pN.
N
- * оо
1.10. Из чисел {1, 2,
N\ случайно выбирается
число а. Найти вероятность pN того, что: а) число а
не делится ни на а19 ни на а2, где ал и а2— фиксиро
ванные натуральные взаимно простые числа; б) число а
не делится ни на какое из чисел а19 а2, . . . , ak, где
числа at — натуральные и попарно взаимно простые.
Найти lim pN в случаях а) и б).
А/ -> ОО
1.11. Из множества {1, 2, . . . , N } случайно выби
рается число а. Найти lim pN, где pN— вероятность
N -* оо
того, что а2— 1 делится на 10.
1.12. Из множества {1, 2, . . . , N } случайно выби
рается число а. Найти вероятность pN того, что а при
делении на целое число г ^ 1 дает остаток q. Найти
lim рдг.
N -*■ оо
1.13. Целое число £ случайно выбирается из мно
жества {0, 1, 2, . . . , 10"— 1}. Найти вероятность того,
что в десятичной записи это число &-значно, т. е,
представимо в виде £ = £ft- 10*-1 + £ft_ t - 10*~2+ . . .
. . . + £2. 10 + £lt где 0 < ;£ ,-s g :9 при всех i = 1, . . . , k
и I* > 0 (k > 1).
1.14. По схеме случайного выбора с возвращением
из множества натуральных чисел {1, 2, . . . , N\ выби
раются числа 1 и г]. Найти вероятность qN того, что
£ и т] взаимно просты. Найти lim qN, используя изЛ/ —► оо
V'
вестное равенство 2^
[
=
л2
п —I
1.15. По схеме случайного выбора с возвращением
из множества целых чисел {1, 2,
выбираются
числа £ и т). Обозначим p N вероятность события
; 2 - f т]2 <1 N 2. Найти lim pN.
N —► О
О
1.16. По схеме случайного выбора с возвращением
из множества целых чисел {0, 1, 2, . ., 10'*— 1} выби
раются числа § и rj. Обозначим рт вероятность того,
12
13.
что сумма %+ ц будет m-значным натуральным числомв десятичной записи. Найти вероятности p n„ k+1,
6 = 0, 1,
п, и qk= lim p n- k+1, 6 = 0, 1, 2, . . .
Л —► оо
1.17. По схеме случайного выбора с возвращением
из множества целых чисел {0, 1, 2, . . . , 10" — 1} вы
бираются числа | и г). Обозначим р т вероятность того,
что произведение
будет m-значным натуральным
числом в десятичной записи. Найти qk = lim p2n-k>
п ->■ ОО
k = 0, 1, 2, . . .
1.18. П оказать, что в задачах 1.14— 1.17 предель
ные вероятности останутся теми же самыми, если
числа | и г] выбираются из того же самого множе
ства по схеме случайного выбора без возвращения.
1.19*. По схеме случайного выбора с возвращением
из множества натуральных чисел { 1 , 2 , . . . , N }, N ^ 3,
выбираются числа X и У. Ч то больше:
Р 2 = Р { Х 2— У 2 делится на 2}
или
P S= P { X 2— У2 делится на 3}?
1.20. По схеме случайного выбора с возвращением
из множества натуральных чисел { 1 , 2 , . . . , N\, N ^ 6,
выбираются числа X и Y. П оказать, что
Р {X 4— У 4 = 0 (mod 2)} < Р { X 4— У 4 = 0 (mod 3)} <
< Р { Х 4— У4 = 0 (mod 5)}.
1.21. По схеме случайного выбора с возвращением
из множества {1, 2, . . . , N } выбираются числа X и У.
Используя малую теорему Ферма (если р — простое
Число и целое число а не делится на р, то ае-1 =
= = l(m o d p )), найти вероятность Q x(p ) того, что число
Х р~х— Ур_1 делится на простое число р. Найти
lim QN (p) = Q{p),
lim QN (p) = Q.
N — °o
p, N —*■ oo
1.22*. По схеме случайного выбора с возвращением
из множества {1, 2, . . . , N } выбираются числа X и У.
Показать, что при N ~^ 4
Р { X 3 + У3 sa 0 (mod 3)} < Р { X 3+ У3 = 0 (mod 7)}.
1.23.
Из совокупности всех подмножеств множест
ва S = {1, 2, . . . , N\ по схеме выбора с возвращением
13
14.
выбираются множества А г, А 2. Найти вероятностьтого, что А 1 (] А 2 = 0 .
1.24.
Из совокупности всех подмножеств множе
ства S = { 1 , 2 , . . . , N } по схеме выбора с возвраще
нием выбираются подмножества А 19 Л2, . . А г. Найти
вероятность того, что множества
Д2, . . . , А г по
парно не пересекаются.
1.25*. В урне содерж ится ( 2 п + 1 ) 2 карточек, на
каждой из которых написана упорядоченная пара
целых чисел (х> у) {х и у принимают значения от — п
до п, каждая пгра чисел написана ровно на одной
карточке). Из урны по схеме выбора без возвращения
извлекаются три карточки: ( l lt гц), (|2, т у , (g3, г)3).
Рассмотрим эти пары как координаты случайных то
чек S lt S 2, S 3 плоскости в декартовой системе коор
динат. Найти вероятность рп того, что 2 Х симметрич
на S 2 относительно S 3.
1.26. Брошено 10 игральных костей. Предпола
гается, что все комбинации выпавших очков равно
вероятны. Найти вероятности событий:
а) не выпало ни одной «6»;
б) выпало ровно три «6»;
в) выпала хотя бы одна «6».
1.27. Некоторые москвичи шестизначный номер
трамвайного, троллейбусного или автобусного билета
считают «счастливым», если сумма первых его трех
цифр совпадает с суммой последних трех цифр. Найти
вероятность получить «счастливый» билет.
1.28 (см. 1.27). Вычислить вероятность появления
хотя бы одного счастливого билета в случае, когда
покупается подряд п билетов, 1 < п < 9.
1.29. Из 30 чисел ( 1, 2, . . . , 29, 30) случайно отбира
ется 10 различных чисел. Найти вероятности событий!
Л = {все числа нечетные},
В = {ровно 5 чисел делится на 3},
С = {5 чисел четных и 5 нечетных, причем ровно
одно число делится на 10}.
1.30. Из урны, содержащей
шаров с номером 1,
М 2 шаров с номером 2, . . . , M N шаров с номеррм/V,
случайно без возвращения выбирается п шаров. Найти
вероятности событий:
1) появилось т1 шаров с номером 1, т2 шаров с но
мером 2, . . . , mN шаров с номером N\
2) каждый из N номеров появился хотя бы один раз.
14
15.
1.31. Из множества чисел {1, 2,по схеме
выбор . без возвращения выбираются числа
и g2.
Найти Р {Н2 >
При выборе трех чисел найти вероят
ность того, что второе число лежит между первым
и третьим.
1.32. Из множества чисел {1, 2,
N } по схеме
выбора без возвращения отобрано п различных чисел.
Расположим их в порядке возрастания: z(1) < z(2) < . . .
... < г (я). Найти вероятность того, что zim) < М < г {т+1)\
вычислить ее предел при N, М —> оо, M/N —>а £ [0, 1].
1.33. Из множества {1, 2, . . . , УУ} случайно без
возвращения выбирается k-\- \ чисел: x lf х 2, •• • ,хк+1.
Первые k чисел, расположенные в порядке возраста
ния, обозначим х а) < х 12) < . . . < х ш . Найти
Р \х ш < x k+i < XU+1)}*
1.34. Десять рукописей разложены по 30 папкам
(на одну рукопись 3 папки). Найти вероятность того,
что в случайно выбранных 6 папках не содержится
целиком ни одной рукописи.
1.35. За круглый стол рассаживаются в случайном
порядке 2п гостей. Какова вероятность того, что гостей
можно разбить на п непересекающихся пар так, чтобы
каждая пара состояла из сидящих рядом мужчины
и женщины?
1.36. Участник лотереи «Спортлото-6» на первой
карточке отметил номера (4, 12, 20, 31, 32, 33), а на
второй — (4, 12, 20, 41, 42, 43). Найти вероятность
того, что участник получит ровно два минимальных
выигрыша.
1.37. Равновероятной схемой размещения частиц по
ячейкам называют схему размещения, в которой номера
ячеек, последовательно занимаемых частицами, полу
чают посредством случайного выбора с возвращением.
Обозначим jjtr = jjt^ (n, N) число ячеек, содержащих
ровно по г частиц после размещения п частиц по N
ячейкам. Найти вероятности следующих событий:
1) |х0 (/г, Л0 > 0 (при п = N);
2) |x0 (n, Af) = 0 (при tt = i V + l ) ;
3) [х0(п, Л0 = 1 (при п== N + 1);
4) найдется ячейка, содержащая хотя бы две части
цы (при любых соотношениях между п и N).
15
16.
1.38. (См. 1,37). Найти Р {р,0 (п, N) = 0 } при произвольных п, N.
1.39. По N различимым ячейкам размещается слу
чайно п неразличимых частиц. (Элементарными собы
тиями являются наборы чисел (гх, г2, . . . , rN), где rk —
число частиц в fe-й ячейке, k — 1, 2, . . . , N .) Найти
вероятности событий:
1) р0 (пу N) > 0; 2) р0 (a, N) = 1.
1.40. В первом ряду кинотеатра, состоящем из N
кресел, сидит п человек. Предполагая, что все воз
можные размещения этих п человек в первом ряду
равновероятны, найти вероятности следующих событий:
а) An, n = {никакие 2 человека не сидят рядом};
б) Bn%N= {каждый из п человек имеет ровно одного
соседа};
в) Cn, N = { из любых двух кресел, расположенных
симметрично относительно середины ряда, хотя бы
одно свободно}.
1.41. В зале кинотеатра в первых двух рядах,
каждый из которых состоит из N кресел, сидит п че
ловек. Найти вероятности следующих событий:
а) в первом ряду никакие 2 человека не сидят рядом;
б) во втором ряду каждый человек имеет ровно
одного соседа;
в) в первом ряду из любых двух кресел, располо
женных симметрично относительно середины ряда,
хотя бы одно свободно.
1.42. Из всех отображений множества { 1 , 2 , . . . , « }
в себя случайно выбирается отображение. Найти ве
роятности событий:
а) выбранное отображение каждый из п элементов
переводит в 1;
б) элемент i имеет ровно k прообразов;
в) элемент i переводится в /;
г) выбранное отображение элементы 119г2, . .
(1 ^ ix < i2 < . . . < ik ^ п) переводит в элементы j 19 / 2, ...
. . . , j k соответственно.
1.43. Из множества всех подстановок*) степени п
случайно выбирается одна. Если элементы i19 i2, . . . , ih
различны и выбранная подстановка переводит
в l2f
i 2 а Ц» •••» ik—i а ift и ifa в tj (/j
/2
••• *
*) Подстановкой степени п называется взаимно однозначное
отображение множества {1, 2, . . . , п} на себя.
16
17.
—►ik- x —> —►tj), то говорят, что элементы iu i2, . . . , ihобразуют цикл длины k . Найти вероятности событий:
а) выбрана тождественная подстановка
б) выбранная подстановка элементы t19 £2,
ik
{h < h < ••• < h ) переводит в элементы / х, / 2, . . . , j k
соответственно;
в) элемент i в выбранной подстановке образует
единичный цикл, т. е. i —*f ;
г) элементы 1 , 2 , 3 образуют цикл длины 3: 1 —
—* 2 —►3 —►1 или 1 —> 3 —>2 —* 1;
д) все элементы образуют один цикл.
1.44
(см. 1.43). Найти вероятность Р п того, что
в случайно выбранной подстановке степени п найдется
хотя бы один цикл единичной длины. Найти lim
п -*■
1.45. Обозначим символом [1а*2аг. . . п а«] (см. [9])
множество подстановок, у которых а г циклов длины
1, . . . , а я циклов длины п (определение цикла см.
в задаче 1.43). Из множества [ l ai2a? . . . па«] случайно
выбирается одна подстановка. Найти вероятности со
бытий:
а) выбрана заранее указанная подстановка;
б) элемент i образует единичный цикл;
в) выбранная подстановка переводит i в /
§ 2. Геометрические вероятности
1.46. Случайная точка Л равномерно распределена
на отрезке [0, 1] и делит этот отрезок на две части.
Пусть гц — длина большей части и г)2— длина меньшей
части. Найти P { r h < ^ b
ПРИ любом х.
1.47 Случайная точка А имеет равномерное рас
пределение в квадрате со стороной 1. Найти вероят
ности следующих событий:
а) расстояние от точки А до фиксированной сторо
ны квадрата не превосходит х;
б) расстояние от точки А до ближайшей стороны
квадрата не превосходит х;
в) расстояние от точки А до центра квадрата не
превосходит х ;
г) расстояние от точки А до фиксированной вер
шины квадрата не превосходит х.
17
18.
1.48. Случайная точка А имеет равномерное распределение в прямоугольнике со сторонами 1 и 2.
Найти вероятности следующих событий:
а) расстояние от А до ближайшей стороны прямо
угольника не превосходит х;
б) расстояние от А до любой стороны прямоуголь
ника не превосходит х;
в) расстояние от А до диагоналей прямоугольника
не превосходит х.
1.49. Случайная точка А имеет равномерное рас
пределение в квадрате со стороной а. Найти вероят
ность того, что расстояние от А до ближайшей сто
роны квадрата меньше, чем расстояние от А до бли
жайшей диагонали квадрата.
1.50. Случайная точка А имеет равномерное рас
пределение в правильном n-угольнике. Найти вероят
ность Р п того, что А находится ближе к границе много
угольника, чем к его диагоналям. Найти такие числа С
и а, что
Р п = Спа (1 + о (1)),
п —►оо.
1.51. Случайная точка (|1? |2) равномерно распре
делена в единичном квадрате К = {{и, v): 0 ^
1,
Обозначим т] число действительных корней
многочлена / glt |2(х) = у х 3— Цх + £2.
Найти
вероят
ности
Р{П = &}, 6 = 1 , 3.
1.52. На паркет, составленный из правильных 6угольников со стороной а, случайно бросается монета
радиуса г. Найти вероятность того, что упавшая мо
нета не заденет границу ни одного из 6-угольников
паркета для:
а) 6 = 3;
б) 6 = 4;
в) 6 = 6.
1.53. Случайно подброшена монета. Будем считать,
что толщина монеты равна 0 и что вектор нормали,
приложенной к стороне монеты с гербом, при враще
нии образует конус (рис. 1). Ось конуса образует
угол 0 (— л/2 < 0 < л/2) с горизонтальной плоскостью,
а — угол между образующей конуса и его осью (0 <
< а ^ л / 2 ) . В момент падения монеты конец вектора
18
19.
нормали равномерно распределен на окружности осн ования конуса. Найти вероятность р (а, 0) того, что
монета упадет гербом вверх. При каких условиях
р(ос, 0) = 1/2?
1.54. П а р а д о к с Б е р т р а н а . В круге радиуса
R случайно проводится хорда. Обозначим £ ее длину.
Найти вероятность Q* = P {I > х\, если середина хорды
равномерно распределена в круге. Вычислить вероят
ности Q# и
того, что длина хорды больше сто
роны правильного вписанного шестиугольника и тре
угольника соответственно.
Результат зависит от того, как понимать слово
«случайно». См. задачи 1.55 и 1.56.
1.55. Решить задачу 1.54, если направление хорды
задано, а ее середина равномерно распределена на
диаметре, перпендикулярном ее направлению.
1.56. Решить задачу 1.54, если один конец хорды
закреплен, а другой равномерно распределен на ок
ружности.
1.57. На плоскость, разлинованную параллельными
прямыми (расстояние между соседними прямыми рав
но 2а), брошена полуокружность радиуса г < а; точка
(Ф, х) ( х — расстояние от центра окружности до ближай
шей прямой, 0 ^
а; ф-— угол между этой прямой и
диаметром, соединяющим концы дуги) равномерно рас
пределена в прямоугольнике [0, а ] х [ — апс/2, л /2]. Найти
вероятность того, что прямая будет иметь k (к = 0, 1, 2)
пересечений с полуокружностью.
1.58. В интервале времени [О, Т ] в случайный мо
мент и появляется сигнал длительности А. Приемник
включается в случайный момент v £ [О, Т] на время t.
19
20.
Предположив, что точка (и, v) равномерно распределена в квадрате [0, Г ] х [ 0 , Г ], найти вероятность об
наружения сигнала.
1.59. Пассажир может воспользоваться трамваями
двух маршрутов, следующих с интервалами 7\, Т 2.
Момент прихода пассажира определяет на отрезках
[О, 7\], [О, Т 2] точки и и v, равные времени, оставше
муся до прихода трамвая соответствующего маршрута.
Предполагая, что точка (и, v) равномерно распределена
на Q = {(ц, а): 0 ^ w ^ 7\, 0 ^ у ^ Т 2}, найти вероят
ность того, что пассажир, пришедший на остановку,
будет ждать не дольше t (0 < t < min (7\, Т 2)).
1.60. Однородный прямой круговой цилиндр слу
чайно бросается на горизонтальную плоскость. Найти
вероятность того, что цилиндр упадет на боковую по
верхность, если его высота /г, а радиус основания г.
Вычислить эту вероятность при h = 2r. При каких h
и г вероятности упасть на основание и на боковую
поверхность одинаковы?
1.61. Неоднородный прямой круговой цилиндр слу
чайно бросается на горизонтальную плоскость. Радиус
основания цилиндра г, центр тяжести расположен на
оси симме 1 рии цилиндра на расстоянии а от одного
основания и b > а от другого основания цилиндра.
Найти вероятность того, что цилиндр упадет: а) на
основание, расположенное ближе к центру; б) на осно
вание, более удаленное от центра тяжести; в) на боко
вую поверхность.
1.62. Однородный прямой круговой конус с высо
той h и радиусом основания г случайно бросается на
горизонтальную плоскость, а) Найти вероятность того,
что он упадет на основание; б) вычислить эту вероят
ность при r = h\ в) при каком отношении r/h эта веро
ятность равна 1/4?
1.63. Однородное тело, ограниченное сферой и
плоскостью, проходящей через центр сферы (полушар),
случайно бросается на горизонтальную плоскость.
Найти вероятность того, что полушар упадет на пло
скую часть своей границы.
1.64. Длинный однородный брус прямоугольного
поперечного сечения размера a x b , b > а, случайно
бросается на горизонтальную плоскость так, что его
ось параллельна этой плоскости, а угол поворота от
носительно этой оси равномерно распределен в [0, 2л].
20
21.
Найти вероятность того, что он упадет на более широкую боковую грань.
1.65*. На плоскости проведено п окружностей
Slt
5 „ с общим центром 0; радиус окружности Sk
равен k ( f e = l , 2 ,
Случайная точка А имеет
равномерное распределение в круге, ограниченном
окружностью 5 „; A B C — правильный треугольник, од
ной из вершин которого является А, а центром— точ
ка 0. Найти вероятность Р т того, что граница тре
угольника ABC пересекает ровно т окружностей,
т = 0, 1,
п.
Глава 2
ПОСЛЕДОВАТЕЛЬНОСТИ ИСПЫТАНИЙ
В построении математической модели последова
тельности испытаний важную роль играют понятия
независимости событий и условной вероятности. Услов
ная вероятность Р (В | А) события В при условии, что
событие А произошло, определяется формулой
Р(В\А ) = Ц $ ,
Р(Л)>0.
(2.1)
Это равенство может быть записано в виде «теоремы
умножения»
Р(А В ) = Р ( А ) Р ( В |А).
(2.2)
Обобщением (2.2) является формула
Р (Л, А 2. . . А п) = Р (Л,) Р (Л 2 \А,) Р Мз |Л, А 2) . . .
. . . Р ( А п \А1А2. . . А п_ 1).
Равенство
р (В\ А) = Р{В)
(2.3)
(2.4)
естественно интерпретировать как независимость собы
тия В от А. За определение независимости двух собы
тий А и В принимается более симметричное условие
Р( ЛВ) = Р( Л) Р( В ) ,
(2.5)
эквивалентное (2.4), если Р ( Л ) > 0 . Из (2.5) следует
независимость (см. задачу 2.15) еще трех пар событий:
Л и В, Л и В, Л и В. События Л1Э Л2, . . А п назы
ваются взаимно независимыми (или независимыми в со
вокупности, или просто независимыми), если для всех
г\
22.
комбинаций индексов 1< i2 < . . . < ik^ n (6 = 2 ,...
. . . , n) имеем
P (Л,-A v . . A ik) = P ( A h) P ( Л ,,) .. .P ( A ik).
(2.6)
Если (2.6) выполняется только при k = 2, то события
А 1У . . . , А п называют попарно независимыми; о связи
попарной и взаимной независимости см. задачи 2.19 и
2 . 20 .
В приложениях часто оказывается, что модели се
рии опытов со случайными исходами описываются либо
условными вероятностями, либо предположением о не
зависимости исходов различных опытов и заданием
безусловных вероятностей исходов. В таких случаях
по формулам (2.3) или (2.6) можно, используя задан
ные условные вероятности или независимость, вычи
слить вероятности элементарных событий.
Схема случайного выбора без возвращения (см. гл. 1)
естественно определяется в терминах условных вероят
ностей: если известен результат первых k испытаний,
то при (£ + 1 )-м испытании с равными вероятностями
может появиться любой из оставшихся элементов. Мо
дель случайного выбора, сформулированная в терми
нах условных вероятностей, совпадает с определением
из гл. 1. В терминах независимости и равновероят
ности результатов отдельных испытаний может быть
описана и схема случайного выбора с возвращением,
определенная в гл. 1.
Дадим определение последовательности испытаний.
Пусть
— {(^1> ^2» •••»^«)* ^
^» 2, . . . , N),
k = l,
2, . . . , п } .
(2.7)
Элементарное событие со = (ilt i2i . . . , in) интерпрети
руется как цепочка исходов в п последовательных ис
пытаниях, каждое из которых имеет N несовместных
исходов: 1, 2, . . . , N. Если положить
Р И = Pi,Pi, llV •-Pin I |„ I,
(2-8)
N
is_ t = 1 (s = 1 , . . . , n;
где pis и ,........is_ t > 0 , 2 pi, |/,
is= 1
ik € { l ,
l ^ f e ^ s ) , т она подмножествах множе
ства Qn однозначно определяется вероятность
р ( Л
)= 2 р и >
сое Л
22
^ £ = q „.
23.
Построенное вероятностное пространство является математической моделью последовательности п испытаний.
Последовательностью независимых однородных испы
таний является частный случай приведенной общей
модели, в которой формулу (2.8) надо заменить формулой
р (®) = P f ,/V ••/>(„
N\,
1 < Л < п ) , (2.9)
где рг + р2+ . . . + p N= 1, pt > 0, 1 = 1 ,2 ,
Определение последовательности независимых испы
таний можно дать в форме произведения вероятностных
пространств. Положим £20 = {1, 2, . . . , iV}; тогда Qn
в (2.7) можно записать в виде
Q„ = Q0x Q 0X •••х 0 0 = й о
и для любого А = Л *х А 2х . . . X Ля, где A i 9. . . , А па Q0,
имеем
Р И ) = Р ( Л 1) Р ( Л 3) . . . Р ( А Я).
Здесь Р ( Л /) = рЛ + р /я+ . . . + р ^ , если A t = : { i 19l2$ . . .
. . . , is\.
Обозначим A lq событие, состоящее в том, что в 1-м
испытании наступил исход it. Оказывается, что в моде
ли (2.7), (2.8)
P {A % \ A % A '* ...A ¥ -» \ = p n tt
w
а в модели (2.7), (2.9)
? { A ? l \ A V A % . . . A l - " } = p il.
Обозначим Bs\ событие, состоящ ее в том, что в i-м
испытании исход принадлежит множеству S f = {l£i, . . .
Л. Для независимых испытаний события В (<Л,
‘ «(г)’
*^1
В(2),
.
.
.
,
BW
о2
2>п являются взаимно независимыми при любом выборе S19 . . . , Sn.
Если
в
(2.8)
положить
pt |iu .
.
^ О,
p i] + •••+ Рлг = 11 то получится последовательность
независимых (неоднородных) испытаний, в которых ве
роятности исходов зависят от номера испытаний (но
не от результатов предыдущих испытаний).
Вероятностную модель, определенную формулами
(2.7), (2.9), называют также полиномиальной схемой.
23
24.
Обозначим через,• число появлений исхода i в п
испытаниях полиномиальной схемы. При решении за
дач полезна формула
Р
1 = тк
2=
, Ъп< N= mN) =
п\
если т{ ^ 0
(i = 1, 2, . . . , Л/) целые и л = ш1+ ш2+ . . .
... +
Частный случай полиномиальной схемы с N = 2
называют схемой Бернулли. Ниже два исхода каж
дого испытания в схеме Бернулли будем обозначать
символами 1 и 0 или называть успехом и неудачей, а
соответствующ ие им вероятности — буквами р и q =
= 1— р. Если jjt„ — число успехов (или число единиц)
в п испытаниях Бернулли, то
Р
— т\— Р п (т, р) — Cnpmqn~m, т = 0, 1, . . п. (2.11)
Если в формуле (2.11) положить р=^рп = Хп/п9 где
кп—
( 0 < А , < о о ) при п —*оо, то получим следую
щее утверждение (теорема Пуассона):
lim Р п ( т , р п) ~ ^ - К
т = 0,1,2,...
(2.12)
«1 - А . ЛЛ
Правая часть формулы (2.12) используется в прило
жениях как приближенное
значение
вероятности
Р хп = т} при больших значениях п и малых значе
ниях р. Известно (см. [2], гл. 5, § 4, теорема 8,
стр. 116), что при любом множестве В с {0, 1, 2, . . . }
Более громоздкую оценку для Р п (т, р) дает соотно
шение
24
25.
Приведем формулировки двух теорем М уавр а—Лапласа.
Локальная теорема. Если п — оо, р = const, 0 <
<Р<1, 0<
< х
=
< с2 < оо, то
У прч
«Ч . { - %
}
(i + o ^
равномерно по значениям х Пл т€ [сг, с2].
Интегральная теорема. Если п —►оо,
О < р < 1, то
o u
* )
р = const,
*{x' < ^ <x'}~ T sV 'mdu <2М
)
*1
равномерно по х 17 х 2 (— оо ^ х ± ^ х 2 ^ оо).
Правые части формул (2.13) и (2.14) дают хорошее
приближение, когда п достаточно велико, а р и q не
очень близки к нулю. Ч асто нормальным приближе
нием пользуются при npq > 20. Ошибка при исполь
зовании нормального приближения может увеличивать
ся из-за дискретности допредельного распределения
(см. задачи 2.54, 2.55). Эта ошибка может иметь по
рядок 0 ( 1 / ] / npq). Приведенные замечания очень при
ближенны и носят скорее качественный характер.
Предельное выражение в (2.14) легко можно выра
зить через значения одной из функций
X
ф (*) = - р = - j* e~“2,2du,
— ОО
X
Ф0 (х) = - у = г ^ е - “ *1Чи.
О
Для вычисления предельных выражений в (2.12) и
(2.14) можно использовать таблицы 3 и 1. Иногда в за
дачах требуется указать пределы, в которых с задан
ной вероятностью лежат значения
В этом случае
требуется находить решения уравнений 1— Ф ( х ) = а .
В таблице 2 приведены величины иа, удовлетворяющие
уравнению 1 — Ф ( ы „ ) = а . При наличии микрокальку
лятора для вычисления Ф (х ) и иа можно также поль
25
26.
зоваться приближенными формулами *)со
Р х = 2 (1 - Ф
(*)) =
j*e - W d u =
— e x n i ___(83* - f 351) х+562 \
~
Р \
п < ' л : < 5 5'
ТОЗ/ж+165
и < Х ^ Ь .э ,
( ( 4 у + 1 0 0 ) у + 2 0 5 )у *
V
((2г / + 5б ) « / + 19 2 )г/ + 1 3 1 ’
у = — \пРх ,
2 - 1 0 - 7< Р х < 1 (
в указанных интервалах значений х и Р х относитель
ная ошибка первой формулы не превышает 0,042% ,
а абсолютная ошибка второй — 0,00013. Для значений
х и Р х, лежащих вне указанных интервалов, можно
использовать приближенные формулы
п
т / 2-
Р*= V
I
Xs
я " 7 еХр \
1
2
у.
l / l(2 y + 2 8 0 )y + S 7 2 ) у
х ~
V
( ( / + 14 4) Г/ + 6 0 3
0, 94 1
(’
- ^ С С
* > 5 ’ 5’
,
’
У ~
р
1 П / *’
10~112 < Р Х < 2 - 10~7.
Во многих задачах приходится рассматривать бес
конечные последовательности испытаний. В этом слу
чае полагают
=
« * € { 1 . 2, . . . , N}\,
(2.15)
ст-алгебра событий Л порождается событиями вида
^ii> •*1п == {(^i* ^*2» •••)*
= /i> •••» ikn= jn\* (2.16)
В случае независимых испытаний
р { A t i : : : t e \ = p h . . . p , a.
(2 . 17 )
Равенства (2.17) однозначно определяют вероятность
на Л (см. [5]).
Приведем еще две формулы, полезные в тех слу
чаях, когда заданы или могут быть легко вычислены
условные вероятности. Если события В19 В 2, .
Вп
*) См.: D e r e n z o S . Е. Approximations for hand calculators
using small integer coefficients.— Math, Comput., 1977, 31, 137
214— 225.
26
27.
попарно несовместны и В1+бого события А имеем
Bn = Q, то для лю
РМ)=21Р(В*)Р(Л|Б*)
k=\
(2.18)
(формула полной вероятности) и
Р (ВтI А) =
П
Р (Дт) Р (Л 1Вт) - ,
2
т =\,
п (2.19)
р (В*) р (Л |Bft)
k—1
(формула Байеса).
§ 1. Условные вероятности
В задачах 2.1 — 2.6 вероятностное пространство
считается заданным; для вычисления условных веро
ятностей нужно использовать формулу (2.1).
2.1. Из множества чисел {1, 2, . . . , N } по схеме
случайного выбора без возвращения выбираются три
числа. Найти условную вероятность того, что третье
число попадет в интервал, образованный первыми
двумя, если известно, что первое число меньше второго.
2.2. Брошено две игральные кости. Предполагается,
что все комбинации выпавших очков равновероятны.
Найти условную вероятность того, что выпали две пя
терки, если известно, что сумма выпавших очков
делится на пять.
2.3. Из 100 карточек с числами 00, 01, . . . , 98, 99
случайно выбирается одна. Пусть гц и т]2— соответст
венно сумма и произведение цифр на выбранной кар
точке. Найти Р {rji = i\ rj2 = 0}.
2.4. Из урны, содержащей М белых и N — М чер
ных шаров, последовательно без возвращения извле
кают п шаров. Пусть Л$1) (Л ^) — событие, состоящее
в том, что i-й шар был черный (белый). Используя
классическое определение случайного выбора (гл. 1),
найти
Р {Л (Г 1)К
)4 ! ) . . . 4 5]} ,
ег. = 0, 1.
2.5. Решить задачу 2.4 в случае выбора с возвра
щением (см. введение к гл. 1, (1.3)).
2.6. Случайный выбор двух подмножеств Лх и Л2
из множества S = { 1 , 2, . . . , N\ производится так же,
27
28.
как и в задаче 1.23. Найти условную вероятностьР {\А1\= 11, |А 21= 121А г П А 2 = 0 } того, что множест
ва А х и Л2 состоят из 1г и 12 элементов соответственно
при условии, что А х и А 2 не пересекаются.
В задачах 2.7 — 2.11 предполагаются заданными
условные вероятности; при решении используются фор
мулы (2.2), (2.3).
2.7. Среди 25 экзаменационных билетов 5 «хоро
ших». Два студента по очереди берут по одному би
лету. Найти вероятность того, что:
а) первый студент взял «хороший» билет,
б) второй студент взял «хороший» билет,
в) оба студента взяли «хорошие» билеты.
2.8. Два игрока поочередно извлекают шары (без
возвращения) из урны, содержащей М белых и N-—M
черных шаров. Выигрывает тот, кто первым вынет
белый шар. И спользуя формулу (2.3), найти вероят
ность выигрыша первого участника, если a) N = 3,
М = 1; б) N = 4, М = 1 ; в) N = 6, М = 2.
2.9. Из урны, содержащей М белых и N — M чер
ных шаров, по одному без возвращения извлекаются
все шары. Используя определение случайного выбора
в терминах условных вероятностей, найти вероятнос
ти событий:
A k = { k -й шар белый},
Вкч1 = {k-й и l-й шары белые},
Ck^ = {k-й шар черный, а l-й белый}.
2.10. Из урны, содержащей 3 белых шара, 5 чер
ных и 2 красных, два игрока поочередно извлекают
по одному шару без возвращения. Выигрывает тот,
кто первым вынет белый шар. Если появляется крас
ный шар, то объявляется ничья. Пусть А г = {выигры
вает игрок, начавший игру}, А 2= {выигрывает второй
участник}, В = {игра закончилась вничью}. Найти
Р (A J , Р ( А г), Р(В).
2.11. Из урны, содержащей
белых шаров, N 2 чер
ных и N 3 красных, последовательно без возвращения
извлекают шары до тех пор, пока не появится крас
ный шар. Используя формулу (2.3), найти вероятности
следующих событий:
1) вынуто пг белых шаров и п2 черных;
2) не появилось ни одного белого шара;
3) всего вынуто k шаров.
28
29.
§ 2. Независимость событийВ задачах 2.12 — 2.16 предполагается, что задано
вероятностное пространство; требуется выяснить за
висимы или независимы некоторые события.
2.12. Брошено две игральные кости. Положим
Л£= {число очков, выпавшее на первой кости, де
лится на /},
Вг = {число очков, выпавшее на второй кости, де
лится на /},
Сг = {сумма очков, выпавших на первой и второй
костях, делится на /}.
Отправляясь от классического определения вероятнос
ти, установить, являются ли независимыми следующие
пары событий: а) Л£, B k— при любых /, k\ б) Л2, С2;
В) Л4, С4?
2.13. Игральная кость брошена 2 раза, Х г и Х 2—
числа очков, выпавшие при этих испытаниях. Р ас
смотрим события
Л1= { Х 1 делится на2, Х 2 делится на 3\,
Л2== { Х 2 делится на3, Х 2 делится на 2|,
Лз== |Х2 делится на Х 2}, Л4 = { Х 2 делится наX J ,
Ah— \Хг + Х 2 делится на 2[, Л6 = { X j+ X g делится на 3}.
Найти все пары { Л /э Лу}, тройки {Л £, А/у A k) и т. д.
взаимно независимых событий.
2.14. Случайная точка (£lf Е2) имеет равномерное
распределение в квадрате \(xlt х 2): 0 ^ х и х2^ 1 } .
При каких значениях г независимы события
2.15. События Л и В независимы. Являются ли не
зависимыми события: а) Л и В, б) Л и В?
2.16. Случайная точка £ = (£i, |2) имеет равномер
ное распределение в квадрате
1. Пусть
Показать, что любые два события из А 1У Л2, Л3 не
зависимы, но все три события А и Л2, Л3 зависимы.
Являются ли зависимыми события А гА 2 и Л3?
30.
2.17 (см. 2.16). Обобщая пример, приведенный в предыдущей задаче, показать, что для любого целого
п ^ 4 сущ ествует совокупность { Лх, . . . , Ап} событий,
обладающая следующими свойствами:
а) события А 19 . . . , А п не являются независимыми,
б) при удалении из А 1У . . . , А п любого события
остающ аяся совокупность оказывается совокупностью
независимых событий.
2.18** События А 19 А 2, . . . , А п удовлетворяют ус
ловиям
? { A i }= P t>
р | д ^ / | = P i - •-Р/.
* = 1> 2, . . . . п.
Является ли {Л х, . . . , А п\ совокупностью независимых
событий?
2.19*. П ространство элементарных событий Q со
стоит из п элементов. При каких k на подмножествах
Q можно определить вероятность Р и события А 1У . . . , A k
так, чтобы события Лх, . . . , А к были независимыми
в совокупности и 0 < Р (Л ft < 1 (i = 1, 2, . . . , k)l
2.20** П ространство элементарных событий £2 со
стоит из
3 элементов. При каких k можно так
Определить на подмножествах Q вероятность Р и со
бытия A lf . . . , A kf что Р ( Л /) > 0 (/ = 1, . . . , k) и со
бытия А 19 . . . , A k попарно независимы?
В задачах с 2.21 по 2.25 предполагается незави
симость некоторых событий; требуется вычислить ве
роятности других событий.
2.21. Упрощенная система контроля изделий состоит
из двух независимых проверок. В результате fe-й про
верки (£ = 1, 2) изделие, удовлетворяющее стандарту,
отбраковывается с вероятностью |3ft, а бракованное
изделие принимается с вероятностью a k. Изделие при
нимается, если оно прошло обе проверки. Найти ве
роятности событий:
а) бракованное изделие будет принято;
0) изделие, удовлетворяющее стандарту, будет от
браковано.
2.22. Измерительное устройство состоит из двух
приборов. Вероятность безотказной работы fe-ro при
бора за рассматриваемый период времени равна 1— a k
( й-=1, 2). Оценить вероятность того, что оба прибора
будут работать:
30
31.
а) если поломки происходят независимо;б) если ничего не известно о зависимости между
поломками этих приборов.
2.23.
Два человека купили по одной карточке л о
тереи «Спортлото-6» и независимо друг от друга отме
тили по 6 номеров. Найти вероятности событий:
а) каждый получит минимальный выигрыш;
б) каждый получит какой-либо выигрыш.
Рис. 2.
2.24.
Электрическая цепь составлена из элементов
Ak, k = l , 2, . . . , 5, по схеме, приведенной на рис. 2.
При выходе из строя любого элемента цепь в месте
его включения разрывается. Вероятность выхода из
строя за данный период элемента A k равна pk,
й = 1, . . . , 5. Предполагается, что элементы выходят
или не выходят из строя независимо друг от друга.
Найти вероятность события
С = {за рассматриваемый период
по цепи может проходить ток}.
2,25* По цели производится п независимых выстре
лов. Вероятность попадания при i-м выстреле равна
ph i = 1,
д. Найти вероятность того, что при п
выстрелах будет не менее двух попаданий.
§ 3. Формула полной вероятности
2.26.
В первой урне находятся 1 белый и 9 чер
ных шаров, а во втор ой — 1 черный и 5 белых шаров.
Из каждой урны по схеме случайного выбора без воз
вращения удалили по одному ш ару, а оставшиеся шары
ссыпали в третью урну. Найти вероятность того, что
шар, вынутый из третьей урны, окаж ется белым.
31
32.
2.27. Изделия поступают на проверку, описаннуюв задаче 2.21. Предполагая, что каждое изделие удов
летворяет стандарту с вероятностью /?, найти следую
щие вероятности:
а) вероятность того, что поступившее на проверку
изделие не будет отбраковано;
б) вероятность того, что неотбракованное изделие
удовлетворяет стандарту.
2.28. Из урны, содержащей М белых и N — М чер
ных шаров, утеряно г шаров. Сравнить вероятности
извлечения белого шара: а) до утери; б) после утери
при г = 1; в) после утери при г > 1.
2.29. Отрезок [0, а] случайной точкой делится на
две части, из которых случайно выбирается одна часть.
Обозначим г) длину выбранной части. Найти Р {т ]^ л :},
О ^ я ^ а , предполагая, что координата § случайной
точки равномерно распределена на отрезке [0, а] и ве
роятности выбора любой из полученных частей отрезка
одинаковы.
2.30. При переливании крови надо учитывать группы
крови донора и больного. Человеку, имеющему чет
вертую группу крови, можно перелить кровь любой
группы; человеку со второй или третьей группой кро
ви можно перелить кровь либо той же группы, либо
первой; человеку с первой группой крови можно пе
реливать только кровь первой группы. Среди населе
ния 33,7% имеют первую, 3 7 ,5 % — вторую, 20,9% —
третью и 7 ,9 % — четвертую группы крови, а) Найти
вероятность того, что случайно взятому больному можно
перелить кровь случайно взятого донора, б) Найти
вероятность того, что переливание можно осуществить,
если имеются два донора; три донора.
2.31. Во время испытаний было установлено, что
вероятность безотказного срабатывания реле при от
сутствии помех равна 0,99, при перегреве — 0,95, при
вибрации— 0,9, при вибрации и перегреве— 0,8. Найти
вероятность Я* отказа этого реле при работе в жар
ких странах (вероятность перегрева равна 0,2, веро
ятность вибрации 0,1) и вероятность Я2 отказа при
работе в передвижной лаборатории (вероятность пере
грева 0,1, вероятность вибрации 0,3), предполагая пе
регрев и вибрацию независимыми событиями.
2.32 (см. 2.31). Найти границы, в которых могут
изменяться вероятности Р г и Я2 в предыдущей задаче,
32
33.
если отказаться от предположения о независимостиперегрева и вибрации.
2.33. Имеется пять урн. В 1-й, 2-й и 3-й урнах
находится по 2 белых и 3 черных шара; в 4-й и 5-й
урнах— по 1 белому и 1 черному шару. Случайно
выбирается урна и из нее извлекается шар. Какова
условная вероятность того, что выбрана 4-я или 5-я
урна, если извлеченный шар оказался белым?
2.34. В стройотряде 70% первокурсников и 30%
студентов второго курса. Среди первокурсников 10%
девушек, а среди студентов второго курса — 5% деву
шек. Все девушки по очереди дежурят на кухне. Найти
вероятность того, что в случайно выбранный день на
кухне дежурит первокурсница.
2.35. По каналу связи передается одна из после
довательностей букв А А А А , В В В В , СССС с вероят
ностями р1У р2, р3 (рг + р 2+ Рз = 0- Каждая переда
ваемая буква принимается правильно с вероятностью а
и с вероятностями у ( 1 — а ) и
-^-(1— а) принимается
за две другие буквы. Предполагается, что буквы ис
кажаются независимо друг от друга. Найти вероят
ность того, что было передано А ААА, если принято
АВСА.
2.36. При рентгеновском обследовании вероятность
обнаружить заболевание туберкулезом у больного ту
беркулезом равна 1— р. Вероятность принять здоро
вого человека за больного равна а. П усть доля боль
ных туберкулезом по отношению ко всему населению
равна у.
а) Найти условную вероятность того, что человек
здоров, если он был признан больным при обследовании.
б) Вычислить найденную в п. а) условную вероят
ность при следующих числовых значениях *): 1 — р = 0,9,
а = 0,01, у = 0 ,0 0 1 .
2.37. Отдел технического контроля (ОТК) проводит
сортировку выпускаемых заводом приборов. Каждый
прибор независимо от остальных имеет дефекты с ве
роятностью р. При проверке в ОТК наличие дефектов
обнаруживается с вероятностью а; кроме того, с веро
ятностью р исправный прибор при проверке может
вести себя как дефектный. Все приборы, у которых
*) Эти значения приведены в книге: З а к с Л. Статистическое
оценивание. — М.: Статистика, 1976, стр. 49.
33
34.
при проверке обнаружены отклонения от стандарта,бракуются. Найти вероятность q0 того, что незабракованный прибор имеет дефекты, и вероятность qt того,
что забракованный прибор имеет дефекты. При каких
условиях 0о > <7i?
2.38. В урне находится 3 черных и 2 белых шара.
Первый игрок по схеме выбора без возвращения из
влекает 3 шара. Обратно он возвращает черный шар,
если среди вынутых шаров больше было черных; в про
тивном случае возвращается белый шар. Второй игрок
после этого извлекает один шар и по его цвету должен
угадывать число белых шаров среди трех шаров, вы
нутых первым игроком. Найти условную вероятность
того, что у первого игрока было: а) 0 белых, б) 1 белый,
в) 2 белых ш ара,— если второй игрок вытащил белый
шар.
§ 4. Схема Бернулли
2.39. Проведено 20 независимых испытаний, каждое
№ которых заключается в одновременном подбрасы
вании трех монет. Найти вероятность того, что хотя
бы в одном испытании появятся три «герба».
2.40. При передаче сообщения вероятность искаже
ния одного знака равна 1/10. Каковы вероятности
того, что сообщение из 10 знаков: а) не будет иска
жено, б) содержит ровно 3 искажения, в) содержит
не более трех искажений?
2.41. Испытание заключается в бросании трех иг
ральных костей. Найти вероятность того, что в пяти
независимых испытаниях ровно два раза выпадет по
три единицы.
2.42. Найти вероятность того, что в 2п испыта
ниях схемы Бернулли с вероятностью успеха р и не
удачи q = \— р п ояви тсят + п успехов и все испытания
с четными номерами закончатся успехом.
2.43. Из множества S = {1, 2, . . . , /V} случайно и
независимо выбираются два подмножества А г и А 2 так,
что каждый элемент из S независимо от других эле
ментов с вероятностью р включается в подмножество
Л/ и с вероятностью q = \— p не включается. Найти
вероятность того, что A 1 f ) A 2 = 0 .
2.44. По той же схеме выбора подмножеств из
S = {1, 2, .
N }, что в задаче 2.43, независимо вы34
35.
бцраются г подмножеств А 1У Л2, ,А п г ^ 2 . Найти
вероятность того, что выбранные подмножества попарно
не пересекаются.
2.45 (см. 2.43). Из множества S = {1, 2, .
УУ}
независимо выбираются г подмножеств А 1У Л2, . , , , А г.
Механизм выбора состоит в следующем: любой элемент
множества S независимо от других элементов с веро
ятностью Pi включается в множество А £ и с вероят
ностью q - 1 — pi не включается ( i = 1,
г). Найти
вероятность того, что подмножества A lt Л2, . . . , А г
попарно не пересекаются.
2.46 (см. 2.43). Из множества S = {1, 2,
N}
случайно и независимо выбираются подмножества
А19 . . . , А г. Механизм выбора такой же, как в зада
че 2.43. Найти: а) р|
Г) Л£- = й | ; б) р| (J А £ = &|,
где |В | обозначает число элементов множества В .
2.47. Каждую секунду с вероятностью р независимо
от других моментов времени по дороге проезжает ав
томашина. Пешеходу для перехода дороги необходи
мо 3 с. Какова вероятность того, что подошедший
к дороге пешеход будет ожидать возможности перехо
да: а) 3 с; б) 4 с; в) 5 с?
2.48. В одном из матчей на первенство мира по
шахматам ничьи не учитывались, и игра шла до тех
пор, пока один из участников матча не набирал 6 очков
(выигрыш — 1 очко, проигрыш и ничья — 0 очков). Считая
участников матча одинаковыми по силе, а результаты
отдельных игр независимыми, найти вероятность того,
что при таких правилах в момент окончания матча
проигравший набирает k очков, 6 = 0*-т-5.
2.49. Обрабатываемые на станке детали сортиру
ются по размерам на две группы. Каждая очередная
деталь независимо от предыдущих с равными вероят
ностями попадает в первую или вторую группу. Пусть
в начале смены для каждой группы деталей приготов
лено по ящику емкости г. Какова вероятность того,
что в момент, когда очередную деталь будет некуда
класть, в другом ящике будет т деталей?
2.50. По каналу связи передаются сообщения из
нулей и единиц. Из-за помех вероятность правильной
передачи знака равна 0,55. Для повышения вероят
ности правильной передачи каждый знак сообщения
35
36.
повторяют п раз. Полагают, что последовательностииз п принятых знаков в сообщении соответствует знак,
составляющий в ней большинство. Найти вероятность
правильной передачи одного знака при /г-кратном по
вторении, если п — о .
2.51 (см. 2.50). Подобрать п так, чтобы вероятность
правильной передачи знака была не меньше 0,99.
2.52. По каналу связи передается 1000 знаков. Каж
дый знак может быть искажен независимо от осталь
ных с вероятностью 0,005. Найти приближенное зна
чение вероятности того, что будет искажено не более
трех знаков.
2.53. В таблице случайных чисел цифры сгруппи
рованы по две. Найти приближенное значение вероят
ности того, что среди 100 пар пара 09 встретится не
менее двух раз.
2.54*. П усть 1п— число успехов в п независимых
испытаниях Бернулли с вероятностью успеха, равной
1/ 2 .
а) С помощью теоремы
приближенные значения
М уавра— Лапласа
найти
при п = 100.
б)
Вычислить те же вероятности, что в п. а), с по
грешностью 10-5 , используя уточненную формулу
Стирлинга.
Сравнить результаты пп. а) и б) и истолковать их.
2.55*. Решить предыдущую задачу, полагая п = 128.
2.56.
Найти приближенное значение вероятности
того, что число «девяток» среди 10 000 случайных чисел
заключено между 940 и 1060. (Случайными числами,
если не указан закон распределения, называют реали
зацию последовательности независимых испытаний
с равновероятными исходами 0, 1, . . . , 9.)
2.57 (см. 2.56). Из таблицы случайных чисел отби
рают числа, делящиеся на 3, до тех пор, пока не
наберется 1025 таких чисел. Найти приближенное зна
чение вероятности того, что потребуется таблица, со
держащая не меньше 2500 чисел.
2.58.
Театр, вмещающий 1000 человек, имеет два
разных входа. Около каждого из входов имеется свой
гардероб. Сколько мест должно быть в каждом из
36
37.
гардеробов для того, чтобы в среднем в 99 случаяхиз 100 все зрители могли раздеться в гардеробе того
входа, через который они вошли? Рассмотреть два
случая: а) зрители приходят парами; б) зрители при
ходят поодиночке. Предположить, что входы зрители
выбирают с равными вероятностями.
2.59. В поселке 2500 жителей. Каждый из них
примерно 6 раз в месяц ездит на поезде в город, вы
бирая дни поездок по случайным мотивам независимо
от остальных. Какой наименьшей вместимостью дол
жен обладать поезд, чтобы он переполнялся в среднем
не чаще одного раза в 100 дней (поезд ходит раз
в сутки).
2.60. Вероятность успеха в каждом испытании
схемы Бернулли равна р. Найти вероятность того,
что fe-й по порядку успех происходит при /-м испы
тании.
В задачах с 2.61 по 2.66 рассматриваются беско
нечные последовательности испытаний.
В оспользо
ваться частным случаем вероятностного пространства,
определяемым формулами (2.15 )— (2.17) при N = 2.
2.61. Две игральные кости бросают до выпадения
«6» хотя бы на одной из них. Найти вероятность того,
что впервые «6» появляется при fe-м бросании, k = l >
2, 3, . . .
2.62. Двое по очереди бросают монету. Выигрывает
тот, кто первым получит «герб». Найти вероятности
событий:
а) игра закончится до 4-го бросания;
б) выиграет начавший игру (первый игрок);
в) выиграет второй игрок.
2.63. В схеме Бернулли р — вероятность исхода 1
и q — 1— р — вероятность исхода 0. Найти вероятность
того, что цепочка 00, состоящая из двух нулей подряд,
появится раньше цепочки 01. В частности, вычислить
эту вероятность при р = 1/2.
2.64. Пусть выполнены условия задачи 2.63. Найти
вероятность того, что цепочка 00 (два нуля подряд)
появится раньше цепочки 10. В частности, вычислить
эту вероятность при р = 1/2.
2.65. Пусть выполнены условия задачи 2.63. Найти
вероятность Р 00|Ш того, что цепочка 00 появится
раньше цепочки 111. В частности, вычислить эту ве
роятность при р = 1/2.
37
38.
2.66. Движением частицы по целым точкам прямойуправляет схема Бернулли с вероятностью р исхода 1:
если в данном испытании схемы Бернулли появилась 1?
то частица из своего положения переходит в правую
соседнюю точку, а в противном случае— в левую.
Найти вероятность того, что за п шагов частица из
точки 0 перейдет в точку т.
§ 5. Полиномиальная схема
2.67. Отрезок [0, 10] точками 1, 2, 3, 4, 7 разде
лен на 4 отрезка длины 1 и 2 отрезка длины 3. Пусть
Лх,
Л8— независимые случайные точки, имеющие
равномерное распределение на отрезке [0, 10]. Какова
вероятность того, что из этих точек в два каких-либо
отрезка длиной 1 попадет по 2 точки, а в каждый
из оставш ихся отрезк ов— по одной точке?
2.68. При прохождении одного порога байдарка
не получает повреждений с вероятностью р х, полно
стью ломается с вероятностью р 2, получает серьезное
повреждение с вероятностью р3 (Pi + P2 + P3 = !)• Д ва
серьезных повреждения приводят к полной поломке.
Найти вероятность того, что при прохождении п по
рогов байдарка не будет полностью сломана.
2.69. Сообщения, передаваемые по каналу связи,
составляются из трех знаков А, В, С. Из-за помех
каждый знак принимается правильно с вероятностью
0,6 и принимается ошибочно за любой из двух дру
гих знаков с вероятностью 0,2. Для увеличения ве
роятности правильного приема каждый знак пере
дается 5 раз. За переданный знак принимается знак,
который чаще всего встречается в принятой пятерке
знаков. Если наиболее частых знака два, то из них
выбирается равновероятно один. Найти вероятность
правильного приема знака при указанном способе
передачи.
2.70. П усть
£— число появлений исхода i в п
первых испытаниях полиномиальной схемы (см. вве
дение к гл. 2). Найти Р {6„f l = m 1}.
2.71. В схеме, описанной в задаче 2.70, найти
условную вероятность
Р
33
2= ^2> •••>
N
= т п I 1~ ^l}*
39.
2.72. В N ячейках, разбитых на две группы поNx и N 2 ячеек соответственно (N 1+ N 2= N), незави
симо одну от другой размещают п частиц; пусть р и
(i = 1, 2; / = 1, 2,
N j ) —-вероятность попадания
частицы в / - ю ячейку i-й группы, a
— число частиц,
попавших в /-ю ячейку £-й группы после размещения
п частиц. Найти:
а) Р{Л//) = % .
i = l,2 ,
/= 1
ЛГ},
^1 I ^21
•••"Ь'ЧгЛГ, =
б) P K P + . - . + t l S ^ * . } ,
в) Р { "Hi/ == ^1/,
/ = 1,
2.73. В N ячейках независимо размещают п час
тиц. Вероятность попадания каждой частицы в i-ю
ячейку равна l/N, t = 1, 2, . . . , TV. Обозначим через
[х0 (п, Л/) число ячеек, оставш ихся пустыми. Найти
Р{[10(п, y V ) = fe }.
2.74. Игральную кость бросаю т до тех пор, пока
впервые не выпадет меньше пяти очков. Какова ве
роятность получить при последнем бросании не мень
ше двух очков?
2.75. И сходы 0Х, 02, . . . последовательности испы
таний с N = 3 возможными исходами 1, 2, 3 и вероят
ностями исходов р19 р2, р3 объединяются в тройки
Фзк+и ез*+2> ез*+з)- Из первой тройки (03v+1, e3v+2, Bsv+s).
в которой все исходы различны, выбирается 03v+iНайти P {03v+i = i}2.76. Испытания в полиномиальной схеме с исхо
дами 1, 2, 3, имеющими вероятности р19 р2, р3 соот
ветственно, заканчиваются, когда впервые не появится
исход 3. Найти вероятность того, что испытания
закончатся исходом 1.
2.77* Игрок А подбрасывает 3 игральные кости,
а игрок В — 2 кости. Эти испытания они проводят
вместе и последовательно до первого выпадения «6»
хотя бы на одной кости. Найти вероятности со
бытий:
а) А = {впервые «6» появилось у игрока Л, а не В}\
б) В = {впервые «6» появилось у игрока В, а не Л};
в) С = {впервые «6» появилось одновременно у Л
и В}.
39
40.
Глава3
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
П усть
задано
вероятностное
пространство
(£2, Л> Р).
Случайной величиной называется действительная
функция от элементарного события £ = £(со), c o g Q,
для которой при любом действительном х множество
{со: | (со )^ л ;} принадлежит Л (т. е. является событием)
и для него определена вероятность Р {со: ! ( c o ) ^ * } ,
записываемая кратко Р { | ^ а :} . Эта вероятность, рас
сматриваемая как функция х у называется функцией
распределения случайной величины § и обозначается
обычно либо F^(x)y либо F (х) (иногда функцией рас
пределения называют вероятность Р { £ < * } ) .
С помощью функции распределения F% (х) можно
однозначно определить вероятности Р { £ £ В } для борелевских множеств В на числовой прямой (определение
борелевских множеств см. в [5], гл. II, § 3, с. 32,
или в [2], гл. 2, § 1, с. 28— 29). В частности, борелевскими множествами являются интервалы вида
(х и x z]y IX» * 2]» IX» х 2)у X » * 2)» их конечные и счет
ные суммы. Вероятность Р { £ £ В } , рассматриваемая
как функция от борелевского множества В, назы
вается распределением вероятностей случайной вели
чины § и обозначается Р|(В). Иногда Р|(В) называют
законом распределения случайной величины Н или
просто распределением §. Таким образом, распределе
ние вероятностей Р|(В) можно задать функцией рас
пределения F%(x).
Важным классом распределений вероятностей яв
ляются абсолютно непрерывные распределения, зада
ваемые плотностью вероятности рg (я) = р(х)> т. е. такой
неотрицательной функцией р (,х)9 что для любого боре
левского множества В
Р {I € В} = $ Р (х) dx\
в
в общем случае рассматривается интеграл Лебега,
который совпадает с интегралом Римана (собственным
или несобственным), если последний сущ ествует. Д ру
гой класс составляют дискретные распределения, зада
40
41.
ваемые конечным или счетным набором вероятностейР Д л я
которых
2 Р { £ = * * } = !.
k
Функция распределения F|(x) в этом случае ступен
чатая и задается суммой
2
Р {& =**}
k: xk<Cx
Если распределение случайной величины абсолютно
непрерывно или дискретно, то говорят также, что
сама случайная величина или ее функция распреде
ления соответственно абсолютно непрерывны или диск
ретны.
В задачах обычно говорится о случайной величине
Ей о е е распределении Pg(-) без явного указания того
вероятностного пространства, на котором она опре
делена. Это означает, что соответствующ ее утверждение
или вычисление справедливо для любого вероятност
ного пространства (Q, Л, Р), на котором можно опре
делить случайную величину Е = £ (со) с заданным рас
пределением Р&(-); в частности, таким вероятностным
пространством^ можно считать (R , 93, Р^), где # =
—
числовая прямая, 93— борелевская ст-алгебра ее под
множеств, Р£— распределение вероятностей случайной
величины Н /к отор ая задается функцией §( x) = x.
Если на одном и том же вероятностном простран
стве (Q, Л, Р) определены случайные величины |х,
Н2, . . . , \т, то иногда говорят, что задан случайный
вектор S = ( S i , . . ! г). Многомерной функцией распре
деления (или совместной функцией распределения) §lf
|2, . . . ,
называется вероятность P {£ i^ * i>
рассматриваемая как функция от точки x = (xlt . . , , хг)
г-мерного евклидова пространства R r и обозначаемая
/ ^ . . . . . * ( * 1 , •••, %р) (кратко /^ (х )) или F (хг, - - . , х г)
(кратко F (х)). С помощью функции распределения од
нозначно определяются вероятности Р £ В}для г-мерных борелевских множеств В. Функция множеств
Р&(В) = Р { ? £ В } называется r-мерным распределением
вероятностей §. Абсолютно непрерывное г-мерное рас
пределение вероятностей задается r-мерной плотностью
P l(x)^ P h
•••» *,)• т. е. такой неотрицатель41
42.
ной функцией р%(х),множества B c : R r
что
для любого
р {S € В) = 5 . . . 5 Р\ (* 1 .
борелевского
x r)d x 1 . . . dxr.
В
Дискретное r-мерное распределение задается с помощью
конечного или счетного набора вероятностей Р {§= *(& )},
x(k) £ R ry так что для любого борелевского множества В
P { i€ 5 }=
2
ki x(k)eB
P{i = *(fc)}.
Если s-мерный случайный вектор rj есть функция
/? (!) от r-мерного случайного вектора
т. е. тц =
= g ft(Si. •••» 6r). k = l
s> g ( - ) = ( 8 i ( - ) ’ ••
. . . . g s (•)), то
P{t1€B} = P{l = g -1(В)},
где g - i ( B ) — прообраз борелевского множества В при
отображении g. В частности, если г = s = 1, функция
g (x ) непрерывна и возрастает, то
(х) = F% (g _ x (х)).
Если еще g ( x ) дифференцируема и распределение g
имеет плотность р%(х)> то распределение т] имеет
плотность
М )| -
Если г — s, отображение y = g { x ) взаимно однозначно
иякобиан J (х) = ч ^gl’
О
не обращается
(^1, .. .,gr?
Хг )
в нуль,
то плотность рц (х ) можно вычислить по плотности
Pi (х) с помощью равенства
M * ) = P 6 ( g - i ( * ) ) j r ( ^ l ( *))i'-
<з л >
Случайные величины |lt
ir называются неза
висимыми, если для любых борелевских множеств
B lt . * » , Вг имеет место равенство
P{Si€Bi, . . . . 1 г € В Л = П Р { ^ € В , } .
k= 1
Следующие определения
определению (3.2):
да
независимости
(3.2)
равносильны
43.
в общем случае: для любых х 19 . . . f x r £ Rг
•••» £/• C^i» •••> %r) ^ I I
ft=i
й
для абсолютных непрерывных распределений: для
любых * = (*!, . . . , х г) £
(кроме, может быть, точек,
образующих множество меры нуль)
г
Pi,
6г(*1. • • • .* ,) = П р Б * (**)'.
k=\
R
для дискретных распределений: для всех л: = (х1,
. . . , x r) £ R r
P { l l = X u . . . , l r = Xr\ = i i ? { l k = Xk}.
k—1
Если случайные величины
независимы,
то функции от них
=
ft= i,
А', также
будут независимыми случайными величинами.
Если | и г] — независимые случайные величины, то
по плотностям р%(х), Ръ (х) можно вычислить плотность
р|+Т1 (х) их суммы с помощью формулы композиции (или
свертки):
оо
Pg+n (х) =
оо
j Pi (у) Рп (х— У) d y = J р| (х — у) р„ (у) dy.
—ОО
—00
(3.3)
Полезны также формулы
распределения
композиции для функций
ОО
Р%+Ц (х) = J f I (X ■- у) Рп (У) dy,
(3-4)
f 6+n (*) = J F i (х — У) dFri (У)
— CO
(последний интеграл в общем случае надо понимать
как интеграл Лебега — Стилтьеса).
Математическим ожиданием случайной величины £
называется число
М£ = $ i (<o) Р (dco),
Q
43
44.
если интеграл Лебега, стоящий в правой части этогоравенства, существует (см. [5], гл. IV, § 2. с. 60 или
[2], гл. 4, § 1).
Если | имеет плотность, то ME может быть вычис
лено по формуле
оо
ME = J хр% (х) dx.
(3.5)
— 00
Для случайной
лением
величины § с дискретным распреде
ME = 2 х к? { ! = **},
k
если ряд (3.5) сходится
(3.6)
абсолютно. В общем случае
00
М l = ^ x d F l (x),
(3.7)
— 00
где интеграл понимается как интеграл Стилтьеса.
Если t] = g(E ), то для вычисления Мт) = Мg(E)
можно применять следующие формулы, аналогичные
(3.5) — (3.7) (также с оговоркой об абсолютной сх о
димости):
ОО
Mg (Е) = J g (х)
(х) dx,
(3.8)
—ОО
Mg(E) = 2 g ( * ft)P
k
(3.9)
00
Mg(E) =
<
\
) g { x ) d F l {x)
(3.10)
— оо
(в формуле (3.10) в общем случае интеграл понимается
как цнтеграл Л ебега— Стилтьеса). Формулы (3.8) —
(3.10) обобщаются на случай, когда т] = g (glt . . . , £r) —
функция, отображающая R r в R 1. В частности, фор
мула (3.8) в этом случае превращается в
Mg(Ei,
= £••
Ег) =
xr )P u ......tr (x i, - . . , x r) d x 1 . . . d x r.
(3.11)
44
45.
Для действительной случайной величины g математическое ожидание Mg* называется k-м моментом
или моментом k-го порядка, M|g|* называется абсо
лютным моментом k-го порядка, M (g — Mg)*— центральным моментом k-го порядка, M |g— Mg|* — абсолютным центральным моментом k-ao порядка. Факто
риальным моментом k-го порядка называется М|ш =
= Mg(g — 1) . . . (g—
1). Второй центральный момент
называется дисперсией и обозначается Dg = M (g — Mg)2.
Корень квадратный из дисперсии называется средним
квадратическим отклонением.
Математическое ожидание Mgr) произведения двух
случайных величин Е и г] называется смешанным вто
рым моментом. Смешанный центральный второй мо
мент М (| — Mg) (г) — Мг|) называется ковариацией слу
чайных величин g и г] и обозначается cov (g, г]). Коэф
фициентом корреляции g и г] называется отношение
р (Н, н ) = ^ = = - .
]fD tD x)
При
F
вычислении
математических
ожиданий часто используются следующие свойства:
1. Свойство аддитивности: для любых Е и т | с конеч
ными Mg и Mr)
М (g + г|) = Mg + Mr).
(3.12)
2. Свойство линейности: для любого числа с
M(cg)=cMg.
(3.13)
3. Свойство мультипликативности: для любых не
зависимых g и т] с конечными Mg и Mrj
Mgr) = MgMr).
(3.14)
С помощью этих свойств легко получаются следующие
формулы для вычисления дисперсии и ковариации:
Dg = Mg2— (Mg)2 = Mg[2] + Mg - (Mg)2,
coy (g, T ])= M gri— MgMn;
для независимых
. . . » g„
D & + . . . + i B) = s D i ft) cov (8 „ g,-) - 0
/г= 1
/).
(3 . 15)
В общем случае
D dx + . . . + У
= 2 Dg* + 2
S
cov d*. g,).
k=l
1<£</ <Л
45
46.
Если имеются две дискретные случайные величины 1и т|, то условная вероятность события
при
условии г)=*(/у определяется равенством
Р {I =
|Ц — У/} —
(3.16)
Совокупность условных вероятностей (3.16) при всех i
задает условное распределение случайной величины £
при условии т} = У у . Условное математическое ожида
ние I при условии 1
определяется формулой
м {I h = уА в 2
i
x i? ^ = * t I л ^ уА =
_ v * / P (£ = **. л = <//}
/0 17ч
(c U 7 )
Условные вероятности (3.16) и условное математиче
ское ожидание (3.17) можно рассматривать как слу
чайные величины fi(r\) = P { l = x £\i\} и g’ ('n) = М {| |г]},
которые при г] = yf принимают значения Р {£=л ;г-1 ч\=У;\
и M {i| i] = r/y} соответственно. Вычисляя математиче
ское ожидание от условного математического ожида
ния м { 5 | ч } , получаем полезную формулу
М| = М [М {| | г]}].
(3.18)
В частности,
Р {g = * , . } = МР
|ti}.
(3.19)
Для вычисления D§ можно использовать формулу
Dg = M [D {g|r|}] + D [M {6 | rin ,
(3.20)
где условная дисперсия D {£ |т]} определяется формулой
D {£ h ) = S f o — M {| | r)})aP{| = ^ |г]}.
(3.21)
Аналогичные формулы верны и для абсолютно непре
рывных распределений. Условная плотность £ при
условии 1\= у определяется формулой
/и -
ч (*’ у) _
h , л (*• у)
47.
а условное математическое ожидание — формулойоо
S хрь п {-х> у) dx
M {£|r) = i/} =
S xp l \r\=g(x)dx = - ^ - ---------------------- .
5 Pl,n(x>y)dx
— 00
Рассматривая условную плотность pi |,, (х ) как сл у
чайную величину, которая при ц = у принимает зна
чение Pi\n=g(x), получаем
ОО
М {1 h } =
S хр %\ч (х) dx>
— оо
оо
D (£ h ) =
I { х — М -{11т]})2 Pi |п (х) dx.
— оо
Формулы (3.18) и (3.20) остаются справедливыми и
в этом случае, а (3.19) заменяется формулой
(х) = Мр| \ц(х).
Общие определения условных распределений и
условных математических ожиданий можно найти
в книгах А. А. Боровкова [2] и А. Н. Колмогорова [5].
Перечислим основные способы вычисления матема
тического ожидания. При подходящем способе задания
закона распределения случайной величины наиболее
удобным может оказаться прямое вычисление по форму
лам (3.5), (3.6) или (3.8), (3.10), (3.11).
Иногда легко вычисляются или имеют простой вид
условные математические ожидания. Тогда для вычи
сления безусловных математических ожиданий исполь
зуется формула полного математического ожидания
(3.18).
Использование свойств аддитивности и мульти
пликативности математического ожидания позволяет
свести вычисление М| к более простым вычислениям
математических ожиданий величин, через которые
удается выразить £. Наиболее частым среди таких
приемов является прием введения сумм индикаторов.
Индикатором события А называется случайная вели
чина Х л ^Х л Ф )* принимающая значение 1, если cog А,
и значение 0, если со^А. Ч асто оказывается (см.,
например, задачи 3.81— 3.103), что можно указать
47
48.
такие события A lt Л2, . . . , AN, чтонас величина представляется в виде
интересующая
1 = ХА1+ ХЛ2+ •••+ 3 U y Особенно удобно то, что свойство аддитивности
верно и для зависимых слагаемых. Таким образом,
ms = 2 м 1 Ак = 2 РШ k=\
к
k= 1
Способы вычисления математических ожиданий
с помощью производящих и характеристических функ
ций рассматриваются в гл. 4.
При вычислении математического ожидания можно
пользоваться также теоремой о монотонной сходимости:{еели 1п^ 1 п+1, п = 1, 2, . . . , lim g„ = g и Mg„, Mg
П->оо
конечны, то MS = lim М|„), и теоремой о мажорируеП-*-оо
мой сходимости (если |g„ |^ т], Mr] < оо, и g = lim g„
П—
>"00
с
вероятностью
1,
то Mg =
lim Mg„). В частности,
оо
если | =
2 £»» г Де
/2= 1
и 2 М | „ сходится, то
П
ms =
2 ms„.
/2 = 1
Приведем в заключение часто встречающиеся зако
ны распределения. Сначала перечислим некоторые
дискретные распределения.
1. Вырожденное распределение:
Р {g = a | = 1,
а — постоянная.
2. Гипергеометрическое распределение (параметры:
N, М , п — натуральные числа, M ^ . N , n ^ . N ) :
Qtn Qti—tn
P {S = m} = - M
,
m==0, 1, . . . , min (M, n).
Cyv
3. Биномиальное распределение (параметры: n —
натуральное число, O ^ p ^ l ) :
P{ S = fe} = C*pft(
l
f
e
= 0, 1, . . . , n.
4. Распределение Пуассона с параметром К > 0:
P{S = /e[ = ^ e - \
48
£ = 0, 1, 2, . . .
49.
5. Геометрическоер(0<р<1):
распределение
P { l = k\ = p ( l - p ) k,
с
параметром
k = 0, 1, 2, . . .
Далее перечисляются некоторые абсолютно непре
рывные распределения, определяемые плотностью р {х).
1. Равномерное распределение на отрезке [а, &],
а<Ь:
р (х) =
,
если
a^x^Lb,
р ( х ) = 0,
если
Х ^ [а , Ь].
2. Нормальное
(или гауссовское) распределение
с параметрами а, а 2, — оо < а < оо, 0 < а < оо:
f’w=y k exp{-i£S !!}' - “ <*<“>
Нормальное распределение с параметрами (0, 1) на
зывают также стандартным нормальным распределе
нием.
3. Показательное распределение с параметром ^ > 0 :
p ( x ) = 'k e - Kx
(x ^ 0 )f
р (х ) = 0
(х<0).
4. Гамма-распределение с параметрами Я > 0, а > 0:
^ a * a -i
p ^
= ~t w
^здесь Г (a) =
(*>°)*
р (* ) = о
(*<о)
Jx a~1e~x d x — гамма-функция^ .
5. Распределение Коши с параметром b > 0:
р М = -^ тт№ >
- ° ° < х < 00-
Введем еще многомерное нормальное распределение.
Если случайные величины £lt Н2, . . . , 1Г незави
симы и имеют нормальные распределения с парамет
рами (,ak, сг|), k = l, 2, . . . , г, соответственно, то гмерная плотность нормального распределения имеет
50.
Если в (3.23) а1 = . . . = а г = 0 имы имеем плотность сферического
пределения
М * 1*
= . . . = о г = а, то
нормального рас
яу/*аг
Эта плотность инвариантна относительно ортогональ
ных преобразований пространства R r. В общем слу
чае r-мерная плотность невырожденного нормального
распределения задается формулой
B = lbkl\\— невырожденная (гх г)-м а тр и ц а , bkl =
= COV ( У i j , Ькк = co v ( У У = D y det В - определи
тель матрицы В, x — (xlt
xr), a = (alt
ar),
ak = M y Q (x) = S
квадратичная форма, когде
kf I
эффициенты которой образую т матрицу ||У||, обратную
к матрице В.
§ 1. Распределения вероятностей случайных величин
В задачах 3.1— 3.7 рассматриваются одномерные
распределения; в 3.8— 3 .24 — законы совместного рас
пределения нескольких случайных величин; в 3.25 —
3.30 — случайные величины, связанные с последова
тельностями испытаний; в 3.31— 3.38 — законы рас
пределения, заданные функциями распределения.
3.1. П лотность распределения | задана формулой
Найти: а) постоянную С; б) плотность распределения
ti = j
; в) Р{ 0, 1 < т ) < 0 , 2 } .
3.2.
Случайная величина | имеет показательное
распределение с параметром а : Р{| ^ х } = 1— е~ах (х^О).
Найти плотности распределения случайных величин:
а) % = 1 / £ ; б) т)2= | 2; в) r ^ - i - l n t ; г) т)4 = {1} ({а}—
дробная часть числа г); д) т)б = 1— е °^.
50
51.
3.3. Случайная величина | равномерно распределена на отрезке [0, 1]. Найти плотности распреде
ления случайных величин: а) г)1 = 2 | + 1 ; б) г)2 =
= — In (1 — £);
в)
r|3 = t g ( ji ( § — 1/2))}
г)
т]4 =
_ (
In 2 + Ini,
если
0 < K Va.
- \ — I n ( 1 — |) — I n 2,
если
3.4. Случайная точка В имеет равномерное рас
пределение на окруж ности х2+ (у — а)2 = г2 с центром
в точке А = (0, а), а случайная точка С = (1, 0) яв
ляется пересечением оси абсцисс с прямой, п роходя
щей через А и В. Найти функцию распределения и
плотность распределения случайной величины |. (Р ас
пределение £ называется распределением Коши.)
3.5. Показать, что если случайная величина £ имеет
непрерывную функцию распределения F {х) = Р {£
л:},
то случайная величина ri = F (| ) имеет равномерное
распределение на отрезке [0, 1]. Если же г) имеет
равномерное распределение на [0, 1], а
F -ЛУ) = s u p {х : F (х) ^ у\
(0<у<1)
— функция, обратная к функции распределения F (х)
(не обязательно непрерывной!), то случайная величина
| = Т7- ! (ту) имеет функцию распределения F (х).
3.6. П остроить пример та к ого абсолютно непре
рывного распределения случайной величины £, зада
ваемого плотностью p i(x ), ит ак о й непрерывной функ
ции g (x ), что распределение случайной величины
т) = g (1) не вырождено и дискретно.
3.7. Функция
распределения
F (х) непрерывна
в каждой точке. Д оказать, что она равномерно не
прерывна на всей прямой — оо < х < оо.
3.8. Совместное распределение случайных величин
1Х, |2 задано таблицей
\ 6.
Ех\
—1
0
1
—1
1/8
1/12
7/24
1
5/24
1/6
1/8
в которой на пересечении t-й строки и /'-го столбца
(i = — 1, 1; / = — 1, 0, 1) приведена вероятность p lt/ =
si
52.
= P { £ i = i, §2 = /} . Найти: а) одномерные законы распределения p it. = Р
= i }, p.yj = P {E2 = /} ; б) совмест
ный закон распределения qit/ = P
= i 9 r)2 = /} слу
чайных величин t ] i = £ i + £2» 'П2 = ^ 1? 2,1 b) закон рас
пределения Qit . = P {% = i\ случайной величины ц1 =
= |1 + |2; г) закон распределения q. t , = Р {rj2 = /} слу
чайной величины г]2==|1£2.
3.9.
Сумму двух независимых равномерно распре
деленных на {0, 1, . . . , 9 } однозначных чисел ^ и т]
можно записать в виде Е+ т] = 10^2+ ^ ( О ^ Е ^ Э ) .
Найти законы распределения ^ и £2. Зависимы ли
& и &
ЗЛО. Произведение двух независимых равномерно
распределенных на {О, 1, . . . , 9 } однозначных чисел
I и г) можно записать в виде !г) = 10£2+ £1, где £lf
£2— целые числа, принимающие значения от 0 до 9.
Зависимы ли
и £2?
3.11. Случайные величины Е и т| независимы и
имеют равномерное распределение на отрезке [0, а].
Найти плотности распределения случайных величин:
а) 1 + г\\ б) Е— rj; в) Егц г) Е/г).
3.12. Случайные величины § и т] независимы и
имеют показательное распределение с плотностью
е~х ( х ^ 0 ) каждая. Найти плотность распределения:
а) Ъ+ г\\ б) Е— rj; b) |Е— г| |; г) Е/г).
3.13. Найти плотность распределения суммы £ + rj,
если Е и г\ независимы, Е имеет равномерное распре
деление в отрезке [0, 1], a rj — равномерное распре
деление в отрезке [0, 2].
3.14. Найти плотность распределения суммы неза
висимых случайных величин £ и г), если Е равномерно
распределена в [0, 1], а г] имеет показательное рас
пределение с плотностью е~х ( х ^ 0 ) .
3.15. Случайные величины
Е2, Е3 независимы и
имеют равномерное распределение в [0, 1]. Найти
плотности распределения сумм а) Нх +
б) Si + ^ + Ss
и в) Р { 0 , 5 < £ 1+ |2 + |3 < 2 , 5 } .
3.16. Точка (|х, |2) имеет равномерное распре
деление в квадрате {(х, у): 0 ^ х ^ . а , О ^ у ^ а } .
П оказать, что распределения случайных величин
U i — ? 2| и niin{£i, 5а} совпадают, т. е. что для лю
бого t
=
52
£,}<*}
53.
3.17. Найти распределение суммы двух независимых слагаемых
и |2, если слагаемые распределены:
а) показательно с одним и тем же параметром а;
б) по закону Пуассона с параметрами
и Х2.
3.18. Случайные величины
независимы
и распределены показательно с одинаковым парамет
ром а. Найти плотность распределения величин:
а ) % = § 1 + • • • + £«*>
б) r|2 = min {|lt
%„}.
3.19. Найти плотность распределения
величины г) = |
случайной
, если 11У 12 независимы и равно
мерно распределены в отрезке [0, 1].
3.20. Случайные величины
|2, . . . , 1пУ
2,
независимы и имеют показательное распределение
t
с плотностью е~х ( х ^ О ) .
Обозначим
r\= g-
51
- .
Ь1 ” Г
Найти плотность распределения р^(х).
3.21. Совместное распределение
г] является равно
мерным в единичном круге х2+ У2^ 1. Найти вероят
ность Р {| S |^ 3/4, |г) |^ 3/4 }.
3.22. Величины i ly |2 независимы; P{ g 1= 0 } =
= Р
= 1} = V a, 12 равномерно распределена на от
резке [0, 1]. Найти закон распределения величины
Si +%2*
3.23. Случайная точка А = (1 1У g2, £3) £ R * имеет
равномерное распределение на сфере л:2 + у2+ 22 = 1.
Найти распределение проекций (£lt §2) и
точки А
на плоскость (ху у) и на ось х .
3.24. Пусть
§2, ^ — независимые случайные
величины, имеющие равномерное распределение на
множестве целых чисел от — п до п. Подберем мно
гочлен второй степени А (х) = а 0л:2 + а 1л: + а 2, прини
мающий при х — \у 2, 3 значения 11У £2, £3 соответст
венно. Найти вероятность Р п того, что числа а 0, а1У а 2
целые.
3.25. В схеме Бернулли с вероятностью успеха р
обозначим через тЛ(& = 2, 3, . . . ) разность номеров
испытаний, при которых происходят k-н и (k — 1)-й
успехи, а через
— число испытаний до первого успеха.
Найти совместное распределение величин xlt т2. Я в
ляются ли эти величины независимыми?
3.26. В полиномиальной схеме с исходами (1, 2, . . .
. . . , N ) вероятность t-ro исхода в каждом испытании
53
54.
равна p i9 i = l, 2, . . . , N. Положим1, если в s-м испытании появился i-й исход,
0 в противном случае.
Являются ли независимыми случайные величины:
в) es> и Ч / (s,
/ фиксированы);
б) es,;> Ч у (s=^= /);
в) &1, I» 82, г» •••> &п, ii
Г) 81, А + 81, 2^2 4" •••+ 81, МСдГ» •••> 8«, А "Ь 8п, 2^2 4“
+ . . . + e„f л/^yv» если £1# с2, . . . ,
*константы?
3.27. Игральную кость бросаю т до тех пор, пока
впервые не выпадет меньше пяти очков. Обозначим
через 0 число очков, выпавших при последнем броса
нии игральной кости, и через v — число бросаний кости.
Найти совместное распределение 0 и v. Являются ли
случайные величины 0 и v зависимыми?
3.28. В 1V ячеек независимо бросают частицы; веро
ятность попадания данной частицы в i-ю ячейку равна
p. = l/N (i = 1, . . . , N). Обозначим через хг число испы
таний до первого попадания частицы в пустую ячейку
(очевидно, %1 = 1); а через xk ( k ^ 2) — разность номеров
испытаний, соответствующ их &-му и (k — 1)-му попада
ниям в пустую ячейку; номер той пустой ячейки, кото
рая заполняется fe-й, обозначим через 0ft. Найти:
а) совместное и одномерные распределения величин
б) совместное и одномерные распределения величин
т2, т3, . . . , xN (являются ли эти величины независимыми?);
в) совместное распределение 0Х, 0 2, . . . , 0^ .
3.29. В схеме размещения частиц, описанной в за
даче 3.28 (с
найти совместное распределе
ние 0 1? . . . , 0уу.
3.30. Из урны, содержащей М белых и N — М чер
ных шаров, по схеме случайного выбора без возвра
щения вынимаются все шары. Обозначим через
число
черных шаров, извлеченных до появления Ь го белого
шара;
— число черных шаров, извлеченных между
(i — 1)-м и i-м (г = 2, . . . , М) белыми шарами, 1м+1 —
число черных шаров, появившихся после последнего
белого. Найти
а) Р { 6 != * } ;
б) P ^ f e , t 2 = l};
В) Р{^1—^1»
54
=
•**>1л1+1=
+
55.
3.31. Дана функция распределения F (х, у) парыслучайных величин £, т|. Найти Р > х, г) > у\.
3.32. Случайные величины | и г) независимы и имеют
непрерывные функции распределения. Д оказать, что
Р ^ = Т1} = 0 .
3.33. Случайные величины g, т) независимы, одина
ково распределены и имеют дискретное распределение
P { i = ^ } = p { Tl = х к\ = Рк‘ Найти Р{| = л}3.34. Двумерное распределение случайных величин
г| задано функцией распределения
Р
г] < у ) = F (х, у) =
(
О, если min (х, у) < О,
= | min (ж, у), если 0 < m i n (х, t / ) < 1,
[
если min (х, у) > 1.
Найти Р{(£ — 1/2)2+ ( л - 1 / 2 ) 2< 1 / 4 } .
3.35. П остроить пример непрерывной в точке (л;0, у0)
двумерной функции распределения
ц (х> у ), для к о
торой одномерные функции распределения Fg (х) и F^ (у)
разрывны в точках х 0 и у 0 соответственно.
3.36. П остроить такой пример непрерывной во всех
точках двумерной функции распределения
(*>*/)>
чтобы функция распределения Fglf ^ (х, у), где g ^ g + r ] ,
^ = 1 — г], имела точки разрыва.
3.37. Доказать, что двумерная функция распределе
ния F%iy](x, у) непрерывна в точке (х0, у0), если со о т
ветствующие одномерные функции распределения Ft (.х),
Ft, (у) непрерывны в точках х 0 и у0 соответственно.
3.38. Пусть случайные величины | и г] независимы,
£ имеет функцию распределения F (х), a rj равномерно
распределена в интервале [а, &]. П оказать, что £ + т|
F (х— а) — F (х — ь)
имеет плотность —
z
1------ .
Ь— а
3.39. К переговорному пункту с двумя кабинами
подошли три клиента: 1-й и 2-й клиенты заняли соот
ветственно кабины № 1 и № 2, а 3-й клиент остался
ждать. Предполагая, что времена т19 т2, т3 разговоров
клиентов независимы и распределены показательно с па
раметром К, найти: а) вероятность того, что 3-й клиент
попадет в кабину № 1; б) плотность распределения вре
мени ожидания 3-го клиента; в) вероятность того, что
3-й клиент закончит разговор раньше 1-го или 2-го
клиентов.
55
56.
3.40. В переговорном пункте телефоны-автоматырасположены в трех залах: в i-м зале п( автоматов
(i = 1, 2, 3; п = пг + п2+ п3). После перерыва посетители
одновременно заняли все автоматы. Введем события
А; = {посетитель, закончивший разговор первым, нахо
дился в f-м зале}, i = 1, 2, 3. Найти вероятности собы
тий A it i = 1, 2, 3, если времена разговора посетителей
являются независимыми одинаково распределенными
случайными величинами с непрерывной функцией рас
пределения.
3.41. Случайная величина § с равномерным рас
пределением на [0, 1] записывается в виде бесконечоо
ной десятичной дроби:
где 1„ — целые,
п —1
0 < 1 П< 9 . Д оказать, что случайные величины £lt 12, . . .
независимы.
П усть l x, 12, . . . , 1„ — независимые одинаково рас
пределенные случайные величины. При каждом со ££2
расположим числа l*(w ), k = l,
п, в порядке воз
растания и перенумеруем их заново: 1 (1 ) ^ 1 (8)<
^ ...
Полученная последовательность случай
ных величин называется вариационным рядом, а сами
случайные величины |ш — членами вариационного ряда.
Таким образом, в частности, 1Ш = min l ft, 1<„, = m a x l ft.
1
1< fe< n
Задачи 3.42— 3.48 связаны с вариационным рядом.
3.42. Случайные величины |1, |2, .
(п ^ 2 )
независимы и одинаково распределены с функцией
распределения F (х). Найти: а) функцию распределе
ния 1(1); б) функцию распределения 1(„,; в) двумерную
функцию распределения 1Ш, |(„,.
3.43. По независимым одинаково распределенным
случайным величинам 1Х, .
имеющим функцию
распределения F (х) и плотность р (х), построен вариа
ционный ряд l (i) < 1(2, < . . . < !<„,. Найти: а) плотность
распределения
б) совместную плотность распре
деления 1ш и l (m, (k < т).
3.44. Случайные величины 1ц . . . , l ft, l ft+1 незави
симы и имеют одну и ту же непрерывную функцию
распределения. П усть l (i , < l (2) < v • < 1 (й, — вариаци
онный ряд величин 1ц . . . , l ft. Найти
Р {ift+i 6 [5ц)> l(i+i)]}> l —
Р
56
^ £(»}>
. •-1 k
Р {£ft +l ^ £<*)}
1,
57.
3.45. Случайные величины |1#независимый
имеют одинаковое распределение с плотностью р (х ).
Найти м-мерную плотность р п (х 19 . . . , * „ ) распределе
ния членов вариационного ряда Еш , |{2), . . . , | (п).
3.46. Случайные величины Е1? |2, . . . , £„ независимы
и имеют показательное распределение с параметром а:
Р { Е / < 4 = 1 - е " аА>
О,
i = l,
/г,
а |(1)< | (2)< . . . < ? ( „ ) — значения
распо
ложенные в порядке неубывания (вариационный ряд).
Показать, что случайные величины
^ / = 5(/)
5(/-i)»
i = 2, . . . , / i ,
P { A I. < x } = l - r (X(n- l'+1)x,
i = lf ...,n.
независимы и что
3.47*. Случайные величины Elt |2, . . . .
незави
симы и имеют одно и то же показательное распреде
ление с параметром К. Доказать, что случайные ве
личины
m a x f o , gt. . . . , U
g1 + i i + * i + . . . + k
и
одинаково распределены.
3.48. П усть £„ = (£„, 1ч •••, £«,*). п = 1, 2, . . . , —
последовательность независимых векторов, у которых
координаты
и ...,
^— независимые случайные
величины, имеющие одну и ту же непрерывную функ
цию распределения F (х). Положим
Л„ = /£ „, / <
\
min |Я11.,
1< т < п
i=
J
Доказать, что при k ^ 2
РI U
Iп— 2
I
< — !— .
3.49*. Случайная величина
кону П уассона с параметром
=
2*-»-3
распределена по за
Л= 0, 1, 2 ..........
а случайная величина | 2 распределена по закону
П уассона с параметром К2 >
Доказать, что при
любом целом k
57
58.
3.50.Функции распределения
летворяют условию
(t) и F 2 (t) удов
Fi (0 ^ F 2 (t) для любого t.
П оказать, что можно так задать на одном вероят
ностном пространстве случайные величины
и 12
с функциями распределения
(t) и F 2 (t) соответст
венно, что
3.51.
Случайные величины 1 и г) независимы и
имеют равномерное распределение на отрезке [ 0 , 1 ],
а случайная величина £ удовлетворяет условиям
Найти максимально и минимально возможные значеуказать, при каких совместных
распределениях £, т] и £ эти значения достигаются.
3.52.
Случайные величины | и г) независимы и
имеют одно и то же распределение с непрерывной
функцией распределения F (х), а случайная величина
£ удовлетворяет условиям
Р{£ = | > = Р { £ = г,} = 1- .
П усть mg = su p {x : P { £ ^ x } ^ V 2} — медиана распреде
ления £. Найти минимальное и максимальное значе
ния
и указать, при каких совместных распреде
лениях |, г) и £ эти значения достигаю тся.
3.53,
П усть
X , Y — независимые
целочисленные
случайные величины, Z = X -\-Y,
a = m in {n : P {Z = n } > 0 } ,
b = max {n: P { Z = n } > 0 [ .
Д оказать, что
m in {P { Z = a } ,
Р {Z = 6 }}
Т ,
§ 2. Математические ожидания
Задачи 3.54— 3.60 содержат полезные для решения
последующ их задач формулы для математических ожи
даний различных функций от случайных величин,
58
59.
в задачах 3.61— 3.80 используются прямые способы вычисления математических ожиданий, задачи 3.81— 3.103
иллюстрируют возможности метода индикаторов (см.
введение к гл. 3), в задачах 3.104— 3.124 используются
различные методы вычисления и оценок математиче
ских ожиданий, а само понятие математического ожи
дания применяется для решения вероятностных задач.
Последняя группа задач (3.125— 3.132) связана с ма
тематическими ожиданиями функций от зависимых
случайных величин.
3.54. Случайная величина X принимает только
целые неотрицательные значения. Доказать, что
оо
м х = 2 p {x^ k \ .
fe= l
3.55. Случайная величина X принимает только
целые неотрицательные значения. Д оказать, что для
любого целого k ^ 2
оо
MX ( X - l ) . . . ( X - f t + l ) = f t 2
n—1
n[ft- 1]P { X > n } .
3.56. П усть Л1( Л2, . . . — совокупность событий,
X,- — индикатор события Л,- (г = 1 , 2 , . . . ) , т. е.
если событие
Н
о
происходит,
в противном случае,
и 5 = X i + X2 + * - - — число одновременно происходя
щих событий из Л1? Л2, . . . Доказать, что
3.57*. Неотрицательная случайная
имеет функцию распределения
величина
1
Доказать, что
M l = 5 (1 — F {x ))d x .
59
60.
3.58. Случайная величина | имеет функцию распределения F (х) = Р {I ^ х}. Д оказать, что
оо
О
М| = ^ (1 — F ( x ) ) d x — J F ( x ) d x .
О
—00
3.59. Неотрицательная случайная величина £ имеет
функцию распределения F (х) = Р ^ х\. Доказать,
что для любого действительного а ^=0
оо
М|а = Iа |5 Xе*-1 (1 - F (х)) dx.
О
3.60. Случайная величина £ имеет функцию рас
пределения F (х)
{ Ъ ^ х \ . Показать, что если
F -i (y)~ su p {x: F W < y } ,
то для любой интегрируемой функции h(x)
1
М ( Ъ ) = 5 h { F _ t (y))dy.
О
3.61. Совместное распределение У | 2 определяется
условиями Р { М 2 = 0 >= 1 , p {^i = H = p { E i = — 'Ц = 1 и>
i = 1, 2. Найти М У Mg2, Dglf Dga, c o v ( y ga).
3.62. Случайная величина £ равномерно распреде
лена на отрезке [0, 2л]; T j ^ c o s i , r]2 = sin|. Найти
cov (r)i, т]2). Являются ли % и т|2 независимыми?
3.63. Случайная точка А имеет в круге радиуса R
равномерное распределение. Найти математическое
ожидание и дисперсию расстояния § точки А от центра.
3.64. Случайные величины У У . . . независимы
и одинаково распределены:
Р ^ . = 1} = Р {| (. = - 1 } = 1/4,
р {£*=0} = 1/2, ; = 1 , 2, . . .
Найти математическое ожидание и дисперсию сл у
чайной величины S„ = £i + . . . + У
3.65. Случайные величины е 1Уг2, . . . независимы и
одинаково распределены:
а &£ =5=
60
Р { е , = 0 } = Р {е (= 1 } = 1 / 2 ,
В/+2» i = 1 , 2 , « « f
t = 1 , 2 .........
61.
а) Показать, что случайные величины 6г, 62, . . .распределены так же, как
случайные величины
|х, £2, . . . в задаче 3.64, и что при любом г = 1 , 2 , . . .
случайные величины 6 £. и 6£.+1 независимы.
б) Найти математическое ожидание и дисперсию
случайной величины R n = 81 + . . . + 6 Л,
2.
3 . 66. Найти М£, D|,
# если:
а) Р
=
=
б)
=
=
m = 0, 1 , 2 , . . . ;
9 = 1 — р, т = 0, 1, .
п.
3.67. Случайные величины £2,
независимы
и равномерно распределены в отрезке [ 0 , 1]. Найти
P { 6i + i 2+ •••+ £ « < * } при 0 < х < 1 .
3 . 68. Случайные величины £1Э Е2, . . . независимы
и равномерно распределены в отрезке [0, 1]. Опреде
лим случайную величину v равной тому значению k ,
при котором впервые сумма Si + S2+ • • • + !* превзой
дет 1. Найти Mv.
3.69. Случайные величины 11У
независимы;
DН; = ст?, i = l, . . . , п . При каких с19 .
удовлет
воряющих условиям ck^ 0 , сг + . . . + с „ = 1 , случайная
величина r]„ =
+ ... +
имеет
минимальную
дисперсию? Найти минимальную дисперсию.
3.70. По известному «правилу трех сигм» вероят
ность отклонения случайной величины от своего мате
матического ожидания более чем на три корня из
дисперсии мала. Найти Р {|£ — Mg |< 3 ] / d I }, если g
имеет:
а) нормальное распределение;
б) показательное распределение;
в) равномерное распределение на отрезке Г— 1 , 1 1 ;
г) р { | = - 1 } = р ц = 1 } = > /18, Р { 1 = 0 } = % ;
д) распределение Пуассона с Mg = 0,09.
3.71. Случайные величины g, ц (возможно, зави
симые) обладают конечными дисперсиями:
Dg = c^,
Drj = o|. Указать пределы, в которых может изменяться
0 ( 1 + г\).
3.72. Случайные величины g1? . . . , gn, г^, . . . , г\п
независимы. Положим
\>п= £i + ••• +
£/* = ^irh + ••• +
61
62.
Найти М£„, М &, D£„, D£*, cov (£B, £ ) , если:Mg* = a,
р {Ла=1}=Р»
D ^ = a2,
Р{Лл = 0 } = ^ = 1 — p.
3.73. В экспедиции, рассчитанной на п дней, еже*
дневно от запаса продуктов нужно отделять соответствующ ую часть: в 1 -й день l/n -ю часть, во 2 -й день —
от остатка 1/{п— 1)-ю часть и т. д. В действительности
нужная часть продуктов отделяется с ошибкой. Пусть
r\k (k = l , 2 , . . . , n — 1 ) — часть от остатка продуктов,
которая отделяется в &-й день. Предполагается, что
величины г)А независимы, hAr\k = ak =
t - Найти
математическое ожидание случайной величины, рав
ной части продуктов, оставшейся к последнему дню:
5= 0 —%)0 —л.) -•-(1—л»-х)3.74. Вычислить математическое ожидание и диспер
сию определителя A = |
| к *. / < „ , элементы которого
— независимые случайные величины с M ! l7 = 0 и
Ь|17 = сг2.
3.75. П усть матрица S = \ \ l f y ||?, /==1, где
. . . , 1п—
независимые случайные величины, имеющие симмет
ричные распределения (т. е. распределение h совпа
дает с распределением — !,-, i = 1 , . . . , п). Показать,
что если М 1 |* < оо, i = 1 , . . . , п , для целого k ^ 1 ,
то M S*-—диагональная матрица.
3.76. Неотрицательная случайная величина § имеет
монотонно убывающую выпуклую вниз плотность рас
пределения f ( x ) t f " ( x ) > 0. Что можно сказать о зна
ках величин Ms i ng , M co s| ?
3.77. Обозначим т)„ = max {|i„, п — [лп}, где \хп —
число успехов в схеме Бернулли с п испытаниями и
с вероятностью успеха р. Найти lim n_ 1Mr]w.
п
-
оо
3.78. П усть (Е, г)) — координаты случайной точки,
имеющей равномерное распределение в области D с R z.
Найти коэффициент корреляции р(|, rj), если:
а) D — часть единичного круга, лежащая в первом
квадранте: я 2 + */2
1 , х ^ О , у ^ 0;
б) D — треугольник: х + у ^ . 1 , х ^ О , у ^ 0.
3.79. По последовательности
|г, . . . испытаний
Бернулли (Р {Е ,= 1} = р > 0, Р{^. = 0} = ^ = 1 — р > 0,
Sa, . . . независимы) построим последовательность
62
63.
пар (§!, у , (|3, g4), . . . и вычеркнем из этой новойпоследовательности все пары вида (0, 0) и (1, 1). Для
f e = l , 2 , . . . положим
равным первому члену k-й
невычеркнутой пары.
а) П оказать, что гц, т]2, . . . — последовательность
независимых случайных величин.
б) Найти математическое ожидание числа v членов
исходной последовательности, использованных для
того, чтобы определить значение % .
3.80. По той же последовательности %1У У
что в задаче 3.79, построим последовательность троек
( У У У > ( У У У » ••• и вычеркнем из нее все
тройки вида (0, 0, 0) и (1, 1, 1). Для f t = l , 2, . . .
положим ц к равным 1 , 2 или 3 в соответствии с но
мером того члена k-й невычеркнутой тройки, который
отличается от двух остальных.
а) П оказать, что % , rj2, . . . — последовательность
независимых случайных величин, Р \y\k = i\ = 7 3, i = 1,
2 , 3, для k = 1 , 2 , . . .
б) Найти математическое ожидание числа членов
исходной последовательности, использованных для
того, чтобы определить значение гц.
3.81. Обозначим через 0Г число циклов длины г
в подстановке, случайно выбранной из множества
всех п\ подстановок степени п. Найти: a) M0lf D0X;
б) М02; в) M0r
1).
3.82. В урне содержится М г шаров с номером 1 ,
М 2 шаров с номером 2, . . . , M N шаров с номером N.
По схеме случайного выбора без возвращения выби
рается п шаров. Найти математическое ожидание
числа непоявившихся номеров.
3.83. Из урны, содержащей М белых и N — M
черных шаров, по схеме выбора без возвращения из
влекается выборка объема п. Число белых шаров §
в выборке имеет гипергеометрическое распределение:
г т г п-т
р|| = /и} = С« С* - М . Найти М | и
Cn
3.84. Из урны, содержащей М белых и N — M чер
ных шаров, по схеме случайного выбора без возвра
щения вынимаются все шары. Обозначим через
число
шаров, извлеченных до появления 1 -го белого шара
(включая этот шар), через т,- — число шаров, извле
ченных после (£ — 1 )-го белого до появления i-ro белого
63
64.
включительно, t m+1 — число шаров, извлеченных послеУИ-го белого шара. Найти Мт,-.
3.85. В N ячейках случайно размещаются п частиц.
Каж дая частица независимо от остальных с вероят
ностью 1/N может попасть в любую фиксированную
ячейку. Обозначим через p0(n, N) число пустых ячеек.
Найти M p0(n, N), Dp0 (п, N) и асимптотические фор
мулы для них при riy N —►оо, n/N - ^ а £ ( 0 , оо).
3.86. В группе учится 25 студентов. Предполагая,
что дни рождения студентов независимы и равномерно
распределены по 12 месяцам года, найти математи
ческое ожидание и дисперсию числа месяцев, на ко
торые не приходится ни один день рождения.
3.87. Для случайной величины \i0(n9 N), опреде
ленной в задаче 3.85, найти М (р0 (n, N))lk] при k = \ ,
2, . . . и lim М (jji0 (n, N ))m при п, N —►оо,
— l n N —
—* ln-^-, 0 < К < оо.
3.88. По N ячейкам случайно размещаются п не
различимых частиц. Все размещения равновероятны.
Обозначим через рг число ячеек, содержащих ровно
г частиц. Для Мр,. найти точную формулу и асимпто
тическую формулу при п, N — оо, n/N —> а £ ( 0 , оо).
3.89. П усть £и. — число появлений £-го исхода
в п независимых испытаниях с N несовместными ис
ходами и вероятностью ру- появления /-го исхода в
s-м испытании (/ = 1, . . . , N\ s = 1, . . . , п\ р 1+ - * . +
+ pN = 1). Найти: а) М£„,
б)
в) cov (£„, „
у)
( » Ф /)
3.90. Сопоставим описанной в задаче 3.89 после
довательности п независимых испытаний процесс раз
мещения п частиц по N ячейкам, интерпретируя
появление /-го исхода в fe-м испытании как попадание
&-й частицы в /- ю ячейку. Обозначим через рг =
--^pr (n; p lf . . . , pN) число ячеек, в которых после
размещения п частиц оказалось ровно по г = 0, 1, . . .
частиц. Найти: а) Мр0; б) М р/, в)
min Мр0 (п\
pN
Р1. •••. Pn )
3.91. В N ячейках последовательно размещают
частицы. Каж дая частица независимо от остальных
попадает в любую фиксированную ячейку с вероят
ностью 1IN. Обозначим через vk минимальный номер
и
65.
частицы, после размещения которой число занятыхт. е. не пустых) ячеек станет равным k. Найти Mv^,
>Vfc и асимптотическую формулу для MvN при N —* оо.
3.92. По маршруту ходит N автобусов без кон
дуктора. В каждом автобусе имеется касса, в которой
перед выходом в рейс было г билетов. Всего эти авто
бусы перевезли п пассажиров. Найти математическое
ожидание числа § пассажиров, которым не досталось
билетов, предполагая, что каждый пассажир незави
симо от остальных может сесть в любой из автобусов
с одной и той же вероятностью 1/N.
3.93. В партии п изделий, каждое из которых не
зависимо от остальных с вероятностью р удовлетво
ряет стандарту, а с вероятностью q = l — р — не удов
летворяет ему. Изделия проходят проверку, описанную
в задаче 2.21. За каждое изделие, удовлетворяющее
стандарту и прошедшее проверку, предприятие полу
чает а рублей; за изделие, прошедшее проверку, но
не удовлетворяющее стандарту, уплачивается штраф
b рублей; за изделие, не прошедшее проверку (забра
кованное), уплачивается штраф с рублей. Найти мате
матическое ожидание прибыли предприятия, получен
ной за партию из п изделий.
3.94. Два участника лотереи «Спортлото-6» купили
по 7 карточек. Первый участник выбрал 7 различных
номеров и образовал из них семь различных шестерок
номеров, которыми заполнил карточки. Второй участ
ник выбрал 42 различных номера и заполнил карточки
так, что любые две не имеют общих номеров. Обозна
чим через
(fe= 1, 2) число карточек fe-ro участника,
на которых ровно по 3 номера совпали с номерами,
выигравшими в тираже. Найти М % , Mr]2, Dr^, Dt]2,
Drjj/Drjg.
3.95. Продано п карточек лотереи «Спортлото-6».
Обозначим
i число карточек, на которых угадано
ровно i номеров (i = 0, 1, . . . , 6). Найти
,,
Найти вероятность того, что хотя бы на одной кар
точке будут угаданы все номера. Рассмотреть два
случая:
а) Все проданные карточки заполняются равно
вероятно и независимо.
б) Каждый из т участников имеет г карточек,
которые он заполняет одинаково, но независимо от
остальных участников, п = тг.
!
65
66.
3.96. На бесконечный лист клетчатой бумаги (сторона клеточки равна 1) случайно бросается круг
единичного радиуса. Считая, что центр круга равно
мерно распределен на том единичном квадрате, на
который он попал, найти математическое ожидание
числа | точек с целочисленными координатами (х , у),
покрытых этим кругом.
3.97. К аж дую целочисленную точку числовой оси
независимо от остальных назовем белой с вероятно
стью р и черной с вероятностью < 7 = 1 — р. П усть S —
множество всех таких целочисленных точек х, что
расстояние от х до ближайшей черной точки (вклю
чая х) не меньше расстояния от х до начала коорди
нат. Найти математическое ожидание числа |S| эле
ментов множества S.
3.98. Точки Сх, . . . , Сп независимы и имеют рав
номерное распределение в круге К с центром О и
радиусом 1. П усть случайное множество А состоит
из тех и только тех точек круга, которые находятся
ближе к центру О, чем к границе круга и к любой
из точек Си . . . , Сп. Найти математическое ожидание
площади 1 множества А.
3.99. На плоскость независимо брошено N кругов
радиуса г так, что центры этих кругов равномерно
распределены в круге радиуса R. Обозначим через
площадь множества точек плоскости, покрытых ровно
т кругами. Найти
если
3.100. в схеме Бернулли с п испытаниями и с ве
роятностью успеха р и вероятностью неудачи q = 1— р
найти асимптотические формулы (при п —* оо) для
математического ожидания и дисперсии числа р,00
появлений цепочек НН из двух неудач подряд (мы
будем считать, что при i-м испытании появилась це
почка НН, если при (t — 1)-м и при i-м испытаниях
были неудачи).
3.101. В схеме Бернулли задачи 3.100 найти асимп
тотические формулы (при п —>оо) для математического
ожидания и дисперсии числа [л1П появлений цепочек
У У У из трех успехов подряд (мы будем считать, что
при i-м испытании появилась цепочка У У У , если при
(i — 2)-м (i — 1)-м и i -м испытаниях были успехи).
66
67.
3.102. П усть проведено п испытаний по той жесхеме Бернулли, что в задачах 3.100, 3.101. Считая
для удобства, что дополнительные испытания с номе
рами 0 и п + 1 закончились неудачами, введем поня
тие серии успехов как такой цепочки последователь
ных испытаний, в которой каж дое испытание за
кончилось успехом, а испытание, предшествующее
цепочке, и испытание, следующее за ней,— неудачей.
Пусть т]„ — число серий успехов в последовательности
п испытаний
Бернулли.
Найти:
а)
Р { = 0};
б) Р{Л„ = 1}; в) Мг|„; г)
n - ‘ Dr)n.
3.103. Из 30 чисел (1, 2, . . . , 29, 30) по схеме
равновероятного выбора без возвращения отбираются
10 чисел. Найти математическое ожидание суммы
выбранных чисел.
3.104. П усть §!, Е2, . . . , 1п — независимые случай
ные величины, имеющие равномерное распределение
на отрезке [0, 1], а
••
построен
ный по
вариационный ряд, т. е. значения
In •••, Еп’ расположенные в порядке неубывания. Найти
плотность р {(х) распределения §(i),
(fe= 1, 2, . . . ) ,
3.105. П усть i (1)
|(2) ^
^ |(n) — вариационный
ряд, построенный по независимым случайным вели
чинам
...,
имеющим равномерное распределе
ние на отрезке [0, 1] (см. задачу 3.104). Найти кова
риацию и коэффициент корреляции £</> и £ф. При
каких условиях lim р СЕ</>. !</>) — 0?
п—
Уоо
3.106. П усть £ = (£lt . . . ,
чайная величина. Д оказать,
1 = 1 , . . . , k, то
что
— векторная сл у
если М |£; | < о о ,
|М £\<М |£|.
3.107. П усть £ = £ + 1т]— случайная величина, при
нимающая комплексные значения. Д оказать, что если
М | | | < о о , М |г] |< оо, то | M £ K M | £ | .
3.108. П усть £х, £2, . . . , £„ — случайные величины
с нулевыми математическими ожиданиями и единич
ными дисперсиями. Д оказать, что если все эти вели
чины одинаково коррелированы, т. е. р(£/, %j) = C
при любых 1, / € { 1 > •••» п\, 1 ф } , то С ^
Т т -.
67
68.
3.109*. Д оказать, что если М |Ц А< о о , тоlim х кР {| £ |> л:} = 0 .
X—
*• оо
3.110. Независимые случайные величины
...,
положительны и имеют одинаковое невырож
денное
распределение.
Обозначим
r\k a g-b i “r •••t
.
Sb
Наити: а) математическое ожидание r)k; б) коэффи
циент корреляции у]к и г)г; в) коэффициент корреляции
%+•••+% и % +...+!!,.
3.111. Найти на прямой такую точку В , чтобы
математическое ожидание расстояния между ней и
случайной точкой Л, распределение координаты g
которой имеет непрерывную плотность, было мини
мальным.
3.112. Случайные величины
ц имеют непрерыв
ную совместную плотность распределения. Как вы
брать точку В = (х, у) £ R 2> чтобы функция ф (х, у) =
= М {|
-*| + |г] — у\\ была минимальной?
3.113. Случайная величина § имеет конечный вто
рой момент М£2. Найти m in M (| — х )2 и то значение х ,
л:
при котором этот минимум достигается.
3.114. Будем говорить, что случайная величина g
сосредоточена на отрезке [а, &], если Р { а ^ | ^ & } = 1
и при любом е > 0
Р {а < !< а + е}>0
и Р{Ь — е < | < Ь } > 0 .
Д оказать, что дисперсия случайной величины, сосре
доточенной на отрезке длины /, не превосходит / 2/4.
3.115. Доказать, что если случайные величины r\lt
т]2 независимы и
сосредоточена на отрезке длины lh
i = 1, 2, то сумма ти + ть сосредоточена на отрезке
длины / = /г + /2.
3.116. Говорят, что случайная величина g имеет
безгранично делимое распределение, если при любом
натуральном п ее можно представить в виде суммы
%i + •••+ %п независимых одинаково распределенных
случайных величин. Д оказать, что невырожденное
безгранично делимое распределение не может быть
сосредоточено на конечном отрезке.
3.117. П усть вероятностное распределение Р на
плоскости R 2 таково, что если точки Х 19 Х 2, X 3 € R 2
68
69.
независимы и имеют распределение Р, тоР { Х 4, Х 2, Х 3 лежат на одной прямой}-= 0.
Показать, что если точки X lt Х 2, X 3 g / ? 2 независимы
и имеют распределение Р, то
Р3 = Р {один из углов Д Х 1Х 2Х В не меньше 1 20°}^ 1/2 0.
3.118. П усть вероятностное распределение Р на
плоскости такое же, как в задаче 3.117. П оказать,
что если точки Х 19 Х 2, Х 3, Х 4 £ Р 2 независимы и
имеют распределение Р, то
Р4 = Р { Х х, Х 2, Х 3, Х 4 образуют
выпуклый четырехугольник}
1/5.
3.119. Показать, что если £ — действительная сл у
чайная величина с конечным математическим ож ида
нием и / (х) — функция, выпуклая вниз, то
м ш > / ( M g)e
а если f (.х) выпукла вверх, то
м / a x f (M l).
3.120. Показать, что для любых случайных вели
чин glt g2, . . . , \к с конечными r-ми ( г ^ 1 ) момен
тами справедливо соотношение
3.121. Д оказать,
неравенство
что
при
1 ^ г^ 2
\х-\-у\г -\-\х — </|г ^ 2 ( |д:|г + 11/ |г),
справедливо
— оо < * , у < оо,
и с его помощью показать, что если случайные вели
чины | и т] независимы и распределение т] симмет
рично (т. е. распределения т) и — rj совпадают), то
при любом г, 1 ^ г ^ 2 ,
3.122. П оказать, что если случайные величины
независимы, имеют симметричные распре
деления и М 11(- |г < оо, t = l , . . . , п, для некоторого
г £ [ 1 , 2], то
M|S1+ . . . + U ' < M | g 1| ' + . . . + M | g B|'.
69
70.
3.123*. П оказать, что если случайные величины| и т] независимы, Мг} = 0, и М|£|г < о о , M|tj|r < o o
для н екоторого действительного г ^ 1 , то
M |g + r ||'> M |5 |'.
3.124. И спользуя задачи 3.120— 3.123, доказать,
что если |х, . . . ,
— независимые случайные вели
чины, М1,- = 0, М 1 | г < оо, i = l , . . . , п, для некото
рого г, 1 ^ г ^ 2, то
|г + . . . + М | Е в Ю-
3.125. Случайный вектор E= (£i>
Еа) прини
мает значения в R k, и существует такой набор чисел
(оь0, a lf
a k) Ф (О, 0,
0),
что Р { а ^ Л - . . . + a*E* + a 0 = 0} = 1. Доказать, что
если все элементы матрицы ковариаций В = [|°г/у II ком
понент вектора Е конечны, то:
а) d etB = 0;
б) (alf
a k) B = B ( a u . . . , a ft)T, где т _ ЗНак
транспонирования.
3.126*. Случайный вектор E = (£i»
Ел) прини
мает значения в R k и имеет математическое ожидание
m £ R k и матрицу ковариаций В = ||Ь/у||. Доказать, что:
а) матрица В неотрицательно определена, т. е.
к
2
bijdiCij = (a, Ва) ^ 0 для любого а £ Rk\
i, i = 1
б) если ранг матрицы В равен г, то существует
г-мерная гиперплоскость LrczR k, для которой Р {| £
€ £ г} = 1 , и Р { Е € ^ г - Л < 1 Для любой (г — 1)-мерной
гиперплоскости Lr^1czR k.
3.127. П усть события А 1У Л2, . . . , А п таковы, что
Р {Л 7-} = р, i = l , . . . , n t и событие Вт= {происходит
не менее т из событий Лх, . . . , А п\. Показать, что
¥}
3.128. Случайные величины Е и г] заданы на одном
вероятностном пространстве. Описать множество воз
можных значений Р {Е ^ rj} в следующих случаях:
а) М Е = 1 , Мл = 1 0 ;
б) Е и л одинаково распределены;
70
71.
в) | распределена равномерно на [0, 1], a rj — равномерно на [0, а], а ф 1.
3.129. Случайные величины £ и ц имеют равномер
ное распределение на отрезке [0, 1]. Д оказать, что
при любом характере зависимости между 5 и rj
м ц — r i K 7 23.130. Случайные величины £ и т) независимы и
имеют равномерное распределение на отрезке [0, 1],
а случайная величина £ удовлетворяет условию
P{C = i} = P{C = t i H V . .
Указать совместные распределения £, rj, £, при кото
рых достигаются экстремальные значения М£, и найти
максимальное и минимальное возможные значения М£.
3.131. Случайная величина £ имеет непрерывную
функцию распределения F (х), случайная величина %
принимает только значения 0 и 1: Р{% = 1} = а,
Р{% = 0 } = 1 — а. Указать совместные распределения
£ и %, при которых достигаю тся экстремальные зна
чения М£%, и найти эти экстремальные значения.
3.132. Случайные величины £ и г) независимы и
имеют равномерное распределение на отрезке [0, 1],
а случайная величина £ удовлетворяет условию
Р<£ = £} = / > < 7 2,
Р{£ = т!} = 1 - р .
Указать совместные распределения £, т], £, при к ото
рых достигаются экстремальные значения М£, и найти
эти экстремальные значения.
§ 3. Условные распределения
3.133. Случайные величины £ и г) независимы;
P {£ = fe} = P {n = k) = pqk-\
9 = 1 — р,
0< р< 1,
k = \, 2, . . .
Найти:
а ) Р { 1 = т)};
г) ? { t = k \ t > 4 \е) Р{£ = 6|£ = т,};
з) М{ £ |£ + г, = /},
б) Р {£ > г;};
в )Р {£ < т !};
д) Р {£ = fe| £ < г|};
ж)
P{£ = 6|£ + rj = /};
2.
71
72.
3.134. Случайные величины £, ц независимы и одинаково распределены. Найти условную плотность
PiU +n=z(*) распределения I при условии Е + rj = -г
в следующих случаях: а) £ и т) имеют показательное
распределение с плотностью р (х) = ке-^х, х ^ 0; б) § и г\
равномерно распределены в [0, 1]; в) I и rj имеют
распределение с плотностью Х2хе~%х, х ^ О .
3.135. Найти условную дисперсию D{ £|§ + r] = 2 f
в случаях а), б), в), определенных в предыдущей
задаче.
3.136. Случайные величины
rj независимы и оди
наково распределены. Н ай ти М {| | g + rj = z). Разобрать
отдельно случаи, когда § имеет дискретное распреде
ление или положительную плотность.
3.137. Случайные величины £х, |2,
I n незави
симы и распределены по закону П уассона с парамет
рами Х1Ч
. . . , XN. Найти: a) P{ S1+ . . . + S ft =
= т I ^1+ •••+
=
б) М {§2+ . . .
I§ !+ . . . + I n =
= п\.
3.138. Из урны, содержащей М белых и N — M
черных шаров, сначала извлекается без возвращения
выборка объема п, а затем из этой выборки извлека
ется без возвращения выборка объема п0 < п. Найти
закон распределения числа белых шаров £ во второй
выборке.
3.139. Случайные величины
£2, |3 независимы
и распределены нормально с одинаковыми парамет£ I££
рами а = 0, а = 1 ; положим т] = ^ = И | . Найти плотV 1+ &1
ность распределения г\.
3.140. На отрезок [0, а] брошено три точки, их
координаты
|2, £3 независимы и равномерно рас
пределены на отрезке [0, а]. Найти двумерную функ
цию распределения §2, £3 при условии, что
=
^ m i n { £ 2, £3}, 0 < 2 < а.
3.141. П усть
112), . . . . l n = ( l nl,
—
независимые случайные точки, имеющие равномерное
распределение в квадрате 0 ^ ^ , х 2^ . 1 .
Назовем
точку
=
2) граничной, если для любого
/ = 1, . . . , п выполняется хотя бы одно из условий
|/1 ^
ill*
i/2 ^
i/2*
и обозначим через кп число граничных точек. Найти
М и в.
72
73.
8.142. П усть glf g2, . . . — последовательность независимых одинаково распределенных случайных вели
чин с математическим ожиданием а > 0 и дисперсией
а 2 < оо, случайная величина v не зависит от
£2, ...
и принимает целые положительные значения, Мv = b, а
Т— l l +
“Т ••*
iv
Найти Мт и (при дополнительном условии Dv = 62)Dx.
3.143. Случайная величина § имеет нормальное
распределение с математическим ожиданием 0 и дис
персией а 2. Показать, что при любых х > О, С > О
p {g -* > -£ | E > * }< * -* /«* .
3.144. В схеме Бернулли с вероятностью р исхода
1 и вероятностью q = \ — p исхода 0 найти математи
ческое ожидание числа v00 испытаний до первого по
явления цепочки из двух нулей. В частности, вычис
лить Mv00 при р = г/2.
3.145. В схеме Бернулли предыдущей задачи найти
математическое ожидание числа vln испытаний до пер
вого появления цепочки из трех единиц. В частности,
вычислить это математическое ожидание при р = г/2.
3.146. В схеме Бернулли задачи 3.144 найти мате
матическое ожидание числа v01 испытаний до первого
появления цепочки 01. В частности, вычислить это
математическое ожидание при р = 1/2.
3.147. Точки А и Л2, . . . , А п независимы и имеют
равномерное распределение на окруж ности единичной
длины. Найти вероятность того, что длина наимень
шей дуги, содержащей все эти точки, не больше х ^ 1/2.
3.148. Точки А г, . . . , А п независимы и имеют рав
номерное распределение на окружности S с центром О.
Найти вероятность того, что О лежит внутри выпуклого
многоугольника с вершинами A lf . . . , А п.
3.149. Точки А г, . . . , А п независимы и имеют рав
номерное распределение на окружности с центром О,
а случайная величина v равна наименьшему я, при
котором выпуклый многоугольник с вершинами А 1Э. ..
. . . , А п содержит О. Найти Mv и Dv.
3.150. Точки А 19 . . . , А п независимы и имеют рав
номерное распределение на окруж ности радиуса R.
Найти вероятность того, что выпуклый многоуголь
ник с вершинами A i$ . . . , А п имеет непустое пересе
73
74.
чение с окруж ностью радиуса г = R/2, концентричнойисходной окруж ности.
3.151. Точки Лх, . . . , А п ( п ^ 2 ) независимы и
имеют равномерное распределение на окружности ра
диуса г. П усть Л(Х) = ЛХ, Л(2), Л(з),
Л(и)— точки
Лх, . . . , Л„, расположенные в том порядке, в кото
ром они встречаются при обходе окружности по часо
вой стрелке. Найти закон распределения длины |
дуги Л(1)Л(2) и значения M i, D|.
3.152. П усть выполнены условия задачи 3.151 и
1,-— длина дуги Лш Л(,-+1). Найти совместное распре
деление и коэффициент корреляции i x, |2.
3.153.
П усть выполнены условия задачи 3.152.
Найти закон совместного распределения i x, . . . , i ft
при £ < п.
3.154.
П усть выполнены условия задачи 3.152.
П оказать, что совместное распределение i lV i,v . . . , £t
с 1 ^ ix < i2 < . . . < £ * n совпадает с распределением
! i ...........1к3.155. П усть выполнены условия задачи 3.152 и
v — число дуг А и)А и+1) длины больше Д, 0 ^ Д ^ 2 я л
Найти Mv, Dv и асимптотические формулы для них при
Г= Ш '
3.156.
П усть выполнены условия задачи 3.152.
Найти закон распределения случайной величины
i]„ = m a x {ix, . . . , U .
3.157.
П усть выполнены условия задачи 3.156.
Найти Мг)„ и асимптотическую формулу для Мт]„ при
п —►оо.
3.158. Точки Л, В, С независимы и имеют равно
мерное распределение на окружности единичного ра
диуса. П усть S — площадь Д Д В С , р — его периметр,
г — радиус вписанного круга. Найти MS, M/7, Mr.
3.159. Случайные величины £1э |2, . . . ,
незави
симы,
М§£-= 0,
+ •••+
Показать,
t = 1, 2, . . . , п,
k = l 9 2,
что для любого е > О
M | S ^ | | S ,| > 8 \ > 8 2.
74
п.
75.
3.160.Н е р а в е н с т в о К о л м о г о р о в а . Случай
ные величины i j , |2,
независимы,
М|,. = 0,
D|( = a f < o o ,
i = l, 2,
п,
и S ft=
+ . . . + %k, k = \ , 2, . . . , п. Используя резуль
тат предыдущей задачи, показать, что для любого
е> 0
Р(
\l
max
n
8
f
§ 4. Нормальное распределение
3.161. Случайная величина | имеет нормальное
распределение с математическим ожиданием 0 и дис
персией 1. Какое из двух событий { | 5 | ^ 0 ,7 } или
{ 111 ^ 0,7} имеет большую вероятность?
3.162. Случайная величина £ имеет нормальное рас
пределение с параметрами (0, 1). Что больше:
Р { - 0 , 5 < | < — 0,1}
или
Р{1<|<2}?
3.163. Случайная величина § имеет нормальное
распределение с математическим ожиданием 0 и дис
персией о 2. Найти
f e = l , 2, . . .
3.164. Случайная величина £ имеет нормальное
распределение с математическим ожиданием 0 и дис
персией о 2. Показать, что при любом х > 0
I
V 2л
I*
ж8 /
< - 7L = e " ^ r - .
1
'
К 2л
ж
3.165. Случайная величина § распределена нор
мально с параметрами (а, а 2). Найти:
а) плотность распределения величины r j ^ H 2 при
а = 0;
б) плотность распределения величины г\2 = е% при
произвольных а, а.
3.166. Найти М£ и D§, если 1п£ имеет нормаль
ное распределение с параметрами (а, а 2) (в этом слу
чае говорят, что | имеет логарифмически нормальное
распределение).
3.167. Н екоторая категория людей имеет средний
вес т кг и среднее квадратическое отклонение веса
3 кг. Для случаев т = 60 и т = 10 определить веро
ятность того, что вес случайно взятого человека
отличается от т не более чем на 5 кг, если: а) вес
75
76.
имеет нормальное распределение; б) вес имеет логарифмически нормальное распределение.
3.168. Для случайных величин % ,
определен
ных в 3.166, найти Мт& Mrja.
3.169. Случайная величина | имеет нормальное
распределение с нулевым математическим ожиданием
t
н единичной дисперсией. Найти M §cos| , М i j gа »
М sin|.
3.170. Случайная величина | имеет нормальное
распределение с математическим ожиданием 0 и дис
персией 1. Найти M co s| , D cos§.
3.171. Случайная величина | имеет нормальное
распределение с математическим ожиданием 0 и дис
персией 1. Что больше: Dsi ng или D cos£?
3.172. Случайная величина | имеет нормальное рас
пределение с математическим ожиданием 0 и диспер
сией 1/ 2. Найти M c o s (£ 2), M sin (| 2).
3.173. Случайные величины
|2 независимы и
нормально распределены с параметрами (0, 1). Явля
ются ли независимыми величины Tji = Si + 12» Лг =
3.174.
Случайная величина | нормально распреде
лена с параметрами (0, 1). Положим
g,
— I,
если
если
|1|<1,
| g | > 1.
а) Найти закон распределения rj.
б) Имеет ли величина S + 'П нормальное распреде
ление?
3.175.
Случайные величины Slf £2 независимы и
имеют нормальное распределение с параметрами (0, 1).
Найти
математическое
ожидание
величины
т] =
= е(Sf+6l)/2(1 -f g?-f II)-*/*.
3.176.
Случайные величины S, т] независимы и нор
мально распределены g параметрами (0, а?), (0, а!)
соответственно. Вычислить при о 1 = 1, а 2 = 2 вероят
ность попадания случайной точки (£, rj) £ R 2 в сле
дующие области: а) прямоугольник | * | ^ 1 , | у | ^ 2 ;
б) прямоугольник 0 ^ * < 1 2 , |у |^ 2; в) прямоуголь
ник
2, 0 < у < 4 ; г) трапецию х + у < ; 0, \х\^
1, у ^ — 2; д) область
ограниченную
аллипсом, вписанным в прямоугольник | * | < 1 , \ у \ ^
76
77.
^ 2 ; е) областьх
и
^2 + ^г2^ 1 > ограниченную эллипсом,
описанным около прямоугольника |л:|^1, | у | ^ 2 .
3.177. М ост через реку представляет собой пря
моугольник, координаты к оторого в декартовой си с
теме координат удовлетворяют неравенствам: \ х \ ^ 10,
|у | ^ 1 0 0 . При артиллерийском обстреле моста точка
попадания снаряда (§, г]) в той же системе к оорди
нат имеет двумерное нормальное распределение с неза
висимыми координатами и со средними квадратическими
отклонениями
= 10, ал = 40. «Точкой прицеливания»
назовем (М£, Мг|). Определить вероятность попадания
в мост при одном выстреле, если точка прицеливания
равна: а) (0, 0); б) (10, 0); в) (5, 20).
3.178. Случайные величины £, т] имеют сферически
симметричное нормальное распределение с D§ = Dr) = 4.
Найти вероятность попадания точки (Е, rj) в прямо
угольник с вершинами (0; 3), (4; 0), (1, 8; 5, 4), (5, 8; 2, 4).
3.179. Случайные величины §, г\ имеют двумерное
нормальное сферически симметричное распределение
с М| = Мг] = 0, Dg = Dr] = 1. Найти вероятность попа
дания случайной точки (£, ц) в:
а) треугольник с вершинами (0; 0), (1; 1), (2; 0);
б) треугольник с вершинами (0, 2), (2, 0), (2, 2);
в) треугольник с вершинами (2, 0), (1, 1), (1, 2).
3.180. Случайная точка (£, ц) имеет сферически
симметричное нормальное распределение c D g = Dr)==l.
Найти совместную плотность распределения ее п о
лярных координат.
3.181. Случайная точка (§, г\) имеет сферически
симметричное нормальное распределение с D| = D rj= 1.
Найти вероятность попадания (£, т]):
а) в квадрат С = {(*, у): |х | < 3, |у |< 3 } ;
б) во вписанный в С круг;
в) в описанный около С круг.
3.182. Случайные величины §, rj независимы и нор
мально распределены с M| = M r j = 0, Dg = Drj = 4.
Найти вероятность того, что случайная точка (§, rj)
попадет в:
а) кольцо |(х, у): 2 ^ У х 2 + у2 ^ з } ;
б) область {(я, у): 2 ^ min (|л: |, \у\), тах(|я|, |*/|)^3};
в) область {(*, у): 2 ^ | * | + | у | ^ 3 }.
77
78.
3.183. Случайный вектор 5 = (in £2) € R* имеет двумерное нормальное распределение с нулевым вектором
математических ожиданий, область А — угол с верши
ной в начале координат и раствором а. Д оказать, что
если область А' симметрична области А относительно
начала координат, то Р {£ £ Л '} = Р С А},
3.184. Случайный вектор 1==(|ц |2) С R t имеет не
вырожденное двумерное нормальное распределение
с нулевым вектором математических ожиданий и ма
трицей ковариаций ||а,у |||, ,-=1, |о 1212 < а и а22. Найти
Poo = Р { i l 2=^
?2^ 0 }>
Рю = P { i i < 0 , Ъ > 0 } ,
P o l13 ^ { i l ^
Pu = P { S i < 0 , |2< 0 } .
3.185. Случайные величины
|2, . . . независимы
и имеют нормальное распределение с параметрами
(О, 1). Найти минимальное значение k, при котором
Р {шах {| §! |, |gf |, . . . . | 6 * | } > 2 } > 1 /2 .
3.186. Случайный вектор | = (|1, . . . .
имеет kмерное нормальное распределение с математическим
ожиданием a £ R k и ковариационной матрицей А. Что
больше: M in |6Х. .
l n lM !^ . .$ft|или l n M ^ . . .| А|?
3.187. Случайная величина £ = (Ei, . . . , |„), имею
щая нормальное распределение в R n с нулевым мате
матическим ожиданием и невырожденной матрицей
ковариаций Л=||а^||, не зависит от случайной дей
ствительной величины т], имеющей функцию распреде
ления F (х), Mrj2= l . Найти математическое ожида
ние и матрицу ковариаций случайной величины
=
= 0l£i. •••. л£п)-
Глава 4
ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ.
ПРОИЗВОДЯЩИЕ И ХАРАКТЕРИСТИЧЕСКИЕ ФУНКЦИИ
В курсе математического анализа рассматриваются
различные виды сходимости последовательностей функ
ций: равномерная сходимость, сходимость почти всюду,
сходимость в среднем квадратичном и т. п. По ацалогии
с этим и в теории вероятностей рассм атриваю т^ раз
личные виды сходимости последовательностей случай
ных величин (как функций, заданных на пространстве
78
79.
элементарных событий), а также сходим ость функцийраспределения.
Приведем определения тех видов сходимости после
довательностей случайных величин, которые исполь
зуются в приведенных ниже задачах. П усть на вероят
ностном пространстве (£2, Л у Р) заданы случайные
величины |„ = £w(cd) (со 6 £2» п = 1 , 2, . . . ) и случайная
величина § = £(со), со ££2.
Последовательность glf Н2, . . . сходится к случай
ной величине \ с вероятностью 1 {почти наверное),
если
П оследовательность
£2, . . . сходится к случай
ной величине | по вероятности, если для лю бого е > О
lim Р {|
— 1 1> е} = 0.
Последовательность
?2, . . . сходится к случай
ной величине £ в среднем квадратичном, если
lim M | i„ — £|2 = 0.
Последовательность функций распределения F n(x) =
= Р{ £Л^ х } , п = 1» 2, . . . , слабо сходится к функции
распределения F (х) = Р { К * } , если для любой точки х,
где F (х) непрерывна, выполняется соотношение
lim F n (х) = F (х)
(в этом случае говорят также, что последовательность
случайных величин 11У §2, . . . сходится к § по распре
делению; при этом
Е2, . . . могут быть заданы на
различных вероятностных пространствах).
Все эти определения естественным образом распро
страняются и на случай, когда случайные величины
§2, . . . и | принимают векторные значения.
Понятие сходимости по в е р о я т н о с т и чаще всего
используется, когда предельная случайная величина £
имеет вырожденное распределение (Р {§ = а] = 1 для
некоторого числа а) и
П
79
80.
где£3> ••• — случайные величины (не обязательно
независимые или одинаково распределенные): если
limP { p l:H 7 4:g" - a | > g } - = 0
для лю бого 8 > 0,
(4.1)
то говорят, что последовательность
£а, . . . удовлет
воряет закону больших чисел. Из неравенства Чебышева
нетрудно вывести, что если случайные величины £lf
£2, . . . не коррелированы, М£„ = a, D£„ = а 2 < оо (/г = 1,
2, . . . ) , то (4.1) выполняется; однако закону больших
чисел могут удовлетворять и другие последователь
ности случайных величин (см. задачи § 1).
Если вместо (4.1) выполнено соотношение
Р (со:
lim ^l(co)+ ■” •+ 1п ((й) = а| = 1(
т. е. последовательность
С
4- £
(4.2)
сходится к числу
а с в е р о я т н о с т ь ю 1, то говорят, что последова
тельность
£2, . . . удовлетворяет усиленному закону
больших чисел. Соотношение (4.2) выполняется, напри
мер, если случайные величины
£2, . . . не коррелиро
ваны, М£„ = а, D£„ = а 2 < оо (« = 1, 2, . . . ) , см. задачи
4.20— 4.22.
Пример сходимости п о р а с п р е д е л е н и ю дает
Центральная предельная теорема. Если
£2, . . . —
независимые одинаково распределенные случайные вели
чины, MZ,n = a, D£n = aa < o o (n = l, 2, . . . ) , то для
любого х, — оо < х < оо,
lim
п-+ оо
оуп
у 2п
С e~ ^ d u =
J
= Ф (*).
Сходимость распределений центрированных и нор
мированных сумм случайных величин к стандартному
нормальному распределению имеет место и при других
предположениях о случайных слагаемых (см. задачу
4.124 и другие задачи из § 5).
80
81.
Другим важным примером сходимости по распределению являются теоремы о сходимости к распределе
нию П уассона (см. задачи 4.101 и 4.109).
Практическое значение предельных теорем состои т
в том, что они позволяют аппроксимировать распреде
ления допредельных случайных величин
(при доста
точно больших п) распределением предельной случай
ной величины
это особенно полезно в тех случаях,
когда аналитическая запись функции распределения |
проще выражения для функции распределения
Сле
дует иметь в виду, однако, что вопрос о том, доста
точно ли велико п для то го , чтобы обеспечить нужную
точность приближения, в каждом случае требует о с о
бого исследования; см., например, задачи 2.54, 2.55,
а также 4.103.
Доказательства предельных теорем могут исполь
зовать как прямые вероятностные методы (изучение
распределений допредельных случайных величин или
их моментов, см. задачи из § 2), так и аналитические
методы, основанные на использовании свойств произ
водящих или характеристических функций распределе
ний допредельных случайных величин (см. задачи из
§ 5).
Если случайная величина § принимает только целые
неотрицательные значения, то производящей функцией
распределения Е называется функция комплексного
переменного z
оо
Ф| (z) =
= 2 zh? { ? = £ [ ,
| z | < l;
k= 0
производящую функцию можно рассматривать и в слу
чае, когда S принимает и отрицательные значения,
если область сходимости ряда в правой части послед
него равенства отлична от окруж ности |г| = 1.
Если случайная величина § принимает действитель
ные значения, то характеристической функцией распре
деления | называется функция действительного пере
менного t
ft (t) = Me” 1,
— оо < t < оо;
в частности, если распределение 1 абсолютно непре
рывно и имеет плотность р%(х), то
оо
/§ (* )=
S eitx pl (x)dx.
at
82.
Перечислим важнейшие свойства производящих ихарактеристических функций:
1. Если Р{|Ц < оо} = 1, то
(0) = ф|(1) = 1.
2. Если М |i |ft < оо для некоторого целого k ^ 1, то
dk
h it)
<= о
= ik
<f>i (г)
(по поводу обращения этих утверждений см. задачи
4.65, 4.92).
3.
Если случайные величины
? 2,
%п незави
симы, то
h,+.--+in(t ) = h i ( t ) - ■-hn(t)>
Щг+..-+1п ( 2 ) = Ф 1 , ( 2 ) . . - ф | „ ( 2 )
(обратное утверждение неверно, см. задачу 4.89).
4. Если производящие (или характеристические)
функции распределений случайных величин
и §2 сов
падают, то совпадают и функции распределения
и £2.
5. ( Т е о р е м а н е п р е р ы в н о с т и . ) П оследова
тельность F n (х) = Р
^ х\ ( п = 1, 2, . . . ) функций
распределения слабо сходится к функции распределе
ния F (х) = Р {| ^ . х } тогда и тол ько тогда, когда суще
ствует непрерывная функция
f ( t ) = lim
где
/ „ ( 0 = М е«Ь .
П - * оо
В этом случае f { t ) = Мег/&, и сходим ость f n( t ) —+ f { t )
равномерна на каждом конечном интервале значений t.
обращения.)
6.
(Ф о р м у л ы
Если функция
f ( t ) = tAeu% абсолютно интегрируема, то распределение
случайной величины £ имеет ограниченную непрерыв
ную плотность р (х) и
оо
$ e ~i U f { t ) d t .
~ О
С
Если х и x-\-h — точки непрерывности функции рас
пределения F (х) = Р {1 ^ х\, то
О
О
F ( x + h ) — F (х) _ _ 1
(*
2
■e ~ lth „ - i t
■lim С f (t) е~ aH2l% 1~ г " Н е~ itx dx.
h
2я а 0 J
ltn
7
—00
82
83.
Производящие и характеристические функции векторных случайных величин i = (£i,
!* ) £ /? * опреде
ляются формулами
h ( t » •••> tk) = М exp {*(*& + ... + Ш Ь
Ф1 (2i* •••> zft)= M z | ‘ . . . z f * .
Их свойства аналогичны свойствам производящих и
характеристических функццй одномерных случайных ве
личин. Например, если М | |г». . . | |г* < оо для целых
Гц . . . , гк > 0, то
г1+ . . . + г к
—
TrhVx
h)
= i r1 + . .
d ri + . . . + r k
——
——
д г [ ' . . . д г кк
(zlf . . . , zk)
Z,= . . . = Z b= l -
Таблицы А и Б содержат формулы для производя
щих и характеристических функций наиболее часто
встречающихся распределений.
Отметим, что приведенная в таблице Б формула для
плотности многомерного нормального распределения в R k
имеет смысл лишь в случае, когда матрица ковариаций
В не вырождена (т. е. определитель В отличен от 0).
Если матрица ковариаций случайной величины Б вы
рождена, то (см. задачу 3.126) в R k существует такая
гиперплоскость L, размерность которой равна рангу В,
что Р {£ € £ } = !• Многомерные нормальные распределе
ния в R k с вырожденной матрицей ковариаций В суще
ствуют, но не являются абсолютно непрерывными.
Поэтому при d etB = 0 приведенная в таблице Б фор
мула для плотности неверна, однако формула для харак
теристической функции справедлива.
Многомерные нормальные распределения с вырож
денной матрицей ковариаций естественным образом по
являются как предельные распределения в многомер
ном варианте центральной предельной теоремы: если
£i> £2» •••— независимые одинаково распределенные слу
чайные векторы со значениями в fe-мерном евклидовом
83
84.
ТаблицаА
Производящие функции
Н азвание
расп редел ени я
П р ои зводя щ ая
ф> нкция
Ф орм ула
для Р {£ = /2}
Равномерное
1— Z *
* = 1 . 2 .......... N
Геометрическое
(1 - р ) р к,
1— 2 2
1— Р
1— pz
* = 0, 1, . . .
Биномиальное
* = 0 , 1 ......... п
№
-т т -е -* ,
к\
Пуассоновское
6 = 0,
...
1,
(1 +
P (* -1 ))B
^ (2-1)
Таблица
Б
Характеристические функции
а
1
Равномерное
—,
2а
Показательное
Гамма-распределение
распре
Распределение Коши
—а
х
а е ~ ах ,
'
Г (о)
а
0
’
Х^ °
(х-а )2
202 ’
с
а ] /2 л
— оо < л: < 00
1
Ь
л 62+ * 2 *
— 00 < X < 00
Б " 1 (х - а ))/2
Многомерное
нор
мальное распреде
ление в R k
84
(2я)*/2 Г detB
еш — 1
iat
sin at
at
1
1— i t /а.
1
(!-« )“
69rS
Равномерное
Нормальное
деление
Х а р а ктери сти ческ ая
функция
Ф орм ула
для плотности
а
i
1Q
Н азвани е
расп р едел ен и я
e - b \t\
l a, a) - 4- (t, Bt )
85.
пространстве R k, с математическим ожиданием a £ R k иматрицей ковариаций В (не обязательно невырожденной),
то последовательность распределений случайных величин
Si + . . . + e „ - - t t g
гк
при п — + о о слабо сходится к многомерному нормаль
ному распределению в Rk с нулевым вектором матема
тических ожиданий и матрицей ковариаций В.
§ 1. Закон больших чисел.
Лемма Бореля — Кантелли
4.1. П усть функция g (x ),
неотрицательна
и монотонно возрастает. П оказать, что для любой
действительной случайной величины § справедливо
неравенство
Mg (5)
g(x)
4.2.
П усть случайная величина к\п равна сумме
очков, появившихся при п подбрасываниях симмет
ричной игральной кости. И спользуя неравенство Чебы
шева, оценить сверху
8 > 0.
4.3. П усть £lf i 2, . . . , |„+1 — результаты л + 1
испытаний схемы Бернулли ( Р { § ,= 1} = р, Р
= 0}- =
= 1 —-р) и случайная величина цп равна числу таких
Ч
что Ez. = g/+1 = l . И спользуя неравенство
Чебышева, оценить сверху
8 > 0.
4.4.
Последовательности
§2, . . . и гц, г)2, . . .
образованы одинаково распределенными случайными
величинами, независимыми внутри каждой последова
тельности (случайные величины
и % могут не быть
независимыми), М §2-= Mr]j = a, D£z. = Drjy. < оо. Выпол
няется ли закон больших чисел для последователь
ности £1Э £3, . . . :
— %>k>
Л/г»
^
1э 2,
. . .
85
86.
4.6.Случайные величины
§2, . . . независимы
и имеют стандартное нормальное распределение,
В
ч\п = cos
»
п = 1, 2, . . .
Удовлетворяют ли последовательности г\и г]3, г]5, . . .
и
Чз> •• • закону больших чисел?
4.6.
Последовательность
|2, . . . образована неза
висимыми случайными величинами, имеющими нор
мальные распределения,
= 0,
Dlk = C k«,
С > 0, а > 0 ,
fe = l, 2, . . .
Описать множество тех значений а, при которых после
довательность §!, §2, . . . удовлетворяет закону боль
ших чисел.
4.7. П оследовательность
|2, . . .
образована
независимыми случайными величинами,
М£Л= 0, D^k = Cka ,
С > 0,
а>0,
fe = l, 2, . . .
При каких значениях а последовательность §1? |2, . . .
может удовлетворять закону больших чисел и при
каких значениях а может не удовлетворять ему?
4.8. П оследовательность glf |2, . . . состоит из
независимых одинаково распределенных случайных
величин, М§£ = 0, D ^ = a 2 < o o , f t = l , 2, . . . Удовлет
воряют ли закону больших чисел последовательности
случайных величин
^
Цп
2
ft = 0
^ — 1» 2, . . . ?
4.9. Случайные величины
§2, . . . независимы,
М|, = а, D£(. = <г2 < оо. П усть £„ =
2
£/£/• Пока1< i < / < п
зать, что последовательность
удовлетворяет закону
больших чисел: для каж дого б > О
4.10.
П оказать, что утверждение предыдущей за
дачи останется справедливым, если в ее формулировке
заменить условие независимости
§2, . . . условием
их некоррелированности:
86
87.
4.11.П усть случайный вектор |(Я) = (6Г>» •••» In')
имеет нормальное распределение в R n с нулевым век
тором математических ожиданий и единичной матри
цей ковариаций, а В г>8— множество всех таких точек
* = (*!,
x n) £ R nt что
(1 — в ) г <||x|| = (x f +
. . •+ х п
2 ) 1/2 < ( 1 + Б)г.
Показать, что при любом е > О
П->00
4.12*. П усть случайный вектор %{п) тот же, что
в предыдущей задаче, а С г, 8— множество всех таких
точек х = (х19 . . . , x n) £ R n, что
(1 — в) г
|
|+ . . • + 1
|
(1 + в) г,
в>0.
Показать, что при любом в > О
И ш Р {| “ 6 С „ к 5 5 , | _ 1 .
/2-> 00
Сравнить с результатом задачи 4.11.
4.13. Случайные величины |1( |2, . . . независимы,
одинаково распределены, имеют математическое ож и
дание а и для н екоторого е, 0 < е < 1,
= М | | 1— а|1+8 < оо.
Показать, что для лю бого б > О
lim Р { р 1 + ' п' + 1 п - а | > б | > = 0.
4.14. Л е м м а
Бореля — Кантелли.
П усть
А и Л2, . . . — события, заданные на одном вероятност
ном пространстве, и случайная величина v равна числу
одновременно происходящих событий. Показать, что:
оо
а) если 2 р \ л п} < оо, ТО Р { v < 00 } = 1,
п- 1
б) если события А г, Л2,
оо
И 2
п= 1
...
попарно
независимы
Р { А п\ = 00 > T O P { v = o o } = l .
4.15. П усть А г, Д2, . . . — события, заданные на
одном вероятностном пространстве, и случайная вели
чина v равна числу одновременно происходящих собы
87
88.
тий. П оказать, что если Р { А „ } ^ а > 0, п — 1, 2то
Р {v = оо} ^ а.
4.16. Последовательность чисел сп удовлетворяет
условиям 0 < ! с п^ 1 , Ншс„ = 0. Всегда ли существует
П-+СО
такая последовательность событий А 19 Л2,
что
Р { А п} = с п и для числа v одновременно происходящих
событий справедливо соотношение P { v < o o } = l?
4.17. Последовательность §1? |2, . . . случайных
величин и случайная величина £ удовлетворяют усло
вию
00
2
П—
Р { | — £ |> е} < оо
для лю бого е > 0.
1
П оказать, что Р / lim £п = £\ = 1.
\ п - > 00
/
4.18. Последовательность
|2, . . . случайных
величин и случайная величина £ удовлетворяют усло
вию
2
М ( | „ - 0 2 < оо.
П= 1
Показать, что Р / lim £„ = И = 1 .
00
I
4.19. Случайные величины £lf |2, . . . независимы
и имеют одно и то же показательное распределение
с параметром X:
Р
< х} = 1— е~Кх,
х^О,
/г = 1, 2, . . .
П усть е — произвольное число из интервала (О, 1/Х),
случайная величина v8 равна числу одновременно про
исходящих событий А% = |}|— > у + в|э а (хе — числу
одновременно происходящих событий
BJ = {
max
'У п< k< п
*
а) П оказать, что Р {v 8 < оо} = Р {р8 < оо} = 1 при
любом е £ ( 0 , 1/Х).
б) Вывести из результата п. а), что последова
тельность случайных величин £ „ =
2, . . . , удовлетворяет условию
Е8
ть
max т^ г, п — 1,
к л < n inAJ
89.
4.20.Случайные величины g1# £а# . . . имеют мате
матическое ожидание а и дисперсию а 2 < оо и не коррелир ованы:
М (| ;— а)(£у — а) = 0
при любых i *?*=/.
Д оказать, что
4.21.
Случайные величины
|2, . . . имеют мате
матическое ожидание а и дисперсию а 2 < оо и не коррелированы, а
г)л=
шах
п* < k < (п + I)2
|Hn2+1 + 1«2+2 + . . .
я = 1, 2, . . .
Доказать, что Р J П т
I п _v re ^
= o i = 1.
I
4.22*. У с и л е н н ы й з а к о н б о л ь ш и х ч и с е л .
Доказать, что если случайные величины
|2,
имеют математическое ожидание а, дисперсию а 2 < оо
и не коррелированы, то
§ 2. Прямые методы
предельных теорем
доказательства
В этом параграфе задачи 4.23— 4.33 связаны с на
хождением предельных распределений с помощью ана
лиза свойств допредельных распределений, задачи
4.34— 4.44 — с применениями закона больших чисел,
в задачах 4.45— 4.55 изучаются свойства различных
видов сходимости последовательностей случайных
величин.
4.23. Случайные величины
£2,
независимы
и имеют одно и то же геометрическое распределение
с параметром р , 0 < р < 1:
89
90.
б) Найти# > = lim P { i 1+ . . . + i „ - / n = fe||1+ . . . + l „ > m } ,
m-^oo
k = 0, 1, 2, ...
4.24 (см. задачу 1.40). Первый ряд кинотеатра
состои т из N кресел. Зрители один за другим запол
няют этот ряд, причем каждый из них может с рав
ной вероятностью занять любое из кресел, свободных
в момент его прихода. П усть тх (N ) — порядковый
номер первого зрителя, который сел в кресло, нахо
дящееся рядом с уже занятым креслом, т2 (N) — поряд
ковый номер первого зрителя, который сел в кресло,
симметричное относительно середины ряда одному из
занятых кресел. Найти законы распределения тt (N)
и т2 (N ) и предельные при N — оо распределения сл у
чайных величин Ху - ^ » 1 = 1. 2, т. е. функции Gt (х) =
= lim Р /
^ х\ .
W- оо I
I
4.25. П лотность /?| (х ) случайной величины £ непре
рывна и ограничена на отрезке [а, b] и равна 0 вне
[а, 6]. П оложим
=
где {х } — дробная часть
числа х. Найти
lim
Я-* 00
O ^x^l.
4.26. П оказать, что утверждение предыдущей задачи
справедливо для случайной величины § с кусочно
непрерывной плотностью.
4.27. Случайная величина § имеет непрерывную
плотность распределения р {х ). Найти предельное рас
пределение случайной величины tgn | при п —^ оо.
4.28 (см. задачи 4.26 и 4.27). Случайная величина £
имеет непрерывную плотность распределения р(х).
Найти предельное распределение случайных величин
У __ _ L/ (1
О ~Ь * £ )”
П П ГХ ^
ьп—
_ j _ - j - ( Оi — ij)n при
ti
о ДРР Ь [ __
оо /(здесь
i
у
1 \
).
4.29*. Случайная величина Б имеет нормальное
распределение с математическим ожиданием а и дис
персией а 2. Найти предельное (при я —^ оо) распре
деление для условного распределения случайной вели
чины (£ — х) х при условии I > х. (Ср. с задачей 3.143.)
90
91.
4.30. П усть l i , 12, . . . — независимые одинаковораспределенные случайные величины с функцией рас
пределения F (х), а х„ = ш ах{|1,
Найти такие
последовательности чисел ап и
что последователь
ность апкп-\-Ьп сходится по распределению при п —> оо
к невырожденной случайной величине к, и найти
функцию распределения к в случаях, когда
а )F (x )= 0
-1
( х < 1), F ( x ) = -1 -------- -l
( x > 1, а > 0 ) ,
*
б) F (x ) = m a x {0 , 1—
(* > 0 ),
в) F (x ) = max { 0, 1 — е"*}.
а > 0),
F (х) =
4.31. Последовательности случайных величин |lf
|2, . . . и гц,
г)2, . . . , последовательности действи
тельных чисел
я2, . . . и Ьи Ь2, . . .
при
ц —> оо) и непрерывная функция распределения F (х)
удовлетворяют условиям
lira
оо
lim
n-+cok:
^ x \ = F( x ), — оо < х < со,
I
max
1
1р
|n - k |< Abn I
— 11 = 0 для лю бого Л < оо.
\Пя
j
Показать, что
lim P { r,n~ a'1^ x I = F (x),
«-* oo
I
oo< x <oo.
—
1
4.32. В последовательности
|2, . . . случайная
величина £„ имеет распределение П уассона с пара
метром п:
?{Ъп = к} = ^ е - » ,
k = 0, 1, . . .
Пользуясь теоремой Муавра — Лапласа и результатом
предыдущей задачи, показать, что при любом х,
— оо < х < оо,
х
lim р ] ^ Д < х 1 = Ф ( х ) = ^ L = Г e - u'i*du.
„-*00
\ /л
/
V 2л )
— оо
4.33. Случайные величины §1? Е2, . . . независимы
и имеют одно и то же геометрическое распределение
с параметром V2:
■■■
91
92.
Д оказать, чтоlim Р
п->»
I
У 2п
)
= Ф (дг),
— оо < х < сю.
4.34. П усть |1( 12, . . . и % , г]2, . . . — такие после
довательности случайных величин, что для некоторых
чисел а, b для лю бого е > О
lim Р { Ц „ — а\ > е} = 0,
П-* 00
lim Р { |ri„ — Ь \> е} = 0.
00
Д оказать, что при любом характере
между
и т]„ для л ю бого е > 0:
а) lim Р { Ц „ — а\ < е,
п-> СО
зависимости
|ч\п— b\ < е } = 1;
б) если функция f ( x , у) непрерывна в точке (а, Ь),
то для лю бого е > О
lim Р { I f (Е„. Л„) — f («» Ь) |< e} = 1.
co
4.35. П усть i (‘ ) = ( i i ,) Ы }), i = l, 2, . . . . — незави
симые одинаково распределенные векторы в R 2,
M|i£>= a1 > 0 ,
М|(2£) = а2 > 0,
t = 1, 2, . . .
Д оказать, что последовательность случайных величин
П
—
Ь
S1а>+
+ 6 £Р>
1 + . . . + Й">
Ни — ?а>
S(l) +. 6(2)
й® +, . . . +, £«>
ES »
1
О
П— 1, Z., . . . ,
сходится по распределению к a ^ ,
если
либо
а) Dli” < оо, D||l) < оо, либо б) М |i i ‘ >|1+ £ < оо,
М||^> |1+ Е< оо для некоторого е > 0.
4.36.
П оследовательности
|2, . . . и rjlf rj2, . . .
случайных величин таковы, что
lim Р { |
П-> оо
|^ е} = 1
для лю бого е > О,
и существует функция распределения F (х), для каж
дой точки непрерывности которой выполняется с о о т
ношение
lim Р
лг-> оо
= F (x).
Д оказать, что при любом характере зависимости
между §„ и г]„ для каж дой точки непрерывности F (я)
92
93.
справедливы равенства:а) Jim Р {Л »+ & » < * } = / ’ (х);
б) lim Р{т]п ( ! + § „ ) < 4
я-* со
4.37. В последовательности случайных величин
£i, |2, . . . случайная величина %п при любом п = 1,
2, . . . имеет геометрическое распределение с пара
метром qn, qn - + Q (п —*- оо). Найти предельное р ас
пределение случайных величин
=
при
оо.
4.38. Время | безотказной работы прибора имеет
математическое ожидание а > 0 и дисперсию а 2 < оо.
При каждом отказе прибор подвергается ремонту (и
тогда время до следующего отказа не зависит от
предыстории и распределено так же, как §), после
й-го отказа прибор списывается как негодный. П усть
х * -су м м а р н о е время, которое прибор проработал до
списания.
а) Найти Мт^, Dx^.
б) П оказать, что для лю бого б > О
lim р|
------ 1 > б 1 = 0.
„» I Мт*
I
4.39. П усть
|2, . . . — последовательность неза
висимых одинаково распределенных случайных вели
чин с математическим ожиданием а > 0 и дисперсией
а 2 < о о , случайная величина v не зависит от
£2, ...
и принимает целые положительные значения, Mv = b и
т = ii +§ 2 Ч" •••+ iv
Найти Мт и предельное распределение случайной
величины х/(Мх), когда распределение v изменяется
так, что M v -^ -o o и существует непрерывная функция
распределения
F (х),
удовлетворяющая
условиям
F{0)=0,
l imP
0 <л; <
00.
4.40. Время | безотказной работы прибора имеет
математическое ожидание а > 0 и дисперсию о 2 < оо.
Каждый отказ прибора независимо от предыстории
93
94.
и длин периодов безотказной работы с вероятностью рявляется несущественным (прибор требует только
наладки), а с вероятностью q = l — p — существенным
(прибор нужно ремонтировать). П усть т^ — время от
начала работы прибора до его ремонта.
а) Найти ААт^, Dt^.
б) Найти предельное распределение случайной
величины т^/Мт^, когда параметры а > О и а 2 < оо
фиксированы, a q —>0.
4.41*. На одном вероятностном пространстве
заданы событие Л, Р {Л } = р, и случайная величина §,
имеющая математическое ожидание а и дисперсию
сг2 < оо. Д оказать, что при любом характере зависи
мости между | и Л
Р { I ^ * |Л
р (*—а)® ’
| М {| | Л }-а | < а т т {_ Ц ,
.
4.42*. П оследовательность
гг), (12, е2), , . . с о
стоит из независимых пар случайных величин (внутри
пар случайные величины могут быть зависимыми),
М|г- = a,
Р {в,- = 1} = 1
D i; < a a,
Р {е / = 0 } = ^.
Положим v = m i n { i ^ l : ez- = 1
Ti = §i + . . . + 5 v - i
(Xi = 0 при v = 1),
T2 = ^1 + •••+ 5v
Найти предельные распределения случайных величин
qTlt qT2y когда параметры a > 0 и a 2 < оо фиксиро
ваны, а q —>0.
4.43.
П роцесс работы прибора состои т из незави
симых одинаково распределенных циклов; длина g
цикла имеет математическое ожидание а > 0 и дис
персию а 2 < оо. Вероятность того, что за один цикл
прибор не сломается, равна /?, вероятность поломки
прибора на любом фиксированном цикле равна q — 1—р
(поломка прибора может зависеть от длины цикла).
П усть т — время до первой поломки прибора.
Найти предельное распределение случайной вели
чины q%/a, когда q —>0, a —* a 0 > 0, a 2—> a ;J < oo.
94
95.
4.44. В бункер помещается не более N = 150 деталей. Ежеминутно в бункер поступает случайное число
деталей, имеющее распределение Пуассона с пара
метром Х=2\ числа деталей, поступающих в бункер
в непересекающиеся интервалы времени, независимы.
Через каждый час все находящиеся в бункере детали
перегружаются в тележку и отправляются на дальней
шую обработку. В начальный момент времени бункер
свободен. Пользуясь предельными теоремами, указать
приближенное значение вероятности того, что за время
Т = 100 часов не произойдет ни одного переполнения
бункера.
4.45. П оказать, что если последовательность слу
чайных величин
|2, . . . сходится к £ с вероят
ностью 1 или в среднем квадратичном, то она с х о
дится по вероятности и по распределению. Привести
пример последовательности
|2, . . . , сходящейся
к | по вероятности, но не сходящейся ни в среднем
квадратичном, ни с вероятностью 1.
4.46. П оследовательность случайных величин
Н2, . . . , сходится к £ по распределению. П оказать, что
можно задать на одном вероятностном пространстве
случайные величины
|2> ••• и
так, что для всех х
P {tn < x \ = P {tn < x\ ,
п = 1, 2, . . . ,
и последовательность
£2, . . . сходится к
с веро
ятностью 1.
4.47. П усть f (х) — непрерывная функция, х £ (— оо,
о о ), а последовательность случайных величин
|2, . . .
сходится к случайной величине £ (с вероятностью 1,
по вероятности или по распределению).
а) Сходится ли (в тех же смыслах) последовательность f i h ) , f ( l 2), . . . к /(£ )?
б) Сходится ли (в тех же смыслах) последова
тельность / ( £i ) , / ( £ 2)>
к f(| ), если f ( x ) к усочн о
непрерывна (имеет конечное число разрывов на любом
конечном интервале), а функция распределения §
непрерывна?
4.48. П оследовательность
£2, . . . случайных
величин удовлетворяет условиям
р {Би+1 > £ я} = 1 Для любого п = 1 , 2, . . . ,
lim N\£n = a < о о .
95
96.
Д оказать, что сущ ествует случайная величинакоторой
для
Верно ли равенство М ! = а?
4.49. П оследовательность точек |х, 5а* ••• на
отрезке [0, 1] строится по следующему правилу: gx
имеет равномерное распределение на [0, 1], и если
значения gx,
определены, то точка gft
имеет равномерное распределение на минимальном по
длине из k отрезков, на которые [0, 1] разбивается
точками gx, . . . . gft_ x.
а)
Д оказать, что существует случайная величина |,
удовлетворяющая условию P{lim g„ = g} = l.
б) Найти М|, Dg.
4.50.
П оследовательность точек g0, gx, g2, . . . на
отрезке [0, 1] строится по следующему правилу: g0 =
= 0, gx имеет равномерное распределение на [0, 1], а
g„ при любом « > 2 имеет равномерное распределение
на интервале, образованном g „_ x и g „_ 2.
а)
Доказать, что существует случайная величина g,
удовлетворяющая условию Р {lim g rt = g} = 1.
б) Найти Mg, Dg.
4.51*. Функция распределения F (х), последова
тельность случайных величин gx, g2, . . . и последова
тельность чисел ап, Ъп удовлетворяют условиям
в каждой точке непрерывности F (х),
lim F (х) = 0,
Х-+—
lim F (х) = 1;
СО
последовательность функций g „ ( x )
п = 1, 2, . . . ) такова, что если
( — oo<jc<oo,
18п К + У)— ёп M — ygn (ап) I,
то П тг 1У „(Л ) = 0
96
для лю бого А < оо. Найти
97.
4.52.Функция распределения F (х), последователь
ность случайных величин
£2, . . . и последователь
ности чисел ап, Ьп удовлетворяют условиям
lim p l h i ^ a n
П-+ <*
\
=
I
°п
в каждой точке непрерывности F (х),
lim F (x ) = 0,
—
00
l i m / :'(x ) = l;
X- > со
последовательность функций g n (x) ( — оо < х < оо,
п = 1, 2, . . . ) такова, что если g „(k>(ап) Ф 0 и при неко
тором натуральном k
wn (Л )=
sup
А тгг , I gn (an + y ) — g„ (ап)— yj g (nk,(an)
IУ\<АЬп\ У \ gn ( а п) I
то lim wn ( A ) = 0 для любого A < оо. Найти
lim P f
11111 Г <
(?n)
g n (fl«)
bngn
\ a n)
LTjk)
.K XtZ) / Л \
<X]
4.53.
Последовательность случайных величин £lf
|2, . . . и последовательности чисел alt a2, . . . и 61э
b2, . . . удовлетворяют условию
lim Р<
Я-> сю
I
-
< х > = Ф ( х ) для любого х,
°п
)
|х| < ОО.
Пусть а'и а2, . . . и
Ь2, . . . — две другие последо
вательности чисел. Рассмотрим три группы условий:
а) lim
л -*ао
= lira | s = l ,
a «
Я —>-оо
б) lim ( a ;— a„) = lim (b’n — bn) = 0,
Я->00
я->оо
в) lim — ~ gn = Q,
lim -^ = 1.
Какие из условий а), б), в) обеспечивают выполнение
соотношения
lim p j ^ ^
Я-> С
Ю ' Ьп
< х ! = = Ф ( х ) для любого х,
'
|х|<оо?
97
98.
4.54. Последовательность случайных величин 51#£2,
. . . сходится к случайной величине £ по распре
делению.
а) Пусть существуют и конечны величины
m = М£,
тп =
тоо = lim m„.
ti-+co
Какие из соотношений т < т^, т = тж, m >
могут,
а какие не могут выполняться?
б) Ответить на вопрос п. а) при дополнительном
условии М|2 < оо, lim М£2 < оо.
ГС-*00
4.55. Последовательность случайных величин
g2, . . . сходится к случайной
величине § по распре
делению.
а) Пусть существуют и конечны величины
М = Mg*,
М п = М|2,
М ж= lim М „.
гс-* со
Какие из соотношений 7W < М^, М = М т, М > М т
могут, а какие не могут выполняться?
б) П усть существуют и конечны величины
o 2 = Dg,
<£ = DgB,
at, = lim a2.
rc-> со
Какие из соотношений a2 < a t , a 2 = a i , а 2 > а ! могут,
а какие не могут выполняться?
§ 3. Характеристические и производящие функции
В этом параграфе задачи 4.56— 4.70 связаны с вычис
лением производящих функций и моментов случайных
величин, задачи 4.71— 4.81 — с вычислением характе
ристических функций, в задачах 4.82— 4.95 рассматри
ваются различные свойства характеристических функ
ций, а в задачах 4.96— 4.100 вычисляются характе
ристические функции специальных распределений и
исследуются свойства многомерного нормального рас
пределения.
4.56.
Найти производящие функции целочисленных
распределений:
yji
а)
п уассон овск ого: Р = k)
k = 0, 1,
2, . . . ; 0 < А, < оо;
98
99.
б) геометрического: Р{| = 6} = /?<7*, 6 = 0, 1, 2,р, q > о, p + q = i;
в) биномиального: Р {%= k} = CnPkqn~k, £ = 0, 1» . . .
n; р, q > 0, p + q = 1.
4.57. Найти производящ ую функцию ф (г) числа \п
успехов в п независимых испытаниях, если вероят
ность успеха в каждом испытании равна р. И споль
зуя этот результат, найти формулы для Мi„ , M ijr 1
( 6 = 1 , 2, . . . ) , D%n.
4.58. Производящая функция распределения сл у
чайной величины Е, принимающей целые неотрица
тельные значения, равна ср(г) = Мг?.
а) Найти M l, D i, M ( i - M i ) 3.
б) Найти производящие функции величин i/2 ,
2 i, — i и случайной величины i x— i a, где i x и i 2—
независимые случайные величины, имеющие то же
распределение, что i.
в) Д оказать, что при b > а > 0
1
M iq r j =
(z) dz,
о
1
г
М (|+с)(| + б) = I гь~а~1 J и“ -1Ф («)
о
о
4.59. Пусть Ti — порядковый номер первого из ис
пытаний схемы Бернулли (т. е. последовательности
независимых испытаний), которое окончилось успе
хом (вероятность успеха в каждом испытании равна р ,
неудачи — q = 1 — р ). Найти Mxlf D t1? М гЧ
4.60. В схеме Бернулли обозначим через
п о
рядковый номер испытания, в котором появился &-й
успех; считая вероятность успеха в каждом испыта
нии равной р, найти:
1) М0*, D0ft;
2) фей( г ) = М г 0*.
4.61. Закон распределения случайной величины %
определяется формулой
P { i — n} = C ^ p mq " - m,
п —т ,т + \ ,
99
100.
где m — целое положительное число, 0 < / ? < 1 , q == 1 — р. Найти производящ ую функцию распределе
ния £ и ME, D|. П оказать, что распределение | с о
впадает с распределением суммы т независимых оди
наково распределенных случайных величин.
4.62. Найти закон распределения г| = Е1+ Н2+ ^3,
если у |2, Е3 независимы и при
1, 2, 3; 0 < р < 1,
< 7 = 1 - /? :
4.63. Случайная величина v распределена по за
кону П уассона с параметром К и не зависит от ре
зультатов испытаний схемы Бернулли с вероятностью
успеха р. Обозначим jjlv число успехов в первых v
испытаниях схемы Бернулли. Найти:
а) 9uv (г) = М г Ч
б ) M p v, D|JIV.
4.64. Производящая функция совместного распре
деления величин У Е2 равна
Ф^1 ^2 (^) ~ ^ ^ lZl +^22г+ Гз2122” !) ,
где р 1 + р2+ Рз = 1>
0, 1= 1, 2, 3. Найти:
а) одномерные распределения ^ и У
б) М У М£2, D y D|2, c o v (6 lf У .
Являются ли величины
и
независимыми?
4.65. Целочисленная неотрицательная с вероят
ностью 1 случайная величина I имеет производящую
функцию ф^(г). Д оказать, что если для целого k ^ l
lim -^—г ф& ( 2)
и 1 1 dz k
= mk < оо,
z —u
ТО
=
— l ) . . . ( g - f e + l)=m*.
4.66.
Пусть у t — число появлений г-го исхода
в п независимых испытаниях с N несовместными
исходами и вероятностью pj появления /-го исхода
в каждом испытании ( / = 1, . . . , N). Найти
а) ф ( г г
б) М&*1,, М
100
=
(
г
Ф /; ft, / = 1, 2, . . . ).
101.
4.67. П усть выполнены условия предыдущей задачи и N = 4,
Л/г, X
^/г, 1» Л/г. 2 ^/г. 2 ^/г. 3>
Л/г, 3 ~ ^>/г, 4»
£/г, г = £/г, f + ^/г, г+1
(1 = 1. 2, 3).
Найти производящие функции распределений векто
ров (Ия, X I л /г, 2> Л/ г, з)> ( С / г , X » С/г, 2> С и , з) И КОЭффИциенты корреляции р (rj„. х, г\„, 2), р (£ „ .!,
2).
4.68. П усть величина v имеет распределение П уас
сона с параметром X и не зависит от исходов испы
таний полиномиальной схемы, описанной в задаче 4.66.
Найти производящую функцию распределения слу
чайного вектора (£v> lf . . . , |v. дО4.69. При каких значениях параметров дробно
линейная функция у (г) =
^
будет
производящей
функцией целочисленной случайной величины?
4.70. Производящая функция распределения сл у
чайной величины 5, принимающей целые неотрица
тельные значения, равна y ( 2 ) = Mz*. Выяснить, при
каких условиях следующие выражения являются про
изводящими функциями вероятностных распределений,
и если являются, то указать, как соответствующ ие
распределения связаны с распределением
ф ( г ) = Ф'<г> .Ф х^
ф' (1 —)
/ \
Фз (*) “
1— а
1—аф
»
ф (г\= ___ !___ ^ Ф Е ).
ф' (1 —) 1— г ’
, ч
Ф4 (г ) ~
ln©(z) . «
in ф (0) “Ь »
Фз (2) = Кфз (г) .
4.71. Производящая функция целочисленной слу
чайной величины I равна ф§(г). Найти характеристи
ческую функцию
4.72. Найти характеристические функции распре
делений:
а) п уассон овского: Р
= т\ = - ^ - е ~ х, т = 0, 1 , . . . ;
б) биномиального:
Р { t = m\ = C^pmqn~m,
1» •••»
в) показательного: р^(х) = а£~ах, * > 0 .
m=s 0,
4.73. Случайные величины
g2, . . . независимы
и имеют показательное распределение с параметром ос:
Р
*> 0 ,
f = l, 2, . . .
101
102.
Найти М ( ? ! + . . . + 1 Л)А при любых значениях k t п =я= 1, 2, . . .
4.74. Случайные величины
|2, . . . независимы,
одинаково распределены и имеют характеристическую
функцию f (t) =
(производящую функцию cp(s)=:
= M s^), случайная величина v не зависит от
g2, . . . ,
принимает только целые неотрицательные значения
и имеет производящую функцию g (s ) = Msv. Найти
характеристическую функцию (производящую функ
цию) случайной величины
( Si + ?2 + ••* + £v
\
0
ПРИ
при
v = 0.
4.75.
Случайная величина §имеет
биномиальное
распределение с параметрами (п , р), т. е.
Р {5 = Л} = С * / > * ( 1 Л = 0. 1,
п.
При каких условиях можно представить £ в виде
Е = Ei + Ег Н~ •••Н~ Ет>
где §lf
независимы и при любом t = l ,
т
случайная величина £,• имеет биномиальное распре
деление с параметрами (nh р{) (n ,-^ 1, 0 < р { < 1)?
4.76. Случайная величина | принимает только це
лые значения, и f ( t) = ЬЛеи%— характеристическая функ
ция распределения
Найти:
а) Р{| = 0 (m od k)};
б) Р {1 = tn (mod k)\.
4.77. Независимые случайные величины |х, |2, . . .
имеют равномерное распределение на множестве {1,
2, . . . , 3k). Найти
maxP{g? + . . . + 1 ^ 0 (mod 3)},
minP { i i + • ••- f IS =5 0 (mod 3)}.
П> 1
4.78. Случайные величины £1Э £2, . . . ,
незави
симы. Д оказать, что для лю бого действительного Я,
удовлетворяющего условиям
<
102
оо,
i = 1, . . . ,
я,
103.
справедливо равенство1=1
4.79. Случайная величина 5 принимает действи
тельные значения. Доказать, что для любого действи
тельного х
Р
inf е-**МеМ9
%> о
^ х\ ^ inf e KxtA e -%^.
к>0
4.80. П усть \in обозначает число успехов в п не
зависимых испытаниях с вероятностью р успеха в каж
дом испытании. Д оказать, что при а < р
рк«».|«{(45ГЭТ
Найти аналогичную оценку для Р{|хп ^ $ п \ при Р > р
и для Р { р „ < п / 2 } при р > х/2.
4.81. П усть р„ — число успехов в п независимых
испытаниях с вероятностью р успеха в каждом испы
тании. Положим Ti„ = max {р„, п — p„}. Д оказать, что
при п - i-oo, р > q = 1 — р
МцОТ = MjiM + О (n*P»)f
где Р = 2
pq < 1 . Найти lim — Dti„.
П-* оо n
4.82. Случайные величины i lt |2 и и независимы,
характеристические функции
и £2 равны
(t) и
f2(t) соответственно, Р {х = 1} = 1 — Р{ х = 0} — р(~ (0, 1).
Найти характеристическую функцию случайной ве
личины
ti = x ii + ( l — х) i 2
(распределение т] называется смесью распределений
h и 5,).
4.83. Показать, что если Р { | Ц < о о } = 1, то функ
ция f ( t ) = ЬАе1% — оо < ^ < оо, равномерно непре
рывна.
4.84. Характеристическая функция f { t ) =
при
нимает только действительные значения. Доказать,
что при любом действительном t
=
t),
{03
104.
4.86. Найти характеристическую функцию:а) равномерного распределения на отрезке [0, а];
б) «треугольного» распределения с плотностью
J а ( 1 — ос|л:|)
Ра(х ) — I Q
при
П р И
| х | ^ а ~ ь,
|х j
ос 1;
в) распределения с плотностью
<?«(*) = ^ Г ( l — c ° S - j ) .
— ОО < х < оо.
В случае в) найти значение Са, при котором qa (x)
оказывается плотностью вероятности.
4.86. Функция f ( t ) t — o o < f < o o , обладает сле
дующими свойствами:
а) f ( 0) = 1, f ( t ) ^ 0 для лю бого t\
б) f { t ) = f ( — t) для любого t\
в) графиком f ( t ), 0 ^ / < о о , является выпуклая
вниз ломаная линия, состоящ ая из конечного числа
звеньев.
Является ли f (t) характеристической функцией
распределения вероятностей?
4.87. Функция f (t), — оо < t < оо, обладает сле
дующими свойствами: / (0) = 1, f ( t ) ^ 0 , f (t) — f (— t)
для лю бого t , f ( t ) непрерывна и f " ( t ) ^ 0 для лю
б ого t =т^=0. Является ли f ( t ) характеристической функ
цией распределения вероятностей?
4.88. П усть а > 0 и функция
(t) имеет период 4а,
fl (0 = l - 4 L -
Н К 2*-
а) Является
характеристической функцией?
б) Является ли характеристической функцией функ-
ЦИЯ / 2( 0 = l f i ( 0 l ?
4.89. Случайные величины i j, . . . , %к (k > 1) неза
висимы и имеют функцию распределения F (х), слу
чайные величины Tjlt
независимы и имеют функ
цию распределения G {x). Следует ли из условия
Р
+ •••+ ift < х\ = Р К + . . . + Tift < х} для
каждого х
совпадение функций распределения F (х) и G (x)?
4.90. Изменится ли ответ на вопрос предыдущей
задачи, если дополнительно
потребовать,
чтобы
104
105.
P \\%i+ •••+1*1 < ° ° } = 1 и характеристическая функция распределения ^ нигде не обращалась в нуль?
4.91.
Показать, что если характеристическая функ
ция f ( t ) = t A e u^ удовлетворяет условиям
/ ( <0 = /( * .) = !.
то при любых целых т, п — 0, ± 1 , ± 2 , . . .
f (mt1+ nt2) — 1.
4.92*. Характеристическая функция f ( t ) — tAeu^
дифференцируема при t = 0. Верно ли равенство
м |= |п о )?
Рассмотреть случай, когда § имеет плотность рас
пределения р{х), причем
р ( х ) = р ( — х),
p ( x ) = ~"zr f c l )-
(Х — оо).
4.93*. Характеристическая функция f ( t ) = Ме‘7£
удовлетворяет условию | Г ( 0 ) | < о о . П оказать, что
М|2 < |f" (0) |< оо.
4.94. Показать, что если характеристическая функ
ция / (t) = М е'^ дважды дифференцируема при t = 0
и |/ " (0) |< оо, то I f ' (01 < Г"|Г(0)| ПРИ любом t.
4.95. Являются ли характеристическими функциями
вероятностных распределений следующие функции:
а)
д) |cos ^ |2/3;
б) cos (f*);
е)
в) cos2 <;
ж)
г) cos(| 112/ 3);
з) е-1 * I?
1 (< = 0);
е~2< ( ^ 0 ) ;
(^ < 0 );
4.96. Случайные величины
£2, . . . независимы
и имеют одно и то же нормальное распределение
с параметрами (0, 1). Распределение случайной ве
личины
х»-й+а+...+»
называют %2-распределением с т степенями свободы.
105
106.
а) Найти функцию распределения и характеристическую функцию ^-распределения с двумя степенями
свободы.
б) Найти характеристическую функцию и формулы
для моментов А-го (& = 1, 2, . . . ) порядка ^ “распре
деления с г степенями свободы.
4.97. И сходя из формулы для плотности гаммараспределения (см. введения к гл. 3 и 4), проверить,
что если случайные величины
и |2 независимы,
имеет гамма-распределение с параметром a, a 12 —
гамма-распределение с параметром |3, то h +
имеет
гамма-распределение с параметром а + р. Используя
это свойство семейства гамма-распределений, найти
характеристическую функцию f a (t) и формулы для
моментов т$ (k = l, 2 , . . . ) fe-ro порядка гамма-распре
деления с параметром а > 0.
4.98. Случайный вектор (§lt . . . ,
имеет много
мерное нормальное распределение в R k с вектором
математических ожиданий а = (а1У . . . , ak) и матрицей
ковариаций В . Найти распределение случайной вели
чины
£ = ci§i + •••+ сЛь
где с1ч . . . , ck— действительные числа.
4.99. Случайный вектор
. . . , %k) имеет много
мерное нормальное распределение в R k с вектором
математических ожиданий a = (alf . . . , ak) и матрицей
ковариаций В\ матрица С=||с,7 || (i = l, . . . , т\ j =
= 1, . . . , k) состои т из действительных чисел. Найти
распределение случайного вектора (gj, . . . , £от), где
Si =
~Ь ••
1 = 1, •••»
4.100. Случайный вектор | =
. . . , £й) имеет
многомерное нормальное распределение в R k с векто
ром математических ожиданий а = (а1, . . . , ak) и не
вырожденной матрицей ковариаций В. Показать, что
сущ ествует такое ортогональное преобразование С
пространства R k в себя, что вектор 'П= (г)1, . . . , rjfe) =
= С\ имеет многомерное нормальное распределение с
независимыми компонентами.
*06
107.
§ 4. Неравенства Бонферронии сходимость к распределению Пуассона
4.101. Случайные величины 1[п\ Ц ” , . . . , |^'г) неза
висимы,
Р {1/г'г) = 1} = 1— Р {lfen) = 0} = рк (п),
k = l,
2,
...,
п.
П усть при п —*■оо
1
шах рк(п ) ~ * 0,
р1 ( п ) + . . . - \ г р п (п )~ ^ К , 0 < Х < о о .
П
<
Используя метод производящих функций, найти
lim Р { E f > + . . . + i r = m } ,
m = 0, 1 , . . .
П —► оо
4.102. Случайная величина | принимает значения
1 и 0 с вероятностями р и <7 = 1— р соответственно,
а случайная величина rj имеет распределение П уассона
tyk
с параметром р: Р {rj = k\
k = 0, 1 , 2 , . . . Д ока
зать, что | и rj можно задать на одном вероятност
ном пространстве так, что P {g ^ = rj} < р 2.
4.103. Случайные величины
§2, . . . , \п незави
симы, Р{Н< = 1} = 1 — Р{§; = 0} = Pi, i = 1, . . . , п. И споль
зуя результаты задачи 4.102, доказать, что
~9~ Yh j р { i i + • • • + ? « = Щ—
k= 0
- g - ( P t + . . .+ Р и ) I ^
*
1=1
4.104. П усть А 19 А 2, . . . , A n — совокуп н ость с о
бытий и событие Вг состои т в том, что одновременно
происходит ровно г из событий А 19 . . . , A n . Д ока
зать, что при любом r = 0, 1, . . . , N
р w = 2 ( - i ) ft- ra s * ,
к-г
где S 0 = l, Sk =
2
P { A i Ai . . . A i A .
4.105*. Случайная величина § принимает только
целые неотрицательные значения. Д оказать, что если
107
108.
т * = М Е Ю - = М Е ( 6 - 1 ) . . . ( 5 - Л + 1 ) , 6 = 1, 2, . . . . и дляцелого d ^ l величина т 2^-х < °°» Т0
2d
2d —I
Е ( - 1 ) * - 1т г < р <Е > ° к
/г=1
4.106. П усть
Д оказать, что
выполнены
Е
/г= 1
(—
условия
n+2d-l
n + 2d
k=n
k-n
если n = 0, 1, . . . и m „+2d_x < оо.
4.107. П усть выполнены условия
Д оказать, что при любом п = 1, 2, . . .
n+2d-l
n+2d
k —n
k —П
задачи
4.105.
задачи
4.105.
если mn+2d_ l < oo.
4.108. М е т о д м о м е н т о в . П у с т ь ^ , §2, . . . — по
следовательность
неотрицательных
целочисленных
случайных величин и
т р = М ^*1
(п , 6 = 1, 2, . . . ) .
Д оказать, что если существует такая целочисленная
неотрицательная случайная величина
что при любом
k = U 2, . . .
lim raj^ =
< оо
П — oo
и mft = o ( 6 ! 6 - r ), 6 —s-oo, для лю бого г < oo, то
lim P
П-+00
= 6} = P {§ = 6},
6 = 0, 1, 2, . . .
4.109. П усть lx, £2, . . . — последовательность не
отрицательных целочисленных случайных величин.
Д оказать, что если при любом 6 = 1 , 2 , . . .
lim
= Хк,
0 < А. < оо,
П-^оо
то
lim Р {£„ = т } = Ц -е -х для лю бого т = 0, 1, 2, . . . ,
Я->°о
т. е. распределение %п сходится к распределению П у
ассона с параметром К при п —>оо.
108
109.
4.110. Пассажирский поезд состои т из N вагоновпо s мест в каждом вагоне. В момент отправления
в поезде находилось п пассажиров. Обозначим сим
волом |Л/= [Jt£*(/г, /V, s) число вагонов, в которых при
отправлении поезда находилось ровно i пассажиров,
t = 0, 1, . . . , s. Предполагая, что все n\C%s= (N s)W
вариантов размещения пассажиров в поезде равнове
роятны, найти формулы для факториальных моментов
величин (х0, (jij, . . . , \is. Проанализировать поведение
математических ожиданий |л/ при изменении п от 0
до Ns.
4.111. Пусть выполнены условия задачи 4.110.
Найти явное выражение для P{jjtf.(n , N, s) = k}.
4.112. П усть выполнены условия задачи 4.110.
П оказать, что если s и i фиксированы, а п, N —> оо
так, что
N, s ) —
0, оо), то при любом
k = \ y 2, . . .
(Пу Ny
—> №.
Вывести отсю да, что тогда для любого т = 0, 1, . . .
p{ f i , ( n, N, s) = m} — ^ e - \
4.113. П усть п частиц размещаются по N ячейкам,
причем каждая частица независимо от остальных с
одинаковыми вероятностями (равными 1/N) может
попасть в любую из N ячеек. Обозначим через jxr (n, N)
число ячеек, в которых находится ровно по г частиц.
Найти формулу для Mjjir (n, N) и доказать, что если
r = 0, 1, 2, . . . фиксировано, a п, N —> оо так, что
Mjir (Пу N ) —+ k , 0 < X < оо, то
Р { М « . N) = m\
m = 0, 1, . . .
4.114. П усть частицы последовательно и независимо
друг от друга размещаются по N ячейкам так, что
i -я ( i = 1, 2, . . . ) частица попадает в /- ю (/ = 1, . . . , N)
ячейку с вероятностью 1/N. Положим
vr (N) = min {п: \ir (п , N ) > 0},
г= 2,3,...,
где [хг (Пу N) — число ячеек, содержащих после разме
щения п частиц ровно по г частиц. Найти такую по
следовательность чисел ЬХу Ъ2у . . . , что распределения
случайных величин vr (N)/bN при N - + оо и фиксиро
109
110.
ванном г сходятся к невырожденному закону, и сампредельный закон.
4.115.
П усть п частиц назависимо размещаются
по N 2 ячейкам, расположенным в виде квадратной таб
лицы размером N x N . Назовем ячейку свободной , если
после размещения п частиц ни в нее, ни в ячейки,
находящиеся с ней в одной строке или в одном столбце,
не попало ни одной частицы. Найти предельное рас
пределение числа к (п , N) свободных ячеек, когда
n = N (In XN + о (1)),
N —^ оо.
§ 5. Применения центральной предельной теоремы
и метода характеристических функций
4.116 (см. 4.2). Случайная величина цп равна сумме
очков, выпавших при п независимых подбрасываниях
симметричной игральной кости. Используя централь
ную предельную теорему, выбрать п так, чтобы
4.117. Складывается 104 чисел, округленных с точ
ностью до 10~т. П редполагая, что ошибки округления
независимы и равномерно распределены в интервале
(— 0,5*10-/Л, 0 ,5 -1 0 ""2), найти пределы, в которых с
вероятностью, не меньшей 0,99, будет лежать сум
марная ошибка.
4.118. Случайные величины g1# g2, . . . независимы
и имеют стандартное нормальное распределение. Р ас
пределение случайной величины
Хп = £ ! + • • • +
называется распределением %2 (хи-квадрат) с п степе
нями свободы .
а) Д оказать, что lim Р j I
— 1 1> e l = 0 при любом
П-+оо
II™
I
/
8 > 0.
б) Найти
lim Р ( У-п-~ - ^ п-
я-*-”
, — оо < х < оо.
У DХп
’
4.119. Случайные величины £0, £х, |2, . . . незави
симы и имеют стандартное нормальное распределение.
110
'
111.
Распределение случайной величинытц= ——
.
h
V&1+...+12
п)/п
называется распределением Стьюдента с п степенями
свободы. Найти
lim Р {т„
х},
— оо < х < оо.
оо
4.120. П усть
обозначает число появлений г-го
исхода в п независимых испытаниях с N несовмест
ными исходами; вероятности появления этих исходов
в каждом из испытаний равны р1# р 2,
рд г^ О
соответственно, рг + . . . -\-pN = 1. Далее, пусть alt . . . ,
aN— действительные числа и
,/Пп = а15»,1+ ••
Найти Mr)n, Dr)rt и предельное распределение -11п~~Мг]д
V DT|„
при п
оо.
4.121. Случайные величины l lt g2, . . . независимы
и одинаково распределены; М%k = a, Dlk — b2, k = l 9
2, . . . Положим
лЛ= £Л+ £*+1 + £*+2, * = 1 , 2, . . .
Найти:
а) Мт|* c o v ( % , т]/)
’
л -> «
\
b V ln
Ог\к\
/
4.122. Случайная величина ix распределена по за
кону П уассона с параметром Я. Найти
lim p {-^ i< 4 .
w - I VT.
>
4.123. Два игрока заняты азартной игрой, состоя
щей в подбрасывании несимметричной монеты, которая
падает «гербом» с вероятностью р > 0 и «решкой» с
вероятностью q =?= 1 — р > 0. Ставки игроков в каждом
туре равны соответственно ^ > 0 и а2 > О руб.; если
монета падает «гербом», то выигрыш ^ + а2 получает
первый игрок, если «решкой» — то второй. Предполо
жим, что исходные капиталы игроков бесконечны, и
обозначим через Sfr* суммарный выигрыш первого иг
рока за п туров, а через
S^2) ( = — SJP) — в тор ого.
Показать, что:
ш
112.
а) существует только одно такое значение х > О,что при aja.2 = x для лю бого у , | у | < о о ,
lim Р {S p > у } < 1
и
lim Р
П—
> ОО
>(/}<!
п-*~ оо
б) если аг = а2х, где значение х то же, что в п. а),
то
lim Р {S<« > S?\ = lim Р {S%> < S«>} = \ .
П-4-оо
П-> oo
4.124. П оследовательность случайных величин %19
§2, . . . такова, что при любом я = 1, 2, . . .
:= £ h ,1 +
£ h, 2 +
• • • + £ n ,n *
где £rtjl, . . . , ^ „ — независимые случайные величины,
М£й>/ = 0,
Л
^ = Е°Ся.*<«>.
£=1
* = 1, . . . , я,
п
Н т - Ь Ц M|C„tft|3= 0.
«-^00 S'* fc=l
Доказать, что распределения случайных величин £„/sn
при я —> оо сходятся к стандартному нормальному
распределению.
4.125. Случайные величины
§а> ••• независимы,
Р {| „= 1 }-1 ,
Р {|„ = 0} = ^
,
п = 1, 2, . . .
Найти предельное распределение случайных величин
L — l l + " ' /+ g n ~ M ( l l + ' " + ln)
^ D ( i x+ . . . + | и)
4.126. П усть для
величины
....
пределены:
р
при
tt —*■оо.
каждого я = 1, 2, . . . случайные
независимы и одинаково рас
= V n } = Р {ЕГ> =
P{|f>
= 0}' = l — -т
т=
17
j/n 2
при любом / = 1
п. Найти М\f\ D\f> и предель
ное распределение случайной величины
б У Ч . - . + ё ? ’
113.
4.127*. П усть для каж дого п = 1, 2, . . . случайные величины
независимы и одинаково
распределены:
Р {|f > = V b ) = Р {|f> = ~ V h } =
P{gy» = 0) = « = i
при любом / = 1 ,
п. Найти М|/п>,
ное распределение случайной величины
T]„ = A - ± r i M У nD|f’
при
и предель
n -^ o o .
4.128. Случайная величина |„ имеет распределение
с дробно-линейной производящей функцией <р„ (z) =
_ Дд+(|— dn—ап)г ' 0 ^ а „ ^ 1 ,
0^ d„< l.
Какие
1
anz
невырожденные законы распределения F (х) могут быть
предельными для последовательности Р „( л: ) = р ||2- ^ л:^ ,
где А п — оо — некоторые нормирующие константы?
Какие условия надо наложить на последовательности
ап, dn, А п, чтобы lim F n (х) = F (x ), х > О?
оо
4.129. Случайные величины 1ц |2, . . . независимы,
неотрицательны и одинаково распределены:
P { I i > 0} = 1.
М|1 = р > 0 ,
D|x= a 2,
0 < о 2 < оо;
пусть N t = max {/г ^ 0: |х+ . . .
|х > t, то N t = 0). Показать,
— оо < х < оо,
что
t), t ^ O (если
для лю бого х,
l i mp { / V t < - + - ] / " - j = - t 4 f f e~ “ */*du.
I
M
P "
Pi
K lix —Joo
4.130. Случайные величины |x, |2, . . . , |„ незави
симы и имеют показательное распределение с пара
метром а:
Р { ! , . < л ) = 1— е~ах,
а
женные в порядке
х^О ,
г = 1, 2, . . . , п,
— значения |х, . . . , |„, располо
неубывания (вариационный ряд).
113
114.
Используя результаты задачи 3.46, показать, что еслип , т —>■оо и п — т —> оо, то:
а)
'
M6(e )= i ± £ i i i i n — — ,
а
п—т, ’
nt
_ 1+ ° ( 1)
т
ь'ь<т>
„
п(п—т)>
б) lim Р
< xj =
= И т Р { (а | (-) - l n ^ j ) Y
n Jlt^ r 1 < х } = Ф (*>,
— оо < х < оо.
4.131. Случайные величины £1?
и одинаково распределены:
Р{£i<*{ = ^ W,
i= i
независимы
п,
а £(1)
. . < £ (w) — их вариационный ряд (см. задачу
4.130). Д оказать, что если в некоторой окрестности
точки х = г0 сущ ествует непрерывная производная
р {х) = F' (х) > 0, то при т/п—> F ( 20), п
оо,
lim р ( т т щ
й ж
р <г,) <
* } - ф (х)-
4.132. Частицы последовательно размещаются в N
ячейках так, что вероятность попадания /-й ( / = 1 ,
2, . . . ) частицы в /-ю ( / ==1, 2, . . . , N) ячейку равна 1/N
и номер ячейки, в которую попадает частица, не за
висит от номеров ячеек, в которые попали предыдущие
частицы. П усть vk — порядковый номер частицы, после
размещения которой впервые число занятых (т. е. не
пустых)
ячеек
становится
равным k , и rk=
v*_i (v0= 0).
а)
Найти производящ ую функцию распределения тт
и
— V,},
б) Найти
lim max
JV-j-oo
r<m<N
m >k>l.
Р {тт > чи _ г — vra_ r},
r= 2,3,...
4.133. П усть случайная величина \к та же, что
в задаче 4.132. Найти предельное распределение слу
чайной величины vk — k, когда N —>■оо, k2/N —^K,
0 < Я < оо.
4.134. П усть выполнены условия задачи 4.132.
Найти асимптотические формулы для Mvm, Dvm и пре114
115.
дельноераспределение
V m
lY\Vm
, когда N —+ оо и
Г Dv/rc
a LN ^ m ^ , a 2N при некоторых а х, ос2, 0 < а 1 < о с 2 < 1 .
4.135.
Случайные величины
g2, . . . независимы
и имеют одно и то же распределение с характеристи
ческой функцией f(t). Доказать, что если при неко
торых С > О, 0 < а < 1 2 ,
f (t) = I — С \t \а (\ + о (I)),
то при п —^оо существует
случайных величин
Т —
Ья
t - + О,
предельное распределение
^2~
~***
Л^
1/а
Найти его характеристическую функцию.
4.136*. Случайная величина \ имеет абсолютно
непрерывное симметричное распределение с плотностью
р (х) ~ С |х\~а (\х\
с»), где С > 0, 1 < а < 3. Д ока
зать, что
°9
Me«e = l - 2 C | f | “ - l ( l + o ( l ) ) f —
J
О
Tr^du,
tl
t — 0.
4.137.
Случайная величина § имеет распределение
Коши с параметром а> т. е. имеет плотность распре
деления
р М
Н г Нг Ь 5*
- 0 0 < ^ < 00-
Показать, что характеристическая функция
рас
пределения | равна
Вывести отсюда и из за
дачи 4.136, что
С
J
о
1—COStl -аи
j
л
= U2
— 2
4.138.
Независимые одинаково распределенные слу
чайные величины
|2, . . . имеют абсолютно непре
рывное симметричное распределение с плотностью р (х),
непрерывной в точке х = 0, р ( 0 ) < о о . И спользуя ре
зультаты задач 4.135 — 4,137, найти предельное рас
пределение последовательности случайных величин
прй
п^ °°115
116.
4.139. Случайные величины £1Э |2, |3 имеют распределение Коши с параметром а; при этом
и
независимы, а Р{|3 = ^1}==1. Сравнить характеристи
ческие функции и функции распределения суммы ^ + Н2
независимых и суммы £x + E3 зависимых одинаково рас
пределенных случайных величин.
4.140. И спользуя результат задачи 4.137, вычислить
1а,ь(х )
Глава
J
(а2+ и 2) (Ь2 + ( х — и ) 2) '
5
ЦЕПИ МАРКОВА
Во введении к гл. 2 была определена общая схема
последовательности зависимых испытаний с исходами
1, . . . , i V , в которой вероятность появления цепочки
исходов i19 . . . , ik в испытаниях с номерами 1, .
представлялась в виде
Р (1 19 . . . , ik) = Р (h) Р (i2\h) - - -Р (ik lh - •где p (i/ \ ii. . л '/ - 1 ) ^ 0 — функции,
условиям
(5.1)
удовлетворяющие
N
'Е p { i j \ h . . . i j ^ ) = \
v =i
(5.2)
для лю бого
1 и любых i19 . . . , i/_ 1 £ {1, . . . , N }
В предыдущих главах, как правило, рассматри
вался частный случай однородной последовательности
независимых испытаний, когда функции
. Л у_х)=
= p (ij) не зависели ни от /, ни от iu . . . , ij_ la В этой
главе рассматривается другой важный частный случай
общей схемы (5.1), в котором для лю бого
2 и
любых г'х, . . . , i j _ x
Р (1/ Mi •••ly - i ) = Plj - V l/>
(5.3)
если выполнено (5.3), то говорят, что последователь
ность испытаний образует однородную цепь Маркова.
Условие (5.3) часто называют марковским свойством;
оно означает, что если исход какого-то испытания
фиксирован, то результаты испытаний, следующих за
выбранным, не зависят от результатов испытаний,
116
117.
предшествовавших ему. При построении математических моделей ряда реальных явлений предположение
(5.3) оказывается довольно естественным.
Для цепей Маркова начальному испытанию припи
сывают номер 0 (а не 1, как в (5.1)), исходы 1, . . . , 7 V
называют состояниями цепи, вектор
pw = { p?
р<
/?,) = ( р ( 1 ) , •••. р т
— вектором начальных вероятностей, а матрицу
f Pl l
••
Pi n \
P 4 P i 7 « м = 1= ( р! 1 . Л 2 . : 7
/ 2ЛЧ
\PNi
Pl2
PN2
• •
PNNJ
— матрицей вероятностей перехода. В силу (5.2) все
элементы матрицы Р неотрицательны и сумма элемен
тов каждой строки равна 1; матрицы, обладающие
этими свойствами, называют стохастическими.
Отметим, что все введенные здесь определения легко
распространяются на бесконечные последовательности
испытаний (цепи Маркова) с бесконечным множеством
исходов (состояний) {1, 2, . . . [ .
Из определений (5.1), (5.3) следует, что если
—
состояние цепи Маркова в момент t и
P i / ( 0 = Р {^>t = / I
= Р {&t + s = / I%>s = *}>
^ ^ 0»
— вероятность перехода из состояния i в состояние /
за t шагов, то матрица
^ Н 1 Р « 7 (* )1 1 и = 1 = ^ ,
р $ ), где p f' = P (gt = j), удоа векторы р «' = (р[‘\
влетворяют соотношению
p{t+s) _ pis)pt.
далее для любых 0 < /„ < tx < . . . < tk,
€{ 1
Р { L .=
= Ч> •••I
ia,
ik £
— iki=
/г
= р {^ . = и П
p ij^ i^ tj— b -d -
Таким образом, с формальной точки зрения исследо
вание многих свойств цепей Маркова сводится к изу
чению соответствующих свойств степеней матриц веро
117
118.
ятностей перехода (об одном из способов полученияявных формул для элементов степеней матриц см.
задачи 5.20, 5.21).
Важную роль при изучении цепей Маркова играет
классификация их состояний. Говорят, что состояние /
следует за состоянием i ( / —>/ ) , если
(0 > 0 для
некоторого целого ^ > 0; если i —+ j и j - + i , то с о
стояния i и / называют сообщающимися (i <-»/). Если
для состояния i найдется такое состояние / = / ( / ) , что
i - ^ j , но /у и * (т. е. pf i (t) = 0), то состояние i назы
вается несущественным; в противном случае состояние i
существенное. М ножество всех существенных состояний
с помощью отношения <-» (нетрудно проверить, что
это отношение является отношением эквивалентности)
разбивается на классы сообщающихся существенных со
стояний; переходы траектории цепи из одного такого
класса в другой невозможны. Множество несущест
венных состояний тоже разбивается на классы сооб
щающихся состояний; траектория цепи Маркова может
выходить из любого такого класса, но, выйдя из
такого класса, вернуться в него уже не может. Если
множество состояний цепи Маркова конечно, то с
вероятностью 1 траектория цепи рано или поздно вы
ходит из множества несущественных состояний и после
этого остается в одном из классов существенных сооб
щающихся состояний.
Говорят, что класс А сообщающихся состояний
периодический с периодом d > 1, если для состояния
i £А
{t: рц (t) > 0 }cz{d , 2d, 3d, . . . }
(5.4)
и любое число dx > d не удовлетворяет (5.4); опреде
ленное по формуле (5.4) число d зависит от класса А ,
но не от выбора элемента i £ Л . Если (5.4) выполняется
только при d = 1, то класс Л называют апериодическим.
П усть все состояния цепи Маркова \t с матрицей
вероятностей перехода Р образуют один апериодичес
кий класс сообщающихся состояний. Тогда существует
такое целое число tQ, что при любом t ^ t 0 все эле
менты матрицы Р1 положительны и справедлива сле
дующая
Теорема. Если для цепи Маркова с N < оо состоя
ниями при некотором tQ> 0 все элементы матрицы Р**
118
119.
положительны, то существуютlim Pij (t) = Яу > 0,
i, / € { 1. .
/—
>00
Распределение л = (л1,
я^) не зависит от на
чального состояния i цепи
и называется предельным
или финальным распределением
Кроме того, рас
пределение я стационарно, т. е. яР* = я для лю бого
f = l, 2, . . . В случае, рассмотренном в теореме, ста
ционарное распределение единственно и совпадает с
предельным; если цепь Маркова имеет несколько апе
риодических классов существенных сообщающихся
состояний, то существует много стационарных распре
делений и предельное распределение зависит от началь
ного; если цепь содержит несущественные состояния,
то соответствующ ие им предельные вероятности равны 0.
Наконец, если все состояния цепи Маркова
об
разуют один класс периода d > 1, то предельного
распределения, вообще говоря, не существует; сущ ест
вуют только
lim p ij( td + k) = n l %
t—
>оо
ii / € { 1 » •••» N\y fe = 1, 2, . . . 9 d.
5.1. Матрица вероятностей перехода цепи Маркова
имеет вид
/0,1
0,5
0,6
0,2
0,4\
0,2 ).
\ 0 ,3
0,4
0,3/
Распределение по состояниям в момент времени £ = 0
определяется вектором (0,7; 0,2; 0,1). Найти:
1) распределение по состояниям в момент t = 2;
2) вероятность того, что в моменты £ = 0, 1, 2, 3 со
стояниями цепи будут соответственно 1, 3, 3, 2;
3) стационарное распределение.
5.2. Пусть l t — номер состояния в цепи Маркова
в момент времени t\ Р(|0= 1 ) = 1 , и матрица вероятно
стей перехода имеет вид
/3/7
3/7
1/7 \
1/11
2/11
8/11
\ 1 / 11
3/11
6/11/
;
119
120.
положим1,
если
£#=1»
{ 2, если Ъ ,ф1.
Показать, что последовательность т|г является цепью
Маркова. Найти ее матрицу вероятностей перехода.
5.3.
Случайные величины |t, t = 1, 2
незави
симы и
P(Ht = l ) = p,
P(Ef = — 1 ) = 1 — р = ^.
Положим 11о = 0; т)<+х = Tlt + it+i- Является ли после
довательность г], цепью Маркова? Найти P(y\t = m),
т = О, 1, 2, . . .
5.4.
П усть |t, / = 1 , 2, . . . , — независимые случай
ные величины, P(|t = l ) = 1— Р(|, = — 1) = р. Являются
ли цепями Маркова последовательности случайных ве
личин:
1) % = S#l t + i ,
2) Л# = Ы 2 ■• • St;
3) % = <P(S#, St+i), где ф (— 1, — 1 )= 1, ф (— 1, 1)= 2,
Ф (1, — 1) = 3 , Ф ( 1 ,
1) = 4 ?
Для цепей Маркова найти вероятности перехода за
один шаг.
5.5. В N ячейках последовательно независимо друг
от друга равновероятно размещают частицы. Пусть
р0 (п) — число ячеек, оставшихся пустыми после разме
щения п частиц. Показать, что последовательность
|л0(я), п = 1, 2, . . . , является цепью Маркова. Найти
вероятности перехода.
5.6. В N ячейках независимо друг от друга раз
мещаются комплекты, состоящие из т частиц. Частицы
одного комплекта размещаются в ячейках по одной,
и все возможные выборы т мест из N имеют одина
ковые вероятности. Обозначим через (х0(я) число ячеек,
оставшихся пустыми после размещения п комплектов.
Показать, что последовательность |л0 (п), п = 1, 2, . . . ,
является цепью Маркова. Найти вероятности перехода.
5.7. Матрица Р = \\р^\\^i==1 с неотрицательными
элементами называется дважды стохастической, если
Р /i + Р /2 +
• • • + P i N ~ Р 1 / + Р 2 / + • • • + Pn i — 1
Для
лю"
бого / = 1, 2, . . . , N. Показать, что если цепь Мар
кова
с состояниями 1,
N имеет дважды стоха
120
121.
стическую матрицу вероятностей перехода P = \p-jто равномерное распределение на множестве {1, . . . , N )
является стационарным для цепи £t.
5.8. Пусть £0, £lt . . . — цепь Маркова с множеством
состояний {1, 2, 3}, матрицей вероятностей перехода||р/7||
и стационарным распределением jty. Показать, что если
P ll ~ Р 2 2 = Рзз ~ ^
И 2Xj = Jtg = JXg — 1/3 » ТО Pi2 = P 2 3 ==P 3 i
И Pl3 = /*21 = Рз2'
5.9. П усть гц, г]2, . . . — последовательность незави
симых одинаково распределенных случайных величин,
и f ( x 1 у) — функция, принимающая значения в множе
стве {1, . . . , N\. Является ли последовательность слу
чайных величин
So (P(So = k) = p f \
6t+1 = / ( E „ л ,+1),
t = 0, 1, 2, ...,
цепью Маркова?
5.10. П усть r]0, rj1, r]2, . . . — последовательность
независимых случайных величин, имеющих равномер
ное распределение на отрезке [0, 1]. Показать, что
для любого начального распределения р {0) = (pi0), . . . , р $ )
и для любой матрицы переходных вероятностей Р =
Hi Pi/fi,i=i можно указать такие функции /( х , у) и
g { y ) { x £ { 1, . . . , М [ , у 6 [ 0 , 1]), что последовательность
1о = ё(Цо)у
=
rlt+i)» < = 0, 1, . . . , будет цепью
Маркова с начальным распределением р {0) и матрицей
вероятностей перехода Р.
5.11. Игральная кость последовательно переклады
вается с одной грани равновероятно на любую из
четырех соседних независимо от предыдущего. К ка
кому пределу стремится при t — > 00 вероятность того,
что при t-м перекладывании кость окажется на грани «6»,
если сначала она находилась в этом же положении?
5.12. Матрица вероятностей перехода |Ну|| цепи
Маркова £* с п + 1 состояниями имеет вид: р и = 1 — а,
г’ = 1, 2, . . . , n + l ; pij = а/п, 1 Ф } . В процессе, начав
шемся из состояния &, к ф п - \ - 1, обозначим через %п
момент первого попадания в состояние п + 1. Подобрать
последовательность А п (А п
оо при п —►оо) так, чтобы
существовал предел
lim Р (тп/Ап > х ) ,
П-> <Ю
и найти его.
121
122.
5.13. П усть gj, i 2, . . . — независимые одинаковораспределенные
случайные
величины,
Р
= 1}•=
= Р { i i = — 1} = 1/2; z0 = 0 , zk = zk- x + l k, k = 1,2, . . . По
ложим %N = min {n ^ 1: |zn |= N\. Найти Мт1( Мт2, Мт3.
5.14. Пусть последовательность z0, z,, . . . опреде
лена как в задаче 5.13. Показать, что Мтдr= N 2.
5.15. Движение частицы по целым точкам отрезка
[0, N ] описывается цепью Маркова clV + 1 состояниями
и вероятностями перехода за один шаг P o i= P a w = ^
Pi, ,-+х = Р. Pi, i - i = l ~ Р = Я (« = 1> — 1). Пусть
| ( t )— положение частицы в момент t и T = m in {/: l( /)= /V }.
Показать, что
т * = М {т | 1 (0 ) = £} =
J ^ ( ( *УЧ*)*)-£± »+*
{ (N -k )(N + k )
(p = q = 1/2).
5.16. Движение частицы по целым точкам отрезка
[0, Л/] описывается цепью Маркова с N + 1 состояниями
и вероятностями перехода за один шаг р 00 = PNN= 1,
P i,i + l = P> Pi, i - 1 = 4 (i=l . 1). Пусть 1 ( 0 —
положение частицы в момент t , p {/(t) = P {^ (t) =
= /| g (0 ) = i}. Найти вероятности поглощения частицы
в точках 0 и N:
4 0,= lim /7ft0 (0 .
t -*■00
"4№= lim pkN(t).
t—
► 00
5.17. В городе N каждый житель имеет одну из
трех профессий: Л, В, С. Дети отцов, имеющих про
фессии Л, В, С, сохраняют профессии отцов с вероят
ностями 3/5, 2/3, 1/4 соответственно, а если не сохра
няют, то с равными вероятностями выбирают любую
из двух других профессий. Найти:
1) распределение по профессиям в следующем по
колении, если в данном поколении профессию Л имело
20% жителей, В — 30%, С — 50%;
2) предельное распределение по профессиям, когда
число поколений растет;
3) распределение по профессиям, не меняющееся
при смене поколений.
5.18. По двум урнам разложено N черных и N бе
лых шаров так, что каждая урна содержит N шаров.
Число черных шаров в первой урне в момент £ = 0,
122
123.
1 , 2 , . . , обозначим \t. В каждый целочисленный моментвремени случайно выбирают по одному шару из каждой
урны и меняют их местами. Показать, что
является
цепью Маркова со стационарным распределением
n k= ( C k
N)VC»N,
fe = 0 , 1, . . . , N.
5.19. Матрица вероятностей перехода Р и распре
деление q по состояниям в момент t = 0 цепи Маркова
имеют вид
' 3/ 12
2/12
1/ 12
3/12
1/ 12
2/12'
1/ 12
1/ 12
3/12
1/ 12
4/12
2/12
р__
0
0
3/4
1/ 4
0
0
^ “
0
0
1/2
1/2
0
0
0
0
0
0
1/ 3
2/3
, 0
0
0
0
2/3
1/ 3
? = (V., х/ 2,
’
j
о> о» о).
Найти:
а) несущественные состояния;
б) математическое ожидание времени т до выхода
из множества несущественных состояний;
в) вероятности p f \ p f ) попадания в классы состоя
ний о с = {3 ; 4}, Р = {5, 6}, если начальным состоянием
является i € {1, 2};
г) предельное при t
оо распределение по состоя
ниям, т. е. величины nk= l imP(Et = &).
t -> О
О
5.20. Показать, что если все собственные числа
. . . , Хп матрицы А = |а,7 ||" ,-=1 различны, то эле
менты матрицы А т= I | £ j=1 представляются в виде
П
a \ f = 2 Сц'МР*
т = 1 , 2, . . .
*=i
5.21. Показать, что если матрица А = ||ау/ ||£/в1
имеет собственные числа
...,
причем кратность Яу
равна Sj, sx+ •••+ s r = n, то элементы матрицы А т=
=||flJ7,)||?t/- i представляются в виде
г
sk~l
а№ = 2 ЭД1 2 4 / ’ l)ml ,
ft=l
/=о
m = 1,2, . . .
5.22. Используя задачи 5.20 и 5.21, показать, что
получение формулы для вероятности перехода за п
шагов из состояния i в состояние / в цепи Маркова
123
124.
с N состояниями может быть сведено к нахождениюсобственных чисел матрицы Р = ||р/у||£/^вероятностей
перехода за один шаг, вычислению Р, Р 2,
Р м~х
и решению системы линейных уравнений.
5.23. Матрица вероятностей перехода Р = ||р,у|| цепи
Маркова
с состояниями 1 и 2 определяется форму
лами
Рп = 1— « ,
р ,2 = а,
/7и = р,
р22= 1— р.
Найти вероятности p {j ( t ) перехода за время t и ста
ционарные вероятности я,.
5.24. Для цепи Маркова |(, рассмотренной в зада
че 5.23, обозначим через vx (/) число попаданий в со
стояние
1 за время t. Показать, что для любого
/ = 1, 2 при t —*■ оо
M h (OI&.=/}=£fpf(i-H>0)).
D { v x (O|io = / } = 0 (^ ).
5.25. П усть выполнены условия задачи 5.24. Пока
зать, что для любого е > 0 и любого / = 1, 2
р •{ I
I> е 1
5.26. Пусть цепь Маркова
имеет матрицу вероятностей
удовлетворяющую условию
с состояниями 1, . . . , N
перехода P — \Pij\i,i=u
N I
II
max
I
Р
/
г
т
1< i< N “
I
I
Показать, что если я = (я х,
распределение цепи gf , то
. . . , я д.) — стационарное
N
5.27.
П усть \t и
цепи Маркова с матрицами
вероятностей перехода Р = ||р/7 ||£/=1 и Р' = ||Pi/llu-=i
соответственно, а я = (я х, . . . , Ядг) и я ' = (я(, . . . , я^) —
стационарные распределения этих цепей. Следует ли
из близости элементов матриц Р и Р' (например, из
124
125.
Nмалости
величины
2
\Pi/— Pij\)
близость
векторов
п и л '?
5.28*. Частица совершает случайное блуждание по
множеству точек плоскости с целочисленными коорди
натами. За единицу времени частица перемещается на
единичное расстояние параллельно одной из осей коор
динат. После прохождения каждого единичного отрезка
частица выбирает направление дальнейшего движения:
либо продолжать движение в том же направлении,
либо повернуть налево, либо направо (каждый из этих
вариантов выбирается с вероятностью 1/3 независимо
от предыдущих
движений
частицы). Пусть z n =
= (z%\ z^) — положение частицы в момент п. Найти
при условии, что z 0 = (0, 0), z 1 = (l, 0).
5.29*. Случайные величины
|2, . . . независимы,
принимают значения 1 и — 1 с вероятностями р и
<7 = 1 — р соответственно, и
S0= 0,
S n=
-f- . . . +
n — 1, 2, . . .
Обозначим через v число таких /г, что S „ = 0.
а) Показать, что если p ^ q , то P { v < o o } = l ;
б) показать, что если р = q = V2, то P { v = o o } = l.
5.30*. Независимые случайные векторы £„ = (!„, l t . . .
...,
5) С jRs, п = 1 , 2 , .. ., имеют независимые ком
поненты и Р
1} = Р{ £ „ , / = — 1} = у .
п = 1, 2, . . . Положим 5^ = ^ + . . . + 1 п, п = 1 ,2
и обозначим через v число таких п, что S n = (0,. . . , 0).
Показать, что Р { v = о о } = 1 при s = 2 и что Р { v < o o } = 1
при s ^ 3.
Глава
6
ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
В математической статистике исследуются выводы,
которые могут быть сделаны на основе эмпирических
данных. Случайной выборкой объема п (или просто
выборкой) называется случайный вектор
*^li
^2» •••»
(6*1)
где
независимы и имеют одну и ту же функцию
распределения F (x ) = P ( х ^ х ) . Случайная выборка
125
126.
является математической моделью последовательно проводимых измерений или наблюдений.
Обычно для выборки (6.1) известен только тип рас
пределения (например, нормальный), но неизвестны па
раметры, от которых зависит распределение. В этом
случае по выборке требуется каким-либо образом опре
делить приближенные значения неизвестных параметров.
Пусть Р (x t ^ х) = Fi (х, 6). Оценкой неизвестного
параметра 6 назовем произвольную функцию 0* =
= 0 „(* 1, . . . , х п). Оценка 0^ является несмещенной
оценкой 0, если М0* = 0. Если 0* при п —*- оо сходится
по вероятности к 0, то оценка 0* называется состоя
тельной.
Может оказаться, что существуют такие функции
=
•••• *«) и
.......... *»). что р (9п <
< 0 < 0 И) = 1 — 2а одинакова при всех значениях неиз
вестного параметра 0. В этом случае интервал (0„, 0И)
называют доверительным интервалом, и вероятность
1— 2ос того, что интервал (0„, 0„) накроет неизвестный
параметр 0, называют доверительной вероятностью.
Если при п —> оо
р (е „< е < ё „)-1-
2а
и предельная вероятность не зависит от 0, то интервал
(0„, 0J будем называть асимптотическим доверитель
ным интервалом.
В случае, когда выборка (6.1) соответствует нор
мальной случайной величине § с параметрами М| = а,
DS=< j 2, можно построить для неизвестных параметров
а и а2 доверительные интервалы.
Пусть |0, |1# . . . , l^ — независимые нормально рас
пределенные величины с параметрами (0, 1). Положим
%fi = i i + ••• +
т
Законы распределения этих величин называются соот
ветственно распределением х2 и распределением Стьюдента с п степенями свободы. Определим величины
ta,n и %а, л как решения уравнений
р К , > ta, „) = а,
126
Р (уД > у1, „) = а.
127.
Тогда (см. [10])Р ( x — ta, n- i - y = < a < x + tat „ - 1 - ^ = - ^ = 1— 2а,
Р (% 1 -а, „-х <
< Х&. n - i ) = 1 - 2а,
где
П
* = 7 Г ( * 1 + •••+*«)>
k~ 1
Отметим, что в рассматриваемом случае х и s2 независимы.
Случайные величины (6.1), расположенные в по
рядке возрастания их значений,
* < £ > < * < « < ••• <*<„>
(6.2)
называют вариационным рядом. В частности,
Хф = min \xt , . . . , х п\,
х (п) = шах {x lf . . . , *„}.
Эмпирической функцией распределения называется функция F „{x ) = kln, если
*<а+1 >]> k = 0, 1,
п,
где х (0) = — оо, «(„+!) = оо- Нетрудно проверить, что
F n(x) является несмещенной и состоятельной оценкой
F (х) при любом х.
Одним из методов получения оценок является метод
наибольшего правдоподобия. П усть (6.1) — независимая
выборка, соответствующая случайной величине
име
ющей плотность распределения р%(х, 0Х, . . . , 0ft). Функ
цией правдоподобия называется функция
п
L
. . . , х п, 01э . . . , 0jj) = J J
t= 1
(Xf) 0lf . . . , 0^).
Оценками наибольшего правдоподобия параметров 01?. . .
. . . , 0А называется решение 0^, . . . , 0£ системыурав
нений
д InLi
Г\
“ёёГ = 0,
1
1
1 = \,
L
k.
Оценки наибольшего правдоподобия при достаточно
общих условиях (см. [7]) оказываются состоятельными
и асимптотически нормальными. Аналогично опреде
ляется функция L для дискретных случайных величин.
127
128.
Другой круг задач математической статистики связанс проверкой различных гипотез. Пусть о выборке (6.1)
выдвинуто два предположения (две гипотезы):
Я 0: (х19 . . . , х п) имеет распределение Р0,
Н г: {хи . . . , х п) имеет распределение Р1Э
где Р0, Pi — два известных распределения.
Тогда правило выбора одной из этих гипотез, или
статистический критерий, определяется подмножеством
В множества значений (х19 . . . , х п) и имеет вид: если
(х
. . . , х п) £ В , то принимается гипотеза H lt в про
тивном случае — Н^. Вероятность а = Р0 (В), т. е. веро
ятность принять гипотезу Н 19 когда в действительно
сти верна Я 0, называется ошибкой 1-го рода. Вероят
ность Р = РХ(В), т. е. вероятность принять Я 0, когда
верна Я г, называется ошибкой 2-го рода. Если множе
ство В задано в виде
{(* i
x n)£ B \ = {r\n = r\n (xlt
х п) > С \ ,
то функцию Цп = г[п(х 1 , . . . , х п) называют статистикой
критерия. Например, пусть р^{х) плотность распреде
ления каждого х { при гипотезе Я 0 и / ^ ( ^ — соответ
ствующая плотность при гипотезе Н г. Положим
Pi (* i ) Pi Ы
ln
••• Pl (хп)
P o ( * i ) P q (x 2) . . . P o ( x n) *
Согласно критерию Неймана — Пирсона при ч )п > С
(С — некоторая постоянная, определяемая по ошибке
1-го рода) принимается гипотеза Я 1Э а в противном
случае — Я 0. Этот критерий среди всех критериев с фик
сированной ошибкой 1-го рода имеет наименьшую
ошибку 2-го рода (см. [7], § 35.3, с. 576, 577). Анало
гично формулируется критерий для дискретных рас
пределений.
Иногда формулируется только одна гипотеза о вы
борке (6.1). Эту гипотезу нужно либо принять, либо
отвергнуть. П усть, например, гипотеза состоит в том,
что выборка (6.1) соответствует случайной величине |
с Р (| ^ л :) = ^(л :). Для статистической проверки этой
гипотезы используется так называемый критерий %2.
Разобьем числовую ось на г + 1 непересекающихся интерг+1
валов Дг, Д2,
Аг+1, и Д , = ( — с», оо). Положим
i= 1
pft = P ( ! € A ft), 6 = 1
r + l . Обозначим через mk
128
129.
число Х[, попавших в ЛА. Статистикойявляется величина
г+1
„
_ V (mi ~ nPi)*
r v=\
npi
'
критерия %*
Оказывается, что (см. [10], гл. 7, § 3) для любого х
при /г — оо
Р(ЛЯ. Г < * ) - * Р ( Х ? < * ) -
(6.3)
По критерию х2 предположение о законе распределения
отвергается, если
г > С. Величина С выбирается так,
чтобы вероятность Р (r]Wj г > С) = а была мала. При таком
выборе С в случае rjrtj г > С говорят, что гипотеза
отвергается с уровнем значимости а. Используя пре
дельное распределение (6.3), можно положить С = х а,п
где Р (%2
Г > Ха, г) =
В приложениях интервалы ДА,
f e = l , . . . , г + 1 » выбирают так, чтобы число членов
выборки в каждом из них было не очень малень
ким (например, npk не меньше 7). Если распределение
F^(x) зависит от неизвестных параметров, то вероятно
сти pk = P ( g £ A ft) вычисляют, заменяя параметры их
достаточно хорошими оценками. В этом случае в пре
дельном распределении (6.3) г должно быть уменьшено
на число неизвестных параметров (см. [7], § 30.3, с.
460— 463).
6.1. Пусть х 19 х 2, . . . , х п— случайная выборка
с hAxk = a, Dxk = <jz, М (Xfc — а)4, < о о , f e = l , . . . , п.
Найти математическое ожидание величины
s2 = п — \ 2 1 (x k — x )2
k= i
( х — 7Г 2 1 x k ) »
\
k—\ f
является ли s2 состоятельной оценкой а2?
6.2. Найти математическое ожидание и дисперсию
эмпирического
момента
mr = Xl^~
независимой
выборки, соответствующей случайной величине | с
Мl k = ak9 1 < £ < 2 г .
6.3. По неоднородной выборке х19 . . . , х п9 где хк9
ft = 1, . . . , п, независимы, tAxk = a, Dxk — а| (aft известны),
найти
несмещенную
линейную
относительно
xk
(k = l 9 . . . » п) оценку а9 параметра а с наименьшей дис
персией.
129
130.
6.4. П усть х п , . . . , х {П{ (i = l, . . . , I) — независимые нормально распределенные величины с парамет
рами (а, <т?);
k= 1
/г= 1
является ли оценка
-
V . -
If
" “ Й СЛ’
c' " l ! T 3 T T f
несмещенной оценкой параметра а?
6.5. П усть х 19 . . . ,
— выборка, Мх| < оо, & =
= 1, . . . , п. Положим
л
л
x = j H x k>
*=1
s2 = ^ i S ( ^ - ^ ) 2Л=1
Найти
lim Р ( * 7 ^ _ х < дЛ .
Л —>■ оо
\ S
/ | / n
/
6.6. П усть (х1? t/j), . . . , (ял, у„) — независимая вы
борка, соответствующая случайной величине (§, г]), т. е.
=
ц ^ у ) - Показать, что ве
личина
л
« и = 7 Г П И (** “ *) (Уь ~ У)>
k= 1
где
л
* =
k=1
л
У=\ЦУк>
k—1
является
несмещенной
и состоятельной
оценкой
cov (g, Г|).
6.7. Пусть [лЛ— число успехов в п испытаниях схемы
Бернулли с вероятностью успеха р в каждом испыта
нии. Методом наибольшего правдоподобия найти оценку
р* параметра р. Доказать ее несмещенность и состоя
тельность.
6.8. П усть |лЛ—- число успехов в п испытаниях схемы
Бернулли с вероятностью успеха р в каждом испыта
130
131.
нии. Построить для р асимптотический доверительныйинтервал с доверительной вероятностью 1 — 2а.
6.9. Используя таблицу случайных чисел, получить
реализацию выборки х 1У . . . , х п, где х к равномерно
распределены на отрезке [0, 1] (значения х к взять с тремя
знаками; п = 50). Найти:
а) вариационный ряд х {1) ^ х {2) ^ . . . ^ х ш \
б) эмпирическую функцию распределения (построить
ее график и график теоретической функции распреде
ления);
в) х = ^ ( х 1+ . . . + * л ) (сравнить с Мл^);
п
г) s2 = ^— j- У , (х ь — x f (сравнить с Dxft).
k= 1
6.10. Используя таблицу нормальных случайных чи
сел, получить реализацию выборки х 1У . . . , х пУ где х к
имеет нормальное распределение с параметрами a = tAxk=
= 0,5, <j2 = Dxk= l \ п = 50. Найти: а) вариационный
ряд, б) эмпирическую функцию распределения, в) х у
г) sa (см. задачу 6.9).
6.11. По выборке, полученной в задаче 6.10, по
строить доверительный интервал для а (считая а и а
неизвестными) с доверительной вероятностью 0,95.
6.12. Используя метод наибольшего правдоподобия,
найти по выборке х 1У . . . , х пУ где Р (xk = tn) = ^ e ‘ xy
т = 0, 1, . . . , оценку X* параметра X. Будет ли эта
оценка несмещенной и состоятельной? Найти MX*, DX*.
6.13. Пусть х 1У х 2У . . . , х п — выборка, соответствую
щая показательному распределению с параметром X.
Найти оценку максимального правдоподобия X* для X.
Вычислить М
,
D
.
6.14. Для оценки параметров а, Ъу с имеются три
независимые выборки а1У . . . , ап\ Ъ1У . . . , Ъп\ с1У . . . , сп.
Известно, что с = а + Ь и величины aiy biy c t распреде
лены нормально с Ма£-= а, МЬ£-= Ь, Мс { = с. Дисперсии
Dа£-= а 2, DЬ£-= а^, DС; = о 2 известны. Найти:
а)
оценки наибольшего правдоподобия а*у Ь*у с* па
раметров а, Ь, с у используя для каждого параметра
только соответствующую ему выборку, а также найти
Ма*, Мb*, Me*, Da*, Dfc*, Dс*\
132.
б) оценки наибольшего правдоподобия а**, Ь**, с**,используя сразу три выборки и связь с = а + Ъ9 и также
найти Ма**, Mb**, М с**, Da**, Db**, Dc**\
в) отношения Da*/Da**, Db*/Db**, Dc*/Dc**.
6.15.
Имеется ml независимых случайных величин,
равномерно распределенных в области G czR n:
■II» •••» ?1*|я»
*
1» * * *» I-
Найти несмещенную оценку Ь*2 дисперсии Dr^ Построить
асимптотический при I —> оо доверительный интервал
для а с доверительной вероятностью 1— 2а.
6.16. Для величины А = а + |За + уЬ получены оценки
А{ = a-\-$z 1 + Тгз»
А1 = а -{-$ г 2-{- yz3,
где а, (3, у — известные постоянные, г19 z29 г3 — незави
симые оценки неизвестных параметров: Мг3 = Ь,
=
= Мг 2 = а , D2 / = <j?, i — 1, 2, 3. Подобрать постоянные
с19 с2 так, чтобы оценка А* = с1А1 + с2А1 была несме
щенной и имела среди несмещенных оценок наимень
шую дисперсию. Найти дисперсию полученной оценки.
6.17*. П усть г19 г 29 г3 — несмещенные оценки пара
метра a; Dzi = 1 (i = 1, 2, 3), cov (zlf z2) = p, cov (zi9 z3) =
= 0, t = l, 2. Найти несмещенную линейную оценку
z = C i Z i + c222+
2
с наименьшей дисперсией и диспер
сию этой оценки. Рассмотреть случаи:
с з
з
а) |р |< 1,
б) р = — 1,
в) р = 1.
Объяснить результаты в случаях б) и в).
6.18.
Функция у = А х измерена в точке х { ( i = 1,
. . . , k) п ( раз. П усть результаты измерений y {J (/«= 1,
. . . , ni9 i = l , . . . , &) не коррелированы и имеют вид
где М6<7 = 0, D6,7 = a2. Найти оценку А* параметра
А 9 используя метод наименьших квадратов, т. е. ми132
133.
нимизируя по А выражениеПА) = 2
Ъ Ъ ц -А х ,)'.
Ы 1 ]=1
Найти МЛ* и DA*.
6.19. В предыдущей задаче обозначим
У1 = - ^ Ц у ф » = 1. •••> Ь.
/=1
Подобрать
. . . , ск так, чтобы несмещенная оценка
А* = сгу г + с2у 2+ • .. + ckyk
имела наименьшую дисперсию. Найти DA* при наилуч
шем выборе с19 . . . , ck.
6.20. Из урны, содержащей неизвестное число ша
ров N (шары занумерованы), производится выборка
объема п с возвращением. Для оценки числа N исполь
зуется величина l/rj„, где
N
Г1и= П(п— 1) S
(£*
k= l
О»
— число шаров с номером k в выборке. Найти Mr],,
и асимптотическую формулу для Drj„ при n, N —*оо,
a = n/N = const.
6.21. П усть х а ) ^ . . . . ^ х (п)— вариационный ряд,
построенный по выборке x lt . . . , хп, где x k независи
мы и равномерно распределены на отрезке [а, Ь].
Являются ли оценки а* = х (1), Ь * ~ х (П) несмещенными
оценками а и Ь? Найти Ма*, Mb*, Da*, Db*.
6.22. П усть х {1) ^ . . .
— вариационный ряд,
построенный по выборке х 19 . . . , х п, где
имеет п о
казательное распределение с плотностью р (х) =<хе~(ХХ9
х > 0 . Найти М *(1), М *(я), D*(1), Dx{n).
6.23. П у ст ь * !, . . . , * „ — выборка и x {i) ^ . . . ^ х {п) —
ее вариационный ряд. Положим
Q *
_
~
____ * 1 +
Vi = x -----------
• • +
* »
Q *
______* < 1 > + * < Л >
, v2 —
2------
Найти M0fe, D0* (fe = l,2 ), если:
а) xk равномерно распределены на отрезке [а, Ь],
б) Pxk (x ) == a e^(KXf х > 0 .
133
134.
6.24. П усть х {1)^ . . .— вариационный ряд,
построенный по выборке х и , ♦♦, х п, где x k имеет
плотность распределения, равную ес~х при х ^ с > 0.
Является ли оценка с* = х {1)— \/п несмещенной и с о
стоятельной оценкой с? Найти Мс* и Ос*.
6.25. Используя критерий %2, проверить гипотезу
о том, что выборка, полученная в задаче 6.9, соот
ветствует равномерному распределению на отрезке
[0, 1]. Уровень значимости а = 0,05.
6.26 Используя критерий %2, проверить гипотезу о
том, что выборка, полученная в задаче 6.10, соответ
ствует нормальному распределению; параметры а и а
считать неизвестными. Уровень значимости положить
равным 0,05.
6.27. Найти статистику г\п критерия Неймана— Пир
сона для различения по выборке х 19 . . . , х п гипотез
Я 0: х к распределены нормально с параметрами (а0, а 2),
Н г: x k распределены нормально с параметрами (аг, а2).
6.28. Найти статистику цп критерия Неймана— Пир
сона для различения по выборке х 19 . . . , х п гипотез
Я 0: P (x k = i) = p?\ i = 1, 2, . . . , N ,
Hi -
p (x k = i) = P ? )> i = = l >2 , •••> H-
6.29. Статистика £„ при гипотезе H { (t = 0,1) имеет
нормальное распределение с ME„ = azn, 0\п~т \\
а0 < аг. Гипотеза Н г принимается, если |„ > С, в про
тивном случае принимается Я 0. Найти: а)постоянную
С = Са так, чтобы ошибка 1-го рода была равна ос;
б) формулу, связывающую а и |3„; в) lim (Зл.
п -+■ со
6.30. П усть х 1У . . . , х п— выборка. Гипотеза Я 0
состоит в том, что Х{ равномерно распределены на
отрезке [0, 1], а Я х— в том, что x t имеют плотность
распределения £ (* ); g ( x ) z £ 1 при
g (x ) = 0
при х (£ [0 , 1]. Обозначим р0 число интервалов среди
\_W'
(fe = 0, 1,
...,
N — 1), не содержащих ни
одного x t. При гипотезах Я,- (i = 0,1) найти а , =
= lim (М р0/Я ), когда п —* оо, n/N = у = const.
6.31. При гипотезе Н и определенной в задаче 6.30,
найти lim
N
134
-^2- = о?, если n/N = y.
оо
/v
135.
ЧастьГлава
II. УКАЗАНИЯ
1
1.3. Предположить, что все расположения книг равновероятны.
Найти число расположений книг с фиксированным расположением
трехтомника.
1.4. За множество Q принять множество всех последователь
ностей длины 3, составленных из символов Г — «герб», Р — «ре
шетка».
1.8.
Для простоты считать, что в каждой буквенной серии име
ются все 104 номеров от 0000 до 9999. (На самом деле номер 0000 не
выдается. Кроме того, в некоторых сериях не все номера выданы,
а часть номеров отсутствует в связи со снятием автомобиля
с учета.)
1.10. Положим Л/ = {выбранное число а делится на а /}. Вос
пользоваться тем, что
р1о/'}-р{Дл'}=|-рЦ 4
Далее применить формулу (1.12).
1.11. Поскольку а2 = 1 (mod 10) тогда и только тогда, когда
а = 1 (mod 10) или а = 9 (mod 10), надо подсчитать среди чисел
1, 2, . . . , N число тех, которые в десятичной записи оканчиваются
на 1 или 9. Положив A f= 1 0 £ -f-/, рассмотреть следующие случаи:
/ = 0, К / < 9, 1= 9.
1. 12. Если среди чисел 1, . . . , N есть ровно т чисел, даю
щих при делении на г остаток q , то (т— l ) r - \ - q ^ N < m r - \ - q ,
т. е. m r ^ N - \ - r — q < (m-\-\)r.
1.14. Введем обозначения для следующих событий!
Лл = {| делится на k},
£ fe = {rj делится на k},
См = {числа ^ и т] взаимно просты}.
Тогда С м =
U
(А Р[\ВР), где объединение берется
по всем
простым числам р, не превосходящим N . Вероятность Р (Сдг) на
ходится по формуле (1.12). Воспользоваться решением задачи 1.10
135
136.
и равенством A pi П А Рг f| . . . f| Apr = Аргр 2 . . . / vвеРным Для лю‘
оо
<5ых простых pi < Р 2 < •• • < Рг- Показать, что
= ^
N-+°o
П=Х
1.16. Искомая вероятность р д г= Ajy/N2, где А # — число точек
плоскости с целыми координатами (я, у), удовлетворяющими усло-
зх
виям х ^ \ у у
1, х 2-\-у2 < N 2. Показать, что Л д г ~ ~ Х 2
N — > оо.
1.16. Число
тогда, когда
£+*1 будет (п — * + 1)-значным тогда и только
1 0 » - * < g + n < 10»“ *+xf
о
при
(1)
Апt k
поэтому pn- k + 1=
где
A n , k — число точек плоскости с це
лыми координатами (х, у), 0 * ^ х , у*^\О п— 1, для которых вы
полнены неравенства ( 1).
1.17. Произведение £ и rj будет (2п — *)-значным тогда и только
тогда, когда
102 " - * - i < g n < Ю2»-* ,
(1')
&п, k
поэтому P2n - k — ~^ i n » где Вп^ — число точек плоскости с целыми
координатами (х, у), 0 < < *, у< ^ 10w— 1, для которых справедливы
неравенства (Г ). Показать, что Bn t k ~ B k * 102w при п — ^оо,
где
B k— площадь
части единичного квадрата 0 < : * , у ^ 1 9
для координат (х , у) точек которой справедливы неравенства
1.18. Показать, что в этом случае вероятность определяется
дробью, числитель и знаменатель которой отличаются от числи
теля и знаменателя соответствующей дроби для выборки с возвра
щением множителями вида 1+ о ( 1).
1.19. Разность X 2— Y 2 делится на 2 тогда и только тогда,
когда четность X и К одинакова; X 2— К2 делится на 3 тогда и
только тогда, когда X и Y одновременно либо делятся, либо не
делятся на 3.
1.20. При * = 2, 3, 5 имеем
{ X 4— Y 4 == 0 (mod *)} = {Х , К
0 (m o d * )}U {X ,
1.21. Вывести из теоремы Ферма, что
0 (m od *)}.
{Х Р -* — У * - 1 в 0 (mod р)} =
= {Х, К ее0 (m odp)}U {X, Y = £ 0 (mod/?)}.
136
137.
1.22.Чтобы получить явные формулы для указанных в усло
вии вероятностей, воспользоваться соотношениями
{ Х 3+ К8 *=ее 0 (mod 3)} = {Х , К = 0 (m od 3 )}U
U { X ^ 1, Y е — 1 (mod 3)} U {X = — 1, Y =
{X 3+ K 3 S о (mod 7)} = { X , Y ^ O (m od7 )}U
1 (mod 3)},
U{Х £ М Ъ К £М 2} и { Х € М 2, Y £ M %),
где A fi— множество всех чисел вида 7 6 + 1 , 7 6 + 2 , 76 + 4, М 2—
множество всех чисел вида 76 + 3, 76 + 5, 76 + 6 . Для доказатель
ства неравенства при п > 7 воспользоваться тем, что а2/4 — 1 ^
^ uv ^ а 2/4 при u-\-v = a, |и — и |^ 2. При
неравен
ство проверяется непосредственно с помощью явных формул.
1.23. Подсчет числа случаев, приводящих к событию Л1П Л 2=
= 0 , надо производить последовательно, фиксируя сначала число
элементов |
|= 6, а затем суммируя полученные результаты по
6 от 0 до N.
1.24. Согласно задаче 1.23 искомая вероятность при г = 2
равна (3 /4 )^ . Далее надо действовать по индукции по г. Подсчет
числа элементарных событий, входящих в рассматриваемое собы
тие, надо производить, предполагая сначала, что |Л1 |= 6, и поль
зуясь индукционным предположением, а затем суммируя получен
ные результаты по 6.
1.25. Разбить указанное в условии задачи событие на непересекающиеся события по значениям разностей g3— £i = £2— £з и
Чз — “Пг = Пг — Лз1.27.
Будем считать, что номер билета случайно взят
1000000 номеров, начиная с 000 000 и кончая 999 999. Тогда
искомая
вероятность равна
10~ 6*(6§ + 6? + . . . + 627)» где bk
(6 = 0, 1, . . . , 27) — число
всех чисел вида 102а2 + 10ai + a0
с 0
^ 9 , для которых йо + ^ + я ^ б . Показать, что
27
со
1.28. Пусть событие Л/ = {7-й билет счастливый}. Так как при
п < 9 события А{ попарно несовместны, то вероятность события
п
А=
U Л /={им еется хотя бы один счастливый билет} равна Р (Л )=
п
=
(Показать, что при п ^ 9 события А г и Л9 уже сов
местны.) Нетрудно видеть, что вероятность Р (Л/) отличается от
вероятности в задаче 1.27 весьма незначительно, так как Р ( Л /) =
10е— л + 1
где 6 ,- = 1э если х = 1 или
и
137
из
138.
6i — 2, если 1 < i < n (номер i-то билета не может равняться000 000 при i > 1 и 999 999 при i < я).
1.30.
2) Найти вероятность противоположного события
состоящего в том, что хотя бы один номер не появился. Событие А
представить в виде А = А г-\-. . . -\ -А ^ , где Аь (& = 1 , . . . , N) —
событие, состоящее в том, что шар с номером k не появился.
1.33. Воспользоваться равенством
Р {x{l < X i z < . . . < Xik + 1 } = Р {*! <
Л,
< ... < Xk + 1 \
при любых попарно различных i lt i2, . . . , i k + 2, . . . , 6 + 1}.
1.34. Найти вероятность противоположного события, состоя
щего в том, что в отобранных папках содержится целиком либо
две рукописи, либо ровно одна.
1.35. В условии не указаны числа женщин и мужчин среди
гостей. Задача имеет тривиальное решение, если эти числа не равны
друг другу. Если же в гостях находятся п женщин и п мужчин,
то для подсчета искомой вероятности можно воспользоваться фор
мулой Р (Л + £ ) = Р (Л) + Р {В) — Р (ЛВ), где Л = {«пары» занимают
места (1, 2), (3, 4), . . . (2п — 1, 2п)} (при некоторой нумерации
мест по кругу), В = («пары» занимают места (2 ,3 ), (4, 5), . . . ,
(2я — 2 , 2п— 1), (2п, 1)}.
1.36. Шесть номеров, вышедших в тираж, выбираются без воз
вращения из 49 номеров. Предположим, что все возможные ше
стерки номеров равновероятны. Если на данной карточке ровно 3
номера совпадут с номерами, вышедшими в тираж, то по данной
карточке игрок получит минимальный выигрыш. Найти вероят
ность события Л/j, состоящего в том, что на каждой карточке
угадано ровно 3 номера, причем £ = 0 , 1, 2 , 3 из них являются
общими для двух карточек.
1.37. 3) Рассмотреть заполнения двух типов: а) в одной из
ячеек нет частиц, в двух ячейках — по две частицы и в ( N — 3)
ячейках — по одной; б) в одной из ячеек нет частиц; в одной —
три частицы и в ( N — 2) ячейках— по одной частице.
4) Найти вероятность противоположного события.
1.38. Пусть Л/ — событие, состоящее в том, что i -я ячейка
осталась пустой. Найти Р (Лх-{- Л2+ . . . + Лдг).
1.39. Рассмотреть расположение М + п — 1 символов: п частиц
и N — 1 «перегородок». Найденное отсюда число расположений
совпадает, очевидно, с числом представлений числа п в виде
/г = г 1 + /'2+ . • .+ riV, где все
— целые числа.
1)
Событие fx0 = 0 происходит тогда и только тогда, когда все
/■£^5 1. Число наборов (гъ . . . , rN ), удовлетворяющих этому
условию, равно числу представлений числа п — N в виде п — N =
=
138
1 ) + . 1 ) »
гДе гк— 1 ^ 0 .
139.
2) Фиксировать пустую ячейку, а в остальных разместитьчастицы, как в 1).
1.40. а) Число таких вариантов размещения я человек в ряду
из N кресел, когда никакие 2 человека не сидят рядом, есть про
изведение я! и числа решений уравнения л;0+ * 1+ . . . + х п =
= N — я + 2 в целых положительных числах
— расстояния меж
ду занятыми креслами, O ^ i ^ n ) . Последнее число есть С % - п+1.
См. указания к задаче 1.39.
б) Каждый человек имеет ровно одного соседа тогда и только
тогда, когда все сидят парами, изолированными одна от другой.
Поэтому при нечетном я искомая вероятность равна 0 . При чет
ном я рассуждать аналогично п. а).
в) Если D U' дг— число таких способов размещения я человек
в ряду из N кресел, когда выполняется условие в), то при чет
ном N число D nt х равно произведению 2п и числа размещений я
человек в N /2 креслах. При нечетном N
&п, N = Dn, ЛГ-1 + nDn- i , N - 1*
1.41. Использовать указания к задаче 1.40.
1.44. Пусть Л /— событие состоящее в том, что в выбранной
подстановке i — > i. Найти Р (Лх + Л2 + . . .
1.45. а) Найти число подстановок в классе [1а *2аг . . . яа "].
б) Если исключить единичный цикл i — э- i , то получится под
становка из множества [\а1~ 12а* . . . (я — I)00'2-1].
в) Показать, что события i — ^ / ( / = 1 , 2, . . . , я, i Ф j ) рав
новероятны.
1.46. Использовать равенства
{% < * } = {£ < * } П { 1— I < 4>
(Ча > 4 = {1 > *}П{1 — I > *}>
где \ — координата точки Л.
1.50. Проверить, что геометрическое место точек, расположен
ных ближе к границе многоугольника, чем к его диагоналям,
состоит из равнобедренных треугольников, построенных на сторо
нах многоугольника как на основаниях и имеющих при основании
углы л /( 2я).
1.51. Установить зависимость числа корней от значений мно
гочлена в точках максимума и минимума.
1.52. Центр монеты можно считать равномерно распределен
ным в том ^-угольнике, в который он попал. Монета не заденет
границу ^-угольника, если центр будет отдален от нее на расстоя
ние, большее г.
139
140.
1. 53. Монета падает гербом вверх, если вектор нормали расположен выше горизонтальной плоскости.
1.54. Пусть (р, ф) — полярные координаты середины хорды.
Выразить | через R и р.
1.59. Интересующее нас событие описывается подмножеством
А = {(и, и): min (и,
1.60. Слова «случайно бросается» здесь естественно понимать
как случайную равномерно распределенную ориентацию цилиндра
относительно вертикального направления. Так как цилиндр одно
родный, то центр описанного вокруг него шара совпадает с его
центром тяжести. Цилиндр упадет на боковую поверхность, если
вертикальный направленный вниз луч пересечет боковую поверх
ность. Соогветствующая вероятность находится как отношение
площади сферического пояса описанной около цилиндра сферы,
ограничивающего боковую поверхность цилиндра, к площади всей
сферы.
1.61. (См. указание к задаче 1.60.) Вероятность того, что
цилиндр упадет на какое-то основание, пропорциональна телес
ному углу, под которым это основание видно из центра тяжести.
1.62. (См. указания к задачам 1.60, 1.61.) Центр тяжести
конуса расположен на его высоте на расстоянии 6 /4 от основания.
1.63. (См.
указания к задачам 1.60, 1.61.) Найти центр тя
жести полушара и определить величину телесного угла, под кото
рым видна плоская часть границы полушара из центра тяжести.
1.64. Положение бруса определяется положением прямоуголь
ника в плоском сечении, перпендикулярном оси бруса. Брус упа
дет на ту грань, которую пересечет направленный по вертикали
ъниз луч из центра тяжести прямоугольника. Ср. с задачами
1.60, 1.61.
1.65. Если А находится между Sk и Sfc+i» то расстояние от 0
до сторон Д ABC находится в интервале (6/2, ( 6 + 1 )/2), т. е.
Д ABC содержит внутри себя окружности S{ с 1С i < :[6 /2 ],
находится внутри окружности 5 /, 6 + 1
и граница Д Л Я С
пересекает окружности S / с [6/ 2] < i < 6.
Глава 2
2.3. Вероятность выбора любой заданной карточки равна 0,01.
2.6. Использовать определение условной вероятности и ре
зультат задачи 1.23.
2.7. Пусть событие Л/ состоит в том, что i-й (i = l, 2) студент
возьмет «хороший» билет. Положить Й = {Л 1Л2, А гА г, А гА г, А±АЪ},
р (Лх) = V 5, Р (Л2 1 Л^ = 4/ 24, Р (Л2 |А г) = 20/ 24. Отсюда однозначно
определяются вероятности элементарных событий.
140
141.
2.8* а) Пусть событие С,- = {появление белого шара в i-u испытании} (испытания с нечетными номерами относятся к игроку,
начавшему игру); событие А = {выигрыш игрока, начавшего игру}.
Воспользоваться равенствами А = С 1-\-С1С2С 31 А = С 1С2-ЬС1С2С3С4.
б, в) Решение аналогично а).
2.9. Пусть Do0 ( D i ° ) — событие, состоящее в том, что i-й шар
черный (белый). Воспользовавшись формулой (2.3), показать, что
все события
i = 1, .
.
с г1-\-г2+ . . . + £/v= М (ег*= 0, 1;
N) равновероятны. Поэтому
Р (Л^) = Р (Лх), Р (Bkt j) —
= Р (В 1>2), Р (Ck, г) = Р (С], 2)- Воспользоваться равенствами Blt 2 ==
= D ^ D (i \ C u2 = D (0l,D[2).
2.10. Цепочками из букв к, ч, б будем обозначать появление
красного, черного, белого шаров в испытаниях, соответствующих
месту буквы в цепочке. Например, событие кчч = {в 1-м испыта
нии появился красный шар, во 2-м— черный, в 3-м — черный}.
Использовать равенства
А х = б + ччб + ччччб,
А 2 = чб + чччб + чччччб,
В = к + чк + ччк + чччк+ ччччк + чччччк.
2.15. Использовать равенство ЛВ + АВ = А.
2.17. Пусть (£х, . . . ,
1) — координаты точки, равномерно
распределенной в (п — 1)-мерном кубе {(* ь . . . , x „ - i ) :
1= 1,
п}. Рассмотреть события
=
i = 1, 2,
п—1, 4 =
П (И !)< °
I /= 1
2.18. При п = 3 попытаться так приписать
вероятности 8 со
бытиям А гА 2А 3, ЛХЛ2Лз, . . . , ЛхЛгЛз, чтобы условия задачи
выполнялись, но события Лх и Л3 не были бы независимыми.
2.19. Рассмотреть совокупность событий / П
1 (» = 1,
8( = 0 или
А )} , где А Т = А {, А ^ = А[.
2.20. Сопоставить каждому событию Л /С {1 , 2, . . . , я} = Й
вектор
у которого / - я ( / = 1,
п) координата равна 0
(если /(£ л ,-) или Y'p J (если
Л/). Переходя к векторам 61, . . .
. . . . bh $ R b :
6/ = ((0 /, fli), (а/, <22), . . . , (fl/, д&))>
показать, что если события А 19 . . . , Л* попарно независимы, то
векторы д19 . . . , a , b£ Rn линейно независимы.
141
142.
2.21. Пусть Л / = (изделие прошло i-ю проверку}, i — 1, 2.По условию задачи события Лх и Л2 независимы в обоих случаях.
2 .22.
б) Воспользоваться
неравенством Р ( Л ^ ) ^ Р ( А г) +
+ Р (Л 2), где А г и Л2— события, состоящие в том, что 1-й и 2-й
приборы будут работать.
2.23. Участник лотереи получает минимальный выигрыш,
если он угадал ровно 3 номера, и какой-либо выигрыш, если число
угаданных им номеров не меньше 3. Положим Л^ = {/г-й участник
получает минимальный выигрыш}, B k = {k-ft участник получает
какой-либо выигрыш}, k = \ , 2. Найти Р (Лй), Р (Bk), k = l, 2.
2.24. Положим Л^> = ( 6-й элемент не вышел из строя}, Л(*> =
*= (&-й элемент вышел из строя}, k = l, 2, . . . , 5. По условию
задачи события любого набора, составленного из событий Л<*>,
Л<^>, & = 1, . . . , 5, с попарно различными индексами, являются
взаимно независимыми. Обозначим В событие, состоящее в том,
что по участку, содержащему элементы A lt Л2, Л8, может прохо
дить ток. Воспользоваться равенствами
В = (Л<!> + Л(2>) Л<4>= Л <XM (4>+ Л ^ Л (2М<4>,
С = Л(5>Л<3>+ Л ^ Л ^ В .
Заметим, что для вычисления вероятности Р (В) непосредственно
использовать равенство В = Л^М^4)+ ^ (2)Л(4) нельзя, так как
Л(1)Л<4> и Л(2>Л(4> не являются несовместными событиями.
2.25. Положим
Ло° = {при
i -м выстреле
допущен
промах},
Л(11) = {при i -м выстреле происходит попадание}. По условию за
дачи события Л£>, Л<*>,
...,
Л^л)
(е/ = 0 ,
1;
£ = 1,
. . . , я)
взаимно независимы. Найти вероятность того, что было меньше
двух попаданий.
2.27. Пусть С = (изделие, поступившее на проверку, удовлет
воряет
стандарту}.
В
задаче
2.21
вычислены вероятности
Р { А гА 2 |С }, Р (Л ХЛ2 |С}, где Лх = (изделие прошло первую про
верку}, Л2 = (изделие прошло вторую проверку}.
2.28. в) Использовать равенства
М
( М — т) С% = М С м -1,
2
т-О
c m - i Cn ~™
m =
Cn - ъ
2.30.
Введем события С = (перелить кровь можно}, Л/ = (до
нор имеет i -ю группу крови}, В; = (больной имеет i -ю группу
крови}. Найти Р (Л /), Р (В /), Р (С |В/) в предположении, что
группы крови донора и больного независимы и распределены
согласно приведенной в задаче статистике.
142
143.
2.31. Положим С = {вибрация},В = {перегрев}. Найти веро
ятности событий СВ, СВ у СВ, СВ,
2.32. Используем те же обозначения, что в указаниях к задаче
2.31. Положим Р (ВС) = х . Найти вероятности событий ВС, ВС, ВС
как
функции от х, Р (В),
Р (С).
Показать, что
s=^min (Р (В), Р (С)).
2.33. Положим А = {случайно выбранная урна содержит 2 бе
лых и 3 черных шара}, В = {случайно выбранная урна содержит
1 белый и 1 черный шар}, С = {из выбранной урны извлечен бе
лый шар}. Используя условие задачи, определить вероятности
Р (А ), Р (В), Р (С | А), Р (С |В).
2.35.
Введем следующие обозначения событий: А = {передана
последовательность А А А А }, В = {передана последовательность
ВВВВ}, С = {передана последовательность СССС}, D = {принято
ЛВС А ). Так как при приеме ABC А вместо А А А А буква А была
1
1
искажена два раза, то нужно положить Р {D |А ] = а — ^---------— а.
„
Аналогично определяются вероятности
пользоваться формулой Байеса.
—а —а
Р {D |В }, Р {D |С}. В ос
2.38. Пусть A k )— событие, состоящее в том, что t-й игрок
(i = 1, 2) извлек k белых шаров. Из условия задачи естественно
определяются
вероятности
Р {Ajj^} (& = 0,
1,
2),
Р{Ak}\А^}
(k = Q, 1; 1= 0, 1, 2). Найти ? { А ^ \ А ^ } 9 k = 0, 1, 2.
2.39. Найти вероятность противоположного события.
2.43. Искомую вероятность можно найти, используя то, что
для любого элемента x £ S
Р { х ^ А хА 2} = 1 - Р { x £ A i A z} = 1 — Р { х £ A J Р { х £ А 2}
и что отбор разных элементов в множества А / происходит неза
висимо.
2.44. Множества Ац . . . , А г попарно не пересекаются, если
каждый элемент x £ S либо не включается ни в одно из г мно
жеств, либо включается ровно в одно множество.
2.45. Решать так же, как и задачу 2.44.
2.46. а) Каждый элемент x £ S независимо
от
остальных
г
включается в
~
П А / с вероятностью р г, б) Воспользоваться co
ir: 1
г__
отношением
у А{ = П
и свести задачу к п. а).
i= 1
i= 1
2.47. Моделью исследуемого явления можно считать схему
Бернулли. Обозначим через А\ событие, состоящее в том, что
в момент t по дороге мимо пешехода проезжает машина, / = 1,
143
144.
2, 3, . . . События А ъ А 2, . . . независимы, Р (Af) = p, Р (Л*) == 1 — p = q. Выразить интересующие нас события через At, Л2, . ..
Например:
{пешеход ожидает 4 с .} = Л1Л2Л3Л4Л5ЛвЛ7;
использовать взаимную независимость событий.
2.48. Результативные партии рассматривать как испытания
Бернулли с одинаковыми вероятностями исходов.
2.49. Последовательно обрабатываемые детали по принадлеж
ности к 1-й или 2-й группе образуют симметричную схему Бер
нулли. Событие, вероятность которого мы ищем, можно за
писать в виде А т ГП С - { - В т г П С, где Лт> г = {из r + т пер
вых деталей в 1-ю емкость попало г деталей, а во 2-ю попало т
деталей}, В
г = {из г / п первых деталей во 2-ю емкость попало
г деталей, а в 1-ю попало т деталей}, С = {(r + m + 1)-я деталь
попала в 1-ю емкость}. Предлагаемая задача является перефор
мулировкой известной задачи Банаха (см. [11]).
2.51. Воспользоваться теоремой М уавра— Лапласа.
2.52. Воспользоваться предельной теоремой Пуассона.
2.53. Использовать теорему Пуассона.
2.54. При решении п. б) вывести равенство
Р {1 Ь «-т | < * } =
а затем применить уточненную формулу Стирлинга для вычисле
ния 2 ~ 2тС1
2т2.56. Использовать теорему
М уавра— Лапласа. В ответе
оставить знаки, не меняющиеся при изменении границ 940, 1060
на ± 1. (См. введение к гл. 2, а также задачи 2.54, 2.55.)
2.57. Пусть v — порядковый номер 1025-го числа, делящегося
на 3, \in— число чисел, делящихся на 3, среди первых п чисел
таблицы. Использовать равенство
Р ( v ^ 2 500} = P {[а 2499 < 1025}.
В ответе сохранить разумное число знаков. (См. указание к за
даче 2.56.)
2.58.
а) Пусть в гардеробах по х мест; обозначим через ^
число пар, выбравших гардероб одного входа; тогда 500— jjl —
число пар, выбравших другой гардероб. Используя теорему
144
145.
Муавра— Лапласа, подобрать х так, чтобыР {2|х < х ,
1000— 2[х < я} « 0,99.
2.59. Воспользоваться схемой Бернулли с /1 = 2500, р = в/ 8о =
= 0,2, <?= 0,8.
2.60. Рассмотреть все цепочки исходов длины /, содержащие
k успехов, из которых один стоит на конце цепочки.
2.61. Воспользоваться схемой Бернулли, в которой испыта
нием является бросание двух костей; за два исхода каждого
испытания принять выпадение или невыпадение хотя бы одной «6».
Рассматриваемая схема является частным случаем (2.15)— (2.17).
2.62. Занумеруем подряд бросания монеты. Бросания с не
четными номерами производятся первым игроком; остальные —
вторым. Пусть Ci — событие, состоящее в том, что в i-м бросании
выпал «герб».
а) Событие, состоящее в том, что игра закончится до 4-го
бросания, представляется в виде С1-\-С1С2-{-С1С2С3.
б), в) рассматриваются аналогично.
2.63. Вероятностное пространство определяется формулами
(2.15)— (2.17) с N = 2, р\ = р, р2 — Я* Обозначим рассматриваемое
событие А. Положим Б^ = {нуль впервые появился при k -м исоо
пыгании}. Тогда
Р (А) = 2 Р
k= 1
2.64. (См. указание к задаче 2.63.) Нетрудно установить, что
рассматриваемое событие может произойти лишь в том случае,
когда первые два испытания приводят к двум нулям.
2.65. Обозначим рассматриваемое событие А . Исход i - го ис
пытания (0 или 1) обозначим Н/. Для условных вероятностей
Ро = р [ A I Si = ° } .
Pi = p М
l£ i= l}»
Р п = Р {Л |Si52 = 1}
мож но,
пользуясь формулой полной вероятности, составить систему ли
нейных уравнений. Решив ее, находим Р 00 |ш = Р { A } = zCIP o+ P P v
При составлении системы использовать равенства вида
р {Л U i = 0, g2= 1} = Р {Л |g1= l} = Pl,
Р{Л|Ь = 1, ?2= 0} = Р {Л |g1= 0} = p0, ...
2 .66. Число единиц в п испытаниях схемы Бернулли одно
значно определяет положение частицы.
2.69.
Найти вероятность противоположного события. Непра
вильная передача происходит в следующих случаях: А = {иска
жено не менее 4 знаков}, £ = {два знака принято правильно,
а остальные знаки одинаковы}, С = {два знака принято правильно;
среди остальных ровно два одинаковых; из двух пар частых зна
ков выбирается пара неверно принятых знаков}.
145
146.
2.70, Возможны два подхода.1) Воспользоваться формулами
п\
(п = т1+ . . . + m N ),
X
( * + . . . + a * )'=
st + . . . + s k = s
2)
Положим B iy) = {B
появился
исход
B q}) — {в /-м испытании не появился исход 1}. Тогда события
,
B < J ( e y = o . 1)
в£>,
/-м
взаимно
испытании
независимы и
Р{В<Л} = Ръ
Р {^0У)} = Р2+ •••-\~PN = l —Pi2.71. Использовать решение задачи 2.70.
2.72. Решается аналогично 2.70.
2.73. Положим A i ~ { i - я ячейка осталась пустой}. Тогда
(М "» N )= k } =
=
U
(Л { А{
i < h < ...< ik < N [ h 12
Ч
. . . Л- П
lb
П
/e fi,
ф ь, у
Л,-
Из решения задачи 2.72 следует, что
(
П
Р </6Д1
т
•••»
~AJ \Ai . . . A i
1
1
\
1
совпадает с вероятностью того, что после размещения п частиц
по N — k ячейкам, отличным от il9 . . . ,
среди этих ячеек нет
пустых. Воспользоваться решением задачи 1.38.
2.74. Обозначим 0 „ число очков, выпавшее при п-м бросании;
v — номер последнего бросания. Положим 4 « = { 0 W^ 5 } , Вп =
= { 2 « ^ 0 „ < 5}. Возможны два подхода к решению.
1) Событие С, вероятность которого требуется найти, можно
оо
представить в виде С = В Х+
U
. . A n_ xB n.
п= 2
2) Доказать равенства
Р {С } = Р { В 1} + Р {Л 1} Р { С | Л 1},
PfC H ^pjcj.
2.75. Найти вероятность того, что в k-u тройке все исходы
различны. См. указания к задаче 2.74.
2.76. См. указания к задаче 2.74.
146
1},
147.
2.77.Обозначим через А ( появление хотя бы одной «6»
у игрока А при i-м бросании; аналогично определяем В{ для
игрока В . Можно воспользоваться любым из подходов, описан
ных в указаниях к задаче 2.74.
Глава
3
3.4. Угол между положительным направлением оси ординат
и лучом АВ имеет равномерное распределение на отрезке [0, 2л].
3.5. Показать, что {F (£) ^ а:} = {^ « ^ 7 7_ 1 (*)} для любого
х,
и { F _ i (г|) ^ x} = { r \ ^ F (х)} для любого х, — оо <
< X < 00.
3.6. Распределение величины rj = g (£ ) будет иметь атом в точ
ке у, т. е. Р (т) = у) > 0, если, например, уравнению g ( x ) = y удовлетворяют все точки интервала Xi<^ х
х2 и вероятность собы
тия
положительна.
3.7. Воспользоваться тем, что при достаточно больших N зна
чения F (— N) и 1— F (N) могут быть сделаны как угодно малыми,
а на любом замкнутом интервале [— N, N] непрерывная функция
равномерно непрерывна.
3.11. Найти сначала функции распределения, рассматривая
пару (g, г]) как случайную точку, равномерно распределенную
в квадрате со стороной а, и вычисляя площади соответствующих
фигур.
3.12. Воспользоваться тем, что двумерная плотность распре
деления
г] равна е - х - У , х ^ О , у ^ О . Вычислить сначала функ
цию распределения.
3.14. Воспользоваться формулой композиции (3.3). Учесть,
что плотности /?£ (х), рх\ {у) на разных интервалах определяются
разными аналитическими выражениями.
3.15. См. указания к задаче 3.14.
3.16. Показать, что при любом f £ [ 0 , а]
t2-\-2t ( а — О
аР {min (g,,
3.19. Найти сначала функцию распределения г].
3.20. Найти
p { t i < * } = p { ( 6i, . . . . Ъп)£Вх },
где
£ * =
{(« И
• • •*
и п): Иг /( И 1 +
. . . +
Un) S ^ * } .
147
148.
8 .22.Воспользоваться равенством
{ i i + i 2 < * } = {S2 < * , 8i = 0 ) U { 6 . < * - 1 . 6 х = 1 }
и независимостью случайных величин.
3.24. Показать, что
Р П= Р { S i + ёз— четное число}.
8.27. Пусть
— число очков, выпавших в s-м испытании.
Выразить событие (0 = /, v = n) через события, связанные со слу
чайными величинами
s = 1, 2, . . .
3.28. а) Найти
Р (0J. = г, т 2 = /2, 02 = /» т 8 = / 8, 03 = £).
б), в) Найти совместное распределение
(0!, . . ., 0ДГ, Ti, . . ., Т//).
3.29. См. указание к задаче 3.28.
3.30. а), б) Использовать равенства
{l^ k ^ A p A ?
. . . А Ы к+ и ,
{ l 1= k, |, = /} = у С . . . А р А ^ ' А ? ™
... A0
( k+l+1)Aik + l+ i\
где
Aofe) = {£-ft шар черный},
= { k -и шар белый}.
в)
Событие (g i = ^i, §2 = ^2» •••» ? m + i = ^ M + i} однозначно оп
ределяет моменты появлений белых и черных шаров.
3.32.
Оценить вероятность Р (£ = т]) сверху суммой
?{\ 1 \ > N , h i >ЛГ} +
и показать, что при достаточно больших целых N и п эта сумма
может быть сделана как угодно малой.
3.34. Показать, что g и т] равномерно распределены на [0, 1]
и Р (| = Г]) = 1.
3.35. Рассмотреть распределение двумерной случайной вели
чины (|, г]): Р (| = 0, n = l ) = P ( g = l , Л= 0) = 1/2.
3.36. Пусть действительная случайная величина £ имеет плот
ность. Рассмотреть двумерную случайную величину (£, г\) с £ = £>
*)=£
3.37. Воспользоваться при a i « ^ a 2» Ьг ^ Ь 2 соотношением
г ] < М C { a i < £ < a 2} U{^i < г)<Ы14В
149.
3.38. Воспользоваться формулой композиции (3.4).3.39. а) Воспользоваться тем, что Р(тх = т 2) = 0 (см. зада
чу 3.32), а также тем, что т*— т2 и т 2— т х одинаково распределены.
б) Время ожидания 3-го клиента равно min (тх> т 2).
в) Событие, состоящее в том, что 3-й клиент закончит разго
вор раньше 2-го, можно записать в виде: Тт + Тд < т 2. Найти сна
чала плотность распределения Тх+Тд.
3.40. Пусть
— время разговора &-го посетителя. Вероят
ность P k того, что k-Pi посетитель закончит разговор первым, равна
Pk = Р (T'k ^ ^1» T'k ^ ^2» •••» T’k <
—1»
^ T'k+1» •••» T'fc < T-«)
Используя результат задачи 3.32, показать, что Р1= . . . = Р „ .
3.42. а) Использовать равносильность событий {£<d > х}
п
и П
£=1
{ £ / > х} и независимость
I f б) использовать равносильность
п
событий
{?(/;)
и П
зовать
равносильность
и независимость
t= 1
событий
{л:, <
в) исполь-
g(1)} f| {S(«> <
* 2}
и
п
П {xi < l i < ; x2] и независимость Е/.
i= i
3.43. Пусть Вт = (значения т — 1 величин из §1» . . . ,
по
пали в (— оо, х), одно значение— в [х, х + А х ) и п — т значений
в [х-\-Ах, + оо)}. Показать, что
р {(?</*)€ (*> * + А * ) ) \ 8 т } = О (Ал:) при Ах —*0.
Воспользоваться полиномиальной схемой.
3.44. Использовать равенства
< if. < ••• < ^ +1}= P t t i < h < ••
где (iv i2,
lk+ i) — любая перестановка ( 1, 2, . . . , £ + 1),
и учесть, что P (g l* = | y- ) = 0 при i Ф / (см. задачу 3.32).
3.45. Пусть Xi < yi < Xi + l < y i + i ( i = l, . . . , /г— 1). Найти
вероятность Р {* / <
£ = 1 , . . . , п). Разделив эту вероятп
ность на J J (y i— Х() и устремив yi к */, £ = 1, . . . , п, получаем
t = 1
искомую плотность.
3.46. Найти плотность совместного распределения Ах, . . . , Д „ ,
преобразовав найденную при решении задачи 3.45 плотность сов
местного распределения 1(1), . . . , 1{п).
3.47. Воспользоваться результатом задачи 3.46.
449
150.
3.48. Вывести из задачи 3.44, что Р ( А „ ) = п ~ к, п = 2,3,и воспользоваться неравенствами
п
3.49. Воспользоваться результатом п. б) задачи 3.17.
3.50. Выбрать любое вероятностное пространство, на котором
задана случайная величина tj, имеющая равномерное распределе
ние на отрезке [0 , 1], и воспользоваться задачей 3.5.
3.51. Показать, что Р {£ = | или £ = т]} = 1 и что поэтому
Далее заметить,
при U — Y
<
что случайные величины Zi и £г: £ i = £ , ?2 = т1
к\—
Si = г|» Ег = 6 в противном случае— удо-
влетворяют условиям Р {£ * = £} = Р {S/ = т]} = 1/2, / = 1, 2. Тем
самым все сводится к вычислению функций распределения слу
чайных величин
тах
3.52.
Использовать соотношения
P {S < r )} = P { g > r , } = T ,
P {m in (g , r | X S < m a x ( 6, т])} = 1
и указания к задаче 3.51.
3.53.
Заметить, что если ах = т\п{п: Р (Х = я } > 0 } Ьх =
= т а х { п : Р { Х = п } > 0} и аналогично определены ау и Ьу, то
а = ах-\-ау, b —bx-\-by. Вывести отсюда, что
m in {P (Z = a ), Р (Z = b)} s^m in {ху, (1 — jv) (1 — г/)},
где х = Р (Х = ах ), y = f> (Y = ау). Максимизировать правую часть
неравенства сначала по у (при фиксированном х)> а затем по х .
п -1
3.55. Предварительно доказать, что n ^ = ^ k 2
для
mz* 1
любых п,
150
где х ^ = х ( х — 1) . . . ( * — # + 1), а затем преоб-
151.
разовать правую часть равенстваМ |М = 2
п= 1
« И р {!= « }
3.56. Заметить, что если */ = Xi + x2+ •••, где все слагаемые
принимают только значения 0 и 1, то
ут =
2
хн - - - \
3.57. Использовать результат задачи 3.5 и геометрическое
истолкование интеграла.
3.58. Использовать равенство £ = т а х ( 0 , £ )— шах (0, — |)
и задачу 3.57.
3.59. Рассмотреть отдельно случаи а > 0 и а < 0. Найти функ
цию распределения
и воспользоваться задачей 3.57.
3.60. Использовать результат задачи 3.5.
3.62. Заметить, что Р *{r|i + r|2= l } = 1.
3.65. б) Выразить R n через e lt е2, . . .
3.67. Применить математическую индукцию.
3.68. Воспользоваться соотнош ением? {v > п} = Р {Si + £2+ " '
1} и результатами задач 3.54 и 3.67.
3.69. Использовать метод неопределенных множителей Ла
гранжа.
3.71.
Выписать явную формулу для D ( £ + t ]) и заметить, что
коэффициент корреляции р (£, rj) может принимать любые зна
чения в интервале [— 1, + 1 ] .
3.74. Воспользоваться формулой A = 2 ( i
£10Cl ••
где
а
/1
2 ... п \
).
V « i а 2 • • • « »/
3.75. Заметить, что если матрица А =[| а/у ||£ /= ъ то
сумма берется по всем подстановкам а =
i, /as 1
Воспользоваться тем, что М|?г = 0
для
любого
нечетного
tn <k.
3.76.
Представить М sin £ и М cos § в виде суммы интегралов
по [2л£, 2л (& +*)]> &= 0, 1, . . . , а затем показать, что каждый
из этих интегралов может быть представлен в виде интеграла по
(0, л /2) или по (0, л) от положительной функции.
151
152.
3.77. Установить равенство М - 3 ^ = 4 - + М I—п
2 '
л
р — 1! 2 воспользоваться неравенством М — — ~ I^
/г
При
р ^t 1/ 2,
например,
=
при
р > */2,
Л/ D — .
2 |
положить
г
I
п
— i - 1=
^и’ ГДе ^*= 1 ’ если
и 1п=0,
р
с помощью
если |х„ > /г — \х,п. Найти lim М 5„ =
lim
теоремы Муавра — Лапласа.
3.79. а) Положить Ak = {Uk- i = s ^ tik}>
и использовать разложение
{i'll= ei> •••» Ч к = Ч } =
в к= { h k -i= h k }
/
и
1< !!< ...< ik
и
б) Заметить, что {v = 2fe} = (^ 4ft+ Л|)
. . . В * _ 1.
3.80. См. указания к задаче 3.79.
3.81. а) Положить 0i = | i + . . . + Ъп, где | / = 1 , если i — м ,
= 0 в противном случае; тогда
п
02
i=
б)
п
2
if / = 1
Положить 02 = 1 у
=
i-1
g/y, где
i Ф']
|х/ = 1, если
i —*] —► и
1ф]
6/ / = 0 в остальных случаях.
в)
Написать для 6Г формулу, аналогичную случаям г = 1
и г = 2.
3.82. Пусть |х0— число непоявившихся номеров. Тогда (х0 =
= l i + £2+ •••+ I n > гДе l k — l> если
номер не появился,
и |ft = 0 в противном случае.
3.83. Представить g в виде суммы индикаторов | = 6х + ^2+ . . .
. . . + $«» где 8/ = 1, если i-й шар в выборке белый, и 6/ = 0
в остальных случаях (предполагается, что шары вынимаются из
урны поочередно). Воспользоваться тем, что
3.84. Показать, что случайные величины §х, . . . ,
опре“
деленные в задаче 3.30, одинаково распределены и что т / = £ /-{-1,
152
153.
1= 1, . . . , М 9 тд1 +1 = 5 ^ +1. Использовать равенство S i + § 2+ - « *•••+ SiW+i = N—
3.85. Воспользоваться равенством
fx0 (n,
N) = 0Х+ . . . + 0дг,
где 0/ = 1, если i-я ячейка пуста, и 0 / = 0 в противном случае.
3.86. Воспользоваться результатом задачи 3.85.
3.87. См. указания к задаче 3.85 и задачу 3.56.
3.88. Положить
fxr = 0ir) + . . . + 0w\ г д е 0 /г)= 1 ,
если
/-я
ячейка содержит ровно г частиц, и 0j.r) = 0 в противном случае.
См. далее указания к задаче 1.39.
3.89. Использовать равенство %Пг / = ех> / + . . . + 8и, Ь гДе
£kt/ = 1, если в 6-м испытании появился / - й исход, и &kj = 0
в противном случае.
3.90. См. указания к задачам 3.85 и 3.88. При решении п. в)
использовать выпуклость вниз функции х п.
3.91. Использовать равенство V£ = tx+ . . . + Т£, где T i = l ,
Ту=Vy— v y _ x (/ = 2, 3, . . . , iV), и результаты задачи 3.28.
3.92. Если 6/ — число пассажиров t-ro автобуса, которым не
досталось билетов, то
£=
+ ... +
3.93. Прибыль предприятия г\ представить в виде т] = £х+
+ ^2+ * * . + 1п» где l k— прибыль за 6-е изделие.
3.94. Положить T\k— £ife>+ •••+ &k)> гДе
— Ь если, на
i-й карточке 6-го игрока совпало 3 номера с номерами, выпав
шими в тираже,
= 0 в противном случае.
3.95. б) Использовать равенство 1тГг i = r\mt /, где %mt / — число
участников, угадавших ровно i номеров.
3.96. Представить § в виде суммы 01 + 02 + 03+ 04» гДе 0 / = 1»
если i-я вершина квадрата, в который попал центр круга, лежит
в круге.
оо
3.97. Представить |5 | в виде |S |=
2
/г =
a k* где а ^ = 1, если
— оо
6£ S , и
=
если 6 (£ S.
3.98. Определить на круге случайную функцию
1,
«'Но:
Тогда £ = ^ % ( г ,
если
Р£Ау
если
Р(£а .
ф) rdrdtpy где г, ф— полярные координаты
к
точки Р. В данном случае знаки математического ожидания и ин
153
154.
теграла можно поменять местами (см. [6], теорема Фубини), таккак и
*
|%(г, ф) |тdr сйр < оо.
К
3.99.
Пусть %т (х, у) = 1, если точка (х , у) покрыта ровно т
кругами, и %т (х, у) = 0 в остальных случаях. Тогда
%пг(х, y ) d x d y .
Воспользоваться тем, что
0 < ц га—
% m (x ,y )d x d y <
х 2+ у 2 < R - r
< зх ( R + г ) 2 — зх ( Я — г ) 2 = 4 к г Я
с вероятностью 1. По теореме Фубини
1т (*> у) d x d y =
x2+ y 2 ^ R - r
^
М хи (х, у) dx dy.
x2+ y 2 ^ R ~ r
Найти tA%m (x f у) и вычислить последний интеграл, переходя к
полярным координатам.
3.100.
Представить |х00 в виде суммы индикаторов г)а +
+ г|3+ . . . + 'Пи» где % = 1» если при k-м испытании появилась
цепочка НН, и т|^ = 0 в остальных случаях. При вычислении
главного члена асимптотики дисперсии необходимо использовать
не 1, а 2 первых члена асимптотических разложений (М|х0о)2
и Mjxoo*
3.102. Заметить, что /-е испытание является первым в серии
успехов тогда и только тогда, когда оно привело к успеху,
а ( / — 1)-е — к неудаче. Поэтому если 0 / = 1 , когда /-е испыта
ние является началом серии успехов, и 0у = О в противном случае,
то: 1) Tb = ei + e 2+ .. .+ 0 » ; 2) Щ = рд (/ > 1); 3) Р {0у0у+ 1= О }= 1 ;
0у и 0^ независимы при |/ — k \ ^ 2 . Далее см. указания к зада
че 3.100.
3.103. Пусть £k ( k = 1, 2, . . . , 10) — k-e по порядку извлечения
число. Доказать, что £* одинаково распределены.
3.104. Плотность распределения £(у> найдена в задаче 3.43.
Для интегралов, возникающих при вычислении моментов, получить
рекуррентные формулы с помощью интегрирования по частям.
3.105. Показать, что для вычисления М (£ а*) |\ф = х), 1
<
<
можно воспользоваться результатами задачи 3.104, так
как совместное условное распределение £(1), . . . , £ ( / - п при усло
вии Ё(у) = * совпадает с распределением яг^и, . . . , хг\ у -г), где
T ](i)^ . . .
— вариационный ряд, построенный по независи-
154
155.
мым случайным величинам rjlf . ..*распределение на отрезке [0 , 1].
3.106. При Mg = т Ф (0, 0 .........
величину (|, ет ), где ет =
1(5. вя )| < | Е | ,
имеющим равномерное
0)
рассмотреть случайную
[ m |" > и заметить> что
[M (g , ет) |= |m |.
3.107. Рассмотреть векторную случайную
величину £' =
=
Л) € # 2 и воспользоваться результатом задачи 3.106 и ра
венством |£ |= |£' |.
3.108. Выразить D (gi + . . . + g„) через С и воспользоваться
неотрицательностью дисперсии.
3.109. Воспользоваться неравенством
г { П ] > х } ),
где 1А — индикатор событий А ( I А = 1, если А происходит, I д = 0
в противном случае). Показать, что М (| g \kJ^ 11 ^
— ^0 при
х —> оо.
3.110. Воспользоваться тем, что 'П1+ т]2+ . . . + ТЬ = 1 и рас
пределения rjlf . . . , г]п одинаковы. Распределения пар rj,*, r]y (i ф /)
также одинаковы.
3.111. Найти производную по х функции cp(x) = M |g — х \ 9
где х — координата точки В.
3.112. Воспользоваться решением задачи 3.111.
3.113. Воспользоваться равенством
М (g - х)2 = М (g - Mg)2 + (х - M g)2.
3.114. Пусть P { a ^ g ^ f r } = l , & — а = 1 . Воспользоваться тем,
что D gs^ M ^ g —
(с м- задачу 3.113).
3.115. Воспользоваться тем, что при a i ^ b i
{ai ^
^
^ i} П { az ^
Лг ^
^ 2} П {^1 +
а2^ Л1“Ь Л2 ^ ^1 + ^2}*
3.116. Воспользоваться задачами 3.114, 3.115 и доказать, что
из предположения о том, что g сосредоточена на отрезке длины
I < оо, и из безграничной делимости распределения g следует ра
венство Dg = 0, т. е. вырожденность распределения g.
3.117. Рассмотреть независимые точки X lf . . . , Х 6 £ R 2, имею
щие распределение Р. Показать, что если х 6— число треугольни
ков X/XyXfe, l s ^ i < j < & < ; 6, имеющих хотя бы один угол не
меньше 120°, то: а) М х6 = СвР3; б) Р { х 6^ 1} = 1, т. е. М хб ^ 1.
Доказательство п. б) сводится к рассмотрению двух случаев:
155
156.
1) точки Х г,Х в образуют выпуклый б-угольник, 2) одна из
точек находится внутри треугольника, образованного какими-то
тремя другими.
3.118.
Рассмотреть совокупность Х ъ Х 2, Х 3, Х 4, Х 5 неза
висимых случайных точек R 2, имеющих распределение Р. По
казать, что если к 5— число
выпуклых четырехугольников,
образованных
точками
X /,
i = 1,
5, то: а) М х5= 5Р4,
б) Р {и 5^ 1} = 1, и поэтому
М х5 ^ 1. При доказательстве
б) использовать рис. 3.
3.119. Воспользоваться тем,
что выпуклая вниз функция f (х)
удовлетворяет неравенству
/ (х) Ss / (л-0) + С Хо ( х — х а),
— 00 < X < 00,
где lim / ' (л:) ^ СХо ^
х\х0
3.120. Использовать выпуклость
(r ^ s 1) и задачу 3.119.
вниз
lim / ' (л:).
х\х0
функции f ( x ) = \x\r
3.121. При доказательстве первого неравенства показать,
что можно ограничиться случаем О ^ у ^ х и что при
производная по у разности правой и левой частей неотрицательна.
Далее заметить, что при указанных в формулировке задачи усло
виях распределения случайных величин £ + Л и £ — Л совпадают,
и поэтому
M | i + r i | '- = y ( M | i + r i | '' + M | g — Т)| О-
3.122. Применить
3 . 121.
3.123.
метод математической индукции и задачу
Использовать задачу 3.119 и равенство
М | Е + г | Г = М (М { | 5 + л Г Ш ) .
3.124. Показать, что если S* = i i + . . . +
чина
и случайная вели
не зависит от 5^, %k+t и распределена так же, как
l k + v то распределение
— 5ft+i симметрично и
М [ Sk + i |' < М |S * + Е* +1 - Й +1 |', < M | S ft|r + 2 rM |5ft+1|'\
3.125. Утверждение п. а) следует из утверждения п. б), а
это последнее следует из линейности операции cov (£, £) по каж
дой из переменных.
156
157.
3.126. а) Показать, что (a, Bd) = X>{at |).б) Воспользоваться тем, что условие {ранг В не больше г )
эквивалентно условию (существуют линейно независимые векторы
blt . . . , &£-г» для которых B b i = 0 } , условие (Dr] = 0} — условию
{P{rj = C} = 1 для некоторого С }, а также п. б) задачи 3.125.
А п,
3.127. Вводя индикаторы Хг» •••» Хи событий А ъ
установить равенство
пр =
M(xi + ... + X » )= S Р
2
Л=1
k
/г = 1
(Р
и вывести из него, что для любого т = 1, 2, . . . , п
т? { В т} < п р < т — 1 + (n — т + \ ) Р { В т}.
3.128. а)
Рассмотреть
случайные
величины
£s=l
и
Т|:
Р (г|= 0) = 1 — р, Р (г| = 10/р) = р, р € (0, 1].
б) Рассмотреть случайные величины | и т], имеющие равно
мерное распределение на [0, 1] и такие, что Л = { 5+ Р } » т * е* Л
равно дробной части числа £ + р.
в) Показать, что
при а < 1. Рассмотреть слу
чай, когда
I = {р + ч М Случай а > 1 сводится к а < 1 делением на а:
Р (Н < т ]) = 1— Р {т]/а < 1/а}.
3.129. Вычислить
М | £ — 1/2 | и
М|т] — 1/2 | и воспользо
ваться неравенством \х—
*1 + 1#1
3.130. Показать, что случайные величины min (£, ri) и шах (£, т|)
удовлетворяют условиям задачи и что
Р {min (g, r i X C < n i a x ( 6, П)} = 1.
3.131. Показать, что если
f - i («/) = sup [х: F ( x ) ^ y }
и
{ % = l } = { g ^ i 7_ 1 (1 — а)} = А,
то для любой другой случайной величины
P { x ' = l } = af
Р {х ' = 0} = 1— а и {%' = 1} — А ' ф А , справедливо неравенство
так как
М (I шах (х — Х'> °)) ^ F - i ( 1 — «) р М \ Л ') .
M (£ m a x (х ' — X» O K F - j (1 — а) Р ( Л \ Л )
и
Р(Л'\Л) = Р(>4\>4').
157
158.
Минимальное значениеМ (|%)
достигается
при
{% = 1} =
=
F _ i (а)}. Для вычисления экстремальных значений М(|%)
воспользоваться задачами 3.57 и 3.58.
3.132. Представить £ в виде £ = ri-l-(E— г\)%, где случайная
величина % принимает значения 0 и 1 и
= 0} = {g = т]}, { / 1= 1} =
= {£ = £}. Далее воспользоваться аддитивностью математического
ожидания и результатом задачи 3.131 (предварительно вычислив
плотность распределения Е— rj).
3.133. а), б), в) Найти Р (g = ri); использовать равенство
Р(Е> Л)=Р(Е< Л>3.134. а), в) Воспользоваться решением задачи 3.18. б) Вос
пользоваться решением задачи 3.11 (п. а)).
3.135. Использовать результаты задачи 3.134.
3.136. Условные распределения £ и ц при условии | + 'П ==2
совпадают. Если P {| £ + ri — г \ < е} = 0 при некотором 8 > 0, то
условное распределение g или т] при условии i + r \ = z не опре
делено.
3.138.
Обозначим через г\ число белых шаров в первой вы
борке. Тогда по формуле полной вероятности
п
P(i=m) = 2 P ( n - 0 P { 6 = « ln = 0 .
3.139.
Найти условную плотность распределения г| при фик
сированном £3.
3.141. Вводя индикаторы событий, показать, что
M x„ = nP { 1 / i s S i n
И
Л
И§у2 < §12 для / = 2,
п},
и вычислить последнюю вероятность, используя независимость
5i, . . . , Ей и формулу полной вероятности.
3.142. Использовать условные математические ожидания и
формулу Dt = M t 2 — (М т)2.
3.143. Представить Р
и Р {£ > х] в виде инте
гралов по промежутку [х, оо).
3.144. Положим |* = 1, если в испытании с номером t появи
лась 1, и £* = 0 в противном случае. Для условных математиче
ских ожиданий tn0= М { v 00 I Ei = 0}> mj = М {v 00 |gx = 1} составить
еистему линейных уравнений, используя равенства
M { v 00| ii = § 2 = 0} = 2,
М {V qo |E l— 0, £2 — 1} — 1 + /И1»
M{voo|Ei = l» Е2= 0} = 1 + т 0,
М {v001Ei —Е2— 1} = 1+ mi
158
159.
и формулу (3.18). Найдя из этой системы т0, т1у получаемMv00= pmt + qm0.
3.145. Для условных математических ожиданий
m0 = М {v l u l i i = 0 }, т 1 = М {v l u |
/Яц = М {vUi 1
= 1},
= 62 = 1 }
составить систему линейных уравнений. Найдя из этой системы
т0 и тъ получим Mvm = qmQ-\-pm1. См. также указание к за
даче 3.144.
3.146. См. указание к задаче 3.144.
3.147. Пусть £ / = (точки A lf . . . , А п лежат на дуге A f i
длины х (направление от А( к С — по часовой стрелке)}. Искомое
событие есть В1 (J . . . (J Вп. Показать, что В / П В / = 0 при i Ф /,
и найти Р {Bi |Ai = X } .
3.148. Указанное в условии событие не происходит тогда и
только тогда, когда длина дуги, содержащей А ъ . . . , А п, не пре
восходит половины длины окружности. См. задачу 3.147.
3.149. Если Вп — событие, описанное в задаче 3.148, то
{v
= Вп. Для вычисления Mv и Dv использовать задачи
3.54 и 3.55.
3.150. Найти длину дуги, на которой должны быть сосредо
точены точки Аъ . . . , Аю чтобы событие, указанное в условии
задачи, не выполнялось. Использовать результат задачи 3.147.
3.151. Если длина дуги АгВ равна л?, то {£ > х} = { А 2, . . . , А п
не принадлежат дуге А-^В).
3.152. Использовать формулу полной вероятности
2т
р йх > х< 1а > </)= 5 Р
^I ii = г>
(z) dz>
X
где р ( г ) — плотность распределения
и указания к задаче 3.151.
3.153. Использовать формулу полной вероятности
P ( l i > * i.
ч ) =
2т
= J
х2
tk > %k I£i = *} pit (г) dz,
Xl
метод математической индукции (no k) и результаты задач 3.151
и 3.152.
3.154. Воспользоваться результатом задачи 3.153 и тем, что
Р (1 it ^ ^1» •••» 1 /^ ^ %k)
= Р {1/у ^ xj
(/ = 1, . ••» к) у \т > 0 (ш ф
, £#)}.
159
160.
3.155. Заметить, что v = 01+ . . . + 0 „ , где ( 0 / = 1 } = { § / > Д},{0 / = О} =
Д}. Далее использовать задачи 3.54 и 3.55.
п
U (gft > х}.
3.156. Заметить, что {г)„ > х } =
Использовать
k= 1
формулу ( 1. 12) из введения к гл. 1 и результат задач 3.153, 3.154.
3.157. Использовать задачи 3.156, 3.57 и равенство
k= 1
О
О
3.158. Пусть а , (5, у — длины дуг ВС, СЛ,
А В,
Использо
вать равенства 5 = ~ (sin а + isin (5+ sin у),
p = 2 ( sin -| -+ s in - | + s i n Х ) ,
2S
а .
P ,
у ,
r = — = COS y + C O S Y + c o s y ~ l ,
результаты задачи 3.151 и свойство аддитивности математиче
ского ожидания.
3.159. Показать, что М ( 5 „ |S^ = s} = s, и, пользуясь выпук
лостью вниз функции f ( x ) = x 2, что
М {S* I S k = s} 3s (М {S „ I S k = s} ) 2 = s2.
3.160. Ввести случайную величину
min {k: 15^ |^ s e },
n+1
если
,
шах
| 5 ft | ^ e ,
l < k< n
если
шах
l < k< n
|5Л| < е ,
и оценить снизу
п+ 1
DS„ = MSn =
2
k—1
Р {т = А }М {Й | т = * },
используя результат задачи 3.159.
3.163. Получить рекуррентную формулу для М£Л, используя
интегрирование по частям.
3.164. Представить каждую часть неравенства в виде инте
грала по интервалу (л;, оо) от ее производной и сравнить подын
тегральные выражения.
3.167. б) Заметить, что
.^
^ч
/Infc-MIn ЕЛ„ /In «-М InIN
V
Найти M in g
160
v ra i
)
\
K dR
и D in g , используя результаты задачи 3.166.
/
161.
3.169. Воспользоваться тем, что случайные величина £ и — 5одинаково распределены.
3.170. Разложить cos 5 в ряд Тейлора по 5 и с помощью
результатов задачи 3.163 найти математическое ожидание каждого
слагаемого. При вычислении M c o s 25 предварительно перейти
к функции от двойного угла.
3.171. Воспользоваться результатами задач 3.169 и 3.170 и
равенством М sin2 5 = 1 — М cos2 5.
3.172. Вычислить (М cos 52+ «М sin |2)2 = (Me1’1*)2, записав эту
величину в виде двойного интеграла и затем переходя к поляр
ным координатам. При определении знака квадратного корня
найти знак 1ш
, делая в интеграле замену переменных и = х 2
и рассматривая интегралы по и от 2nk до 2л (6 + 1), £ = 0 , 1, . . .
3.173. Найти плотность совместного распределения гц, т]2.
3.174. а) Использовать
равенство
Р ( — 5 < х,
|5 | ^ 1 ) =
= Р(£<*,
б) Найти Р (5 + 11= 0).
3.176. а) — в) Воспользоваться независимостью 5 и rj; г) вос
пользоваться решением а) и симметричностью двумерной плотно
сти распределения (5 , *п) относительно начала координат; д), е)
вычислить с помощью интегрирования двумерной плотности.
3.178. Воспользовавшись тем, что плотность сферически сим
метричного нормального распределения инвариантна относительно
поворота вокруг начала координат, повернуть прямоугольник
так, чтобы его стороны стали параллельны осям, а вероятность
попадания в него не изменилась.
3.179. Воспользоваться симметричностью двумерной плотности
относительно любой прямой, проходящей через начало коорди
нат, и ее инвариантностью относительно вращений вокруг начала
координат.
3.181. б), в) Найти плотность (5, т]) в полярных координатах.
3.182. а) Выразить искомую вероятность через плотность
в полярных координатах (см. задачу 3.180).
б), в) См. указания к задаче 3.178.
3.183. Заметить, что распределения случайных величин 5 и
— 5 совпадают.
3.184. Из результата задачи 3.183 вывести, что достаточно
найти р 00. Подобрать числа яь Ьъ Ь2 так, чтобы случайный вектор
£ = (£i> £2) =
^ i? i+ ^2^2)
имел сферически симметричное нормальное распределение с плот
ностью J - e - {x2+y2)/* и чтобы
2л
{5i ^ 0 , 5г ^
== {£1 ^
161
162.
Для вычисления p 0Q воспользоваться последним равенством исферической симметричностью распределения £.
3.185. Найти функцию распределения £k = max |£ / 1
1< i< k
3.186. Воспользоваться соотношением |М£ |< :М |£ | и резуль
татом задачи 3.119.
Глава
4
4.1. Заметить,
что если f x (t) = 0 при |1 1 < х, f x (t) = 1 при
\ t \ ^ x , то Р {| | | 3 * х } = м / * ( 1) и g ( t ) ^ z f x ( t ) g ( x ) .
4.4. Показать, что для любых в > 0 и /1 = 1 , 2, . . .
={|±±й ^ г мЧ>4и
и
и использовать приведенные во введении к гл. 4 условия выпол
нения закона больших чисел.
4.5. Применить результат задачи 4.4.
4.6. Показать,
что
D
“п ‘
^” = ( 1
(1 ))—
v -f-o
i \
a _т|_^jг /га“ 1*
п — >-оо, найти распределение —
ную формулу для Р || —
и использовать точ
^П |^ 8
4.7. Воспользоваться неравенством Чебышева и результатом
задачи 4.6. Рассмотреть случайные величины
Р{6 а= 0} = 1 - 2 - * ,
P {g * = 2*Cfta} = P { g ft = — 2*C^a} = 2 “ * " i ,
k = \ , 2, . . .
4.8. Оценить сверху дисперсии £ i + . . . + £» и г)1+ ' * * + Л « и
применить неравенство Чебышева.
4.9. Вычислить математическое ожидание, дисперсию Zn/Cn и
воспользоваться неравенством Чебышева.
4.10. Заметить, что
? « ==*2“ ( ( 5 i + •••+ i n )2— ( l i + •••+ £я))
и что поэтому
> 1
1
+ Т
162
I
^
(
Г
> 1 }+ р i
I
it2
}+
" Z in - V > т } ■ <"
163.
Оценить первое слагаемое в правой части (1) с помощью неравенства Чебышева, а второе и третье— с помощью неравенства из
задачи 4.1 для функции g (x ) = J*|.
4.11. Утверждение задачи можно вывести из закона больших
чисел.
4.12. Применить закон больших чисел.
4.13. Воспользоваться результатом задачи 3.124 и неравенст
вом из задачи 4.1.
4.14. а) Показать, что Mv < оо.
б) Ввести случайные величины
=
. . . + %«» п = 1, 2,
где %/ = 1, если происходит Лу, и %/ = 0 в противном случае.
Показать, что P { v ^ v „ } = l, /1= 1, 2, . . . ; вычислить математи
ческое ожидание и дисперсию v „ и с помощью неравенства Чебы
шева убедиться в том, что для любого N < оо
lim
P { v n > N } = \.
4.15.
Показать, что предположение «существует такое N < оо,
что Р {v > N } < а — 8 < а» приводит к противоречию при вычис
лении математического ожидания случайной величины v ', совпа
дающей с v при v ^ N и равной 0 при v > N, двумя способами:
а) исходя из условия v' < : N, б) исходя из соотношения
оо
оо
П= 1
4.16. Связать события Ап со значениями случайной величины,
имеющей равномерное распределение на отрезке [0, 1].
4.17. Показать, что если v 8 — число одновременно происхо
дящих событий {| \п— £ | > е}, я = 1, 2,
то
и применить лемму Бореля — Кантелли (задачу 4.14).
4.18. Показать, что выполняются условия задачи 4.17.
и применить лемму Бореля — Кантелли (см. задачу 4.14).
б) Использовать соотношение
4.20.
Найти D ( ( £ х + . . . + §„2)/п 2),
Чебышева и результат задачи 4.17.
применить
неравенство
163
164.
4.21. Найти D (£„*+ 1+ £„2+ 2+ •••+ Ы » использовать оценкуМ
Р {шах {gi, £„
Sm } > е} <
2
i =1
р
> *}
неравенство Чебышева и результат задачи 4.17.
4.22. Вывести утверждение задачи из результатов задач 4.20
и 4.21.
4.23. а) Применить метод математической индукции (по п).
б) Найти
lim
p { l i + - - - + S» = * + l }
4.24. Показать, что можно воспользоваться результатами за
дачи 1.40 и что
P { x i ( A ) > n} = P { A n N },
Р { т 2 (Л0 > n} = ? { C n>N}.
При нахождении предельных распределений полезно соотношение
In ( 1— х) = — х-\-О (х2), х — > 0 .
4.25. Представить вероятность Р {т]„ < х) (0 < х < 1) в виде
суммы интегралов от плотности рg (х);
к каждому слагаемому
применить теорему о среднем.
4.26. Показать, что для любого е > 0 можно указать конеч
ный набор { 6lf . . . , 6,я} непересекающихся отрезков так, что
(
р
т
€ .U
6/ 1 ^
\
т
1— е и плотность р^(х) на
(J
6 / непрерывна
и ограничена. Далее воспользоваться решением задачи 4.25.
4.27. Воспользоваться равенством tg/z£ = tg ^ jx
и Ре_
зультатами задач 4.26 и 3.4.
4.28. Используя тригонометрическую форму записи комплекс
ных чисел, показать, что t n = tg (п arctg £), и применить резуль
таты задач 4.26 и 3.4.
4.29. Использовать неравенства из задачи 3.164 и определение
условной вероятности.
4.30. Использовать равенство Р { x w ^ х) = F n (х) и асимптотическое соотношение
lim
( 1 — —^ = е ~ с .
соV
пJ
4.31. Используя оценку
l ax+ ...Ч -а п
! P i + . . - + fc.
Ра
ш
1 <
“ ft
Ра
k = \ t ■..., ft,
max
1< k < п
,!
165.
показать, что для любых xi, х2, — оо < x t < х2 < оо,lim Р I х г < —
ГС-> °о {
°п
^ x 2\ — F (х 2) — F ( x t) .
)
4.32. Ввести независимые одинаково распределенные случай
ные величины £lf £2,
P{£fc = 0} = P { S * = l } = V 2, k = \. 2, . . . ,
и положить х „ = ? 1+ ?2+ . . . + л, /1 = 1 , 2, . . . Применить
формулу Стирлинга для доказательства того, что при k , /г — ►оо,
*= я + 0 (/я ),
In Р
Р {g„ = *}
о
4.33. См. указания к задаче 4.32. В отличие от задачи 4.32
нужно положить K„ = £ i - f - . . . + £ в л — 3/г.
4.34. а) Воспользоваться неравенством
Р ( Л £ ) < т т { Р ( Л ) , Р (В)},
справедливым для любых двух событий Л, В .
б) Использовать определение непрерывности
переменных и результат п. а).
функции
двух
4.35. Показать, что последовательности
. . . 6^л>)/п
при п — ►оо сходятся по распределению к at (г = 1, 2), и при
менить результат задачи 4.34. В случае а) сходимость &Л) к об
следует из закона больших чисел (см. введение к гл. 4), в слу
чае б) — из задачи 4.13.
4.36. а) Воспользоваться тем, что для любого е > О
{лГС
х
8» I
I^ 8} — {'ПпЧ"
х* I
I^ 8} —
s {% < я-f-e,
и тем, что
Р { Л } — Р { £ } < Р { Л В } < Р {Л }.
б) Доказывается аналогично а).
4.37. При вычислении Р {£ „ > х}
воспользоваться соотноше
нием lim ( 1— е) 1^8 = в " 1.
8 -»■ О
4.38. Заметить, что тк можно представить в виде суммы k не
зависимых случайных величин, распределенных так же, как §.
Воспользоваться неравенством Чебышева.
4.39. Значение Мт вычислялось в задаче 3.142, Чтобы найти
предельное распределение т, заметить, что
166.
используя оценкуD I S i+ •••~b
a| > ej><
;p {v < n } +
1+ ••*+ 1/7 — a\ > e
sup P
m> n
}
показать, что второй сомножитель в ( 1) сходится по вероятности
к 1, и воспользоваться п, б) задачи 4.36.
4.40. Заметить, что случайная величина тд имеет такое же
распределение, как сумма l i + . . . + £v» в которой £х, £2, ••• h v
независимы, glf £2, ••• распределены так же, как
a v имеет
геометрическое распределение с параметром q. Далее при решении
п. а) использовать задачу 4.37, а при решении п. б) — задачу 4.39.
4.41. Первая оценка следует из неравенства Чебышева. Для
доказательства второй можно ввести индикатор %л события А и
воспользоваться результатами задач 3.131, 3.60, неравенством
Коши— Буняковского и переходом к дополнительному событию.
4.42. Используя задачи 4.41 и 4.39, показать, что нахождение
предельного распределения q?i сводится к применению задачи 4.37.
Далее, с помощью задач 4.36 и 4.41 показать, что предельные
распределения qx-i и q%2 совпадают.
4.43. Убедиться в том, что процесс работы прибора удовлет
воряет схеме, описанной в задаче 4.42, и что для искомой слу
чайной величины т и случайных величин т х и т 2 из задачи 4.42
справедливо соотношение
P{t i<
t <
t 2} =
1.
4.44. Применить результат задачи 4.43. Использовать аппрок
симацию пуассоновского распределения нормальным.
4.45. Использовать определения указанных видов сходимости.
При построении примера рассмотреть такие независимые случай
ные величины 1П9 что P { | „ = | } = l — /i“ 1>
\ln— l \ > n } = n ~ l .
Вычислить М (£ „— £)2 и использовать лемму Бореля— Кантелли
для доказательства того, что
P { nH m J ln- S I = 0} = 0 .
4.46. Если
F (х)
и Fn (х) — функции распределения £ и %п
*
4е
( п = 1 , 2, . . . ) соответственно, F (х) и Fn (*) — обратные функции
а случайная величина £ имеет равномерное распределение на от
резке [0 , 1], то последовательность 1^ = /^ (£) сходится к %' = F* (£)
с вероятностью 1.
166
167.
4.47. а) В случае, когдасходится к £ по вероятности,
воспользоваться равномерной непрерывностью f (я) на любом
конечном отрезке и включением
{I f ( ! « ) - / ( £ ) I > 8}<={| gIз * Т) и {III < т, |% „-% |> в'},
справедливым для любых е > О, Т < оо при некотором г' = е ' (е, Т).
Случай сходимости с вероятностью 1 рассматривается аналогично,
а случай сходимости по распределению сводится к любому из
рассмотренных с помощью результатов задач 4.45 и 4.46.
б) Рассуждения проводятся так же, как в п. а), но при по
строении множества, на котором f (я) равномерно непрерывна,
нужно исключить из отрезка [— 71, Т] окрестности всех точек
разрыва / (х).
4.48. Существование величины £ = lim £„ следует из моноП - ► оо
тонности последовательности
а равенство М£ = а — из интег
рального представления М£ (см. задачу 3.60) и из теоремы о
монотонной сходимости (см. введение к гл. 3).
4.49. а) Показать, что если Д ^ (/г ^ 2 ) — минимальный по длине
отрезок из тех, на которые отрезок [О, 1] разбивается точками
h
Sfc-i. а I А* |— его длина, то 4 i + i S A j (k = 2, 3, . . . )
и М|
|— ►0 при k — ►оо.
б) Вычислить М£ и М§2, пользуясь тем, что условное распре
деление | при условии £i = * совпадает с распределением х% при
х ^ г/2 и с распределением 1— ( 1— *) g при х ^ 1/24.50. а) Показать, что P {lim | — g „ _ 1 |= 0 } = l , и восполь00
зоваться леммой о вложенных отрезках.
б)
Воспользоваться тем, что условное распределение £ при
условии £,i = x совпадает с безусловным распределением х (\— £).
4.51. Представить случайную величину
в виде,
ЬпЦп ( а п)
допускающем применение задачи 4.36.
4.52. См. указания к задаче 4.51 и ее решение.
4.53. Показать, что для любого е > О
lim р /1
п -* 00
(I
— ая — I » — Д» I > Д =0>
I
Ьп
)
есливыполнены условия в). При построении примеров, показы
вающих, что условия а) и б) не обеспечивают совпадения предельu Т>п ” &п
Till
о
ных распределении
— - и ------- ;— , рассмотреть случайные ве°п
Ьп
личины %п — Ьп1 -{-ап> гДе случайная величина | имеет стандарт
ное нормальное распределение, и подобрать соответствующим об
разом последовательности ап, Ьп, ап, Ьп.
167
168.
4.54. а) Рассмотреть случайные величины(1 — %п) Сп9
п = 1, 2,
где Xi» %2» . . . — случайные величины, независящие
от 1, р {Хп = 0 } + Р {х « = 1} = 1.
оо
б) Сравнивая М | =
показать, что
J
00
^ x d P { l * £ x } и M£w= ^ xdP {1п < , х } 9
—00
—00
за счет выбора достаточно большого Т интегралы
l* | d P { | | | < 4
и
J
lx\> Т
| * | л » { 6» < * }
\х\> Т
можно сделать сколь угодно малыми, а разность интегралов по
области {| л: | < Т ) при п
оо стремится к 0.
4.55. а) Рассуждая так же, как в п. б) задачи 4.54, пока
зать, что
оо
lim ( М п— М ) =
П ->■ 00
lim
Т —
>
■00 fl
lim
[ x 2dP {| %п |^ л :} ^ 0.
00 у,
Построение примера, в котором М > М , провести аналогично
п. а) задачи 4.54.
б) Случайные величины
удовлетворяют ус
ловиям п. а).
4.57. Случайная величина
имеет биномиальное распределе
ние с параметрами (я, р ).
4.58. а) Использовать равенство
= ф(Л) ( 1).
б) См. определение производящей функции и ее свойства.
1
в) Использовать равенство ^ za d z = -
, а > — 1.
о
4.60. Показать, что 0^ = т 1+ т 2 + . . . + т ^ , где Ti, . . . ,
—
независимые случайные величины, распределенные так же, как ве
личина тг в задаче 4.59.
4.61. Сравнить ряды
оо
Mz£=
c™z\pmqn~m*n и
n=m
1
- ~ — mzs.
^
4.62. Пользуясь результатом задачи 4.61, найти производящие
функции распределений glf £2, 1з и их суммы.
4.63. а) Воспользоваться формулой полного математического
ожидания.
б) Использовать результат п. а).
4.64. Найти Р {g i = g2= 0 } , P { £ i = 0}, P {g 2 = 0}.
168
169.
4.65. Представить <pg (z) в виде степенного ряда и воспользоваться правилами почленного дифференцирования рядов и неот
рицательностью коэффициентов ряда.
4.66. Сопоставить k- щ испытанию вектор (е^ х,
еk, n)>
k — l, 2, . . . , я, где eftt y = 1 , если в k-м испытании появился / - й
исход, и e^f/ = 0 в противном случае. Воспользоваться равенством
п
•••» ^п, n ) —
(£ я , 1»
2
( 8 fe, i»
•••»
n )
и свойствами производящих функций векторных случайных величин.
4.67. Использовать результат задачи 4.66.
4.68. Воспользоваться формулой полного математического ожи
дания и результатом задачи 4.66.
4.69. Воспользоваться тем, что ф (г) — аналитическая функция
в | z ) s ^ l , ф (1) = 1, и что ф (z) разлагается в ряд по степеням z
с неотрицательными коэффициентами.
4.70. Представить фх (г) и ф2 (г) в виде степенных рядов по z,
ф3 (г) и ф5 (г)— в виде степенных рядов по ф (z); показать, что
коэффициенты разложения ф4 (z) в ряд Маклорена неотрицательны
только в случае, когда ф (z) = const.
4.73. Вычислить характеристическую функцию l i + . . . + ?«.
4.74. Использовать формулу полного математического ожида
ния и свойства характеристических функций (производящих функ
ций).
4.75. Вычислить производящие функции M z l , Mz *\ * =■ 1, . . . , m,
и заметить, что если выполняются условия задачи, то Mz& =
= Mz^1. . .Mz^m.
4.76. а) Использовать соотношение
2nnj
k, если n делится на k,
0 в противном случае.
б)
Заметить, что {£ при делении на k дает остаток т) =
= { £ — т = 0 (m o d /г)}, и воспользоваться п. а).
4.77.
Заменить
случайными величинами £,•— остатком от
деления
на 3, найти распределение и характеристическую функ
цию
и воспользоваться результатом задачи 4.76.
4.78. Воспользоваться независимостью |i, . . . , £и.
4.79. Представить
в виде интеграла и оценить его
снизу, пользуясь положительностью и монотонностью показатель
ной функции.
4.80. Использовать задачи 4.78 и 4.79.
169
170.
4.81. Пусть l n = О, если \хп ^ n — [in, и | „ = 1, если |х„ < /г — |i„.Тогда
% = 0 — £я) Ню 4 " in ( п
Показать, что Р {|
—
М-п)= М-тг~\~
(Л
2[ХП).
* ^ C l nn b } = 1, где С > 0 — некоторая
постоянная. Воспользоваться результатами задачи 4.80.
4.82. Применить формулу полной вероятности.
4.83. Воспользоваться неравенством
|
— Me17"1 1 <
М | eit% — е“ о 11 « 5
< Л * -* „| Р {| Е | < Г }+ 2 Р {| 5 1 > п -
4.84. Представить / (^) в виде суммы действительной и мнимой
частей и воспользоваться условием задачи и четностью функции
cos х.
4.85. б) Показать, что разность двух независимых случайных
величин, имеющих равномерное распределение на отрезке [0, а " 1],
имеет плотность р а (х).
в)
Использовать формулу обращения для преобразования Фурье
(см. введение к гл. 4) и результат п. б).
4.86. Показать, что описанная в условии задачи функция f(t)
k
может быть представлена в виде / (t) = р 0+
2
P i max ^ — а* I *
i= 1
где k — число звеньев ломаной (графика
f ( t ), £ ^ s 0 ), аъ
. . . , а&
Ръ •••» Pk > 0» Р0+ Р 1+ •••~\~Pk = 1* Далее воспользоваться ре
зультатами задач 4.82 и 4.85.
4.87. Рассмотреть последовательность
(t ), / 2 (t), •.. харак
теристических функций, удовлетворяющих условиям задачи 4.86 и
таких, что lim f n (t) = f ( t ) для любого t t |£| < оо. Далее вос-
п -»■ оо
пользоваться теоремой непрерывности для характеристических
функций (см. введение к гл. 4).
4.88. а) Разложить fi (t) в ряд Фурье и убедиться в том, что
коэффициенты этого разложения определяют распределение веро
ятностей.
б)
Заметить,
что / 2 (0 = *
g1
» и получить разложение
/ 2 (0 в ряд Фурье с помощью результата п. а).
4.89. Использовать результат задачи 4.88.
4.90.
Заметить,
что
функции
f ( t ) = fiAelt^
и
g{t) =
= Melt (^1+
связаны соотношением f k ( t ) = g ( t ) и что, со
гласно задаче 4.83, функции g (t) и f (t) непрерывны.
4.91. Показать, что Ме1'^ = 1 тогда и только тогда, когда
Р {^ /(2 зх) — целое число} =^=1,
170
171.
р(лс), указанную4.92. Показать, что если £ имеет плотность
в условии задачи, то
оо
1— / ( t f ) = 2 ^ ( l — cos tx) р (х) dx = o (| 1 1)
о
при
t-+ 0,
и поэтому f (0) = 0. Для оценки интеграла разбить его на два:
от 0 до Т и от Т до оо — и использовать неравенство 1— cos
< : у 2/2 и асимптотическую формулу для р ( х ) , х
оо.
4.93. Показать, что функция u ( t) = R e f ( t ) четная и при у с
ловиях задачи удовлетворяет соотношениям и' (0) = 0, |и" (0) |^
< оо. Далее, пользуясь интегральным представлением
для и (t), показать, что
и " ( 0 ) = — lim
г о г I*
= — М|2.
4.94. Воспользоваться результатом задачи 4.93 и оценкой
(M |g| )2 < M | 2.
4.95. Использовать результаты задач 4.84, 4.91, 4.94.
4.96. а) При вычислении функции распределения
перейти
в интеграле к полярным координатам.
б) Воспользоваться результатом п. а) и задачей 4.90 для вы-
ittf
числения Me
4.97. Найти сначала характеристическую функцию гамма-рас
пределения с параметром а = 1 , затем (пользуясь задачей 4.90)
для а = 1/<7, <7= 1, 2
затем для a = p/q (р, <7= 1, 2, . . . ) и,
наконец, с помощью теоремы непрерывности— для произвольного
а > 0.
4.98. Найти характеристическую функцию
4.99.
Найти
характеристическую
функцию
распределения
Й1. •••.£*).
4.100. Воспользоваться теоремой из курса линейной алгебры
о приведении симметричной квадратичной формы к диагональному
виду с помощью ортогональной замены координат.
4.101. Используя формулу Тейлора для In (1— х), найти пре
дел логарифма производящей функции gi” *+ •••+ In* при п
оо.
4.102. Рассмотреть случайную величину £, имеющую равно
мерное распределение на отрезке [0, 1], и построить такие функ
ции f p (x), g p (x), х £ [ 0 , 1], что случайная величина f p {£) распре
делена так же, как
g p (£ )— так же» как Л» и
р V p (?)= g /> Q = fe }= min {P { ! = * } . р{*1=^}}>
k = 0 > Ь ••
174
172.
4.103. Тем же способом, что в задаче 4.102, построить понезависимым случайным величинам £lf . . . , £п, имеющим равно
мерное распределение на [0 ,1 ], случайные величины
...,
и максимально совпадающие с ними независимые случайные ве
личины г]!, . . . , % , имеющие распределения Пуассона с парамет
рами pi,
рп соответственно. Далее воспользоваться соотно
шением
Ш + ---+ | п Ф
+
U {li Ф п/}
i- 1
и свойствами распределения Пуассона (см. также книгу: А. А. Б ор о в к о в . Теория вероятностей.— М.: Наука, 1976, с. 117— 120).
4.104.
Рассматривая
непересекающиеся
события
вида
• •A tq* u •
iN -q } = {
ГДе { Ь
Щ \ {Н
»'?}
N
__
и А — событие, дополнительное к А, показать, что 5^ = S С> { В Ч}
Q—k
6 = 0 , 1, . . . Подставить эти выражения в правую часть равен
ства, указанного в условии задачи, и привести подобные члены,
изменяя порядок суммирования.
4.105. Разложить производящую функцию q>(z)=M z£ по фор
муле Тейлора (с остаточным членом в формуле Лагранжа) в точке
z = 1 и заметить, что <р (0) = Р {£ = 0}, ф Ш (1 )= /п л и ф(й )( г ) ^ 0
для любых fe = 0, 1, 2, . . . и z £ [0 , 1].
4.106. Заметить, что если ф (г ) = Мг&, то ф(w>(z) = M£fnlz£“ '1,
т. е. ф(и) (0) = я!Р {| = я }. Далее рассуждать так же, как в за
даче 4.105.
00
4.107. Заметить, что если ф (z) = Mz£ , то ^
Р {£;^г я} z " ” 1 =
/2=1
=
(ср. с задачей 4.70). Далее рассуждения аналогичны
проведенным в задачах 4.105, 4.106. Равенство
&■_ 1 — ф (z) I
dzk
1— z
_ ф < А+1>(1)
\z= 1 ~ ’
6+ 1
установить, используя формулу Лейбница и формулу Тейлора.
4.108. Воспользоваться неравенством из задачи 4.106.
4.109. Воспользоваться задачей 4.108, выбрав в качестве £
случайную величину, распределенную по закону Пуассона с па
раметром К.
4.110. Представить случайную величину |я/ (п, N, s) в виде
суммы индикаторов
(if (п , N , s ) = XI1’ + Х(2’ + . . . + X(N>
172
173.
и воспользоваться -формулой задачи 3.66 для факториальных моментов. Для исследования функции / / (я) = М ц / (я, N, s) рассмот
реть отношение / / (я-|- 1 )/// (я).
4.111. Использовать задачу 4.104.
4.112. Воспользовавшись результатами, полученными при ре
шении задачи 4.110, показать, что при указанном предельном
переходе выполняется соотношение min (я, N — n) = o ( N ) . Далее
использовать
явные формулы
для факториальных моментов
Hi (я, N, s) и задачу 4.109.
4.113. Представить [лг (я, А') в виде \лг (я, W) = % i+ . . . +% дг,
где X/ = 1» если /-я ячейка содержит ровно г частиц, и Х* = 0
в противном случае. Вычислить факториальные моменты |хг (я, N),
используя результат задачи 3.56, и применить утверждение за
дачи 4.109.
4.114.
Так
как
{|хг (я,
А0 + |лг + 1 (я,
# ) + . . . = 0} =
= {v r (АО > я} c r {jjlг (я, Af) = 0}, то при
Р {Иг (и>Ю= 0}
с,
^I** (я, JV)=o| — 1
(1)
выполняется соотношение Р {v r (N) > п}
С. Соотношение между
я и N, при котором справедливо (1), и значение С найти с по
мощью задачи 4.109.
4.115.
Если jLio1} (я, N) — число
строк, в которые не попало
ни одной частицы, а |42) (я, N) — число таких
же столбцов, то
случайные величины fXo1} (я, N) и fXo2; (п, N)
независимы и их
предельные распределения можно найти с помощью результата
задачи 4.113, а х (я, N) = \i(o } (п> АО |42> (я, N).
4.117. Применить центральную предельную теорему.
4.118. Применить закон больших чисел ицентральную пре
дельную теорему.
4.119. Использовать результаты п. а) задачи 4.118 и п. б) за
дачи 4.36.
4.120. Ввести случайные величины ед / (1 ^ i < N, / = 1, 2, . . . ) :
/ = 1 , если в /-м испытании появился £-й исход, и 8 д / = 0
п
в противном случае, и заметить, что Л»= 2
/
N
( S
/= 1 VI- 1
\
°*е/.1 )• Д алее
’ J
воспользоваться независимостью внутренних сумм и центральной
предельной теоремой.
4.122. Найти предел логарифма характеристической функции
(Е л -* )//Г .
«73
174.
4.123. Представить Sn } в виде суммы п независимых одинаково распределенных случайных величин и воспользоваться цент
ральной предельной теоремой.
4.124. Показать, что tAelt^ Sn
б " ^ 2, п - + о о , для любого
U| < °о, используя независимость £„ lf . . . , 5ЙВ, равенство
и
оценку
Sn2
max
М |£ |3 ^ (D£)3/2
l < fe< n
D£,j, k
(из
которой
можно
вывести,
что
0, n - + со.
4.125. Использовать результат задачи 4.124.
4.126. Использовать результат задачи 4.124.
4.127. Воспользоваться методом производящих функций для
нахождения предельного распределения ч\п при п —►оо.
4.128. Характеристическая функция распределения \п!А п при
п —>- оо должна сходиться к характеристической функции пре
дельного распределения.
4.129. Заметить, что {Nf < k} = {£i + . . . + >
t}, и восполь
зоваться центральной предельной теоремой.
4.130. Используя результат задачи 3.46, представить %Ш) в виде
суммы т независимых случайных величин. Для доказательства
асимптотической нормальности (£(/я)— М^(ш))/
показать,
что выполняются условия задачи 4.124 (при этом удобно применить
результаты задачи 4.73). Второе утверждение п. б) вывести из ре
зультата п. а) и задачи 4.53.
4.131. Заметить, что если
(у)— функция, обратная к F (х),
то, согласно задаче 3.5, распределения £(т) и Т7- ! (1— ехр { — а ^ ) } )
совпадают (здесь £ а ) ^ . .
— те же случайные величины, что
в задаче 4.130). Далее воспользоваться утверждениями п. б) задачи
4.130 и задачи 4.51.
4.132. а) Показать, что хт не зависит от v 0, v lt . . . , v m- i , вы
числив Р [ х т > п |v 0, v lf . . . , v ^ - Д ; для нахождения Р {х т >
воспользоваться формулой полной вероятности по значениям
— vt
и равенством Vfc = T i + . . . + т ^ .
б)
Из точной формулы для Р { х т > \ т- 1— v m- r ) получить
двусторонние неравенства, воспользовавшись оценкой
-г4
1+ х
^ “Г
— ^ ~л—7— ,
1— ху
1+ у ’
0 ^ у ^ х ^ 1.
*
4.133. Найти предел логарифма производящей функции
— k,
используя результаты задачи 4.132.
4.134. Для нахождения предельного распределения использо
вать утверждение задачи 4.124, а для вычисления моментов — полу174
175.
ченные в решении задачи 4.132 равенства v ot = T i + . . . + t т (гДеTi»
— независимые случайные величины) и формулу для
производящей функции x k.
4.136. Пользуясь симметричностью распределения |, предста
вить 1— bheli% в виде интеграла от 0 до оо. Чтобы исследовать
асимптотическое поведение 1—
при t —►0, разбить этот ин
теграл на два: от 0 до Т = Т (t) и от Т до оо— и оценить первый
интеграл по модулю, а при исследовании второго использовать
асимптотическую формулу для р (х) при х —> оо.
4.137. Используя формулу обращения для характеристических
функций (см. введение к гл. 4), показать, что распределение с харак
теристической функцией е ~ а \* ' имеет плотность р ( х ) = — 2 *
зт а I х
4.138. Показать, что плотность распределения случайной вели
чины 1/|х удовлетворяет условиям задачи 4.136 с а = = 2 и С = кр (0).
Использовать задачи 4.135, 4.137 и теорему непрерывности для
характеристических функций.
4.139. Воспользоваться свойствами характеристических функ
ций и тем, что £i + £ 3 = 2&E'
4.140. Заметить, что / а, &(я) лишь постоянным множителем
отличается от плотности суммы двух независимых случайных вели
чин, имеющих распределения Коши с параметрами а и Ь. Рассматри
вая характеристические функции, показать, что эта сумма сама
имеет распределение Коши.
Глава
5
5.1. Найти Р 2.
5.4. Найти рх = ? ( % = 1 |т|2= — 1). Р г = р ("Пз == И % = Ь Tfe =
= -!)
5.5. Вычислить Р {|Л0 ( п + 1) = / 1[*<> (Л) = &Ь
1= 0, 1,
N,
и Р {(л0 (« -h 1) = ^ I Цо(л) = ^ fx0 (п — 1) = ^i, . . . , М-о (0) = kn) при
любых допустимых значениях klt .
kn.
5.6. См. указания к задаче 5.5.
5.8. Показать,
что матрица ||р/у |)8 ^
—-дважды стохастиче
ская, т. е. что в ней суммы элементов как в любой строке, так и
в любом столбце равны 1.
5.9. Показать, что при фиксированном значении §* распреде
ление g /+1 не зависит от g0, h , . . . ,
5.10. Построить кусочно-постоянные функции g ( y ) и / (х, у)
так, чтобы при любых /, / £ { 1 ,
N} мера множества тех зна
чений у у при которых g ( y ) = j, / (г, у) = ], была равна соответ
ственно p j0), p i] .
175
176.
5.11. За состояние принять число очков грани, на которойлежит кость. (Сумма очков на противоположных гранях равна 7.)
Выписать матрицу вероятностей перехода; применить теорему о
финальных вероятностях.
5.12. Заметить, что р/ уП+ i = a /n для любого / = 1, . . . , п и
что поэтому распределение тп совпадает с распределением тп —
= min {t = 1, 2 , , . [ £ * = 1}, где £1э £2» •• •— последовательность
Бернулли,
Р { £ * = 1} = а /п,
Р {£* = 0 } =
1— а / я ,
* = 1 , 2 ...
Воспользоваться задачей 4.37.
5.13. Заметить, что Р {т 1= 1 } = 1. Для вычисления m0 (/V) =
= М {Тдг| z0= 0}, А7 = 1, 2, . . . , составить и решить системы линей
ных уравнений для
(/V) = М {тдг |z0= k}, k = 0, ± 1 , ± 2 ,
пользуясь формулой полного математического ожидания (разложе
нием по значениям гг). Сократить число неизвестных, замечая,
что m/г {N) = m - k (N).
5.14. Так же, как в задаче 5.13, составить систему линейных
уравнений для mk (N)> k = 0, 1, . . . , N — 1. Получить общую фор
мулу для m k ( N ), рассматривая в случаях N = 2, 3 значения
m0 {N) — mk (N), k = \ , 2, . . . , N — 1.
5.15. Используя формулу полной вероятности (разложения по
возможным значениям £(1)), составить систему линейных уравне
ний, которым должны удовлетворять m0, mv . . . , тдг, и убедиться
в том, что указанные значения т ^ являются единственным реше
нием этой системы.
5.16. Так же, как в задаче 5.13, составить систему линейных
уравнений, связывающих p k% д г (^ + 1 ), Pk- ь Лг№» Pk+1, N (t) и,
пользуясь монотонностью по t величин p iw (t), перейти от этой
системы к системе линейных уравнений относительно
6 = 0,
1, . . . , N. Вывести из этой системы, что отношение —
4 N)~ 4 N
-\
не зависит от k, и воспользоваться равенствами л ^ = 0 , зх
= 1.
Аналогично получить формулы для зх^0), 6 = 1 , . . . , N.
It
5.18. Найти матрицу вероятностей перехода Р цепи Маркова
и проверить, что зхР = зх, где зх = (зх0, я ь . . . , зхдг), и что
Jt0+ J t i + . . . + з х д г = 1. Использовать равенство CkN = C ^ ~ k и ме
тод производящих функций.
5.19. б) Используя формулу полного математического ожида
ния (разложение по значениям ^ в классе несущественных состоя
ний), составить систему линейных уравнений для величин т,- =
176
177.
= M {x | g 0 = t}, t = l,в нашем случае
2.
Решить эту
систему и заметить, что
M T = P ( g 0= l ) m 1+ P (go = 2) m2.
в) Аналогично п. б) составить системы линейных уравнений
для
, p f ] и для p f \ p f K
г) Заметить, что если +• =
lim Р {|* = / 1£о = /Ь / = 3, 4, 5, 6 ,—
/ — *• оо
предельные вероятности для цепи, начальное состояние которой
принадлежит существенному классу, то
я/ = Р ( $ „ = 1 )р < “ '<?/ + Р ( | „ = 2 ) ^ а >9/>
/ = 3, 4 ,
я / = Р ( 1 о = 1) р Т ь + Р (5о = 2) p f q j ,
/ = 5, 6.
5.20. Пусть С\, . . . ,
А,
— собственные Еекторы (векторы-столбцы)
соответствующие А,ь
динаты а
...,
...,
вектор-столбец
имеет коор
и все координаты вектора-столбца e j равны
0, кроме / - й координаты, равной I. Если еу— a^Cx-f- .. . + a n \ i, то
arn) = Amej=Am ^ a (/>Cft= j
fc=l
fc=l
5.21. Использовать указания к задаче 5.20 и приведение
матрицы А к жорданоЕой нормальной форме.
5.22. По собственным числам матрицы Р и по значениям
Р , Р 2, . . . , p N - i мы можем составить систему N линейных урав
нений относительно коэффициентов с/у в формулах задач 5.20 и 5.21.
5.23. Использовать результат задачи 5.22.
5.24. Представить
(t) в виде суммы индикаторов: v 1 (t) =
= 0 i + . . . + 0 f , г д е {0 й = 1} = {£& = 1}, {0ft = O} = {|ft = 2}, k — 1 ,2 ,...
Заметить, что М0fc = P/i(fe), М0/;0г = P ji (k ) Pv.i.1— Щ (1
Используя результат задачи 5.23: ру1 (k) =
ГДе |е,& |<
а тР
^ | 1 — а — Р |fe, показать, что
м {vt (О I |0= / } = г | -р t (1 + о (1)),
1
1
м Н 23 (0 ||0= / } = ( м {vt (О I Е0= / } ) » . ( + о ( )),
D ( V ! (/ ) I i o = / ) =
= М {vl** (t) | l o = / } + М {v t (0 | i 0= / } -
-(M {v1(0|6. = /}), = o(<*).
Проводя вычисления более аккуратно, можно показать, что
о ы
( 0 1 6 в = / } = с * ( 1 + о (1 )).
177
178.
6.25. Использовать результат задачи 5.24 и неравенство Чебышева.
5.26. Использовать равенство
N
N
Л/
дГ= S
nkPkj—-^r= ^
k —\
5.27.
Рассмотреть
/1 — е2
= (
{pkj
дГ J
k —\
матрицы
Р = ^ ^ 28
^
и
=
s2 \
e
1—е / ПРИ 8 ^ ° -
5.28. Показать, что последовательность £>п— гп+л— zn обра
зует цепь Маркова G 4 состояниями. Найти явное выражение для
k-и степени переходной матрицы этой цепи, представляя ее в виде
разности двух коммутирующих матриц 1 и G (т. е. удовлетворяю
щих условию IG = GI). Далее вычислить М£* и воспользоваться
равенством
2tj= £o+ £i + •••+£и-1«
5.29. а) Использовать лемму Бореля — Кантелли (п. а) задачи
4.14) и формулу Стирлинга.
б) Убедиться в том, что п. б) задачи 4.14 неприменим. Вы
числить Mv двумя способами: вводя индикаторы событий { S „ = 0 }
и вводя случайные величины Ti = min
1: « S „ = 0 }, T^+ i =
= min { я > г*: «Sw= 0 } , &= 1, 2, . . . (которые удовлетворяют уело»
ВИЯМ { V ^
= {Tfc< оо}).
5.30. Заметить, что компоненты S „,i, . . . ,
$ вектора Sn
являются независимыми реализациями величин, рассматривавшихся
в п. б) задачи 5.29. При s ^ 3 использовать лемму Бореля— Кан
телли, при s = 2 рассуждать так же, как в п. б) задачи 5.29.
Глава
6
п
6.1.
Положим уь = х ь — а, у — — ^
Уь• Показать, что s2 =
п k— 1
п
= — Ц - ^
( у ь — у )2. Найти Ms2. Д оказать, что Ds2= 0 ( l //z ) при
k= 1
Я — * 00.
6.3. См. задачу 3.69.
6.4. Использовать независимость Х( и s?.
6.5. Величина s2 является состоятельной оценкой Dxt (см. за
дачу 6.1). Показать, что s2jDx1 при я —>■ оо сходится по вероят
ности к 1. Воспользоваться решением задачи 4.36, б).
178
179.
6.6. Выразить величину mu через x'j = x j — Mg, у) = г/у — Mr).Доказать, что Dmu = О (1/п) при я — ►оо.
6.7. Найти Мр*, Dp*. Использовать неравенство Чебышева.
6.8. Используя теорему Муавра — Лапласа и результаты задач
6.7* 4.36, б), доказать, что при п —►оо
р{
у
ф(дс)*
6.14. б) Написать функцию правдоподобия с М а / =
Мс/ = а + 6.
с, tAbi = b,
6.15. Воспользоваться результатом задачи 6.1, центральной
предельной теоремой и задачей 4.36, б).
6.16. Оценки ЛГ и Аг зависят от общей оценки г3 и, следо
вательно, нельзя воспользоваться решением задачи 6.3. Из усло
вия несмещенности МЛ* = Л получим: c1-j-c2= 1. Отсюда Л* =
= а + р [cx Z j-f (1—-cj) z2] + yz3. Найти DA* и подобрать сг так,
чтобы дисперсия была минимальной.
6.20. Воспользоваться формулами
Х2 = Х[2]-\-Х,
ХЪ= Х[Ы-\-ЗхМ-{-Х,
х* = х Г41+ 6л ;1:з:,-(-7л:Г2]-(-л: (х[Ь] = х ( х — 1 ).. . ( х — k-\- 1))
и решением задачи 3.85.
6.21. Использовать результат задачи 3.43.
6.22. Использовать результат задачи 3.46.
6.23. Использовать результаты задач 6.21, 6.22, 3.43, 3.46.
6.24. Использовать результат задачи 3.43.
6.29. Использовать квантили иа нормального распределения:
1—Ф (иа) = а.
6.30. Воспользоваться решением задач 3.85, 3.90 и формулой
(k+ 1)/N
6 = 0, 1, . . . , N — l.
6.31. Воспользоваться решением задач 3.90, 6.30 и указанием
к задаче 6.30.
179
180.
ЧастьГлава
1.19.
ill. РЕШЕНИЯ
1
Легко проверяется, что
!+ ( w -
- j . (
!+(w-
,=ш (
)■ )-,п
—
2_
т ] + N2
_ т ]+ Р
Покажем, что Р 2 < Р 3 при N ^ 3 :
-и ш -и х '-тк га + га ))1.22.
Нетрудно проверить, что
{ X 3 + К 3 = 0 (mod 3 ) } = {X = К = 0 (mod 3)} U
U { X ==— У = ] (mod 3)} и {X = — У = — 1 (mod 3)},
т. е.
Р { X 3+ К3 = 0 (mod 3)} =
Так как
Щ
+
= J V и функция
f(x)=x(a— x ) = l —
(2)
ТО
Р|Х. + 1 '. _ С ( ш о й З ) ) < ^ ( [ 4 ] ’ + 4 - ( » - [ | - ] ) ’ ) -
Далее, если М х — множество чисел, дающих при делении на 7
остатки 1, 2 или 4, М 2— множество чисел, дающих при делении
180
181.
на 7 остатки 3, 5 или 6, то для любого п £ М г число гР при делении на 7 дает остаток 1, а для п £ М 2 число гР при делении
на 7 дает остаток — 1. Поэтому
{* з + Уз — о (mod 7)} = [ X == У г
и {X €
0 (mod 7)} (J
Г £ М 2} и {X € м 2, К € Afj.
и
Р { X 3+ К3 = 0 (mod 7)} =
Пользуясь равенством в (2) и тем, что для любого N ^
1
получаем
Р {X 3 + У3 = 0 (mod 7 ) } ^
*
м
т
'
+
*
и
(
'
-
т
)
Ч
)
-
= ^ ( ? - » т + 4 ш ч -
®
Из (3) и (5) следует, что
N* (Р { X 3
К3 = О (mod 7)} — Р { X 3 + K3 = 0 (mod 3)}) 5=
ч и - [т ])(- 4 (и +т ) ) —
при N > 7, Для N = 4, 5, 6, 7 соотношение Р { Х г -\-У3 ^
= 0 (mod 7)} > Р { Х 3+ К3 = 0 (mod 3)} проверяется непосредствен
но с помощью формул (1) и (4).
1.25. Если Ех симметрична Е 2 относительно S 3, то
1з — l l = £ z — l s = d i ,
"Пз— Tl l = n 3— ^3 = ^2
(I)
для некоторых целых чисел di и d2l не равных одновременно 0 и
удовлетворяющих условиям |di |^ п, |d2 1< ; п. При фиксирован181
182.
ных <*1 и d2 число троек карточек (|lt гц), (g2, r]2), (g3, ц3), длякоторых выполнено (1), равно (2/2+ 1— 2 | |) (2/2+ 1 — 2 |d2 1).
Суммируя по dj и d2, находим число троек попарно различных
карточек, для которых S i симметрична S 2 относительно S 3:
2
(2 п + 1 -2 К | )(2 п + 1 -2 | < Ы ) =
dt, d2——п
df+d^O
= ( 2 n + 1) 2 2
( 2 n + l - 2 r f 2) +
d2= 1
+2
2
(2 n + l-2 d ,)( 2 « + 1 + 2
dt=l
\
= 2 ( 2/2 +
+ 1 ) — я (я +
1) ( n (2/i +
2
(2rt+ 1— 2d2) ) =
d2=l
1) — n ( n + 1)) + 2 ( n (2n +
/
1)) ( 2 /2 + 1 + 2 (я ( 2 я + 1) — n (Я + 1))) = 4/г2 (/г + 1)2.
Так как общее число упорядоченных троек
карточек есть
( 2 я + I )2 ( ( 2 я + I)2-
1) ( ( 2 я + I ) 2 — 2 ) =
попарно различных
4 п ( я + 1) ((4 я ( я + I ))2— 1),
то искомая вероятность равна
я ( я + 1)
^
(4/1 (я -|—1)) 2— ! *
1.65.
Граница Д ABC пересекает ровно т окруж н остей , если
А находится между S2m- i и
(при /72 = 0 — внутри Slf при
2т— 1 < п < 2/тг+1 — меж ду S n и
и поэтому
( 1 /я 2,
8 m //i 2,
(2/2— 1)//22,
0,
Глава
2.18.
т
= 0,
1^
т
< [(/г— 1 )/2 ],
/72 = /2 /2 , /2 четное,
/72 > /2/2.
2
Если /2 = 2, то из условий задачи
P(^l)= Pl» Р(^2)= /?2» Р(^1^2)=PlP2
следует независимость Лх и Л2.
При /2 = 3 уже можно привести пример совокупности зависи
мых событий, удовлетворяющих условию задачи:
Р(Л1Л2Л3) = Р(Л1Л2Л3) = 1/8,
Р ( АгА 2А ъ) = ? ( i M * 4 3) = 1 / 8 - е ,
Р
(^1-^2^з)= Р (Л 1 Л2Л3) = 1/8 + 8,
Р <АхА%Аъ) = 1 /8 + 2 6 ,
182
Р (Л1ЛаЛ8) = 1/8— 2еэ
183.
где 0 < е< ;1 /16. В этом случае Р (Л /) = 1/2, i = 1, 2, 3, Р (Л1Л2)=== 1/4, Р ( А 1А 2А 3) = 1 / 8 , но Р (Л 1Л3) = 1 / 4 - е ^ Р ( Л г) Р ( Л 3).
2.19. Пусть события A lt
А ft удовлетворяют условиям
задачи. Оценим снизу число элементов множества Q. Для любого
S j= 0 или 1 ( t = 1, 2, . . . , £ ) , Р j
набора (8f,
_
где
Ж°> = Л/, Л(.1>= Л1*, т. е.
1
1
k .
ПЖ i* Ф 0 .
i= i
. . . , Sfc) Ф (si» •••» £ft)события
1
П
>0»
Так как при (elf . . .
и П
непересека
ются, и число различных наборов (еь . . . , 8ft) равно 2й, то
k < log2 п. Экстремальным примером является Q = {(8X, . . . , 8ft):
8j = О ИЛИ 1} С Р {(&ь . . . , 8ft)} = 2 ^ и Л1* = { 8 / = 0 } > i = 1, . . . , £ .
2.20. Пусть на подмножествах Q = {1, 2 , . . . , п} задана веро
ятность Р (-) (Р ({/}) = P i , i = 1, 2, .
ti) и выделена совокуп
ность попарно независимых событий Ль . . . , Лft. Сопосгавим
каждому событию Л/ вектор a i £ R n:
ai = (s.i'> V"p~i> 82* Vlh, •••. e-n V p n l
'= 1
k,
в
где e/l) = l, если j £ A { , и e /l, = 0
противном случае. Покажем,
что если события А ъ . . . , Лft попарно независимы, то векторы
аи . . . , aft линейно независимы. Ввиду попарной независимости
Лх, . . . , Лft
(a,-, aJ) = ? { A iAj } = ? { A i} ? { A f }
при
1ф\
(1)
и (а{у а 1-) = Р { Л /} > i = 1, . . . , п. Как известно из курса линейной
алгебры, векторы аг, . . . , аft линейно независимы тогда и только
тогда, когда линейно независимы векторы
bi=((ai, ax), [fli, а2), ... (щ, ak))£Rk,
i= 1, ..., k.
(Действительно, если
. . . + a kak = 0t то в силу линейности
скалярного произведения
+ a ft^ft = 0; обратно, если
a i ^ i + . .. + aftbft = 0, т. е. (а,, агаг+ ... + айай) = 0, t = 1, . . . , £ ,
то
(0^ + ...+ a ft a ft ,
. . . - {-a kak) = 0 t
или с а д Л - . . .
...+ a f t a ft = 0.) Согласно (1) векторы 6г* имеют вид
Ь/ = Р {Л /} [ ( Р { Л 1} # . . . , Р {Л й}) + (1 — Р {Л,-}) ^ ],
где
— единичный вектор t-й координатной оси. Поэтому при
любых числах а1у . . . , ад
ai^i + ••
=
= (о^Р { Л х } . . . + a ftP {Лft}) (Р {Лх}, . . . , Р { Л^}) —
}—
Л-осхР{Лх} (1 — Р{ЛХ})
. *. 4-afcP {^4/г} (1
Р {^ й }) ^ft,
183
184.
т. e. a i ^ i + . . . + а/гЬл = 0 только в случае, когдасс/[(Р{^/})2Ч-РМ,} (1—Р{Л£})] =0, 1=1, ...,£.
(2)
Так как по условию Р {А{\ > 0 , 1 = 1 , . . . , k, то из (2) следует,
что a x = . . . = a ^ = 0, т. е. векторы Ьи . . . , bk линейно незави
симы, т. е. линейно независимы векторы а1г . . . , ak £ R n. Однако
это возможно только при k ^ n .
Приведем пример совокупности, состоящей из п > 3 попарно
независимых событий. Положим
y4i = { l , • « ., я ),
и пусть Р {1} = 1— (п— 1 )*,
удовлетворяет условию
Л/ = {1, i),
Р {t} = *,
1— (п— 1 )л ;= (л :+ 1 — (п— 1) х ) 2,
i = 2, •••, tit
i — 2,
т. е. л:
п, где * > 0
п—3
( п - 2)2
Нетрудно проверить, что такие события Ль . . . , А п попарно не
зависимы, если п > 3. При п — 3, согласно задаче 2.19, на Q =
= { 1 , . . . , п} нельзя задать такие события Ль Л2, что Р {Л гЛ2} =
= Р { А 1} Р { А 2} и 0 < Р { Л / } < 1 , i— 1, 2, и поэтому при п = 3
можно построить только 2 попарно независимых события A lt Л2.
(При этом либо Р { Л х } = 1 , либо Р {Л 2} = 1 . )
2.54. а) Согласно теореме Муавра — Лапласа
Эти предельные значения и являются приближениями для иско
мых вероятностей.
б) При p = q = \ j 2 из формулы (2.11) находим
P { i « = fe} = C n 2 -* ,
А = 0 , 1...........п.
(1)
Отсюда и из равенств
Р {| £юо— 50 | ^ 5 } — Р {45 ^ |100 < 55),
р (I ёюо— 60 1^ 5} = Р {£ 100 < 45} + Р {1 10о ^ 55} =
= 1— Р { 4 6 < | 100< 5 4 }
184
185.
находим55
P { 4 5 < 6 loe< 5 5 } = 2 - w o
V
q 00 =
*= 45
/
JL с 5° - ь \
= 2-iooqo^l + 2 £
-^ |-j =
- # ( ' ^ i ? ( - + s ( ' + s “( ' + 4i ’ ( ' + s ) ) ) ) ) /-*50
= 9,15635
Используя
находим
уточненную формулу Стирлинга
■оо.- г ш
где О ^ 0 Ь
i = 3, 4, 5,
2100
02<
1.
(см.
.
(2)
стр.
9),
{та и -ш л я п }'
Поэтому
при некоторых
0/,
| 0/| «^ 1,
L _ exp i
-L + -® 2 -\ 5 У2п
I 400 П , 8.108f “
•_ Л
~ 5 ]А 2 ^ \
1
l
0з ,
04 \
400 ' 1 ,8 -105 ' 2-3992/
0 ,9 9 7 5 + 0 6- Ю- s
_
<3>
Из (2) и (3) следует, что
Р {4 5 С £ 100С 55} = 0,7 2 8 7 4 + 0б. 10"*,
|0б | < 1.
Аналогично находим, что
Р { Ц юо- 5 О | ^ 5 } = О ,3682О +07.1О -*,
|07 | < 1 .
Отличие значений вероятностей, полученных в п. а), от истин
ных значений объясняется двумя причинами: заменой допредель
ных значений вероятностей предельными, а также тем, что собы
тия {| ?ю о— 5 0 | < 5 } и {| Sioo— 50 I ^ 5} пересекаются.
2.55. а) То же, что в предыдущей задаче,
б) Аналогично решению задачи 2.54 получаем
P { U i 2 8 - 6 4 | « 4 | /"2} = Р { 5 9 < £ 128« 6 9 } =
-HO+f (1+1('+Г7(‘+|(1+®)))))=
= 9 , 5 0 5 6 3 ^ = 0 ,6 6 9 0 6 + е - 1 0 - » ,
|0|<1,
181
186.
и таккак 4 У~2 — число нецелое, то
Р {| Ii28 — 64 13* 4
=
= 1— р{| Si28— 64 I < 4 j/~ 2 } = 0,33094— 0. Ю- 5 ,
|0 | < 1.
Глава
3
3.47.
Согласно
задаче 3.46 соответствующие вариационному
ряду Е<1) < Еш < • •• < Sod (построенному по
ные величины
Ai = ?(i)»
^ k ==^>(k)
^>(k—i)»
.............g„) случай
k = 2, 3,
.
ti,
независимы и Д^ имеет показательное распределение с парамет
ром (п — k-\-1) к, к = 1 , . . . , п. Остается заметить, что
max {g ly . . . , g„} = g(w) = Д1+ Д2+ .•. + Aw
и что
случайные величины \ъ1к, 6 = 1, 2, . . . , п, независимы и
gft/6 имеет показательное распределение с параметром кК, т. е.
распределено так же, как Д „ » ^ +1.
3.49.
Введем вспомогательную случайную величину g3, не за
висящую от gx и имеющую распределение Пуассона с параметром
^2—
Согласно п. б) задачи 3.17 распределение Si+ ^ з совпа
дает с распределением g2* Поэтому для любого 6 = 0, 1, 2, . . .
Р « 2 < * ) = Р(Е1+Бз <Л ) =
k
=
2
/72=
P (5 e = m )P (6 i< k - m ) <
0
< Р (Ь < «Р (5 з < А )< Р (Ь < й ).
3.57. Пусть F - i (г/) = suр {л:: F ( x ) ^ y } ' t тогда, согласно за
даче 3.5,
1
М| = J F ^ i ( y ) dy,
о
т. е. M g — площадь области
Но
1
{(*, у):
0
00
^ F - ! (у) d y = ^ (1 — F (x))dx.
о
3.109.
о
Для любой последовательности х п f 00
I6l‘ / ( , 6 i< * „> tl6 l* По теореме о мажорируемой сходимости
М (| 1 1* /j| и < Жи|) f М 111*.
186
F _ 2 (*/)}.
187.
Так как^ l E I ‘ = M ( l i l ‘ / f l 6 l< je jl)) + M ( | i | * / {l8 | > je B }),
то М (i | |ft /{, | о
Хп}) Ф 0.
3.123.
Так как функция f (х) = \х\г при г ^ 1 выпукла вниз,
то при любом действительном х , согласно задаче 3.119,
M | *+ T )| r 3 s | M ( * + r i) Г = |лг Г.
Поэтому при г ^
1
м | Е + л Г = м (м {| 6 + г| П 6 })^ м | Е Г .
3.126.
б) Если ранг матрицы В равен г, то существуют такие
линейно независимые векторы blt . . . , bk_ r £ R k, что Bbi = 0,
i= l,
— г. Поэтому D ((b it Q) = (bi, Bb() = 0, i = 1,
— r,
т. e. P {(6/, £) = c*} = 1 для некоторых чисел съ . . . , ck_ r. Значит,
существует г-мерная гиперплоскость Lr a R k, ортогональная под
пространству, натянутому на blt . . . , b k_ n и удовлетворяющая
условию Р ( Б € М = 1Обратно, если существует ^-мерная гиперплоскость Lqa R k,
для которой P { § £ L ^ } = 1, то существуют линейно независимые
векторы Ьъ . . . , b k - g , ортогональные Lq, и числа clf . . . , c k _ q,
удовлетворяющие условиям
Р {(5 . bi) = Ci} = 1,
t = i, . . . , л - * .
Согласно п. б) задачи 3.125 тогда ВЬ( = 0, i = 1, . . . , 6 — <7, т. е.
ранг В не превышает q Так как по условию ранг В равен г,
то соотношение Р {g ^ Z .r _ x} = 1 не может выполняться ни для
какой (г— 1)-мерной гиперплоскости Lr ^ 1d R k.
Глава
4.12.
4
Так же, как в задаче 4.11, находим, что
{!<”>£с v .
i
} = р|
n Vz/n, e f
\
Ч + - - - + 1iff” !— j
( 1)
n y 2/ л
что случайные величины |£ Г |, . . . , | | Г | независимы и имеют
стандартное нормальное распределение; так как, наконец,
00
m U i"I = - 3 =
00
( х е ~ х ‘ /й d x = - % = Г e ~ “ d u = l / _ L
]^2nJ
о
j/lS J
о
D и г I= м ( | Г ) 2— (м| | Г |)а= 1 ■
~
У
„
*
< =0 ,
то стремление к 1 правой части ( 1) при п — ►оо следует из закона
больших чисел.
187
188.
Сравнение результатов задач 4.11 и 4.12 (с учетом сферической симметричности распределения £<” >) показывает, что при
достаточно больших п гиперсфера B y — ^ = { x £ R n: x l+ . . . + хп = А
и
поверхность
С^у—
^ = { x £ R n: |Xi | + . . . + 1х п | = п |/~2/л }
близки друг к другу: для любого е > 0 отношение (я — 1)-мерного объема множества тех точек х £ В у — Q, для которых отрезок
[(1 — S) л:, (1 + е )х ] не пересекается с С
объему
^
к (/г — 1) -мерному
, стремится к 0.
4.22.
Используя обозначение,
введенное в задаче 4.21, мы
получаем равенства
£i + ••• +£>»_ „ _
П
( £ i - a ) + . . . + ( i tK- p - a ) [ j ^ p
-
[7 1 ?
п = 1, 2, ...
r y -j
п
п
[У ~ п Г
Из результатов задач 4.20 и 4.21 следует, что
(
( £ ! - « ) + . . . + ( i [ ^ ] - a) [ ^ ] 2_
\
р \ Л т . ------------- Г 7 Ч 5-------------------Р/
J p L L G I .o },,,
значит,
что и требовалось доказать.
4.29. Согласно задаче 3.164 при х > а
7- ^ - g l < Р {£ > X) <
е-(*-а)У2<Я
V2n
\х— а
—
}
(x— a f f
т. е.
lim Р {| > х} У~2к e(x~ a)*/2a*
X—
*■ОО
любого у ^ О
=
1.
х— и
Поэтому
lim Р { ( I — х) х > у \% > х } =
—
“ Л
488
lim
Щ
> х + у х -'}_
т > х }
6ХР { “ 25» ( ( * + ^ ~ ~ a) S~ {Х~ а)2) } :
для
189.
4.41.Чебышева:
Первое утверждение является следствием неравенства
_
Р {| ^ л :| А }
Р {g ^ x t А }
1 „ г?.
р- p - j
< 7 Р
.
а2
Для доказательства второго утверждения введем индикатор собы
тия А:
Ха = 1» если А происходит, ^ = 0 в противном случае.
Тогда
М { 6 |Л} = ^
} = ± М & А= а + ± м а - а ) х А -
При F - i (у) = sup {t\ Р (g — а < /}
0)
г/} согласно задаче3.131
р
1
^ F _! (u) d«s£M (£— а ) х А <
5
о
(2)
1-р
а согласно задаче 3.60
1
а2 = D£ = М (£ — а) 2 = J F h (и) du.
(3)
о
Применяя к (2) неравенство Коши — Буняковского и пользуясь (3),
получаем
IМ (|— а) х а I <
( Р
;ш ах •{ J |
1
(у) |dy,
Iо
^
l-p
(
Г р
p
Г
« S m a x -j)/
^ F 2- i (u)du J du, у
l
о
ч
\ F - 1 {y)\dy\ <
о
)
i
^ F -i(u )d u
l-p
i
]
^ du> «s;
l-p
J
« 5 a V~p.
Отсюда и из (1) следует, что
I М {| | А ) — а |< а / У~р.
Если
(4)
то с помощью равенства
а = р М { 6 М } + (1 — р )М {6 | А}
и оценки (4), примененной к М {£ | Л }, находим:
1— Р
о
_ „ V l—p
р
J/1 T —j ,
р
189
190.
4.42.Рассмотрим сначала случайную величину
Из усл о
вий задачи следует, что образующие
слагаемые
£2>
независимы, не зависят от числа слагаемых v — 1, распределение
каждого слагаемого совпадает с условным распределением £i
при условии 8i = 0, и при q — >-0
Р {q (v — l)* s ^ x }— ► 1— е ~ х ,
х^гО .
Из задачи 4.41 следует, что
M {i(-|e/ = 0} = a + 9 ^ jQ L
(1 0 |< 1),
{= 1 ,2 ,...;
кроме того,
D { i f I е/ = 0} = М {if I е,- = 0 } - (М { I ; | е,- = О})2 <
Мf i
а2 +
„
Применяя задачи 4.39 и 4.37, получаем, что
lim Р { ^ Т £ ^ х } = 1—
x^s O.
Q-> 0
Покажем теперь, что предельные распределения случайных
величин qxi и qx2 при q — ►0 совпадают. Согласно п. а) задачи 4.36
для этого достаточно показать, что для любого б > 0
Р {? Е /< 6 | е /= 1 }-* 1 ,
q — ►0.
Но из первого неравенства задачи 4.41 следует, что
Р {ЯЬ > 6 1е ,-= 1} < q(^
4.51.
aq^ —» 0,
9 — 0.
Из условий задачи следует, что
( 1+ 9 + 1
8п &п)~-8п
ь пёп ( а п)
bn
V
VI
\) ) ;
ЬП
( 1)
I/ J
далее, так как функции wn (А) монотонны, то для любого 8 > 0
где vn ( •)— функция, обратная к wn ( ‘ ). Из условия
lim
П-+ со
590
wn (Л) = 0 для любого А <
оо
191.
вытекает, что lim vn (е) = оо для любого г > 0; поэтомуп—
►00
Л^Ы1|Х2!1)Ц“
(2)
для любого
что
е > 0. Из (1), (2) и результата задачи 4.36 следует,
lim р
п-+оо
\
( ln )— gn (ап) < х \ р
bngn (ап)
I
(х).
4.92.
Если М |g | < оо, то (см. введение к гл. 4) / '( 0 ) = iMS
по свойствам характеристических функций. Покажем, что если
распределение £ имеет плотность р ( х ) , указанную в условии за
дачи, то |/ ' (0) | < оо, а М |§ |= оо. Последнее соотношение оче
видно:
оо
2
оо
М | 1 1= 2 ^ хр (х) dx = 2 Л хр (*) dx-\- 2 Ц
= оо,
где O ^ a ( x ) < оо и ос (х) — ^1 при х — > оо. Для доказательства
соотношения |/ ' (0) | < оо покажем, что
| 1— f(t)\ = o(t)
при
t — >0
( тогда / ' (0)= lim - — /-2^ = (Л . Действительно, из оценки 1 —
t-+Q
V
— cos у
1
)
у 2/2 следует, что если
Т — * ос, T = o(\ t | -i),
то
1— f (t) 1= 2 J (1 — cos tx) p (x) dx —
о
*■)=■° ( w - +
w
* )
191
192.
Если Т — (| t\n |t\ |)- 1 ^2 при t — >-0 , топоследняя оценка дает
' - ' « - Ч и Н м ) - 0" '" ’
что и требовалось показать.
4.93.
Пусть u ( t) = R e f ( t ) ,
v (t)= lm f(t).
Из условия
|f n (0) | < оо следует, что |и" (0) | < оо и что и' (t) существует
в некоторой окрестности точки t = О и непрерывна при / = 0. Далее,
оо
u ( t ) = J cos tx dP
^ x},
— OO
т. e. функция
Тейлора
u (t) — четная-,
и поэтому
и '( 0) = 0 . По формуле
« ( 0 = l+ -J -« " (0 ) (1 + 0(1)),
п /АЧ
V
1— U (0
т*
Г
<—-0.
I — C O S tX
“ (0) = - / Г о ~ 1 * 7 Г - = _ /™ о 1
1ЧУ2
_
* * {£ < * >
— оо
Для любого х, 0 < |х | < оо, имеем
..
1— cos tx
,
/™ 0 ~1ьгч7
Г =
поэтому
= -
J *2c(P {g < x } = - M £ 2.
Таким образом, М £2 = |и" (0) |=< |f" (0) | < оо.
4.105. Пусть ф(ЛГ) ( 1) < оо. Разложим производящую функцию
оо
<p(z) =
*=о
{i = k} zk по формуле Тейлора в точке z „ = l с оста-
точным членом в форме Лагранжа:
*«-
1^
< - ■>*+***-,s i y - ' »
о < 0 < 1.
192
193.
Полагая здесь г = 0 и* € 10, 1], получаем
замечая,
что
Фс*’ (г) Зг 0
при
любом
N
Ф (0) = р {Е = 0} = 2
( - 1)* 2Т Г ^ + ( - »)^+1вдг+1.
ЙЛГ+13 * 0.
/г=0
Отсюда и из того, что <р(*>(1 ) — т ^ следуют неравенства, указан
ные в условии задачи.
4.127.
Математическое ожидание и дисперсия
непосредственно:
M i(tn> = 0,
вычисляются
D ^n ,= l.
Вычислим производящую функцию т]„, пользуясь независимостью
слагаемых:
Поэтому при любом фиксированном г
lim Мгл" = exp
exp
—§ ~ }*
Так как g*2 - 1 )/2 — производящая функция случайной величины
имеющей распределение Пуассона с параметром 1/2, a g(2" 1~ 1)/2 =
= M z” ^, то распределение г\п при п — ►оо сходится к распреде
лению разности двух независимых случайных величин, имеющих
распределение Пуассона с параметром 1/2:
lim
Р {г|„ = /г} =
V
Л
£ t >2mml
е ~ 1 /2 _________ 1_________ е _ 1 /2 ,
2 l ftl + m (|A| + т)\
6 = 0, i If . . .
4.136.
Так как
распределение £ симметрично,
= р (—*), то Ме“ lt^ — N\eu ^ = М cos t l и
т. е. р (х) =
194.
Выберем е так, чтобы выполнялось условие 0 < е < 3 — а , тогдгпри j 0 , используя соотношение 1 — cos и ~ и2/2 (и — * 0), находи*
(1 — cos tx) р (*) dx =
о
/ —8/2
*=2
J
оо
(1— cos tx) р (х) dx + 2
^
0
(1 — cos tx) р (х) dx =
/ - е /2
00
«= 0 ( / 2“ е) + 2
J
(1— cos и )р
Щ-ш
(1)
/1-8/2
Далее, используя условие р (х) ~ С |л: |“ а , | * 1 — ►оо, получаем:
при / 4 О
00
СО
С
( I — c o s m ) p ( - j - ) - у - = ( 1 + о ( 1»
j1
(1 — cos и) -С-“ _ а d u =
/1-8/2
/ 1 - 8 /2
: (1 + 0 ( 1)) C i * - 1 j '-~ ™ s и du.
(2)
Из (1), (2) и того, что 0 ( * * " * ) = о (f®6- 1) при t — ►0 и 0 < е <
< 8 — а < 2 , следует, что
оо
M « ^ - = l — 2 С | / Iе* - 1 (1 + о ( 1 » С 1
о
-1 “ du,
“
т — о.
Глава
б
6.28.
Обозначим через ег и е2 единичные векторы на осях
координат и положим £„ = z„ +1 — zn. Тогда z« = £0+ £ i + . . .+ £ n -i>
т, е. Мгя *=М£0+ . . . +
и последовательность £0,
••
образует цепь Маркова с множеством состояний {elf e 2 t — е2, —ex}f
матрицей переходных вероятностей
Л
1
194
г 1 /3
1 /3 1 /3
Оч
1/3
1/з ]
1 /3
1 /3 о
0 1 /3
О
1 /3 1 /3
1 /3 /
1 1
1ч
1 1 ч
1
1 1
1 )’
ч!
1 1
I /
1 /3
_L а __ п\
3 (
}>
J
/О
О
О 1ч
o J °О 01
ОО h
\1
ОО /
0=М
О
1° 1
195.
и начальном состоянием=
Чтобы вычислить
что при начальном условии Ео = е1
заметим,
(Р {С *= е Л )1 -1= (1 , о, О, 0)Р*
Так как IG=^G1 = / , то
k-\
( / — G)ft= 2 (— l)"»Cgl/ * - « » - h ( — 1)*G*;
m= 0
далее, / Г = 4Г-* Л Gk = Q при нечетном £ и
/1 0
/ 0 1
G *=£ = о 0
\0 0
0 0\
0 0\
10 )
0 1/
_
учитывая равенство
ПрИ четном
k-l
2
(— l )771 Ckl4k~ m = (4 — 1)Л— (— !)*,
нахо-
т =О
ДИМ
p * = - i ^ / — ( - 1)*
**4
> Т- е - при S o = ei
3я
1 .2 -4 -1 )*
Р{5*=в1}=
4-3*
’
_J_ _
PK* = «.} = P { C * = - « t—} =4 - J - - - ^ r .
р {£*= — ^i} =
1
2 —(-1 )*
4-3*
Отсюда следует, что M£fc = - i - е1 и
3*
п- 1
V*
1
1— 3 - »
Мги
гп ~ е 1 2 * Зт ~ в1 1 —
т= 0 '
3
Л
2 в1{
1 \
Зп )
5.29.
а) Согласно лемме Бореля — Кантелли (см. задачу 4.14)
достаточно показать, что
оо
2 P {S „ = 0 }< ~ .
пш 1
(1)
Но P {S „ = 0 } = 0 при любом нечетном п, а если n = 2kt то по
формуле Стирлинга при k — ►оо
Р { S n = 0} = cikPkqk ~
Pk4k
2 n k k 2k
(2)
V nk
При p Ф q имеем 4pq < 1, а отсюда следует (I).
195
196.
б)Х отя, согласно (2), при р = ^ = 1/2
P{S2* = 0 } ~
(* -* о о )
(3)
•о
и, вначит,
2
Р { ^ = 0} =
°°,
мы
не можем применить
лемму
п= 1
Бореля— Кантелли, так как события
являются зависимыми.
Введем случайные величины
{ 5 Я= 0 },
/1 = 1 , 2,
...»
x1= m in {n ^ l: S„ = 0},
Tft+ i = min {п > %k\ 5 Я = 0} ,
£ = 1, 2 , . . .
(в случае, если множество, стоящее под знаком min, пусто, следует
положить min равным оо). Из независимости и одинаковой рас
пределенности |lf £3> ••• следует, что случайные величины
Tfc+i— Tfc, & = 1, 2,
независимы, не зависят от
и распре
делены так же, как т х. Поэтому
Р {v ^
k) = Р {тк < о о } =
k- 1
= Р {т, < оо} Д Р {т,-+1— Х{ < оо} = (Р {т х < оо})*,
(4)
[=1
и, согласно задаче 3.54,
оо
Mv = V (Р {т, < оо })* = — — 1 — — - .
k?\
1— Р { Т ! < 0 0 }
С другой
ных случаях,
(5)
стороны, если
= 1 ПРИ
= 0 и %п = 0
то v = Xi + X2+ - . - » и в силу (3)
оо
в
оо
M v = ^ МХ « = 2 P { S 2ft = 0} = oo.
п= 1
fc=l
(6)
Из (5) и (6) следует, что Р { т х < о о } = 1, а тогда в силу (4)
Р {v ^ k) — 1 при любом k < оо, т. е. Р { v = оо} = 1.
5.30.
Заметим, что компоненты 5 Я>1, . . . , SnfS вектора Sn
являются независимыми реализациями случайных величин, рас
сматривавшихся в п. б) задачи 5.29, и поэтому при п — 2k
Р {S « = (0.......... 0)} = (Р (S n, ! = ( ) } ) * ~
и Р { 5 Я= (0,
0)} = 0 , если п нечетно. Значит»
оо
2 Р {5 „= (0 ,
В» 1
196
0)} < оо
00,
197.
при s ^ 3 и в силу леммы Б ореля— Кантелли Р {v < оо} = 1 приS ^ s3 . В случае s = 2, повторяя рассуждения из п. б) задачи 5.29,
находим, что /Av = oo, и если Ti = m in {/z: S w= (0,
0 )}, то
Mv = :----- FT7"*—
г.
Значит,
р (Тх < ОО} = 1 и P { v ^ 2:&} =
1 — Р (Ti < 00}
1
= (Р {'tt < oo})ft= 1 при любом k < оо, т. е. Р { v = оо} = 1.
Глава 6
6.17.
Из условия несмещенности следует, что с8 = 1— ct — с2.
Дифференцируя Dz = c l - \ - c l + ( l — c1— c2)2 + 2c1c2p по с% и c2t по
лучим для определения съ с2 систему уравнений
2с1 + (1 + р )с а= 1,
(l + p ) Cl + 2ca= l .
( 1)
а) Вычитая из первого уравнения второе, получим (1 — p)cL—
— (1 — р) с2 =
0 ,
или
ct =
c2.
Следовательно, с1 = с2 =
^ » с8=
= 1 ± 2 „ 0г= 1 ± £ .
з + р
з+ р-
б) Если р = — 1, то из первого уравнения (1) получим
1/2,
а из второго с2= 1/2. Следовательно, с3= 0 , т. е. в наилучшую
оценку включаются в этом случае только коррелированные оцен
ки Zi и z2. При р = — 1 величины z1 и г2 имеют вид z ^ a + g ,
z2 = a — I, где М£ = 0, D g = l . Таким образом, z = (zI + z 2) / 2 s= a.
в) При р = 1 уравнения в ( 1) одинаковы: C i + c 2= 1/2. В этом
случае Zi = a + g, z2 = a + £ , где Mg = 0, D £ = l . Таким образом,
очевидно, что при любых clt с2 (сх+ с2 = 1/ 2) и с3= 1/2 получаем
одно и то же выражение z = (a-f- £ + z3)/2 , и D z = l / 2 .
198.
Ч а с т ь IV.Глава
ОТВЕТЫ
1
1.1. 2/3. 1.2. Р ( Л ) = 1/1785 = 0,0005602..., Р (В ) = 1/3927=
=0,0002546...
1.3. 1/6.
1.4. 1/2, 3/8, 7/8.
1.5. Р ( Л ) = 1/3,
Р (В) = С™_22п ~ т ~ 2 3~ п
( 0 < т < п — 2),
Р (С) = С « 2 « - '» 3 - '»
(0 < ш < «),
Р ( Д ) = то!|у |!т 2 , р
(m0+ m i + / n 2 = /t). 1.6. 7/18 =
= 0,38888... 1.7. Р (/1)=°6,2г1, р2 (В) = 0,01, Р (С) = 0 ,2 7 .1.8. а) 0,504;
б) 0,432; в) 0,027; г) 0,036; д) 0 ,001. 1.9. PN=jj- Г-у]
у
( N - * оо).
К й + Ш - Ш )ш
- й <-й
(N —>. оо).
1.11* Если N = \ 0 k + l t то pjy=2k/N при / = 0 , p jv = (2£-f- l)/N
при 1
< 9, р д г = 2 (6 + 1)/Л7 при / = 9;
1/5 (X —* оо).
1.12.
Р л г = -Т
1.14.
_
?л г= 1 + 2 ( - 1 ) *
-1
(Л1—* -00). 1.13. Э .Ю - ^ - й + Ч .
J L
2> ГДе СуММИ‘
рования производятся по всем простым числам р х, р2,
lim g ^ T T f 1— V ) = 4 = 0 , 6 0 7 9 2 7 . . . ,
" y-V
P2J
n2
где произведение берется по всем простым р. 1.15. зх/ 4 = 0 ,7 8 5 3 9 8 1 ...
1 1
99
9
1*16. Рп+\— ~2
2 ' 10п ’ ^ » “ ft+3==2 ' Ю2^
2 - I0fe+”
199.
! -28* (4n (” +6)
^
- i -
iM -
q o5’ 6 ~ 10 = 0 , 15 50 45 3...;
1.27.
0,055252.
1.28. ^
62016
^ 1 -0 ,1 3 0 0 8 8 4 ...,
a>
в)
”+ 2 .
(5 /6 )^ = 0,1615055...?
1— (5/6)10= 0 , 8384944...
1.29.
^ = 0 ,0 0 0 0 9 9 9 5 ...,
99
^ -0 .1 4 8 4 2 5 7 ...
r mt Стг
C mN
A4t M 2 * • * M »r
1.30. 1) —
ес ли M
^
j+
... + М лг, n = m 1+ . . .
Cm
trii^i 0;
s» i +
E
( - d'
1.31. 1/2; 1/3.
v-i
( M — M k — . . . — M k ) l n]
£
-s—
^
1.32. СмС*}Г™м/СЪ, C™ocOT( l — а ) " _ /я , m = 0 ,
I, 2, . . . . n. 1.33. J - j .
1.34.
Ш | = 0 , 95 08 14 7...
если числа мужчин и женщин не равны друг
если
число мужчин
равно п.
^
U\CN+1
ХЛ1‘ »
.
о\
2)
другу;
1.35.
0,
2« + i __ 2
-------------- ?
С^п
2911
Y2T1256 ==^*00228986...
1.36.
л» ( 1 о 2
, /-,3
\
Л/!
3) ( т с М / - 1 + С д г +х) ДОЛГ+1’
4) 1* если n ^ N + l ; 0 , если я = 0 или п = 1; 1
дгС"]
—
,
если
1
2^ n < N .
1.38. 2
(— 1)г ( 1— г г ) " -
1=о
■)
,
'
,0
если я
четно
1
1
'
Слн-п- 1
>)w . f. “ 1" ' !1<А' - “ + 2>|" га
2) сед
мо- *>
-'AZ+m-.,I
п
четно,
1 - 3 9 . 1 ) 1 ------
' б ) ----------- л я --------- '
2« / ___
N \М
и 0,
П РО
.ТТН /г
П UPи
о т и п • в)
сЛ —т
_____
и
если
нечетно;
—i — }
,
NW \ 2 J
. . . // *v, v—- 1n\ w
Jl он
t«3 . .
.(
( N — 1 \ [п -П )
2 [-Г-)
{-Y-)
+n2
если
/V
} ’ если N
нечетно
l M • a) ^ w S (W- fe+1)C&]Mn"ft]’
'
[ m/2 ]
6)
Z (2^)[^ ( Л / - 2 ^ + 2 ) ^ ^ - 2Ч'
199
200.
пв )— Ц -5 5 2 2* ( - r p Y ^ JVl- Ч , если N четное;
(2W)M ^ 0
^ 2 '
если /V нечетное.
1.42. а) я “ ” ; б) (я — 1)“ - * C { ^ - " ; в) я " 1; г) я “ *. 1.43. а) 1/я!?
б) 0 , если среди /\, . . . я /* есть одинаковые! 1/ я ^ 3, если все j u
. . . ъ jk
различны; в)
1/я; г)
2 / я ^ ; д) 1/я. 1.44. Р„=*
- У ( - ' ) fe+lF “ ^ 1 _ T
*=1
а,
/г—ctj
^п ’
п(п— 1)’
,4 5 - а> т г г й
‘ *=i
1.46. Р {111< 4 = 2лг— 1 ( l / 2 < x s = S l ) ,
Р (Лг ^ А = 2*
(0 < л : < 1 /2).
1.47. a) min (х, 1) (* ^ г 0 ); б) 4х (1 — л:)
( х ^5 1/2); в) к х 2 (0 ^ л; С 1/2), 1 (x^ z 1/ Y 2), * 2
+ }T W - i
(0 < ;* ^ l/2 ), I
— 4arccos
r) i -ях*
(0 < * < 1 ), 1
2), x 2 ^-2 — arecos - i - ) -|- j / ' x 2— 1 (l < x <
(x ^
+
^ 2).
1.48. a) jc (3 — 2jc) ( 0 < x < 1 / 2 ) , 1 ( x 3 * 1/2);
6) 0 ( x < l ) ,
m in (x -U
1) ( x 5a l ) ;
в) 1— ( l — x ' f b f (0 « x < 1/ f /* 5), 1
( x S * l V 5 ). 1.49. tg (jt/8) = У 2 — 1 = 0 ,4 1 4 2 1 3 5 ...
1.50. P „ =
= t g ^ - t g ^ = g ( l + o ( l ))
* m
1.52.
f<
n r j.
f 1— 2 — tg
л \ 2
(n ^ cc).
cl
,
1.51.
3T
л
? если г < - - c t g y ; 0 при
k = 3 , 4, 6. 1.53. 1, если 0 ^ a , 1 — -i-arccos
1.55. Q* = Y
« < vr-F
1.И. Q , - l - | . r o . n ^ ,
Rw
где
X~ ( u ) '
состоящее в том,
,
it
— ctg -^ -,
Q r= | -,
Q r = ^ T = ° - 866025—
«S- | , Q W _ _ ± .
- i - s ( i + ‘) ,f W - I
Ak — событие,
a
1/ 6.
если l®l < « . О» если
0 < - а ; р ( а , 0) = р ( - J , о ) = 1 / 2 . 1.54. Qx = 1 Q ^ _ = l.
5/6,
■'
что
было k пересечений.
1- т ( ' - т ) ‘ - 4 ( 1- т ) ’
1.60.
200
■
/
4г2h+ й а ;
- ^ U = 0 , 707106...;
у 2
L
ft
- 0 _ = о 8660254
2 —u>oow^
-
201.
+1.62.
1f e P + r3 /
= 0 ,3 7 8 7 3 2 ...;
h
а) —
2 У (4г)2-(-Л2
2
в ) 4 = ^ г - = 0 , 4 3 3 0 1 2 7 ...
h
4
1.65.
; б) 1 ----- 1
-= =
2
2уТ7
1 .6 3 . 4 “ -----------7 = =
2
2 1 ^ 73
= 0,3244382...
1.64. J L ar c t g - | .
Р 0= 1/па,
P m = 8m /n2
(l< m < n /2 ),
Р„ /2 = (2и — 1)/n 2 (п четное), P m = 0
(m > п/2).
Глава 2
2.1.
2.4.
2.7.
1/3. 2.2.
N
1/7. 2.3.
1/19 ( t = 0 ) ,
2/19 ( t = l , 2............. 9).
2.5. M //V . 2.6. -г -, , , . / '
p/il / 2I (A^— / i — / 2)!
s
L.
3N
M
a) 1/5; 6) 1/5; в) 1/30. 2.8. a) 1/2; 6) 3/5; в) 4/7. 2.9. P {Л *} = ^ ,
p {fiA,j}
NW ’
= 0 ,3 9 5 2 ...,
p Xе А
,
^[2]
pi w
210
43
2
P { ^ 2 } - g i g = 0 , 2 0 4 7 . . . , Р { Л 3} = - д - .
2.11. 1) C^+atN[n^ N ^ N al N ^ + n‘ +1^i
2) 2 N[m]Ns/Nlm+1h
m> 0
3) ( Л ^ + Л ^ - ^ Л У Л ^ ,
^ = ^ + ^2 + ^ 8.
2. 12. а) Л/} £/* независимы при любых /, &; б) Л2, С2 независимы;
в) Л4, С4 зависимы. 2.13. Независимы пары Л/, Л / с i, / £ { 1 , 2 ,
5, 6}, и события наборов {Лъ Лб, Л6} и {Л 2, Лб, Л6}. 2.14. Только
при г ^ 0 ,
2/3 и г = 1/3. 2.15. а), б) Являются. 2.16. Л1Л2
и Л3 зависимы. 2.18. Является при п = 2; не обязательно яв
ляется при
3. 2.19. f c < ;lo g 2 /z. 2.20. k ^ n (/г > 3), &= 2
(/г = 3). 2.21. a) a ^ ; б) 1— (1 — P i)(l — Р2)- 2. 22. а) ( 1— a i) ( 1— а 2);
6) S s l — a i — ос2. 2.23. а) {C\ClJC% )2 = 0,0003115...,
(
6
2
V
C * C l s k/ C U j = 0 ,0 0 0 3 4 7 3 ...
2.24. </б{<7з+/>з</4(<?1 + Р1<?2)}. ГДе < 7i= l — Pi2.25.
1
= 0,3619047...
б)
2.27.
а)
р (1 — рх) (1 — р2) + (1 — р) сад л
Р (1 - P i ) (1 - Р з ) / [ Р (1 - Pi) (1 - Р
2.28. а), б), в) M/N.
2.29.
2) + (1 - Р ) « 102].
х/а.
202.
2.30.а) 0,573683; б) 0,7776829...; 0,8732712... 2.31. f - ^ 0 ,0 2 8 2 ,
Р а = 0,0428. 2.32. 0 ,0 2 7 < Р 1< 0 ,0 3 3 , 0,041 < Р 2< 0 ,0 4 7 . 2.33. 5/11.
2.34.
14/17 = 0,8235294...
2.35. 2 a p i/[2 a p ! + (l — а) (ра+ р 3)].
2.36.
а) v (1 — Р )Л Т 0 — Р ) + а ( 1— 7)1:
= р ( 1— a)/[p ( 1— a) + ( l — р)(1 — {$)].
2.38. а) 2/11;
— (7/8)2о = 0,980791...
2.40.
в)
2.41.
0,987204...
2.42.
6 )6 /1 1 ;
а)
в)
3/11.
0,348678...;
С?
2.39.
б)
P t/ qt^
1—
0,057395...;
^ 1 — 1 ^ = 0,00021137...
C n p m+ n qn ~ m. 2.43. (1 — p 2) N . 2.44. ( r q r - ^ p + q ^ N ,
S
б)
6) 0,9173...
2.37. 9о =
9 i = a p / [ a p + P (l — />)],
2.46.
2.45.
а) Ск
ыр г Ь ( \ - р г ) Х - ^
C ^ q r ^ ~ k ) ( l — q r)k. 2.47. а) pqs , б) (1— q3)pq*, в) ( 1 - g 3— Р93)Р93-
2.48.
qk = Ck
b+k2 - * - * ; q 0= 1/32, 9i = 3/32, <?2= 2 1 /1 2 8 , q3 = 7/32,
qA = 63/256,
96 = 63/256.
2.49.
C$+r2 - ' - “ . 2.50.
0*593126...
2.51.
536. 2.52. 0,26502. 2.53. 0,26424. 2.54. a) 0,68269, 0,31731;
6) 0,72874 , 0,36820. 2.55. a)
0,68269, 0,31731; 6)
0,66906,0,3
2.56.
0,95.
2.57.
0,846.
2.58.
a) 558; 6) 541.
2.59. 547.
2.60.
C ^ p V - *- 2.61.
2.62.
2.63. 9 : 0 ,5. 2.64. 9 a; 0,25. 2.65.
Q(n+m)/2 p(n+m)/t q(,n-m)/t ^ если
a) 7 /8 ; 6) 2/3; в) 1/3.
q (1 — p3) /( 9 + p 3); 0,7.
2.66.
— целое, 0 в противном
случае. 2.67. C&l (21) “ а (0,1)« (0,3)2=0,0054432... 2.68. р 1+ я р ? - 1рз0,76896. 2.70. C £ ‘ p™‘ ( 1— р 1)п ~ т К
2.69.
*.71.
*
У *.
т 21. . . т л-! * А2 \ 1— p i /
2.72.
а) я! ( j [ ftv l . Д
/ А/,
л?2
\-х /у,
V
J
лг2 .
П
б) ( я - п 2)1я21р1~П,р Ь где P / = P / i + . . . + P ^ .
(п — П2)!
гг
в) b i l \ . . . k 1Nx\ П
<=1, 2,
A l t ,
V77)
»
если
, и
••
=
N-k
= п — п2, 0 в противном случае.
2.73.
^
'
C tf-fcX
/=о
Х ( - 1 ) г ( l — 57^ - ) ” . 2.74. 3/4. 2.75. Р {03v + i = i } = l / a , ( = 1 ,2 ,8 .
2.76.
202
p i /( p i + p * ) . 2.77. а) 0*489142...; б) 0,295635...; в) 0,215222.«
203.
Глава3.1.
3
а) С = 1 / 2 ; б) р п (х) = 1/2 V 7 , 0 < л: < 1; в)
= 0,13098...
в)
3.2. а) 2 о х е ~ ах2 (х > 0);
а 2е ~ 0С^е°СХ~ х^ (— оо < х < оо);
=
б) a e ~ a V 1 l2 V~x (х > 0);
г) а е - ах/(1— е~ а) ( О ^ д : ^ 1);
д) 1 ( х € [ 0 , 1]). З.з. а) 1/2 ( * £ [ 1, 3]); б) е - * ( х > 0); в) ~ (1 ^
(— со < х < со);
г)
- j e ~ ' X' (— со < х < оо). 3.4. .L -}--L arctg •— ,
j - j q - j j - (— о° < * <
3.6.
со).
р^(х) = 0 в остальных точках;
при | х | ^ 1 .
p l (x) = l/2 при K | x | = s S 2 и
g ( x ) = x при | х| «^ 1, g { x ) — x j \х[
3.8. а) р _ 1, . = p i , . = 1/2,
р . ,_ i = l / 3 ,
р .,0= 1/4,
р .,1 = 5/12; б) ^ - 2 , i = 1/8, <7-1,о = 1 /1 2 , *7о,-з.^ 1/2» <7i,o= l/6>
<72>1= 1/ 8, остальные ^ />у- = 0 ; в) д _ 2,. = 1/ 8, q - i , . = 1/ 12, q0t.= l/ 2 ,
^ ’ . = 1/6 , ^2, .= 1 /8 ; г) ^ .f - ! = 1 /2, q . f0= q . f 1==1/4. 3.9. P { £ i = £ } =
= 0,1, 0 ^ £ - < 9 , Р {£2 = 0} — 0.55, Р {£2 = 1} = 0,45. Случайные
величины
и £2 зависимы. 3.10. Зависимы. 3.11.
(0 < х < 2а), 0 (х < £ [0 , 2а]); б) — ^ 1— |
в ) ^ 1п ^
(0 < х < а2), 0 ( х $ ( 0 , а2));
^ — *|)
(| х |< а ) , 0 (|х| > а);
г) 1/ 2 (0 < х « 1), 1/(2х2)
(хЗ* 1), 0 (х < 0). 3.12. а) х е~ * (х З зО ); б) -i- e ~ i* i (— оо < х < оо);
в)
е ~ х (х^Э= 0); г)
(х ^ 0).
3.13. - I min | l ,
х — 1||
( 0 < х < 3 ) ; 0 ( х $ [ 0 , 3]). 3.14. 1— е ~ * ( 0 « х < 1); <?-<*-!>— е ~ *
(1 ^ х). 3.15. а) 1— | 1— х | при 0 ^
1, 0 в остальных точках;
у2
3
/
3 \2
/3 ___у\2
б) у при O ^ x ^ l , -j— ( х — — J при 1 ^ х ^ 2, -— 2— ПРИ
23
2 ^ х ^ 3 , 0 в остальных точках; в) ^ = 0 ,9 6 0 3 3 ... 3.17. а) Р|1+ |2( * ) =
\т
= а 2х е ~ ах (х > 0);
б) Р {| 1+ | 2 = т } = - ^ - е - +
т = 0 , 1, . . . ,
/(vy\K “ ?■
А, = Я,1+Х ,г.
3.19.
3.20.
3.18. а (П_
е - ах (х > 0);
(0 «х « 1 ),
б) апе~“ »* (х > 0).
0
(х $ [0 ,
1]).
( и - 1 ) ( 1 - х ) » - 2 ( < Х х < 1). 3.21. 1— - ^ 4 a r c t g - l ^ I —
= 0 ,7 1 1 4 ,,.
3.22. р|1+ |>( х ) = 1 /2 , х € 1 0 , 2 ].
3.23. П и ?а (х, у) =
203
204.
~ 2П уТ
+ 2'(2ft'W
-
‘
{ * 4 - 0 2< l ) ; P | t ( * ) = l / 2 ( | * l < l ) - 3 . 2 4 . | +
3'25'
? ^ = ^ ' x*=h)==qll+tl~Zpi'
/ь ^ , 5
P ( т ! = /) = Р ( t 2 = 1) = Я1~гР,
1. Случайные величины
независимы. 3.26. а) зависимы; б), в), г) независимы. 3.27. Р(0 = /,
(jfa = l—
v = ft) = ( i y , ~ 1 . - g - ( / = I . 2 , 3 t 4; п = 1, 2 , . . . ) ;
/ 1 \«-12
Р (v = n) = ( -g- J
-g -.
Р (0 = / ) = 1/4,
Случайные величины v и 0 независимы.
N
3.28.
б)
Р (т2— / 2, . . . » T/v— /уу)— Л
Р
— //г)» Р ftk — /& )—
k-2
я=
1 ( l - ^ = p ) • Величины независимы,
в) Р (0 1 = ^1>
6g = i2, •••» 0/ y = i V ) = 1/М * если
Ov различны.
3.29. Р (0 Х*=!*!, 02 = ^2» •••! ^n — ^n ) =
_______________________
Pfa
P
i s
V 1 — Pit 1 — />«1 “ />£.'' " *1 — P i — •••— PiN - i '
3.30. а) М ( Л / - М ) В Д [Н 11;
б) A f»i (AI — M ) t e + l*/№k+l + 2h
в) Ml (W — M)\/N\, если 6t + 62+ . . . + k M +1= N — M .
_
3.31.
1+ F ( x t y )—
lim
(F {x t z) + F ( z t y)).
3.33.
Z - * + OO
Y p il
£
1 — }/~ 2 /2 = 0 ,2 9 2 8 9 ... 3.39. a) 1/2; 6) 2 b e - 2« (t > 0 ); в) 1/2.
P (Ai) = ni/n, i = l , 2, 3. 3.42. a) F|(1) (x) = l — (1 — F (*))";
3.34.
8.40.
6>
W = f " W!
B> %>?<«> (* b * 2) = ^ " ( * t ) - ( F (*2) - F fa ))» ,
ЛГ1^ *2-
6)
(A— 1)1 (m — ft— 1)! (n — m)l F* ~ l (* l ) X
X tF (x 2) — F (jcj)]ot —* —1 (1 — F (x2))n_m p (Xj) p (x2) f a < x 2).
3.44. l / ( f t + 1). 3.45. /1! p f a ) p f a ) . . .p (xn), если X !< x 2 sS ...sC x„,
и 0 в остальных случаях. 3.51. 4/ 2 < Р
1 < <j- < ; 4t (1 — t)
при 0 < < < 1 / 2 . 3.52. F _ , (l — l / V rl ) < m s < / :' _ i ( l / l / ^ ) ,
где
F _ ! (р) = sup {*: F ( x ) < у). 3.61. М£х = М |2 = 0, D|1= D |2 = l/2 ,
cov (|1( |2) = 0.
3.62. М'П1 = М % = 0; cov f a , т)2) = 0; случай-
2
ные величины зависимы. 3.63. М£ = -^R>
R2
D| = -jg -.3 .6 4 .M S „ = 0 ,
DS„ = n /2. 3.65. М Я „ = 0, D tf„ = l, « S 3 2. 3.66. a) M£ = D£ = X.,
M £ t* l= X * ; 6) M| = « p , D%= npq, M|f*J = n «J p * . 3.67. x«/nl
204
205.
3.68. e = 2,7 1 8 2 8 ...3.69.
cA= 1/(Ахт1). гдеЯ = l / a f + . . . + l / o £ ;
D r}„= 1A . 3.70. a) 0 ,9 9 7 3 0 ...; 6) 0 ,9 8 1 6 8 ...; в) 1; г) 8 /9 = 0 ,8 8 8 8 8 .. . ;
д) 0,9 139 3... 3.71. (Oi— a2) 2 « D (| + r )) < ( а ^ с г а ) 2. 8.72. М ? „ = и а ,
MLn — пра,
3.73.
D?„ = ncr2,
D£n = np (a2+ e 2?)i
D ^ J g . |Д
M C = J L ,
(1 + 6 | ) - 1 .
= MA2 = n\ o 2n. 3.76. M sin | > 0, M cos
Qjy
cov (£„, £^) = npo2.
8.74.
МД = 0, DA =
> 0. 3.77. max { p %1— p }.
OQ
3.78.
a) 2 g f f _ 64 = ~ 0 ,
300137.. . j
6) - 1 / 2 .
3.80.
l/(pq). 8.81. M 0 , = l / r , r g s l; D O ^ l . 8.82. 2
3.79.
6) l/( p 9).
N
( M — M k)™ /MM,
A=1
T ffiM = * M 1+ . . . + M i f . 3.88.
/V— n
D| = n - ^ - ( l —
.
...
/V— /И
x дг_ 1 • 3-84* Ж +Т (/==I'
^
Ж + Г (t==iM + l)-
3.85.
N + 1.
=
. . . ,.
М ц0 (« . N) = N ^ 1 — ^ - ) " = / V e - a (l + o ( 1)),
<"> m - s - ( i - ^ ) n+ n ( . - 4 ) * ( , - N ( i - ^ ) " ) _
=e/Ve~a (1 — (1 -(-a ) e ~ a) (1 + o ( 1)), п / ы —+ а , M —+ oo.
1 125
3 -3 6 - 1514 =
8 .8 7 .
^1—
1 Ы 0 25
I I 25 /
1 125\
1 ,3 6 2 9 1 ..., i - _ + j _ ( l _ ^ J = 0
f8 8 3 0 8 8 ...
— ►Я* п р и - — — In N — ►l n - j - . W — ► oo.
3.88.
AA.. _ A 7 / - X - 2
ir>H~ 1
M | X r — N C n + п - r - 2 / CN+ n - l
_
^
rtm Wf21
n
1)Гг H-13
A7
аГ
^ (оь_j_ 1) r + l
N
3.89. a) npi\ 6) npi (1 — pi)\ в)
npiPj. 3.90. a) 2
/=1
б)
| c M ( l - P/) » - ', B) N ^ l — L y .
M l. M v ,_ » £ У
- ( , D » ._ * F ^ Т Т + л Г '
/=о
M v jv = ( l + o ( l) ) .V ln .V
/=0
( N — *oo)
(\ — p ;) n\
206.
3.93. п {р [(1 - P j ) (1 - р а) а — (1 — (1 — Pi) (1 - Р а)) с ] — q [a ia 2b + ( l — « 1«г) с]}.3.94.
M ii1 = M % = 0 ,1 2 3 5 5 .. .,
0 % = 0 ,4 7 8 9 4 6 ...,
Dt]2 =
= 0 ,1 0 9 4 8 7 ..., D%/Dna= 4 ,3 7 4 3 7 ... 3.95. а) М l „ j = npu D | „,,-=
— п р ; ( 1 — р {), P ( l „ , e S* 1 ) = 1 — (1 — РвУ1', 6) M | n, i — npi, D % i,i=
=rn pt (l-p i),
P(|n, e^ l ) = l - ( 1 - P e ) m. где р 1 ~ С в
сС Ъ Ч с 1 9.
8 .9 6 . M i = n . 3 . 9 7 .1 + I^ l 2 . 3 . 9 8 . ^ T ( l - ( 4 ) " +1) . 3 . 9 9 . ^ .
3.100. M p0o = nq2 ( 1+ 0 ( 1)), Dp0o = npq* (1 + 3 q) ( l + o ( l ) ) , n — ►op.
3.101. Мр.ш = пр3 (1 + o (1)), Dp,1i1 — np3q (1 + 3 p + 5 p 2) (1 + o (1)),
П
n — ►oo. 3.102. a) qn\ 6) ^
(n—ft+ 1 ) pbqn~ k = —
(n9n(9_ p ) _
— p { q n— pn)) при q ф p, С2+12 ~ л при p= < ? = 1/2;
в) n p q + p *,
r) p q ( l — 3pq). 3.103. 155.
3.104.
pi (x) = i CnX1-1 (1 — х)п~ { ,
LL'tk __ (* + &--- l ) f^
— (n + k)m
гчб . _
8.105. Если 1 < t < / < n ,
Y 'iJn-i + f)
P <!</,. i</,) =
i
----^ + 0
**(я- j - (я + 2 ) 9
c o v (!<„. iy ,) = _ i g j ^ ± | L t
to
И „ I”1-
P (la )' l(/>) = °
при
lim min ( 4 - , ” - ' + j W
Я •+ оо
\/
Я— I -}- 1 J
8.110. a) M r| j= 1/n; 6) p(r|*, 4 ,) = -
— -
B ) p ( r i i + . . . + r ) ft,r ) ,+ . . . + % ) =
') ( n — ft) ’ К Ь < 1 < п .
Y
(ft Ф At
3.111. Координата b точки В — медиана распределения £, т. е.
Р (I < Ь) = Р (£ > Ь) = 1/ 2 . 3.112. д:— медиана £, г/— медиана г], т. е.
Р ( ? < * ) = Р (6 > х ) = ? (г] < у ) —? (г) > г/)= 1 / 2. 3.1 13.min М (£—я)2=
*
= D£ = M ( £ — М £)2. 3.128. а), б)
число из [0, а] при а < 1; любое
3.130. 1 / 3 < М £ < 2 / 3 .
Любое число из(0, 1]; в) любое
число из [1 — 1/а, 1] при а > 1.
F - i (а)
3.131.
a F _ x (a )—
00
+
5
^
F (л;) dx <
м£% ^
a F _ i (1 — а) +
—оо
(1 — F ( x ))d x ,
где F _ ! (t/) = sup {х:
F (х )« £ у}; мини-
F- 1 О -а )
Нальное значение М|х достигается при { х = 1} = { | < F _ i (a)},
а максимальное— при { х = 1} = { | ^ F _ i ( 1— a)}.
8.132.
206
Y
p ( l _ l ^ ^ c M
i < l + p ( l — | V ~ 2p )i
207.
экстремальные значения достигаются при< - 1 + V~p\ и
3.133. а) р/(1 + <
7 ); б), в) q/(l +
— *1 <
q);
г) (l + q ) £ q k - l ( l - q k - 1)
д)
{х = 1} =
=
(1 + ? ) р(, » ( * - »
е) р ( 1 +
(* = 2 ,3 , ...);
( f t = l , 2, 3, . . . ) !
( f t = i , 2, . . . ) ;
ж) 1/(1— 1)
1);
з) //2 .
3.134. а) 1/г ( 0 < x < z ) , 0 (х (£ [0, г]); б) 1/г ( O s s x s S z ) ,
если
0< г< 1,
1/(2— г)
( г— 1 < x < 1 ) ,
если
1<г<2;
в) 6 х (г — х ) / 2» ( 0 < К г ) . 3.135. а) г 2/12; б) г2/12 при 0 < г < 1 ,
(2 — г)2/ 12 при К г « £ 2 ; в) г2/20. 3.136. М (| || + t j = 2) = */2,
если
Р(1+т1=г) >0 или плотность р|+т) (г) >0.
^
^1+ »**+
Я ч + ...+ \ л г *
8.138.
Р ( l = m) = Cr%l Cr} f Z M l CN - 3-139- Стандартное нормаль
ное распределение.
3.140. F (х2) F (хз), где F (* ) = 0 при х * ^ г ,
F (*)= = m in
l|
(* S s z ).
3.141.
1+
1/2 +
. . . + 1/п.
3.142. Мт = a b , Dx=/>a2+ a 262. 3.144. Mvoo = (1 + ?)/<?2. Mvoo = 6
при р = 1/2. 3.145. Mvl u = ( l + p - | - p 2)/p3, M v x u = 14 при р = 1/2.
3.146. Mvoi = 1/(рр), Mvoi = 4 при р = 1/2. 8.147. пхп ~1.
3.148. 1— п21~ п. 3.149. Mv = 5, Dv = 4. 3.150. 1— n3~n+ 1.
3.151.
Р (I > х) = ( 1— 2^7 ) "
1
(0 < * < 2 nr),
Mg = — ■ ,
- ( т г У - 5 т '• '•«*• ' (Ь > *. Ь > . ) - ( I
0 < х , «/, х - \ - у < 2 п г , р = — 1/(/г— 1).
3.153.
Р (li > дг,
U
> X k> = ( l- X l + 2пг+ Х к ) П ~ 13
* / ^ 0 , X i -\-. . . + *£ =^2яг.
3.155. Mv = n ^1 — 2 ^ г у , - 1 = я е - г1А (1 + о (1 )),
D v = гее-^д (1 — (1 + А.2Д2) е-^ Д ) (1 + о (1)).
8.156.
Р (т ъ < * ) = ] £ ( - l ) * c 5 ( l — | М " ~ \
где х ^ О
к—О
и ( « ) + = т а х (а, 0). 3.157.
£
- i - _ ( i _ j _ 0 (1)) ^
1п п, п -* е е .
А=1
207
208.
3.158.M S = 3/(2я) = 0 ,4 7 7 4 ...,
M/> = 12/я = 3 ,8 1 9 7 ...,
М г = 1 2 /я а — 1 = 0 ,2 1 5 8 ...
3.161. P (| i |< 0 , 7 ) = 0 ,5 1 6 0 ... > P (| i| Ss 0,7) = 0 ,4 8 3 9 ...
3.162. P (— 0 , 5 < £ < — 0 ,l) = 0,1616... > P (I < | < 2) = 0 ,1 3 5 9 ...
8.168. M |a* “ 1 = 0, M|aft = 1 •3*5-...»(2ft— 1) a 2ft= (2ft— 1)!! a aft,
ft-=l, 2, ...
_ (In x - a f
x_
8 .1 6 5 .a )
i= r e
a V 2nx
-17==-e
a° 3 , * > 0; 6)
a(j3
,
o x Y 2k
x > 0.
3.166. Mg = / + 2 , D§ = e2a+G* ( e G * — l) . 8.167. а )2 Ф 0 (5/3) =
= 0 ,9 0 4 4 ... в любом случае; б) Ф (1 ,6 2 6 8 ...)— Ф ( — 1 ,7 1 6 ...) =
« 0 , 9 0 5 0 . . . при т = 60, Ф ( 1 ,5 2 7 ...) — Ф (— 2 ,2 1 4 .. .) = 0,9233...
ak +-i- <J2fe2
при m = 1 0 .
3.168. Mt]i = 1 »3*5 «, . ,* (2k— 1), Mr]\ = е
2
8.169. 0. 3.170. М cos g = e “ 1/a = 0,6065..., D cos| = y (1 — е~ *)а =
= 0 ,1 9 9 7 ...
3.171.
D sin | = - i ( l — е~ а) = 0 ,4 3 2 3 ... > D c o s g =
= . 1 ( 1 — e - i ) a= 0 , 1 9 9 7 ..,
3.172. М cos (£а) = у 1 / Г / 2 + 1 = 0 , 7 7 6 8 8 . .
М sin (|а) = 1 у Г У ~ 2 — 1 = 0 ,3 2 1 7 9 ...
3.173.
8.176.
а)
Являются.
3.174. а)
4Фо (1) = 0 ,4 6 6 0 ,..;
Нормальное;
б)
б)
нет.
8.175.
I.
2Ф0 (1) Ф0 (2) = 0 ,3 2 5 8 0 ...{
Э) Ф а (2) = 0 ,2 2 7 7 ...; г) 2Ф? (1 ) = 0,2330...; д) 1— e " 1/ 8 = 0 ,3 9 3 4 ...;
е) 1 — в " 1 = 0 ,6 3 2 1 ... 3.177. а) 4 Ф „(2,5) Ф0 ( 1) = 0,67420..
б)
2Ф0 (2,5) Ф0 (2) = 0 ,4 7 1 3 2 ...;
в)
[Ф0 (1,5) + Ф0 (0,5)1 X
Х [Ф „ (3) + Фо (2 )1 = 0 ,6 0 9 5 9 ...
, , 78.
= 0 ,0 8 4 9 4 ...
3.179. а) Ф§ ( V 2 ) / 2 = 0 ,0 8 8 7 6 .,.;
б) (Фо (2) — Фо ( V~~2)) — 0 ,0 5 0 2 3 ...;
в) (Ф а (2) — Фо ( У ~ 2 ))/ 2 = 0 ,0 2 5 1 1 ...
3.180. г е ~ г*12 /2 я (r S sO , 0 < ф < 2 я ) , 0 в остальных случаях.
8.181.
а)
2 2 Фо(3) = 0 ,9 9 4 6 0 ...;
в) 1— е - » = 0 ,9 9 9 8 7 ...
203
б)
1— е " 9/а = 0 ,9 8 8 8 9 ..
209.
3.182.а) в - * — e _ e /s = 0 ,1 2 4 2 ...t
б) 4 (ф* (3) — Ф? (2)) = 0,0 835 ^ ..;
й
4 ( ф: ( 4 5 ) _ ф ! ( - Р ) ) , 0 , , 0 5 4 . . .
3.184. poo =
PiI=
- J + 2~ arosin р, P o i = Рю = - j — ^
где р = - ■■r 2 i l = - — коэффициент корреляции
arcsin р,
и 5а* 3.185. 16.
V а11а22
3.186. in М || i . . . 1к |. 3.187. Мт|6= (0, 0, . . . , 0), cov (rfo , t\l/) = a y .
Глава
4
4 .2 . p j
Ь _ 3 .5 | > ,} < Ь р .
4 .3 . P J 3 L - p . | > , \ <
\
n
I
I
4.4. Выполняется.
4.7. а ^ О ,
1.
4.23. б) (1 — р ) р К
> H l_ t - W
4.5.
4.8.
Удовлетворяют.
Удовлетворяют.
4.24. Р ( п (N) > п) = Д
где
б (А£) = 1
при
- a .
n&2
4.6. ( К а < 1 .
4.16.
Всегда.
( 1— J E T * ) » °* М = 1 - * " * *
нечетном
N
и
6(Л0 = 0
при
четном
Ы9
G2 (*) = l - e - xS^ .
4.25. lim Р { % < * } = *, 0 ^ х ^ 1.
П —► оо
4.27.
Распределение Коши с параметром I. 4.28. Распределе
ние Коши с параметром 1.
4.29.
lim
X
Р { ( £ — x ) x s S y | l > * } = 1— е ~ ^ а\ у ^ О .
оо
4.30. a)
lim
п
б)
lim
Р
/z_ 1/ a C A :} = e " *
a (х > 0)i
оо
Р {хп П1^ ^ х\ = е “ (~ *)СХ (х < 0)?
П _>■ оо
в)
lim
Р {х п— In я ^ х} = е ~ е ~ х .
п -*• оо
4.37.
lim
П
Р { £ „ « ^ л ;} = 1— е ~ х , О С л: < оо. 4 .3 8 .а)
Dtfc = £a2. 4.39. Mx = aMv, Р | д^г ^
Dt^
=
оо
a2p + a 2^
3----- »
q2
f
6)
Тя
^^
а) ^ т<7
*
1
lim p 1"П— ^ x > = 1 — e ~ x ,
q-+ 0
j
O c * < oo.
209
210.
4.42. qHm P{<7TiCa:}=q ->lim
P{<7t2«^x} = 1— в x^at
-* 0
0
4.43. P
x^O .
*1—е~* 0<*<co. 4.44. 0,265. 4.47. a),
б) Сходится. 4.48. Равенство верно. 4.49. 6) Mg = 1 / 2 , Dg = 7/44.
4.50.
6) M g = 1/3, D | = 1/18.
4.51. F (x).
4.52. F ( ( /f t b e ) , если
k нечетное и у = У k\x — точка непрерывности F (у)\ F ( У k\x) —
- F i - V T x ) , если k четное,
и i/i, 2= ± У Т \ X— точки
непрерывности F (у). 4.53. Условия в). 4.54. а) Любое соотноше
ние может выполняться, б) m = m00. 4.55. а) М
М то; б) а 2^сг1>.
4.56. а) вЯ,(2- 1); б) р/(1 — qz)\ в) ( p z + q ) “ . 4.57. ф (z) = (pz + q)ni
M iП*=пр, M i W = n w p k, D ln = n p q , где <7 = 1 — p.4.59. Мтх = l / p f
D ti = qlp2,
MzTl =
• 4.60.
4.61.
M
= CT-i1PmQl ~ mi
1)
* /p ,
f y /p 2; 2)
| ~ , D E = -^ f.
m = m i + m 2+ m 3y
4.62.
l^ m .
4.63.
P{r] = / > =
a)
б) Kp, %p. 4.64. a) ix и i 2 распределены по закону Пуассона с
параметрами А, ( 1— р 2) и А ( 1— р г) соответственно; б) Mix = D ix =
= А,(1— р2), M i2 = D i2 = X (1 — рх), c o v (ix , i 2) = 0. Случайные
величины ix и i 2 зависимы.
4.66. а) (р1г1+ . . . + p N zN )n\ б) n W p f ,
nik+n р\ pj {i ф /).
4.67. MzVi гV 2гV «-(PA+fo+p,) г2+р4г3)",
M z ^ z f ” - 2Zg«- 3 = (PiZ1+ / > 2z1z2+ p 3z2zij- f.p 4Z3)n,
л/п
Р(Л«,г. пЛ»,*)^——
p (£
£
” ’ 1’
1
У/
(1_ Pl
pi)(i_p2_p3)P 2 — (P 1 +
)=
P 2) (P 2 + P 3)_____________
V ( P i + Р г ) (1 — P i — Рг) (P 2 + P 3) (• — P a— Р з )’
”’2
4.68.
4 .(59. « / 7 = a, p/Y= l —a — d,
6/y = — d, где O s ^ a ^ l , 0 ^ d < 1. 4.70. Все функции, кроме
ф4 (z), являются производящими при любой производящей функ
ции ф (z) и а £ [0 , 1); ф4 (z) является производящей только при
ф (z) = const.
4.71.
ф|(ег‘*).
4.72.
а)
б)
в) j z ! jt / a • 4-73- (n-Ь*—1)Е*3сс-*. 4.74. Me«S=g (/(1)),
MsB = g (< p (S)).
4.75.
« ! + . . . + « „ = «,
k-l
4.76.
a)
fc" 1 2
/=o
4.77. 11/27, 1/9.
210
Pi = . . . = pm= p .
k-\
f(2jij/k);
6)
k~i ^
/=0
f {2njlk)e-™i™UK
211.
4.80.P < ^
PК
< ft/2} «5 (2 }Tp \ l - p ) ) " .
1
p ita
4.81. pq. 4.82. / > М О + ( 1 - р ) / « (0 1 (* = 0);
6 )2 £ (i-c o s
(M
0 ),
4 -85- a) ~ Щ Г
1 <f = 0);
в)
{1 ф 0 )>
Са = с с /я ,
1— ос| ^ |
0 (|^| > a - x>. 4.86. Является. 4.87. Явля
ется. 4.88. а), б) Является. 4.89. He следует. 4.90. Изменится,
4.92. Равенство верно, если М | | | < о о . 4.95. а), в), е), з)
Являются; б), г), д), ж) Нет.
4.96.
а) 1— е - * / 2 (х > 0),
б) (1 — 2it)rl2
1—
(1 - { - 4f a) r/ 4 ехР | 2 a r c t g 2# | ,
M ( X2)A= r ( r + 2) . . . ( r + 2f e - 2).
4-97- ( T ^ = (T + l r / 2etaarCtg' ’
1).
4.98. Нормальное
распределение,
М£ = (а, с), D£ = (с, до).
4.99. Многомерное нормальное распределение в R m с вектором
математических ожиданий Са и матрицей ковариаций СВСТ, где
Т — знак транспонирования. 4.101.
4.110.
к™
т — 0, 1
М (|Х,- (я, /У,
С< " ~fe) ? . Функция f { (и)=
От
= M fx/(лг,
s) при любом t = 0, 1, . . . , s имеет единственный
максимум в точке tiQ= Nt и монотонна слева и справа от л0.
При фиксированных i n s
lim -мтах /г(п) = С‘ - ■
ЛМ-оо 'v
n
b
k N
4ЛП- p r X ( - D n - k c r - U c i r c l A s .
C N s m = fe
4.113. M|Ar (и, N) = C[l (N — 1 ) « - г/У -» + 1 .
4.114.
lim p i Vf ^ w < x l = l — е - ^ г/н (x3& 0).
w->® \ л7<г-1>/г
f
4.115. Распределение произведения
где случайные вели
чины
и £3 независимы и имеют распределение Пуассона
раметром К. 4.116.
790. 4.117. (— 7 4 ,3 6 < 1 0 -«# 74,36*10-"*).
N
/ N
4.118. б) Ф (х). 4.119.Ф (* ). 4.120. п 2 a iPi* я ( 2
i— 1
\ te l
с па
/ А,
—( 2
\2\
aFPi ) ) >
стандартное
нормальное
распределение.
211
212.
4.121.a)
MT]fc = 30f
Dr\k*=3b2,
cov (г)*,
г)г) = 0
(\k— / | ^ 3 ) ,
cov (rift, % + 2 ) = 6e. C O V (lift, T)*+1) = 262; б) Ф ( х / / " 3 ) . 4.122. Ф (x).
4.123.
a) x = p/( 1— p). 4.125. Стандартное нормальное распреде
ление. 4.126. М£<и> = 0, Dg(rt) = i ; ПрИ п — ^ w распределение цп
сходится к стандартному нормальному распределению. 4.127. При
п — *о распределение ч\п сходится к распределению разности
двух независимых целочисленных случайных величин, каждая из
которых имеет распределение Пуассона с параметром 1/ 2:
оо
ton Р { % - * } - в
2|fc| + am ml (\k \+m)\'
4.128.
F n ( x ) — > а + ( 1 — а) (1 — е ~ тх)
1 — dnA n — > т £ ( 0, оо), ап — > а< ^ \ при п — >-оо.
4.132. a) MsT« e s ^ l —
Р { т и > v ft- v z} = * ( ^ l )
П
(х ^ О ),
s j ^1 —
s) ’
{ ( 1_ ж
) / ( 1- 5
- ^
если
) } ;
б) 2 - Л
4.133. Распределение Пуассона e параметром %12.
4.134. М ги = ( 1 + о ( 1 ) ) Л П п ^ = Л
^-о+.охл-О^-Шу^),
стандартное нормальное распределение.
4.135. е - е ^ * в . 4.138.
Распределение
Коши
пр (0). 4.139. MeW(S‘ + b > = M e W(g‘ + *», = e -2 a | 4
с параметром
4.140. 1л.ь(х\ —
(д -}- 5) л
= аЬ {(а + Ь )2+ х * у
Глава
5.1.
5
1) (0,385, 0,836, 0,279); 2) 0,0336; 3) (16/47, 17/47, 14/47).
/4 /7
5-2- (Т/11
4 /7
\
t + m
10/11 ) * *'*’ ^ {r\t — m} = Ct
t +m
Р *
* ~ т
Я *,
если
t — т четно, Р{т]* = /п} = 0, если t — т нечетно.
5.4. 1) Нет, если р Ф q, да, если p = q = 1/ 2;2)
p ( m + i = i 1% = 0 = р .
р ( % + 1 = 1 l % = — i ) = i — р;
Р ц = РаЗ = Рз1 = Р 4 3 = 1
Р , P12 = P 24= = P82 = P44 = P-
5.5. Р (p 0 ( « + l ) = fe| Ho(n) = fe) = ft/lV,
Р(|х0 (/г + 1 ) = Й— 1 | \i0 (n) = k) = ( N - k ) / N .
6 .6 . Р (ц 0 ( « + 1) = k - l \ V L 0 (n) = k) = C % -lC ‘N _ k/C%.
212
да,
з)
да,
213.
5.9.Является.
5.10.
1/6.
lim Р (т„ > хп/а) — е ~ к4
3.12.
п-+ оо
х > 0. 5.13. 1; 4; 9. 5.16. Jt^> = (1 — Я,Л)/(1 — KN ) при р Ф qt где
K = q/p; n ^
l
e
= k/N при p = q = 1/2, я^0) = 1 — л ^ \ k = 0 t \, . . . t N.
n Л 43
171
86 \
оч оч П 5
! ) (^ 40 0’ 4 0 0 ’ 400 j ’
i qo
8 \
со
6 )^ = 1 ,4 2 2 6 8 ...;
p<£> =
18
* \ 4 l ’ 4 1 ’ 41 j '
)(
40
в) p < « > = ^ = 0 , 5 3 6 0 . . . ,
1— p<“ >, j = 1, 2;
г)
p < « > = ^ = 0 ,4 1 2 3 ..
92
я1= я 2= 0,
я3= 2 ^ = 0 ,3 1 6 1 ...}
Я 4=Ш = 0 ’ 1580" - ’ % = " 6 = ^ = 0 , 2 6 2 8 ...
5.23.
(Pu(t)
PiaWV
1
W (0
Рм (0 /
«4-pip
fP
I P —« — P)*/’ a
« у "1"
P
<*+P
~“\.
V“ P
Р/
,
Я1—a + P ’ "2 —1—"i5.27.
He следует. 5.28. у et
Глава 6
6.1.
Ms2 = a 2; s2 — состоятельная оценка a 3. 6.2. Mmr — a rt
Dmr = 2 S £ Z ^ r = 2 E . 6.3. a* = ^ c ft*ft, где cft =
_
6.4.
6.8. £p*— Ma X
Является.
6.5. Ф (* ).
6.7. р * = р ,„ /п .
X j / " P" (1~ P*) . P* + «a ^
P*
(1
j
fffe
> гДе P* = Vn/n,
n
1 — Ф (Ha) =oc. 6. 12. A,* = — ^
x/j, оценка состоятельная и несме-
k —i
П
(
~
D ~ = ^ 2 . 6.14. а) a* = а,
арифметические
по
D6* = i - a|, Dc* = y
\—
1
*/г ) , М р — i ,
= 6, с * = с , где а, Ь, с
соответствующим
выборкам;
ст|; 6) a * * = T (1 — k\) +
—
средние
Da* = -^-o'2,
(с— a) kl,
b** =
c**
= b ( l - k b ) + (c— b )k l ,
= c (l — kl) + ( a + b ) k l где 0 2 = a j +
+ 0i + a “, kl = a a
2/a\ Ь2
ь = 4 / о \ ^ = а?/ст2; Da** = a J (l — *J) / я ,
213
214.
Dfe** = <J* ( l — kl)/n, Dc** = o? ( \ - k c2)ln. 6.15.Г-
b*
- ,
6* 1
N — “ a - p y , П +И а-p — J ,
<*1
*=
’
+ 0^ 2
1 — Ф (м а ) = « .
f= = 1 ’ 2 ’ DA* = " J T
ci
Z l + 22 + ( * + P ) *3
3+ p
B)
где
_
*
Z = C i Z 1+ C 222+ y
28>
1=1
6.16. c; =
-2 + V 2g 3- 6.17. а) z =
+ a 2
1+ P e
зЦ _p »
6) z — (zx+ z2)/2,
Dz = 1 /2 .
c 1 + c 2= - i - ;
- ( g
= j-L -£
« * = /., w
Dz = 0;
6 .1 8 .
- ?
Л* =
( i л а ) ' 1.
где n = n1+ / t 2+ . . . + n ft.
6.19. См. ответ к задаче 6.18.
6.20. М г|„=1/Л/, Dr)„ =
= 2/ ( a W ) + 0 (l/W<!)>n / l V - * a 1 Af- х » . a = const.
0 .21. Щ , - , „ + ± = ± .
,
1 -;» Л
1
^
6.22. Mx(1) = — , D^(i)
1
. Mx(») = ^ X
П
T ’
DX(n) :
k=l
^
1* - cov (*««• *<«>)
•6-23- а) M0^= M02
k-1
rvQ* _
(&— a ) 2
1
12n
ГЧД*
’
(6 — a ) 2
002 - 2 T n + l ) ( n + 2) ’
M 02=2 4 ( 1 + T +
1
1
.
r ,o * _
6) M01
+ T ^ Z T ) + 4 ) - D02 = 4 ^ ( 1+ i +
4 \
+ з * - •- + ( Н = 1 ) 5 +
£
П
й *)* 6-24- Mc* = c - Dc* =
Pk0)
6.28. % = / .
*n —(1 7 » гДе \k — число
k= i
1
a ’ 001
i •6-27-
k = i
**
исходов с номером k.
Pk
6.29. a) С = ticlq-J—Ucx,Gq ]/ ti\ 6) Ucc®o~^~
l ==(^i— ^o)
®) 0*
l
6.30. a0 = e - V , аг = ^ е - У ё < хЫх.
1
6.31
.31. a? = ^
о
214
1
/ 1
42
<*) d x — ^ e ~ 2V&w dx— y ( f S(x) в~У^(хЫх j
о
\ о
/
215.
N 05 ^05 со ^
n - см
Ю Ю ^
23 ------ 1 ю оо см
03
О
о
N
O J ^ O in
00 CM 00 —x
^
00 СО оо о
о"
lO
00 CO N
^ со о co
lO C O N S
CO ^
429
o '
823
517
TjH 00 05 ю
со о см см
CM I O N 05
CO
0 ,2 1 9 0
05 00 Ю
00 О 05
00 N- 05
306
418
406
o '
05 *-« 05 ^
00 00 r f
C M lflN C )
0 ,4 1 6 2
о
0 ,3 1 0 6
^ CM ^ CM
00 00 CO CO
^ Ю CO N
0 ,3 0 7 8
см со о
00 00 N
о CM CO
0 ,3 0 5 1
O O lflO O N
со оо о о
CM ^ N- 05
сол
0 ,3 0 2 3
СО ^ 05 N- 00 N05 СО —< Ю N СО
00 СО 05
0 3 со о
—
см
ю ^ о см
ю N . со
С О Ю Ь 05
422
Ю *—<«
—<00
05 05 N . co
^ Ю CO N .
844
10 05 0 0 ^
O O N ^
Ю Ю CD N
о n -о о
Tt< N . 05 00
00 Ю N 05
0 ,2 0 8 8
t o оо со о
— • о оо ю
Ю COCO N
Ю 05 О N
СО 05 -Ч 05
со ю оо 05
0 ,2 0 5 4
JO 00 CO
- '1 — <05 Ю
Ю CO C O N
394
CD
382
о
05
im r . j ) * 4
CO CM 05 cO
ю с о с о ь
480
714
05 см оо
^ Ю 00
ю о о -н
00
а
ха
к
S
О 00 СМ
^ сосо
О ^ 00
<3
N. - « о
^ 0 5 10
CM LO 05
о
о*
0 ,4 1 4 7
292
279
0 ,4 1 3 1
0 ,4 1 1 5
265
251
05 N- Ю
О ^
О CM co
CO
O ' 05
CO CO
—<
^ Ю CO N
o '
cd
CD
o~
222
CO N- Ю 05
00 CO CO CO
—<
CO oo
CO
939
s = s
CM СО 05
CM
642
CO CO CO
N- N- Ю CM
TJH ю CO N
0 ,4 0 6 6
o '
см — со oo
-4 CO 00 00
CM ^ CO oo
CO
0 ,4 0 9 9
794
486
454
764
734
0 ,2 1 5 7
0 ,2 1 2 3
443
808
772
406
0 ,1 3 6 8
736
700
0 ,1 3 3 1
675
0 ,1 0 6 4
0 ,1 0 2 6
0 ,0 2 3 9
636
596
0 ,0 2 0 0
987
948
910
871
ю оо ю
ю см оо
СМ СО 05
357
S
S
0 ,0 1 2 0
0 ,0 1 6 0
<N
сГ
0 ,2 3 2 4
©
со
0 ,0 0 8 0
l(N
cT
332
05 CO CO 05
Ю
^
*-4 TjH CO 00
CM ^ ^ CO
Ю Ю \t< «4
^ in c o s
o '
05 о
СО ^ Ю
CO N 00 05
•b * ft *
192
881
580
0 ,2 2 5 7
915
554
0 ,1 1 7 9
793
О
398
93
СО
0 ,0 0 0 0
93
0 ,4 0 3 2
Т аблицы.
НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
а
к
<и
2
н
о
и
557
ю
517
to
478
N
0 ,0 2 7 9
!
00
о
0 ,0 3 1 9
о
0 ,1 Ю З
05
се
Cf
К
Ч
V?
К
о
оз
o ' сГ о"
CO N
00
А
О О О
00
А
О О О
215
216.
( продол жен ие)1.
Таблица
t— О СО CD са
rf —<со о
»-<юд>**-оо ю со оо со 05
000000 05 05 0 05 05 05 05 05
OJ
со
^ ю оо —1 со
0000000505
о
ю
о
о
ю
Ttl
1—100 00о ю
ю со t'- оо оо
о
о
05 05 05 05 05
о
о
ОС CM00 СО03 СО О О оо 'Ф 05
03 Tf Г'-. О CM Tti СО С^. 00 00
00 00 0505 05 05 05 05 05 05
СО ООЮ ^ Г^
05 00
05 (М
С^. 00 00 05 05
ОО T f
00 00
t"- 00
—«—* LO
с^.О СМ
0005 05
со о ос оо см
ОС СО СО 05 CM
00 00 00 05
Ю 05 0 5 N ^
тРЮ СО Г^ О О
05 05 05 05 05
00 Г"- ОС Г^. ОО
^ LO СО t^- 00
0505050505
<со
00
05
оо
о
00
о
о
оо
*
—1
ю
см
о
о
о
со
05
*
—ч
о
см
о
о
00
ю
о
см
ю
о
о
о
о
SJ
Я
»
00 СО со о
о ю сою см
С^.СМС005СМ Tf ю со с-- оо 00
00 00 ОО05 05 05 0505 05 05
05
я
я
оЕГ
<Я
я
С
М—^ 00 00 СО
ООСОЮ
^—
N (М СО 05 —
Ю СО N 00 00
СП
03
а
я
о —' см со ' f iocot>-ooo5 о
см"см см"см"см" см"см"см"см"см со
о?
о
н
й)
w
4
г
см
ч
ю
о
о
о
00
СО
см
00
см
ю
о
о
о
оо
ю
С"ю
см
о
о
г
о
см
о
05
о
00
8
а
5
о
оя
о
та
е
8
К
§я
п
>»
о
216
оо
S
S
0505050505
05
I(е.
к
00
00
05
я
00 0О 00 05
Ttl
03
со
ю
00
00
05
со см с^.
T f Ю СО
ОО
0505050505
СО
ю
ю
00
00 СО ' 05 —| 00—«—«0510 05
О Tf ООО 00 Tf СО
00 00
0000000505 05 05 05 05 05 05
5
Г"о
t"-
о
о
о
ООО Tf —•СМ 05 CMСМ05 Ю 05
О Ю 00 —СО Tf СО Г'- t"- 00 ОО
00 ОО ОО0505 05 05 05 05 05 05
05
8
217.
РАСПРЕДЕЛЕНИЕ ПУАССОНАТаблица
0
1
2
3
3.
Значения функции p k (k) =
№ в-а
0,1
0,2
0,3
0,4
0,6
0 ,9 0 4 8 4
0 ,0 9 0 4 8
0 ,0 0 4 5 2
0 ,0 0 0 1 5
0 ,8 1 8 7 3
0 ,1 6 3 7 5
0 ,0 1 6 3 8
0 ,0 0 1 0 9
0 ,0 0 0 0 6
0 ,7 4 0 8 2
0 ,2 2 2 2 5
0 ,0 3 3 3 4
0 ,0 0 3 3 3
0 ,0 0 0 2 5
0 ,6 7 0 3 2
0 ,2 6 8 1 3
0 ,0 5 3 6 3
0 ,0 0 7 1 5
0 ,0 0 0 7 2
0 ,0 0 0 0 6
0 ,6 0 6 5 3
0 ,3 0 3 2 7
0 ,0 7 5 8 2
0 ,0 1 2 6 4
0 ,0 0 1 5 8
0 ,0 0 0 1 6
4
5
0,00002
6
0
1
2
3
4
5
6
0,00001
0,6
0 ,7
0,8
0 ,9
0 ,5 4 8 8 1
0 ,3 2 9 2 9
0 ,0 9 8 7 9
0 ,0 1 9 7 6
0 ,0 0 2 9 6
0 ,0 0 0 3 6
0 ,0 0 0 0 4
0 ,4 9 6 5 9
0 ,3 4 7 6 1
0 ,1 2 1 6 6
0 ,0 2 8 3 9
0 ,0 0 4 9 7
0 ,0 0 0 7 0
0 ,0 0 0 0 8
0 ,4 4 9 3 3
0 ,3 5 9 4 6
0 ,1 4 3 7 9
0 ,0 3 8 3 4
0 ,0 0 7 6 7
0 ,0 0 1 2 3
0 ,0 0 0 1 6
0 ,4 0 6 5 7
0 ,3 6 5 9 1
0 ,1 6 4 6 6
0 ,0 4 9 4 0
0,00001
0,00002
0 ,0 0 0 3 0
0 ,0 0 0 0 4
7
0,01112
0,00200
1,0
2,0
3 ,0
4,0
5 ,0
7
0 ,3 6 7 8 8
0 ,3 6 7 8 8
0 ,1 8 3 9 4
0 ,0 6 1 3 1
0 ,0 1 5 3 3
0 ,0 0 3 0 7
0 ,0 0 0 5 1
0 ,0 0 0 0 7
8
0,00001
0 ,1 3 5 3 4
0 ,2 7 0 6 7
0 ,2 7 0 6 7
0 ,1 8 0 4 5
0 ,0 9 0 2 2
0 ,0 3 6 0 9
0 ,0 1 2 0 3
0 ,0 0 3 4 4
0 ,0 0 0 8 6
0 ,0 0 0 1 9
0 ,0 0 0 0 4
0 ,0 4 9 7 9
0 ,1 4 9 3 6
0 ,2 2 4 0 4
0 ,2 2 4 0 4
0 ,1 6 8 0 3
0 ,1 0 0 8 2
0 ,0 5 0 4 1
0 ,0 2 1 6 0
0 ,0 0 8 1 0
0 ,0 0 2 7 0
0 ,0 0 0 8 1
0,00001
О^00022
0 ,0 0 6 7 4
0 ,0 3 3 6 9
0 ,0 8 4 2 2
0 ,1 4 0 3 7
0 ,1 7 5 4 7
0 ,1 7 5 4 7
0 ,1 4 6 2 2
0 ,1 0 4 4 5
0 ,0 6 5 2 8
0 ,0 3 6 2 7
0 ,0 1 8 1 3
0 ,0 0 8 2 4
0 ,0 0 3 4 3
0 ,0 0 1 3 2
0 ,0 0 0 4 7
0 ,0 0 0 1 6
0 ,0 0 0 0 5
0
1
12
0 ,0 0 0 0 6
0 ,0 1 8 3 2
0 ,0 7 3 2 6
0 ,1 4 6 5 3
0 ,1 9 5 3 7
0 ,1 9 5 3 7
0 ,1 5 6 2 9
0 ,1 0 4 1 9
0 ,0 5 9 5 4
0 ,0 2 9 7 7
0 ,0 1 3 2 3
0 ,0 0 5 2 9
0 ,0 0 1 9 3
0 ,0 0 0 6 4
13
14
15
16
17
0-,00001
0,00020
2
3
4
5
6
9
10
11
0 ,0 0 0 0 6
0,00002
0,00001
2 if
218.
РАСПРЕДЕЛЕНИЕ СТЬЮДЕНТАТаблица
4. Значения функции i a , п
Функция taf n определяется равенством
Р {^п > ^а, п) = ос»
где случайная величина тп имеет распределение Стьюдента С п
степенями свободы. Плотность распределения тп равна
П+ 1
рХ „< Ф
21В
2
219.
/^РАСПРЕДЕЛЕНИЕТаблица
б.
Значения функции Ха,т
Функция
т определяется равенством
Р (Х/n^ Ха, т ) ==а*
где случайная величина х ^ имеет х 2‘ Распределение с т степенями
свободы. Плотность распределения х ^ равна
N.
Н
е
*
0
А
г (4 )
л*
2*
1
1
Р о М
Л/п
а
т
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
26
0 ,1 0
0*05
0 ,0 2
0,0 1
0 ,0 0 5
2,7
4,6
6,3
7 ,8
9,2
10,6
12,0
13,4
14,7
16,0
17,3
18,5
19,8
21,1
22,3
23,5
24,8
26,0
27,2
28,4
29,6
30,8
32,0
33,2
34,4
3,8
6 ,0
7 ,8
9 ,5
5 ,4
7 ,8
9 ,8
11,7
13,4
15,0
16,6
18,2
19,7
21,2
22,6
24,1
25,5
26,9
28,3
29,6
31,0
32,3
33,7
35,0
36,3
37,7
39,0
40,3
41,6
6,6
9 ,2
11,3
13,3
15,1
16,8
18,5
20,1
21,7
23,2
24,7
26,2
27,7
29,1
30,6
32,0
33,4
34,8
36,2
37,6
38,9
40,3
41,6
43,0
44,3
7 ,9
11,6
12,8
14,9
16,3
18,6
20,3
21,9
23,6
25 ,2
26,8
28,3
29,8
31
32,5
34
35,5
37
38,5
40
41,5
42,5
44,0
45,5
47
\
11,1
12,6
14,1
15,5
16,9
18,3
19,7
21,0
22,4
23,7
25,0
26,3
27,6
28,9
30,1
31,4
32,7
33,9
35,2
36,4
37,7
219
220.
РАВНОМЕРНО РАСПРЕДЕЛЕННЫЕ СЛУЧАЙНЫЕ ЧИСЛАТ а б л и ц а 6 . Приведенные в таблице цифры можно рассматри
вать как реализации независимых и одинаково распределенных
случайных величин, принимающих значения 0, 1,..., 9 с одной и
toft же вероятностью, равной 0,1
10
37
08
99
12
С9
54
42
01
80
73
20
26
90
79
25
48
89
25
99
33
05
53
29
70
76
64
19
09
80
52
89
64
37
15
01
47
50
67
73
35
42
93
07
61
86
96
03
15
47
34
24
23
38
64
67
80
20
31
03
35
52
90
13
23
48
40
25
11
66
76
37
60
65
53
80
20
15
88
98
95
63
95
67
95
90
61
33
67
11
91
04
47
43
68
17
02
64
97
77
39
00
35
04
12
29
82
08
43
17
27
29
03
62
17
49
16
36
76
68
45
65
06
59
33
66
31
85
63
73
06
06
26
57
79
57
01
97
33
64
47
08
76
21
57
17
05
02
35
53
34
45
02
05
03
07
57
05
32
52
27
18
16
54
96
68
24
56
70
47
50
06
92
48
78
36
35
68
90
35
69
30
66
55
80
73
34
57
35
83
61
26
48
75
42
70
14
18
48
82
65
86
73
28
60
81
79
05
46
93
33
90
38
82
52
98
74
52
87
03
85
39
47
09
44
11
23
18
83
35
19
40
62
49
27
92
30
38
12
38
91
97
85
56
84
70
32
79
24
35
98
11
83
88
99
52
80
45
68
59
01
50
29
54
46
77
54
96
02
73
67
31
34
00
48
14
39
06
86
87
90
80
28
50
51
56
82
89
75
76
86
77
80
84
49
07
32
83
01
69
22
50
13
36
91
10
72
74
76
82
94
56
67
66
60
05
82
00
79
89
58
48
78
51
28
60
29
18
90
93
97
40
47
36
78
09
52
54
47
56
34
42
06
64
13
33
01
10
93
68
50
52
68
29
23
50
77
71
60
47
07
56
17
91
83
39
78
78
10
41
98
51
17
62
13
65
80
74
69
09
48
12
35
91
89
11
43
09
62
32
76
56
98
68
05
74
35
17
03
05
17
17
77
66
14
46
72
40
25
22
85
70
27
22
56
09
80
72
91
85
50
15
14
48
14
58
45
43
36
46
04
31
23
93
42
77
82
60
68
75
69
23
02
72
67
74
74
10
03
88
73
21
45
76
96
03
И
52
62
29
95
57
16
11
77
71
82
42
39
88
86
53
37
90
22
40
14
96
94
54
21
38
28
40
38
81
55
60
05
21
65
37
26
64
45
44
63
55
18
98
91
80
44
12
63
49
33
10
55
60
91
69
48
07
64
45
45
19
37
93
23
98
49
42
29
68
26
85
И
16
47
94
15
10
50
92
03
74
00
53
76
68
79
20
44
86
58
54
40
84
46
70
32
12
40
16
29
97
86
21
28
73
92
07
95
35
41
65
46
25
54
35
75
97
63
94
53
57
96
43
75
14
60
64
65
08
03
04
48
17
99
33
08
94
70
23
40
81
39
82
220
221.
НОРМАЛЬНО РАСПРЕДЕЛЕННЫЕ СЛУЧАЙНЫЕ ЧИСЛАТ а б л и ц а 7. Приведенные в таблице 7 числа можно рассмат
ривать как реализации независимых нормально распределенных
величин с параметрами а = 0, сг = 1
0 ,4 6 4
0 ,0 6 0
1 ,4 8 6
1 ,0 2 2
0 ,3 9 4
0 ,1 3 7
2 ,4 5 5 — 0 ,3 2 3 — 0 ,0 6 8
0 ,2 9 6 — 0 ,2 8 8
1 ,2 9 8
— 2 ,2 5 6 - 0 , 5 3 1 — 0 ,1 9 4
0 ,1 8 7 — 1 ,1 9 0
0 ,5 4 3 — 1 ,5 5 8
- 0 , 3 5 4 — 0 ,6 3 4
0 ,6 9 7
0 ,9 2 6
1 ,3 7 5
0 ,7 8 5 — 0 ,9 6 3
— 0 ,4 7 2
0 ,5 7 1 — 1,8 51
1 ,2 7 9
3 ,5 2 1
0 ,1 9 4
1 ,1 9 2
— 0 ,5 5 5
0 ,0 4 6
2 ,9 4 5
1 ,9 7 4 — 0 ,2 5 8
0 ,3 2 1
0 ,4 1 2
0 ,9 0 6 — 0 ,5 1 3 — 0 ,5 2 5
0 ,5 9 5
1 ,5 7 9
0 ,8 8 1 — 0 ,9 3 4
0 ,1 6 1
1 ,1 7 9 — 1 ,0 5 5
0 ,0 0 7
0 ,7 6 9
0 ,9 7 1
0 ,7 1 2
1 ,0 9 0 — 0 ,6 3 1
— 1,501 — 0 ,4 8 8 — 0 ,1 6 2 — 0 ,1 3 6
1 ,0 3 3
0 ,2 0 3
0 ,4 4 8
0 ,7 4 8
-0 ,6 9 0
0 ,7 5 6 — 1 ,6 1 8 — 0 ,3 4 5 — 0 ,5 1 1 — 2 ,0 5 1 — 0 ,4 5 7 — 0 ,2 1 8
1 ,3 7 2
0 ,2 2 5
0 ,3 7 8
0 ,7 6 1
0 ,9 6 0 — 1 ,5 3 0
0 ,1 8 1 — 0 ,7 3 6
-0 ,4 8 2
1 ,6 7 8 — 0 ,0 5 7 — 1 ,2 2 9 — 0 ,4 8 6
0 ,8 5 6 — 0 ,4 9 1 — 1 ,9 8 3
- 1 , 3 7 6 — 0 ,1 5 0
1 ,3 5 6 — 0 ,5 6 1 — 0 ,2 5 6 — 0 ,2 1 2
0 ,7 7 9
0 ,2 1 9
-1 ,0 1 0
0 ,5 9 8 — 0 ,9 1 8
1 ,5 9 8
0 ,0 6 5
0 ,4 1 5 — 0 ,1 6 9
0 ,3 1 3
- 0 , 0 0 5 — 0 ,8 9 9
0 ,0 1 2 — 0 ,7 2 5
1 ,1 4 7 — 0 ,1 2 1
0 ,1 8 1
1 ,0 9 6
1 ,3 9 3 — 1 ,1 6 3 — 0 ,9 1 1
1,2 3 1 — 0 ,1 9 9 - 0 , 2 4 6
1 ,2 3 9 — 2 ,5 7 4
— 1 ,7 8 7 - 0 , 2 6 1
1 ,2 3 7
1 ,0 4 6 — 0 ,5 0 8
— 0 ,1 0 5 — 0 ,3 5 7 — 1 ,3 8 4
0 ,3 6 0 — 0 ,9 9 2
— 1 ,3 3 9
1 ,8 2 7 — 0 ,9 5 9
0 ,4 2 4
0 ,9 6 9
1,041
0 ,5 3 5
0 ,7 3 1
1 ,3 7 7
0 ,9 8 3
0 ,2 7 9 — 2 ,0 5 6
0 ,7 1 7 — 0 ,8 7 3 — 1 ,0 9 6
— 1 ,6 3 0 — 0 ,1 4 6 — 0 ,3 9 2
— 0 ,1 1 6 — 1 ,6 9 8 — 2 ,8 3 2
— 1,1 4 1 — 1,0 4 1
0 ,3 6 2
— 1 ,3 3 0
1 ,6 2 0 — 1 ,0 4 0
1,0 4 7
— 1 ,3 9 6
0 ,0 8 9
- 1 , 8 0 5 — 2 ,0 0 8 — 1 ,6 3 3
0 ,5 4 2
0 ,2 5 0 - 0 , 1 6 6
0 ,0 3 2
0 ,0 7 9
-1 ,1 8 6
1 ,1 8 0
1 ,1 1 4
0 ,8 8 2
1 ,2 6 5 — 0 ,2 0 2
0 ,1 5 1 — 0 ,3 7 6
0 ,6 5 8 — 1,141
1,1 51 — 1 ,2 1 0 — 0 ,9 2 7
0 ,4 2 5
0 ,2 9 0 — 0 ,9 0 2
— 0 ,4 3 9
0 ,3 5 8 — 1 ,9 3 9
0 ,8 9 1 — 0 ,2 2 7
0 ,6 0 2
0 ,8 7 3 — 0 ,4 3 7
— 1 ,3 9 9 — 0 ,2 3 0
0 ,3 8 5 — 0 ,6 4 9 — 0 ,5 7 7
0 ,2 3 7 — 0 ,2 8 9
0 ,5 1 3
0 ,1 9 9
0 ,2 0 8 — 1 ,0 8 3 — 0 ,2 1 9 — 0 ,2 9 1
1,2 21
1 ,1 1 9
0 ,1 5 9
0 ,2 7 2 — 0 ,3 1 3
0 ,0 8 4 — 2 ,8 2 8 — 0 ,4 3 9 — 0 ,7 9 2
2 ,2 7 3
0 ,6 0 6
0 ,6 0 6 — 0 ,7 4 7
0 ,2 4 7
1,2 91
0 ,0 6 3
0 ,0 4 1 — 0 ,3 0 7
0 ,7 9 0 — 0 ,5 8 4
0 ,1 2 1
0 ,5 4 1
0 ,4 8 4
- 1 , 1 3 2 — 2 ,0 9 8
0 ,9 2 1
0 ,1 4 5
0 ,4 4 6 - 1 , 6 6 1
1 ,0 4 5
0 ,0 0 4
— 1 ,2 7 5
— 1 ,7 9 3
— 0 ,9 8 6
— 1 ,3 6 3
0 ,7 6 8
0 ,0 7 9 — 1 ,4 7 3
0 ,0 3 4
0 ,3 7 5 — 1 ,6 5 8 — 0 ,8 5 1
0 ,2 3 4
- 0 , 5 1 3 — 0 ,3 4 4
0 ,2 1 0 — 0 ,7 3 6
0 ,2 9 2 — 0 ,5 2 1
1 ,2 6 6 — 1 ,2 0 6
1 ,0 2 6
2 ,9 9 0 - 0 , 5 7 4 — 0 ,4 9 1
— 0 ,8 8 0
— 0 ,1 5 8
— 0 ,8 3 1
— 0 ,8 1 3
— 1,3 4 5
— 2 ,1 2 7
— 0 ,6 5 6
1,0 4 1
— 0 ,8 9 9
-1 ,1 1 4
0 ,6 6 5
0 ,0 8 4
0 ,3 4 0 — 0 ,0 8 6
0 ,0 0 8
0 ,4 2 7
0 ,1 1 0 — 0 ,5 2 8
1 ,2 9 7 — 1 ,4 3 3
721
222.
Таблица— 1 ,3 3 4
1 ,2 7 8
— 0 ,2 8 7 — 0 ,1 4 4
0 ,1 6 1 — 0 ,8 8 6
— 1 ,3 4 6
0 ,1 9 3
1 ,2 5 0 — 0 ,1 9 9
7 (продолжение)
— 0 ,5 6 8 — 0 ,1 0 9 — 0 ,5 1 5 - 0 , 5 6 6
0 ,5 0 0
2 ,9 2 3
— 0 ,2 5 4
0 ,5 7 4 — 0 ,4 5 1 — 1 ,1 8 1 — 1 ,1 9 0 - 0 , 3 1 8
— 0 ,9 2 1 — 0 ,5 0 9
1 ,4 1 0 — 0 ,5 1 8
0 ,1 9 2 — 0 ,4 3 2
— 1 ,2 0 2
0 ,3 9 4 — 1 ,0 4 5
0 ,8 4 3
1 ,0 4 5
0 ,9 4 2
1 ,3 7 8
0 ,5 8 4
— 0 ,2 8 8
1 ,8 1 0
1 ,2 1 6
0 ,7 3 3
0,630 — 0,537
0,782
0,060
0,375 — 1,941
0,247 — 0,491
— 1,420
0,489 — 1,711 — 1,186
—0,151 — 0,243 — 0 ,430 - 0 , 7 6 2
— 0,309
0,531
0,416 — 1,541
0 ,4 9 9 - 0 , 4 3 1
1 ,7 0 5
1»164
0 ,6 6 5 — 0 ,1 3 5 - 0 , 1 4 5 - 0 , 4 9 8
0 ,7 5 4 - 0 , 7 3 2 - 0 , 0 6 6
1 ,0 0 6
0 ,2 9 8
1 ,0 4 9
1 ,8 1 0
2 ,8 8 5
1 ,4 5 6
2 ,0 4 0 — 0 ,1 2 4
0 ,1 9 6
0 ,4 8 4 — 1 ,2 7 2
0 ,1 1 6
0 ,4 2 4 — 0 ,4 4 4
0 ,5 9 3
0 ,9 9 3 — 0 ,1 0 6
0 ,5 9 3
0 ,6 5 8 — 1 ,1 2 7 — 1 ,4 0 7 - 1 , 5 7 9 — 1 ,6 1 6
1 ,2 6 2
1 ,4 5 8
0 ,5 3 2
0 ,8 6 2 — 0 .8 8 5 — 0 ,1 4 2 — 0 ,5 0 4
0 ,0 2 2 - 0 , 2 8 1
1,381
1 ,7 0 7
0 ,2 3 5 — 0 ,6 2 8 — 0 ,0 2 3 — 0 ,4 6 3 — 0 ,8 9 9 — 0 ,3 9 4 - 0 , 5 3 8
0 ,4 1 0 — 0 ,3 4 9 — 1 ,0 9 4
0 ,5 8 0
-0 ,8 5 3
0 ,4 0 2
0 ,7 7 7
0 ,8 3 3
0 ,2 4 1
0 ,0 2 2
— 0 ,8 5 3
— 0 ,5 0 1
0 ,4 3 9
— 0 ,9 5 7
0 ,5 2 5
— 1 ,8 6 5
— 0 ,2 7 3
— 0 ,0 3 5
0 ,4 7 1 — 1 ,0 2 9
— 0 ,3 1 0
0 ,4 7 9
0 ,6 1 0
2 ,7 0 9
— 0 ,2 2 0 — 0 ,0 5 7
0 ,7 3 8 — 0 ,3 0 0
— 1 ,8 8 5
0 ,3 7 1
— 0 ,2 5 5 — 0 ,7 0 2
— 0 ,4 2 3 — 0 ,4 3 2
0 ,8 5 7 - 0 , 4 6 5
— 0 ,2 6 0
0 ,1 2 0
— 2 ,0 1 5
— 0 ,6 2 3
— 0 ,6 9 9
0 ,4 8 1
— 0 ,5 8 6
— 0 ,5 9 4 — 0 ,5 7 9
— 1 ,0 4 7 — 0 ,1 2 0
0 ,1 9 1
— 1 ,3 4 7
0 ,0 7 1
0 ,9 9 6
— 1 ,0 2 3 — 3 ,0 0 1
0 ,8 8 4 — 0 ,2 9 8
1 ,0 6 6
1 ,0 9 7
0 ,4 5 7
1 ,0 6 4
0 ,7 3 6 — 0 ,9 1 6
— 0 ,7 9 8
0 ,1 6 2 — 0 ,3 4 2
1 ,2 2 2
— 0 ,7 6 8 — 0 ,1 2 9 — 0 ,1 8 8 — 1 ,1 5 3
0 ,0 2 3 — 1 ,2 0 4
1 ,3 9 5
1 ,2 9 8
1 ,5 3 1
0 ,3 4 9
— 0 ,4 4 3 — 0 ,2 9 2
1 ,4 0 9 — 0 ,8 8 3
1 ,7 3 0 — 0 ,0 5 6
— 0 ,2 6 6
0 ,7 5 7
— 2 ,8 3 0 — 0 ,2 3 8
0 ,9 5 3 — 0 ,8 6 9
— 0 ,9 7 3 — 1 ,0 1 6
— 1,6 91
0 ,4 1 7
-0 ,5 5 8
0 ,0 5 6
— 0 ,6 2 7
0 ,5 6 1
— 1 ,1 0 8 — 2 ,3 5 7
-1 ,7 2 6
1 ,9 5 6
0 ,5 2 4 — 0 ,2 8 1
-0 ,5 7 3
0 ,9 3 2
0 ,3 5 9
0 ,5 5 1
0 ,4 1 8 — 0 ,0 9 4
1,5 0 1
0 ,0 7 4
0 ,5 2 4
0 ,0 3 1
0 ,4 0 2
0 ,4 7 9
0 ,3 2 6
1 ,1 1 4
1 ,0 6 8
0 ,7 7 2
0 ,2 2 6
0 ,3 1 8
- 1 , 7 5 2 — 0 ,3 2 9 — 1 ,2 5 6
0 ,0 8 5
1,7 01 — 1 ,0 8 7
— 0 ,2 9 1
0 ,8 9 9
0 ,1 3 0
0 ,6 7 4
— 0 ,9 3 3
— 0 ,4 5 0 — 0 ,2 4 4
0 ,0 7 2
1 ,0 2 8
0 ,4 9 0 — 1 ,3 0 4
0 ,5 1 2 — 0 ,8 8 2
0 ,4 1 5 — 1 ,0 8 4 - 0 , 8 5 6
— 0 ,9 5 8 - 0 , 0 5 9
0 ,3 1 8 — 0 ,2 7 6
0 ,2 4 8 — 0 ,5 3 9 — 1 ,3 8 2
0 ,3 6 7
0 ,3 7 9
0 ,1 2 9
— 0 ,0 9 5
0 ,2 2 9
1 ,4 6 8
— 1 ,4 8 8 — 0 ,0 7 8 — 2 ,3 6 1 — 0 ,9 9 2
0 ,5 2 9 — 1 ,8 0 5
— 0 ,3 6 1
0 ,1 9 4 — 1 ,0 7 8
-0 ,0 6 3
— 1 ,1 1 0
— 0 ,4 4 0
0 ,1 3 1
-0 ,7 7 2
223.
ЛИТЕРАТУРА1. Б о л ь ш е е Jl. Н. , С м и р н о в Н. В. Таблицы математи
ческой статистики.— М.: Наука, 1965.
2. Б о р о в к о в А. А. Теория вероятностей. М .: Наука, 1976.
3. В о л о д и н Б. Г. , Г а н и н М. П. , Д и н е р И. Я. , К о м а
р о в J1. Б., С в е ш н и к о в А. А. , С т а р о б и н К. Б. Сбор
ник задач по теории вероятностей, математической статистике
и теории случайных функций /Под общей редакцией А. А . Свеш
никова.— М.: Наука, 1965.
4. Г н е д е н к о Б. В. Курс теории вероятностей (изд. 3-е). — М.:
Наука, 1969.
5. К о л м о г о р о в А . Н. Основные понятия теории вероятнос
тей.— М.: Наука, 1974.
6. К о л м о г о р о в А. Н. , Ф о м и н С. В. Элементы теории
функций и функционального анализа.— М .: Наука, 1968.
7. К р а м е р Г. Математические методы статистики (перев. с
англ., изд. 2 -е).—-М .: Мир, 1975.
8. М е ш а л к и н J1. Д. Сборник задач по теории вероятнос
тей.— М.: М ГУ, 1963.
9. Р и о р д а н Д. Введение в комбинаторный анализ.— М.: ИЛ,
1963.
10. С м и р н о в Н. В. , Д у н и н - Б а р к о в с к и й
И. В. Курс
теории вероятностей и математической статистики для техни
ческих приложений (изд. 3 -е ).— М.: Наука, 1969.
11. Ф е л л е р В. Введение в теорию вероятностей и ее приложе
ния (перев. с англ.). — М.: Мир, 1967, т.т. 1— 2.
12. Ч и с т я к о в В. П. К урс теории вероятностей, — М .: Наука,
1978.
224.
Борис Александрович СевастьяновВладимир Павлович Чистяков
Андрей Михайлович Зубков
СБОРНИ К ЗАДАЧ ПО ТЕОРИИ ВЕРОЯТНОСТЕЙ
М ., 1980 г ., 224 стр. с илл.
Редактор И. М . Овчинникова
Техн. редактор Н. В. Кошелева
Корректоры Л. Н. Бородина, Е. В. Сидоркина
ИВ № 11493
Сдано в набор 0 4 .0 3 .8 0 . Подписано к печати 12 .0 8 .8 0 .
Бумага 8 4 X 1 0 8 1/ St, тип. № 2. Литературная гарнитура. Высокая
печать. Условн. печ. л. 11,76. У ч.-и зд. л. 12,75. Тираж 70 000 экз.
Заказ № 14 27. Цена книги 40 коп.
Издательство «Наука»
Главная редакция физико-математической литературы
117071, Москва, В -71, Ленинский проспект, 15
Ордена Октябрьской Революции
и ордена Трудового Красного Знамени
Первая Образцовая типография имени А. А. Жданова
Союзполиграфпрома при Государственном комитете СССР
по делам издательств, полиграфии к книжной торговли.
Москва, М -54, Валовая, 28
Отпечатано с матриц, в тип. № 2 изд-ва «Н аука».
Москва, Шубинский пер., 10, Зак. 3502
225.
Б.Л.СЕВАСТЬЯНОВВ . П. Ч И С Т Я К О В
А. М. З У Б К О В
СБОРНИК ЗАДАЧ
ПО ТЕОРИИ
ВЕРОЯТНОСТЕЙ
щ
о д






























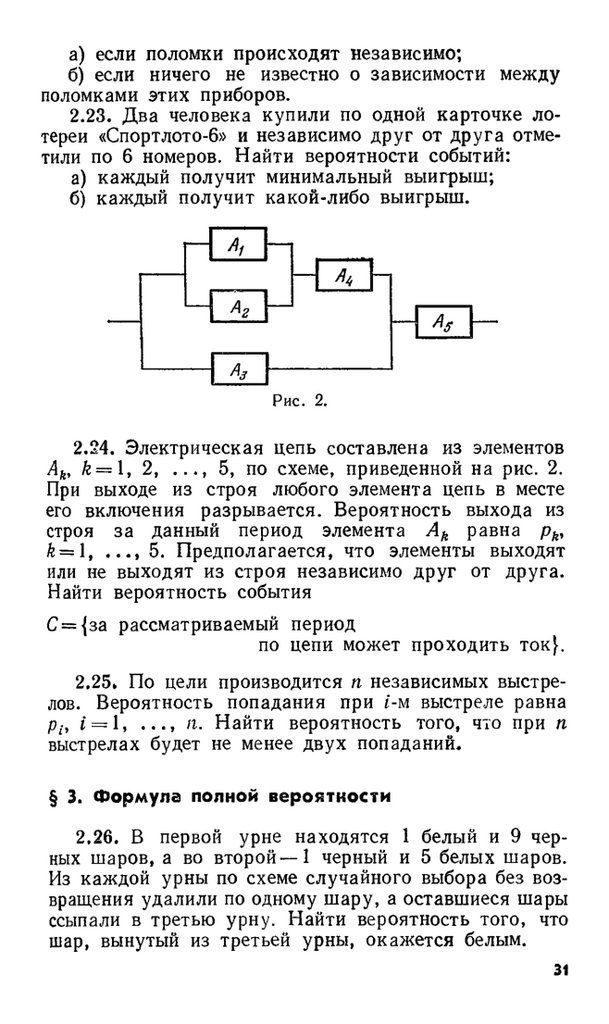
























































































































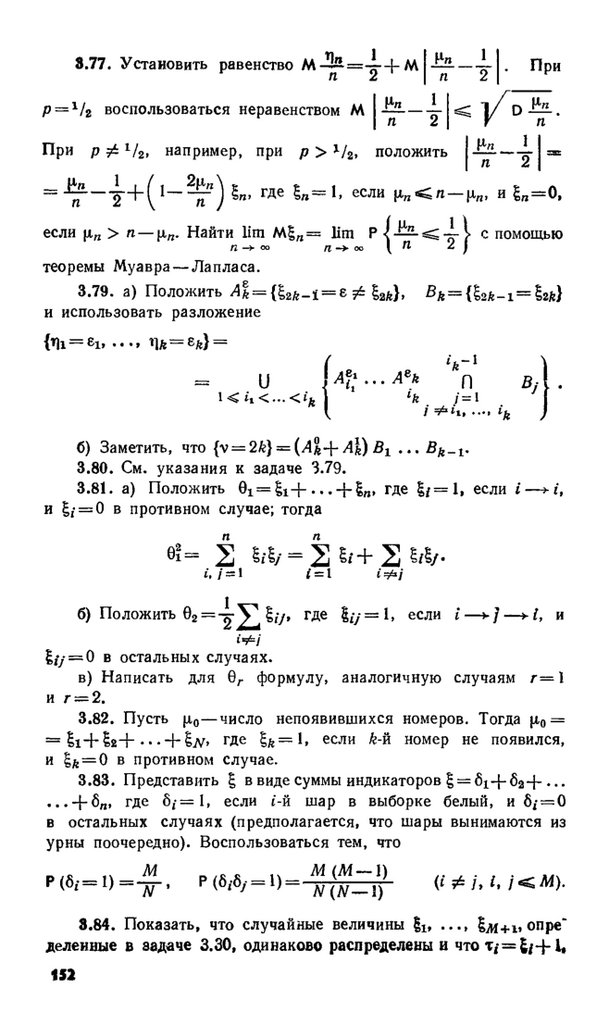















































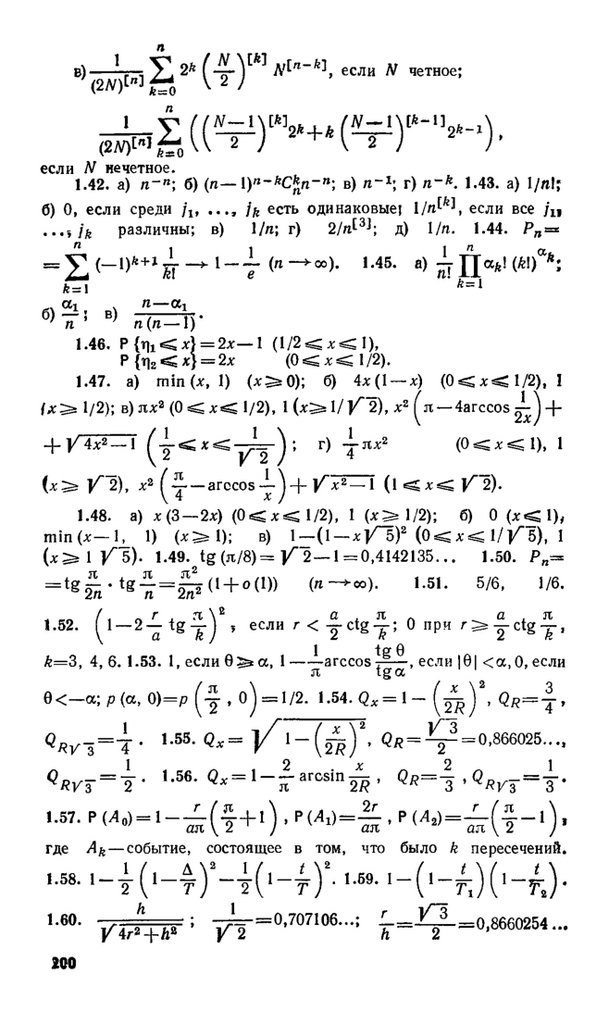

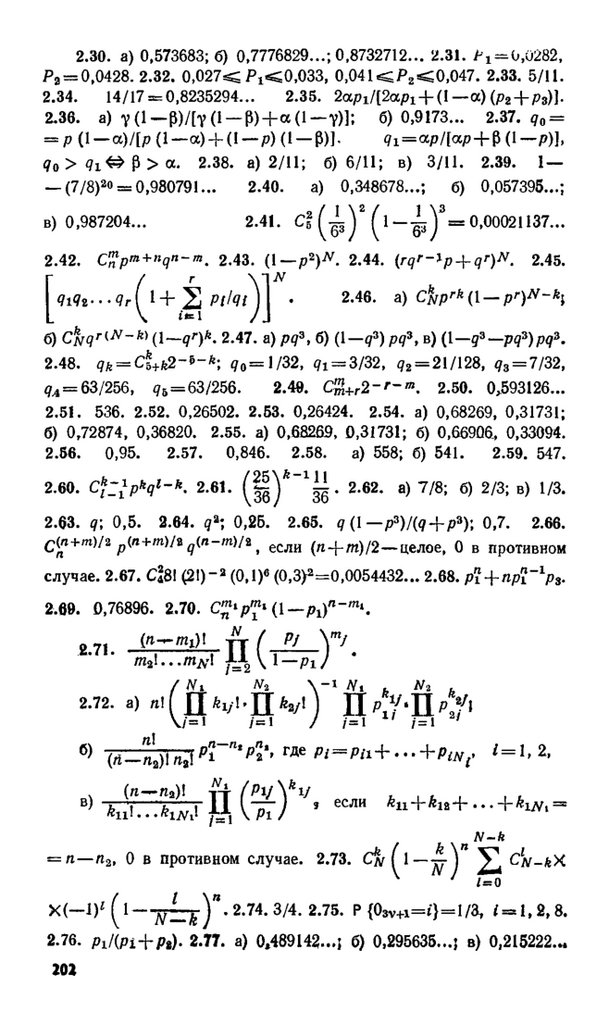






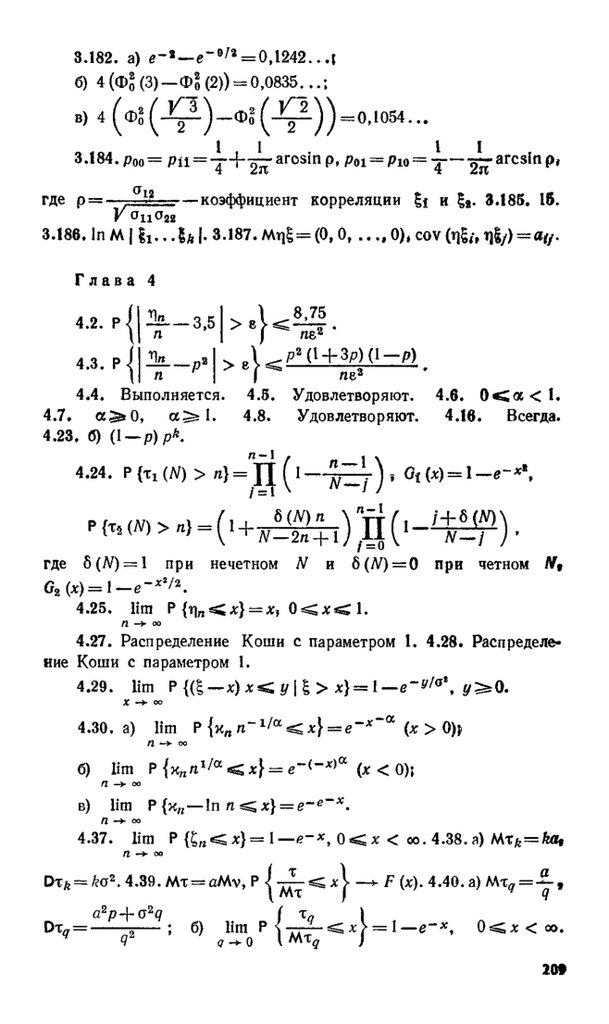





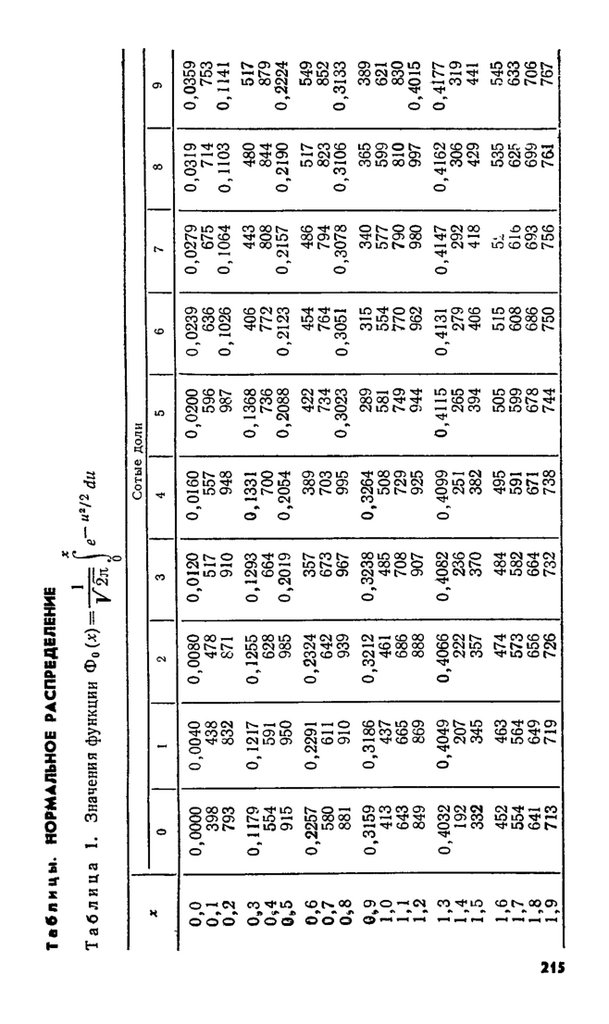
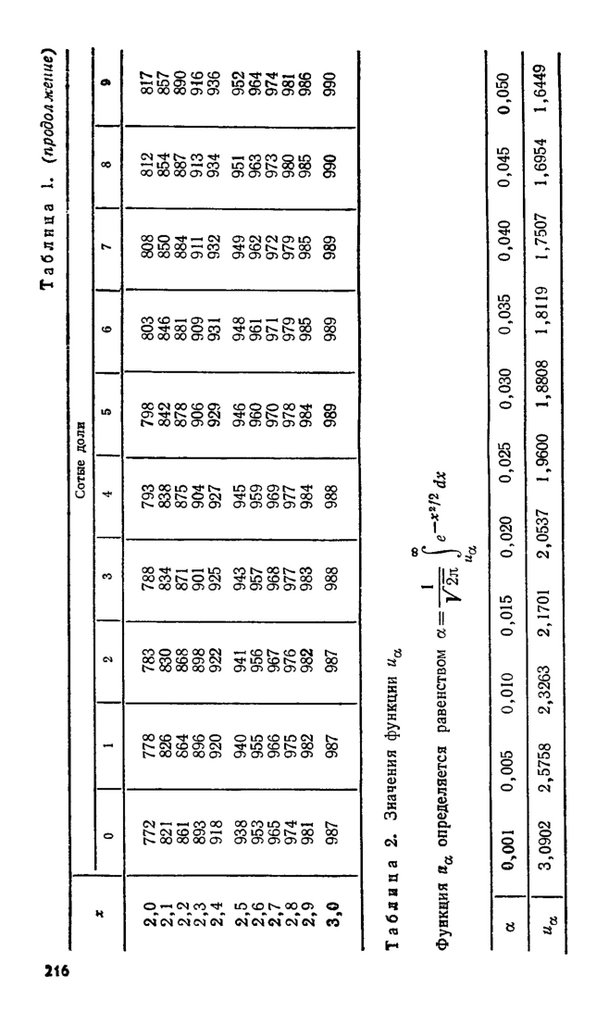
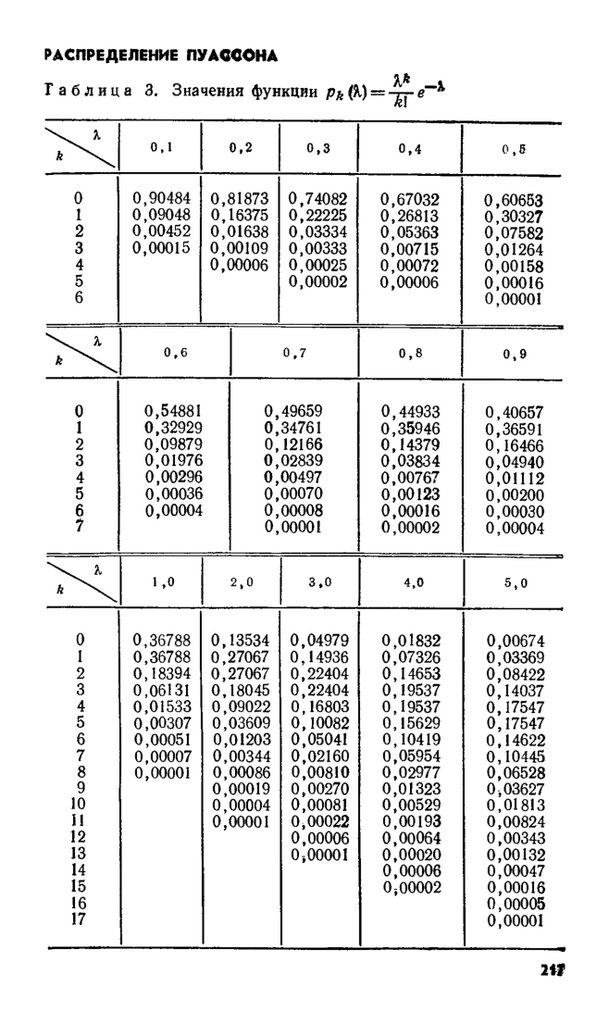








 mathematics
mathematics








