Similar presentations:
Комплексные числа. Практическая работа
1. Практическая работа по теме «КОМПЛЕКСНЫЕ ЧИСЛА»
2.
Алгебраическая форма комплексного числа,его изображение на комплексной плоскости
z2+1=0
z= i-решения уравнения, где
i 1
Определение. Комплексным числом (к.ч.) называют
выражение x+iy, где x,y R, i2= -1.
z=x+iy - алгебраическая форма записи комплексного числа,
x- действительная часть (Rez),
y-мнимая (Imz) часть комплексного числа.
Комплексное число z=yi (при х=0) называется чисто мнимым.
Множество всех комплексных чисел обозначают
C={z:z=x+iy,x,y R},(R C).
3. Пример. Вычислить
-49.Решение.
-49 49 (-1)
49 1 7i.
4. Изображается комплексное число z=x+iy плоскости XOY или радиус - вектором ОМ т.М. Такая плоскость называется комплексной,
Изображаетсякомплексное число
z=x+iy
точкой
M(x,y)
плоскости XOY или радиус - вектором ОМ т.М.
Такая плоскость называется комплексной,
ОХ - действительной, OY – мнимой осями.
Y
M(z)
X
Числа z=x+iy и z=x - iy называются комплексно-сопряженными
Например, z=-3+2i и z=-3-2i.
5. Действия над комплексными числами в алгебраической форме
Пусть z1=x1+iy1, z2=x2+iy2.1) Сложение комплексных чисел:
z1+z2=(x1+х2)+i(y1+y2).
2) Вычитание комплексных чисел: z=z1-z2 z+z2=z1.
z1-z2=( x1-x2)+i(y1-y2).
3) Умножение комплексных чисел:
z1z2=(x1+iy1)(x2+iy2)=( x1x2- y1y2)+i(x1y2+ x2 y1).
4) Деление комплексных чисел:
z1 z1z2
.
z2 z2 z2
6.
Пример. z1=2-7i, z2=-6+4i.Найти z1+ z2; z1-z2; z1·z2; z1/z2.
Решение. z1+z2= (2-7i)+(-6+4i)= 2+(-6)+i(-7+4)=-43i.
z1-z2= (2-7i)-(-6+4i)= 2-(-6)+i(-7-4)= 8-11i.
2= 16+50i.
-12+8i+42i-28i
z1·z2= (2-7i)(-6+4i)=
7. z1=2-7i, z2=-6+4i.
Найтиz1
.
z2
z1 z1z2 (2-7i)(-6 4i) -12 42i-8i 28i2 -12 34i -28
z2 z2 z2 (-6 4i)(-6-4i)
36 16
36-16i2
-40 34i 40 34 i 10 17 i.
52 52
13 26
52
8. Пример. z1=2-7i, z2=-6+4i.
z1Найти
.
z2
Решение.
z1 z1z2
z2 z2 z2
(2-7i)(-6 4i) 40 34 i 10 17 i.
13 26
52 52
(-6 4i)(-6-4i)
z1
10 17
i.
z2
13 26
9.
74i
Пример. Записать в алгебраической форме
.
1 3i
7 4i
7 4i 1 3i
1 3i
1 3i 1 3i
2
7 21i 4i 1 2 i
1 9
5 25i
1 5
i.
10
2 2
10. z 2 3i 7 19 i. 4-5i 41 41
Пример. Записать в алгебраической форме(выполнить действия)
2 3i 7 19
z
i.
4-5i 41 41
Решение. Применим правила умножения, деления и
сложения комплексных чисел в алгебраической форме:
11. z 2 3i 7 19 i 2 3i4 5i 7 19 i
2 3i 7 192 3i 4 5i 7 19
z
i
i
4 5i 4 5i 41 41
4-5i 41 41
2 3i 4 5i 7 19
i
2
16 25i
41
41
8 10i 12i 15i
7 19
i
16 25
41 41
2
12. 8-15 i(10 12 ) 7 19 i 41 41 41
8-15 i(10 12 ) 7 19i
41
41 41
7
41
22
41
i
7
41
19
41
i
41
41
i i.
13. Тригонометрическая и показательная форма комплексного числа
Изобразим комплексное число z=x+iy радиус-вектором OM накомплексной плоскости.
|OM|=r=|z| - модуль комплексного числа,
- угол между осью OX и радиус-вектором ОМ, отсчитываемый
в положительном направлении,
= Argz - аргумент комплексного числа.
Главным значением Argz назовем argz, удовлетворяющее
Y
неравенствам 0 argz 2 или - argz .
М(z)
Тогда Argz=argz+2k , k Z.
X
14. Тригонометрическая форма комплексного числа
z=r(cos +isin )y
r = x y , tg
x
2
2
15.
Пример. z=-2-2i записать в тригонометрической формеr = (-2)2 ( 2)2 = 2 2,
y
5
tg 1 ;
x
4
z=r(cos +isin )
z 2 2(cos
5
4
isin
5
4
).
16.
Формула Эйлераei =cos +isin
17. Показательная форма комплексного числа
z=rei18. z 3 i
Пример. Записать в показательной формеz 3 i
Решение.
Найдем модуль комплексного числа z:
r=
2
2
х у
(
2
2
3) 1 2.
19. z 3 i .
Пример. Записать в показательной формеРешение.
Найдем модуль комплексного числа z:
r = х 2 у 2 ( 3)2 12 2.
Вычислим аргумент М1 I четверти.
3
y
1
, ;
tg
x
3
6
3
i
6
z re 2e
i
z 3 i .
20.
Умножение и деление комплексных чисел втригонометрической форме
Пусть z1=r1(cos 1+isin 1), z2=r2(cos 2+isin 2).
1) Умножение комплексных чисел:
z1z2= r1r2(cos( 1+ 2)+isin( 1+ 2))
2) Деление
комплексных чисел:
z1 r1
cos 1 2 isin 1 2
z2 r2
21. Пусть z1=r1 ei1 , z2=r2 ei 2
Умножение и деление комплексных числе впоказательной форме
Пусть z1=r1 ei 1 , z2=r2 ei 2
1) Умножение
комплексных чисел:
z1 z2 r1 e
i 1
2) Деление
r2 e
i 2
r1 r2 e
комплексных чисел:
i
i 1 2
z1 r1e 1 r1 i( 1 2 )
e
.
i
z2 r2e 2 r2
22. 1 i 3 i.
Пример. Используя тригонометрическую форму комплексногочисла, выполнить указанные действия 1 i 3 i .
Решение.
z1 1 i;
М1(1;–1) IV четверти.
r = 12 ( 1)2 = 2,
y
tg 1,
x
7
.
4
7
7
z1 = 2 cos
i sin
4
4
23. z2 3 i
z2 3 i2
r=
3
2
1 = 2,
3
y
,
tg
x
3
.
6
z 2 = 2 cos i sin
6
6
24. z = 2cos 7 i sin 7
77
z1 = 2 cos
i sin
4
4
z 2 = 2 cos i sin
6
6
z1z2= r1r2(cos( 1+ 2)+isin( 1+ 2))
7
7
z1 z 2 = 2 2 cos
i sin
6 4
6 4
25.
z1z2= r1r2(cos( 1+ 2)+isin( 1+ 2))7
7
z1 z 2 = 2 2 cos i sin
6 4
6 4
23
23
2 2 cos
i sin
.
12
12





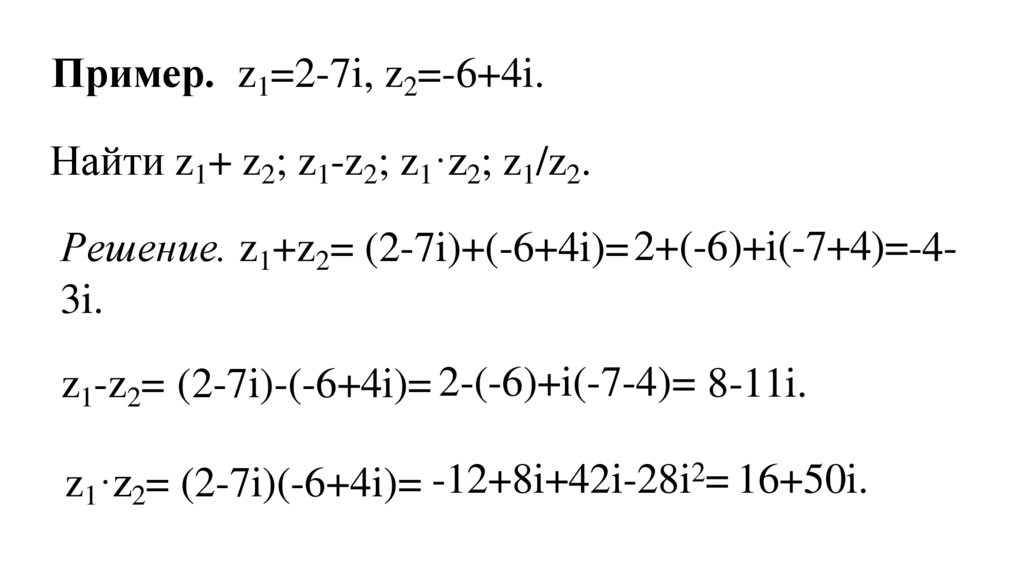
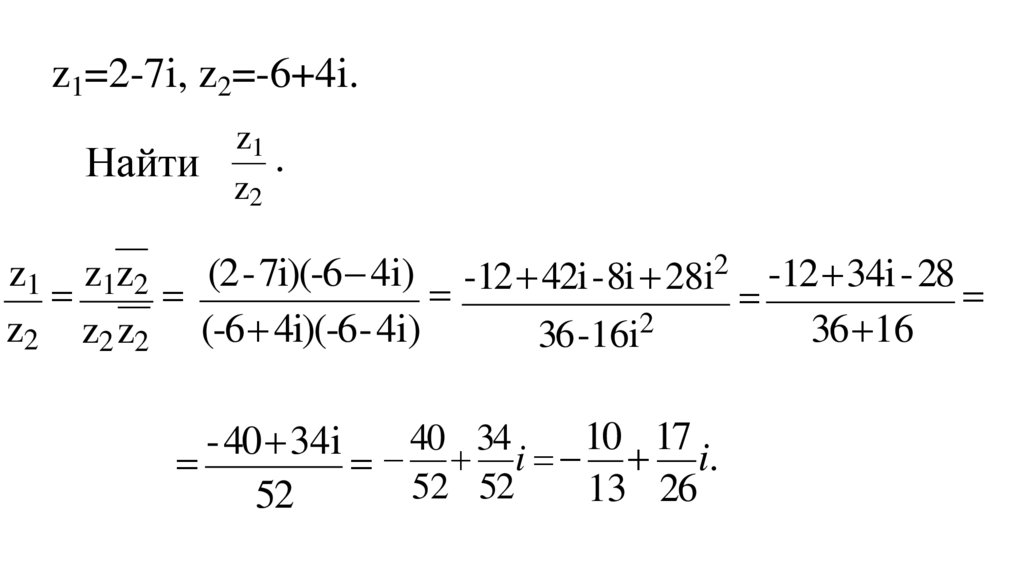



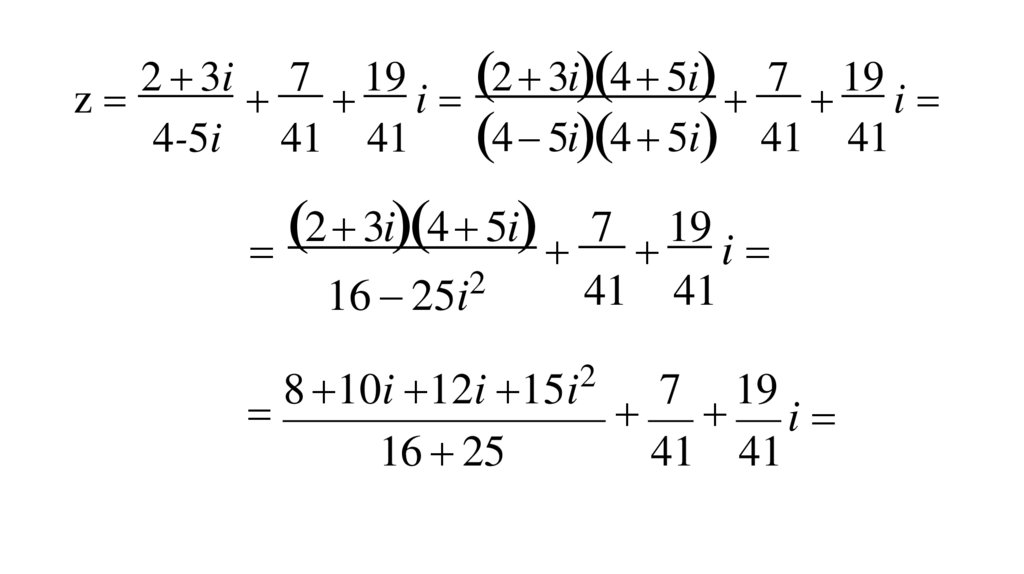
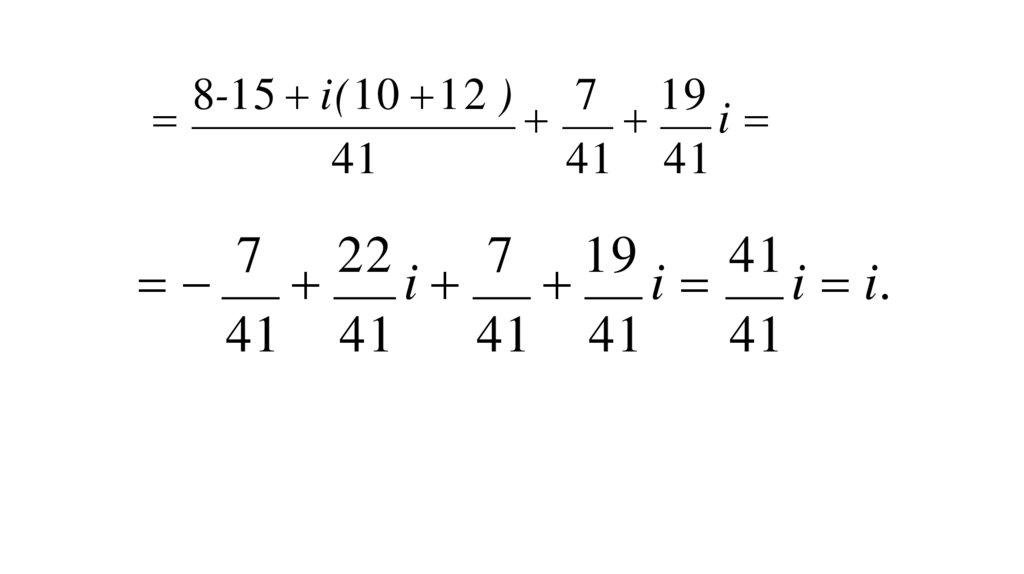










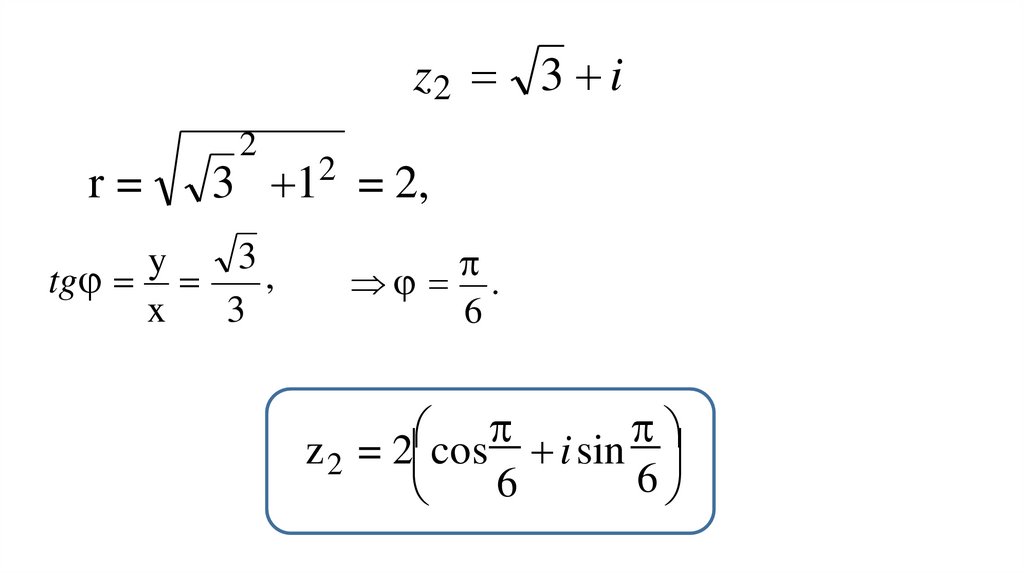
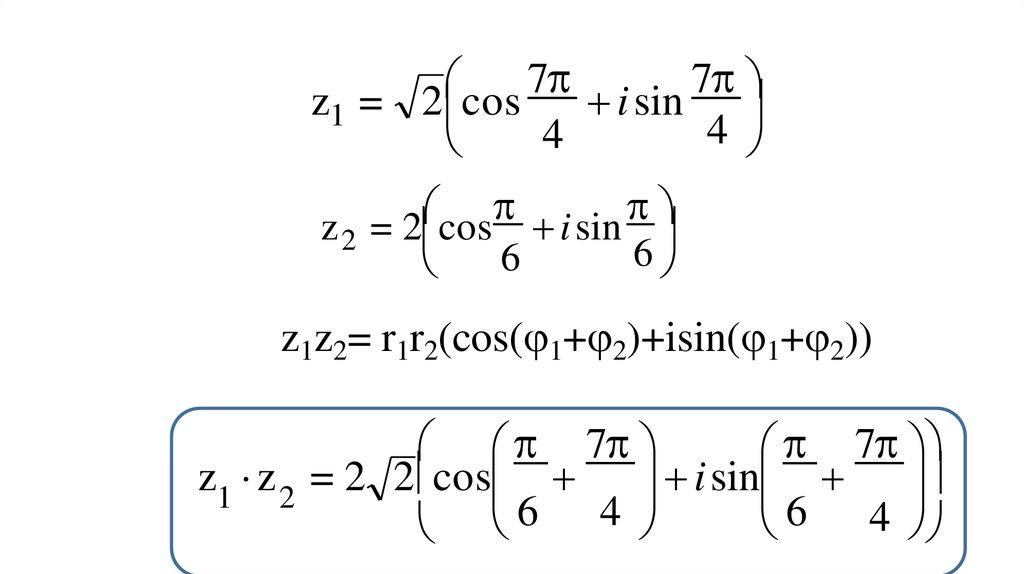

 mathematics
mathematics








