Статистический анализ данных

1. Статистический анализ данных

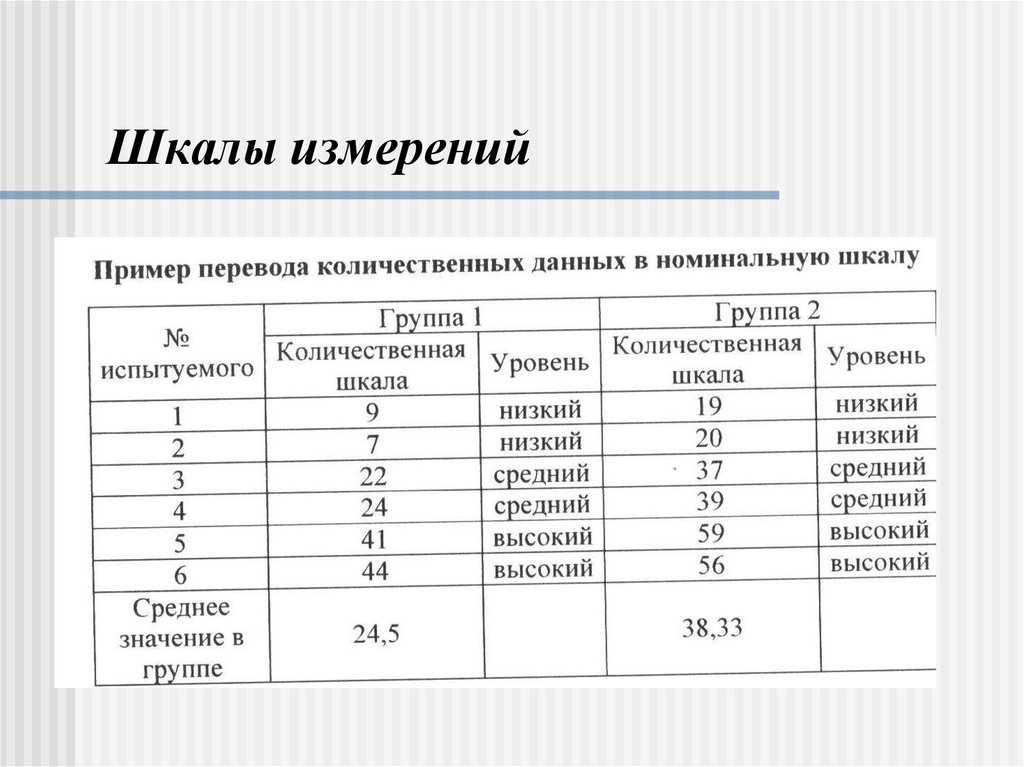
2. Шкалы измерений

Под измерением понимается процесс
приписывания чисел явлениям, при котором в
отношениях чисел отображались отношения
между измеряемыми явлениями

3. Шкалы измерений

Все шкалы делятся на 2 вида:
Неметрические (качественные)
Метрические (количественные)

4. Шкалы измерений

Группу качественных шкал составляют
номинальная и порядковая (ранговая) шкала
К количественным относится шкала
интервалов и шкала отношений

5. Шкалы измерений

Номинальная шкала (шкала категорий)
используются лишь для качественной
классификации. Примерами величин,
измеряемых в этой шкале, служат пол,
национальность, цвет, город и т.д.
Значения этих переменных невозможно
сравнивать по принципу ‘больше-меньше’,
’лучше-хуже’ (Москва лучше Парижа?), а
можно лишь выяснить ‘сколько кого-чего’

6. Шкалы измерений

При использовании номинальной шкалы в
соответствии с некоторым признаком явления
распределяются по классам
Классы могут иметь названия или
обозначаться числами. Значения чисел роли
не играют
Используемые на данной шкале операции
=, , ,

7. Шкалы измерений

Порядковая шкала позволяют ранжировать
(упорядочить) объекты, указав какие из них в
большей или меньшей степени обладают
качеством, выраженным данной переменной.
Однако они не позволяют сказать "насколько
больше" или "насколько меньше".

8. Шкалы измерений

Порядковая шкала позволяют ранжировать
(упорядочить) объекты, указав какие из них в
большей или меньшей степени обладают
качеством, выраженным данной переменной.
Однако они не позволяют сказать "насколько
больше" или "насколько меньше".

9. Шкалы измерений

Порядок нумеруется натуральным числом,
однако разность между числами не
соответствует разности в степени
выраженности свойства между объектами или
явлениями
Допускается использование операций
=, , , , ,

10. Шкалы измерений

Шкала интервалов. В соответствии со
степенью выраженности у объектов
исследуемого признака им приписываются
числа.
Причем разность между числами равна
разности в степени выраженности у объектов
исследуемого свойства.
Например – температурная шкала
Допустимые операции - =, , , , , , +, -.

11. Шкалы измерений

Шкала отношений. В соответствии со
степенью выраженности у объектов
исследуемого признака им приписываются
числа.
Причем отношение между числами,
приписанными двум объектам равно
отношению в степени выраженности у
объектов исследуемого свойства.

12. Шкалы измерений

Шкала отношений. В соответствии со
степенью выраженности у объектов
исследуемого признака им приписываются
числа.
В данной шкале имеет место абсолютный
ноль, означающий отсутствие у объекта
исследуемого признака
Допустимые операции - =, , , , , , +, -,
*, /.

13. Шкалы измерений

Шкала отношений и шкала интервалов
являются метрическими, количественными
шкалами, допускающими возможность их
использования в большинстве методов
статистического анализа

14. Шкалы измерений

15. Описательные статистики

Первый этап обработки данных заключается в
их представлении (описании):
Для показателей измеренных в качественных
шкалах проводится их процентный анализ
Для количественных данных производится
расчет описательных статистик

16. Описательные статистики Различные виды средних значений:

Различные виды средних значений:
Выборочное среднее:
n
1
x xi.
n i 1

17. Описательные статистики Различные виды средних значений:

Среднее геометрическое:
x n x1 x2
xn

18. Описательные статистики Различные виды средних значений:

Среднее гармоническое:
x
n
n
1
x
i 1 i

19. Описательные статистики Структурные средние:

Мода – варианта (значение показателя),
которое встречается в выборке наибольшее
количество раз
Медиана – варианта, находящаяся в
середине вариационного ряда

20. Описательные статистики Различные меры изменчивости

Вариационный размах:
R xmax xmin
Стандартное отклонение
s
n
1
2
( xi x)
n i 1

21. Описательные статистики Различные меры изменчивости

Коэффициент вариации
s
100%
x

22. Описательные статистики Процентили

Процентили – это значение показателя,
меньше которого находится данный процент
наблюдений
Чаще всего используются нижний и верхний
квартили.

23. Описательные статистики Процентили

Нижний квартиль – значение показателя,
меньше которого в вариационном ряду
находится 25% всех наблюдений
Верхний квартиль – значение показателя,
больше которого в вариационном ряду
находится 25% всех наблюдений
Медиана делит вариационный ряд пополам
– это 50 процентиль

24. Описательные статистики оценки ассиметрии и эксцесса

Выборочная ассиметрия
1 n
SK ( xi x)3
n i 1
Выборочный эксцесс
1 n
EX ( xi x) 4 3
n i 1

25. Описательные статистики

Чаще всего при описании данных
информацию представляют в виде среднего
значения и стандартного отклонения или
ошибки среднего.
Однако, это возможно лишь для показателей
имеющих нормальный закон распределения

26. Описательные статистики

Если закон распределения показателей
значимо отличается от нормального закона
распределения, то в расчет описательных
статистик необходимо дополнительно
включить медиану, а также нижний и
верхний квартили