Преобразование логических выражений. ЕГЭ по информатике (задание 15)

1. ЕГЭ по информатике

Задание 15
Преобразование
логических выражений
ЕГЭ по информатике
Автор:
Никитенко Евгений Игоревич
учитель информатики
МБОУ СОШ №10 п.Гирей

2. Выберите номер задания

Задание 1
Задание 2
Задание 3
Задание 4
Задание 5
Задание 6
Задание 7
Задание 8
Задание 9
Задание 10

3. Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наибольшего

Задание 1
Обозначим через ДЕЛ(n, m) утверждение «натуральное число
n делится без остатка на натуральное число m».
Для какого наибольшего натурального числа А формула
тождественно истинна (то есть принимает значение 1 при
любом натуральном значении переменной х)?
¬ДЕЛ(x, А) → (ДЕЛ(x, 6) → ¬ДЕЛ(x, 9))
16
18
17
19

4.

Задание 2
Для какого наименьшего целого неотрицательного числа А
выражение тождественно истинно, т.е. принимает значение 1
при любых целых неотрицательных x и y?
(x + 2y < A) \/ (y > x) \/ (x > 20)
60
62
61
63

5.

Задание 3
Обозначим через m&n поразрядную конъюнкцию
неотрицательных целых чисел m и n.
Так, например, 14&5 = 11102&01012 = 01002 = 4.
Для какого наименьшего неотрицательного целого числа А
формула тождественно истинна (т.е. принимает значение 1
при любом неотрицательном целом значении переменной х)?
x&51 = 0 \/ (x&41 = 0 → x&А ≠ 0)
14
18
16
20

6.

Задание 4
На числовой прямой даны два отрезка:
P = [37; 60] и Q = [40; 77].
Укажите наименьшую возможную длину такого отрезка A, что
формула истинна при любом значении переменной х, т.е.
принимает значение 1 при любом значении переменной х.
(x P) → (((x Q) /\ ¬(x A)) → ¬(x P))
15
19
16
20

7.

Задание 5
Для какого наименьшего целого неотрицательного числа А
выражение тождественно истинно, т.е. принимает значение 1
при любых целых неотрицательных x и y?
(x + 2y < A) \/ (y > x) \/ (x > 30)
91
99
95
103

8.

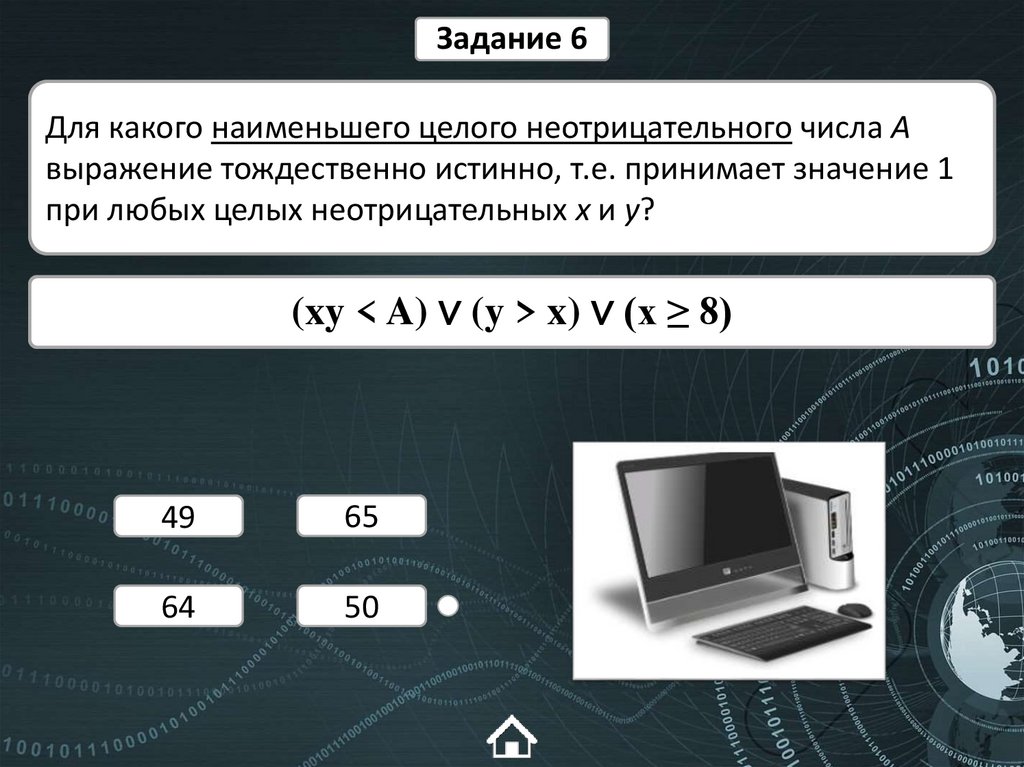
Задание 6
Для какого наименьшего целого неотрицательного числа А
выражение тождественно истинно, т.е. принимает значение 1
при любых целых неотрицательных x и y?
(xy < A) ∨ (y > x) ∨ (x ≥ 8)
49
65
64
50

9.

Задание 7
Для какого наибольшего целого числа А формула
тождественно истинна, то есть принимает значение 1 при
любых целых неотрицательных x и y?
((x ≤ 9) →(x⋅x ≤ A)) ⋀ ((y⋅y ≤ A) → (y ≤ 9))
91
100
81
99

10.

Задание 8
Для какого наибольшего целого неотрицательного числа А
выражение тождественно истинна, то есть принимает
значение 1 при любых целых неотрицательных x и y?
(99 ≠ y + 2x) \/ (A < x) \/ (A < y)
16
64
32
128

11.

Задание 9
Обозначим через m&n поразрядную конъюнкцию
неотрицательных целых чисел m и n.
Так, например, 14&5 = 11102&01012 = 01002 = 4.
Для какого наименьшего неотрицательного целого числа А
формула тождественно истинна (т.е. принимает значение 1
при любом неотрицательном целом значении переменной х)?
x&25 ≠ 0 → (x&17 = 0 → x&А ≠ 0)
8
12
10
14

12.

Задание 10
Для какого наибольшего целого неотрицательного числа А
выражение тождественно истинно, т.е. принимает значение 1
при любых целых неотрицательных x и y?
(48 ≠ y + 2x) \/ (A < x) \/ (A < y)
15
17
16
18

13. 1. ФИПИ: Открытый банк заданий ЕГЭ по информатике 2. Демонстрационные версии ЕГЭ по информатике 2016-2021 года 3. Открытые

Источники:
1. ФИПИ: Открытый банк заданий ЕГЭ по информатике
2. Демонстрационные версии ЕГЭ по информатике 2016-2021 года
3. Открытые варианты ЕГЭ досрочного периода 2020 года
Изображения:
Фон 1 слайда Кнопка «Домой» Кнопка «Выход»
Изображение на 3 слайде Изображение на 4 слайде Изображение на 5 слайде
Изображение на 6 слайде Изображение на 7 слайде Изображение на 8 слайде
Изображение на 9 слайде Изображение на 10 слайде Изображение на 11 слайде
Изображение на 12 слайде