Similar presentations:
Методика решения задания 18 ЕГЭ-2017 по информатике
1. Методика решения задания 18 ЕГЭ-2017 по информатике
учитель информатикиГБОУ «Школа №2107»
Зуева Ю.В.
zueva@2107school.ru
2. Что необходимо знать:
Логические операции:инверсия (логическое отрицание),
конъюнкция (логическое умножение),
пересечение -
дизъюнкция (логическое сложение),
объединение -
Дополнительные операции:
импликация (логическое следование)
Свойство импликации: А В= А В
эквивалентность (логическое равенство)
3. Что необходимо знать:
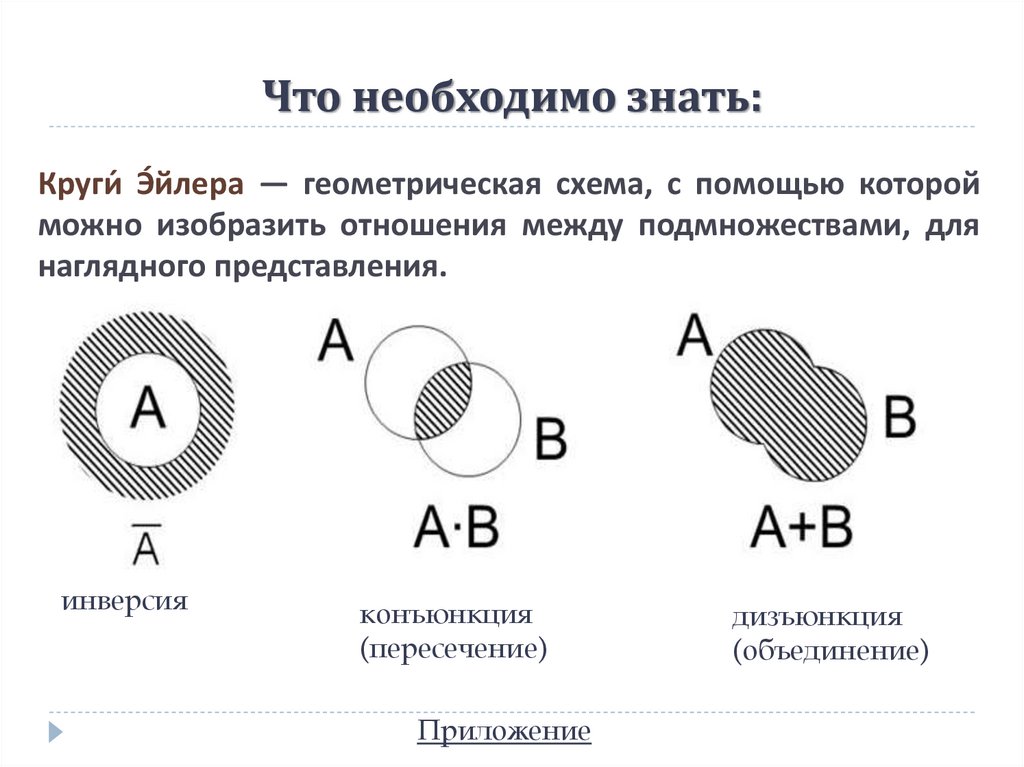
Круги́ Э́йлера — геометрическая схема, с помощью которойможно изобразить отношения между подмножествами, для
наглядного представления.
инверсия
конъюнкция
(пересечение)
Приложение
дизъюнкция
(объединение)
4. Разбор заданий 18
ЭлементамиИзвестно,
множества
А
являются
что
натуральные числа.
выражение
(x {2, 4, 6, 8, 10, 12}) → (((x {4, 8, 12, 116}) ¬(x A)) → ¬(x {2, 4, 6, 8, 10, 12}))
истинно (т. е. принимает значение 1) при любом значении
переменной х. Определите наименьшее возможное значение суммы
элементов множества A.
Обозначим P = {2, 4, 6, 8, 10, 12}, Q = {4, 8, 12, 116}
Запишем логическое выражение:
(x P) (((x Q) (x A)) (x P)) = 1
Преобразуем
импликации:
выражение,
используя
A B = A B
свойство
5.
Преобразуемимпликации:
выражение,
используя
свойство
(x P) ((x Q) (x A)) (x P) =1
Упрощаем по законам де Моргана и ассоциативности:
(x P) (x Q) (x A) (x P) =1
Преобразуем по закону идемпотентности (правило
равносильности):
(x Q) (x P) (x A) =1
6.
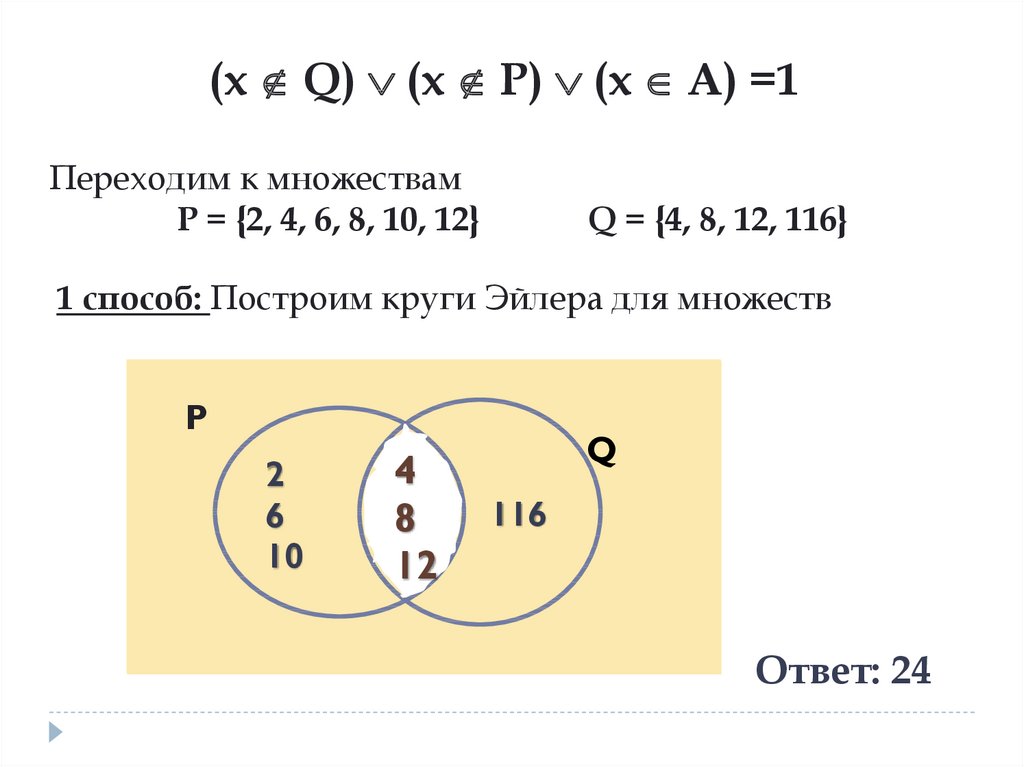
(x Q) (x P) (x A) =1Переходим к множествам
P = {2, 4, 6, 8, 10, 12}
Q = {4, 8, 12, 116}
1 способ: Построим круги Эйлера для множеств
P
2
6
10
4
8
12
Q
116
Ответ: 24
7.
2 способ:(x Q) (x A) (x P) =1
Если (x Q)=1 или (x P)=1, то (x A) – любые значения
Если (x Q)=0 и (x P)=0, то (x A)=1
Переходим к множествам
P = {2, 4, 6, 8, 10, 12}
Q = {4, 8, 12, 116}
Рассмотрим какие элементы множества
одновременно в P и Q
P = {2, 4, 6, 8, 10, 12}
Q = {4, 8, 12, 116}
Именно эти числа должны быть
множеством Аmin={4, 8, 12}
входят
минимальным
Ответ: 24
8.
Введём выражение M & K, обозначающее поразряднуюконъюнкцию M и K (логическое «И» между соответствующими
битами
двоичной
записи).
Определите
наибольшее
натуральное число A, такое что выражение
(X & A 0 ) ((X & 20 = 0) (X & 5 0))
тождественно истинно (то есть принимает значение 1 при
любом натуральном значении переменной X)?
Упростим логическое выражение:
(X & A 0 ) ( (X & 20 = 0) (X & 5 0)) = 1
(X & A = 0 ) (X & 20 0) (X & 5 0) = 1
9.
(X & A = 0 ) (X & 20 0) (X & 5 0) = 1Рассмотрим случай:
(X & A = 0 ) = 1
(X & 20 0) = 0
(X & 5 0) = 0
Y1 Y2
0
0
0
1
1
0
1
1
Преобразуем логические выражения:
X&A=0
X & 20 = 0
X&5=0
Для данных уравнений составим маску Х
Y1 Y2
0
1
1
1
10.
X & 20 = 0Представим числа в двоичной системе счисления:
2010 = 16 + 4 = 101002
X10 = ?????2
Выполним поразрядную конъюнкцию:
2010 = 101002
Х10 = ?????2
000002
Составим маску для Х, где * - любое двоичное
число
Х=0*0**
11.
X&5=0Представим числа в двоичной системе счисления:
510 = 4 + 1= 001012
X10 = 0*0**2
Выполним поразрядную конъюнкцию
510 = 001012
Х10 = 0 *0* *2
000002
Составим маску для Х=0*0*0
12.
X&A=0Выполним
поразрядную
конъюнкцию,
представим А10=abcde2,
где a, b, c, d, e – двоичные цифры.
Х10 = 0*0*02
А10 = abcde2
000002
Получим b=0, d=0,
a, c, e – любые двоичные цифры.
A10 = a0c0e2
A max = 101012 = 16 + 4 + 1 =2110
13.
Демоверсия 2017Обозначим через M & N поразрядную конъюнкцию
неотрицательных целых чисел M и N. Так, например, 14 & 5 =
11102 & 01012 = 01002 = 4. Для какого наименьшего
неотрицательного целого числа А формула
(x & 51 = 0) ((x & 41 = 0) → (x & А ≠ 0))
тождественно истинна (т. е. принимает значение 1 при
любом неотрицательном целом значении переменной х)?
Упростим логическое выражение:
(X & 51 = 0 ) ( (X & 41 = 0) (X & А 0)) = 1
(X & 51 = 0 ) ( (X & 41 0) (X & А 0)) = 1
14.
(X & 51 = 0 ) (X & 41 0) (X & А 0) = 1Рассмотрим случай:
Преобразуем:
(X & A 0 ) = 1
X&A 0
(X & 41 0) = 0
X & 41 = 0
(X & 51= 0) = 0
X & 51 0
Рассмотрим поразрядную
выражения: X & 41 = 0
конъюнкцию
для
Представим числа в двоичной системе счисления:
4110 = 32 + 8 + 1= 1010012
X10 = ??????2
15.
X & 41 = 0Выполним поразрядную конъюнкцию:
4110 = 1010012
Х10 = ??????2
0000002
Составим маску для Х, где * - любое двоичное
число
Х=0*0**0
16.
X & 51 0Представим числа в двоичной системе счисления:
5110 = 32 + 16 + 2 + 1= 1100112
X10 = 0*0**02
Выполним поразрядную конъюнкцию
5110 = 1100112
Х10 = 0*0**02
0?00?02
Составим маски для Х:
Х=010**0
Х=0*0*10
Х=010*10
17.
X&A 0Выполним поразрядную конъюнкцию, представим
А10=abcdef2,
где a, b, c, d, e, f – двоичные цифры.
Х10 = 010**02
Х10 = 0*0*102
Х10 = 010*102
А10 = abcdef2
А10 = abcdef2
А10 = abcdef2
0b0??02
0?0?e02
0b0?e02
Заметим, что b=1 и e=1 для всех масок Х
Аmin = 0100102 = 16 + 2 = 1810
18.
Введём выражение M & K, обозначающее поразряднуюконъюнкцию M и K (логическое «И» между соответствующими
битами двоичной записи). Определите наибольшее натуральное
число a, такое что выражение
(((x & a 0) (x & 12 = 0)) ((x & a = 0) (x & 21 0))) ((x & 21 =0) (x & 12=0))
тождественно истинно (то есть принимает значение 1 при
любом натуральном значении переменной X)?
Обозначим A=(x&a=0),
P=(x&12=0),
Q=(x&21=0)
Запишем логическое выражение:
(( A P) (A Q)) (Q P) = 1
Преобразуем по свойству импликации:
( A P) (A Q) (Q P) = 1
Преобразуем по закону де Моргана:
A P (A Q) (Q P) = 1
19.
По закону ассоциативности:(A (A Q) ) ( P (Q P)) = 1
Преобразуем по законам поглощения и
поглощения отрицания:
A ( P Q) = 1
A P Q = 1
(x & a = 0) (x & 12 0) (x & 21 = 0) = 1
20.
(X & 21 = 0) (X & 12 0) (X & A = 0) = 1Рассмотрим случай:
Преобразуем:
(X & A = 0 ) = 1
X&A=0
(X & 12 0) = 0
X & 12 = 0
(X & 21 = 0) = 0
X & 21 0
Рассмотрим поразрядную
выражения: X & 12 = 0
конъюнкцию
для
Представим числа в двоичной системе счисления:
1210 = 8 + 4= 011002
X10 = ?????2
21.
X & 12 = 0Выполним поразрядную конъюнкцию:
4810 = 011002
Х10 = ??????2
0000002
Составим маску для Х, где * - любое двоичное
число
Х=*00**
22.
X & 21 0Представим числа в двоичной системе счисления:
2110 = 16 + 4 + 1= 101012
X10 = *00**2
Выполним поразрядную конъюнкцию
2110 = 101012
Х10 = *00**2
?000?2
Составим маски для
Х = 100**
Х = *00*1
Х = 100*1
23.
X&A=0Выполним поразрядную конъюнкцию, представим
А10=abcde2,
где a, b, c, d, e, – двоичные цифры.
Х10 = 100**2
Х10 = *00*12
Х10 = 100*12
А10 = abcde2
А10 = abcde2
А10 = abcde2
000002
000002
00000
2
Заметим, что a = 0, d = 0, e = 0, b и c – любые
значения для любых значений Х
Аmax = 011002 = 8 + 4 = 1210
24.
Введём выражение M & K, обозначающее поразряднуюконъюнкцию M и K (логическое «И» между соответствующими
битами двоичной записи). Определите наименьшее натуральное
число A, такое что выражение
(X & 56 0) ((X & 48 = 0) (X & A 0))
тождественно истинно (то есть принимает значение 1 при
любом натуральном значении переменной X)?
Преобразуем логическое выражение:
(X & 56 0) ((X & 48 = 0) (X & A 0)) = 1
(X & 56 0) ( (X & 48 = 0) (X & A 0)) = 1
(X & 56 = 0) (X & 48 0) (X & A 0) = 1
25.
(X & 56 = 0) (X & 48 0) (X & A 0) = 1Рассмотрим случай:
Преобразуем:
(X & A 0 ) = 1
X&A 0
(X & 48 0) = 0
X & 48 = 0
(X & 56 = 0) = 0
X & 56 0
Рассмотрим поразрядную
выражения: X & 48 = 0
конъюнкцию
для
Представим числа в двоичной системе счисления:
4810 = 32 + 16 = 1100002
X10 = ??????2
26.
X & 48 = 0Выполним поразрядную конъюнкцию:
4810 = 1100002
Х10 = ??????2
0000002
Составим маску для Х, где * - любое двоичное
число
Х=00****
27.
X & 56 0Представим числа в двоичной системе счисления:
5610 = 32 + 16 + 8= 1110002
X10 = 00****2
Выполним поразрядную конъюнкцию
5610 = 1110002
Х10 = 00****2
00?0002
5610 = 1110002
Х10 = 00****2
0010002
Составим маску для Х=001***
28.
X&A 0Выполним
поразрядную
конъюнкцию,
представим А10=abcdef2,
где a, b, c, d, e, f – двоичные цифры.
Х10 = 001***2
А10 = abcdef2
00с??? 2
Заметим, что с=1, a, b – любые значения для
любых значений Х
Аmin = 0010002 = 810
29.
Пусть P – множество всех 8-битовых цепочек, начинающихся с1, Q – множество всех 8-битовых цепочек, оканчивающихся на
000, а A – некоторое множество произвольных 8-битовых
цепочек. Сколько элементов содержит минимальное множество
A, при котором для любой 8-битовой цепочки x истинно
выражение
¬(x A) (¬(x P) (x Q))
Преобразуем
импликации:
логическое
выражение
по
(x A) ¬(x P) (x Q) = 1
(x A) (x P) (x Q) = 1
свойству
30.
Рассмотрим случай:Преобразуем:
(X A) = 1
X A
(X P) = 0
X P
(X Q) = 0
X Q
Рассмотрим множества P и неQ:
P – множество всех 8-битовых цепочек, начинающихся с 1,
Q – множество всех 8-битовых цепочек, оканчивающихся на 000,
1
*
*
*
*
?
?
*- любое двоичное число (0 или 1)
??? – не совпадает с 000
?
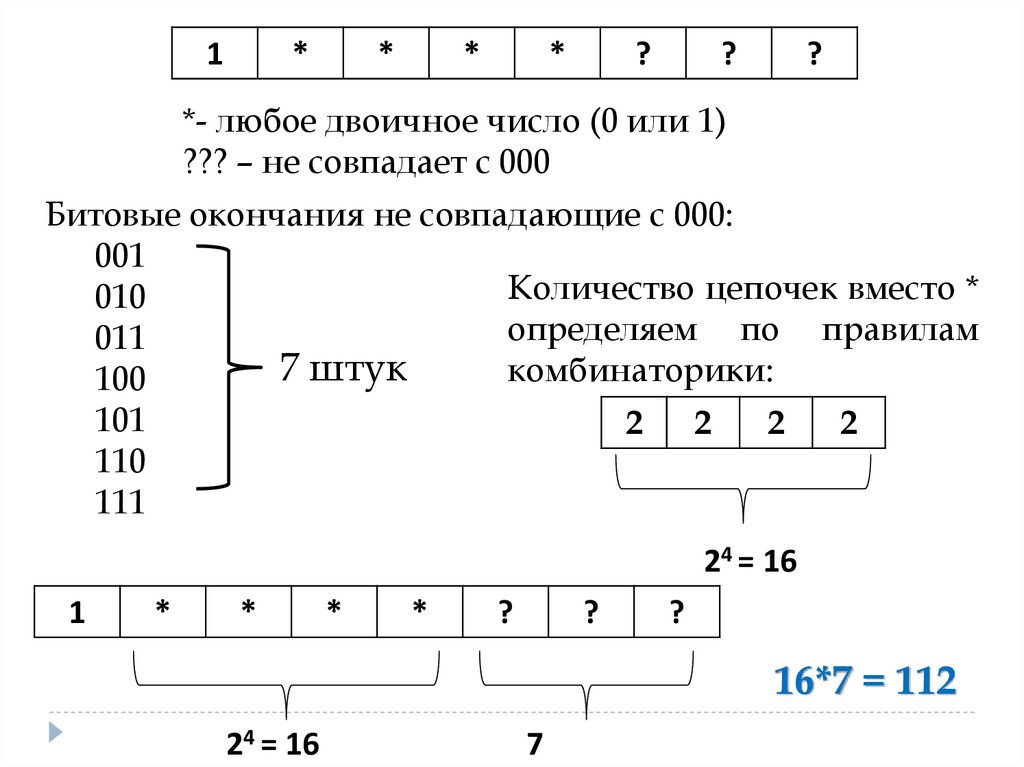
31.
1*
*
*
*
?
?
?
*- любое двоичное число (0 или 1)
??? – не совпадает с 000
Битовые окончания не совпадающие с 000:
001
Количество цепочек вместо *
010
определяем по правилам
011
7 штук
комбинаторики:
100
101
2
2
2
2
110
111
24 = 16
1
*
*
*
*
?
?
?
16*7 = 112
24 = 16
7
32. Список источников
http://kpolyakov.narod.ru/download/B15.doc
http://ege.yandex.ru/informatics
http://ege-go.ru/zadania/grb/b15/
Демовариант ЕГЭ по информатике 2016
http://kpolyakov.narod.ru/download/ege18.doc
тренировочная работа по информатике от 29.11.16





























 informatics
informatics








