Стойкость криптоалгоритмов в условиях атак с использованием квантового компьютера. Лекция 4

1. Лекция 4

Стойкость криптоалгоритмов в условиях атак
с использованием квантового компьютера
1. Принципы квантовых вычислений.
2. Алгоритм ускоренного поиска Гровера.
3. Алгоритм факторизации числа на
квантовом компьютере Питера Шора
1

2. Понятие о квантовых вычислениях

• В классических ЭВМ бит задается ячейками
с двумя устойчивыми состояниями: триггер,
конденсатор, магнитный домен…Одно из
этих состояний условно обозначается 0,
другое 1.
• Для хранения нескольких бит используются
регистры как совокупность ячеек для
хранения бит
1
1
2
0
3
1
n-1
0
n
1
Для хранения 2n чисел
нужно 2n регистров
2

3.

• В квантовом компьютере бит это квантовая система с двумя
возможными физическими состояниями элементарной
частицы: спин электрона в магнитном поле, энергетический
уровень атома водорода, две поляризации фотона.
• Математическая модель состояния частицы описывается
вектором в 2-х мерном пространстве:
(1)
0 0 1 1
где 0 , 1 - состояния системы, а 0 и 1 - комплексные
амплитуды состояния.
Соотношение (1) называетcя квантовым битом или q-битом.
Квадраты модулей являются вероятностями обнаружения
частицы в соответствующих состояниях: 0 , 1
при измерении . 0 2 12 1
Состояние частицы выясняется только после измерения, а текущее
(скрытое) состояние представляет собой линейную смесь (1).
3

4. Обозначения

Состояние кубита x 0 0 1 1
принято
обозначать
Или вектор-столбцом 0 - кет-вектор,
1
Или вектор-строкой 0 1 - бра-вектор
Примеры.
1
0 ,
0
0
1 .
1
4

5. n- кубитовый регистр

1
2
3
n-1
n
▪▫
▫▪
▪▫
▫▪
▪▫
В одном регистре сразу
может быть 2n возможных чисел
С увеличением числа ячеек в регистре состояния частиц оказываются
взаимосвязанными (сцепленными). Например система из 2-х кубитов
может находиться в состоянии
λ00│00>+ λ01│01>+
λ10│10>+ λ11│11>
При обобщении на n-кубитовый регистр по аналогии описывается линейной
комбинацией.:
2n 1
x x
x 0
где
x 00
01
- состояние регистра
5

6.

Вычисление функции в кубитовом
регистре
Пусть задана функция f(x), преобразующая n-разрядное число x в
m-разрядное число f(x). Для описания функции можно построить таблицу
x
f(x)
00000
001
00001
010
…
…
11111
110
2n строк
В квантовом компьютере достаточно лишь один раз выполнить
преобразование f(х) исходного регистра из n ячеек, где содержатся все
n-разрядные числа x и получить все значения функции.
Для ее записи нужно иметь m ячеек памяти Всего нужно иметь n+m кубитых ячеек..
7

7. Вычисление функции в кубитовом регистре

x
2
8

8.

Идея квантовых вычислений
• Принцип квантовых вычислений заключен в увеличении
модуля комплексных амплитуд │λx0│тех состояний x0 , f ( x)
,
которые хотелось бы получить в результате
считывания.
• Процесс вычисления – последовательность унитарных
преобразований ненаблюдаемого состояния регистра.
Унитарное преобразование задается унитарной матрицей - Н. Матрица
Называется унитарной , если H H где
- комплексно сопряженная матрица
Этим обеспечивается обратимость преобразования.
Для обратимых преобразований выполняется условие нормировки
0 2 12 1
9

9. Идея квантовых вычислений

Элементарные преобразования
Нaзвание и Результат
Матрица
обозначение преобразования
0 0
Тождественное
преобразование II
1 1
Отрицание X
0 1
1 0
Фазовый сдвиг -Z
0 0
1 1
Фазовый сдвиг
с отрицанием Y
Преобразование
Адамара Н
CNOT
Прибавление ко
второму биту
первого
mod2
0 0
1 1
1
(0 1)
2
1
1
(0 1)
2
00 00
0
01 01
10 11
11 10
1 0
0 1
0 1
1 0
1 0
0 1
0 1
1 0
1 1 1
2 1 1
1
0
0
0
0
1
0
0
0
0
0
1
0
0
1
0
10

10. Элементарные преобразования

Задачи, решаемые с помощью квантового
компьютера
• Проверка является ли булева функция константой
– алгоритм Дойча-Джоза.
• Задача поиска решения уравнения f ( x) 1 , где
функция принимает значения (0,1) – алгоритм
Гровера.
• Квантовое преобразование Фурье.
• Задача факторизации числа – алгоритм Шора.
• Задача дискретного логарифмирования-алгоритм
Шора
11

11. Задачи, решаемые с помощью квантового компьютера

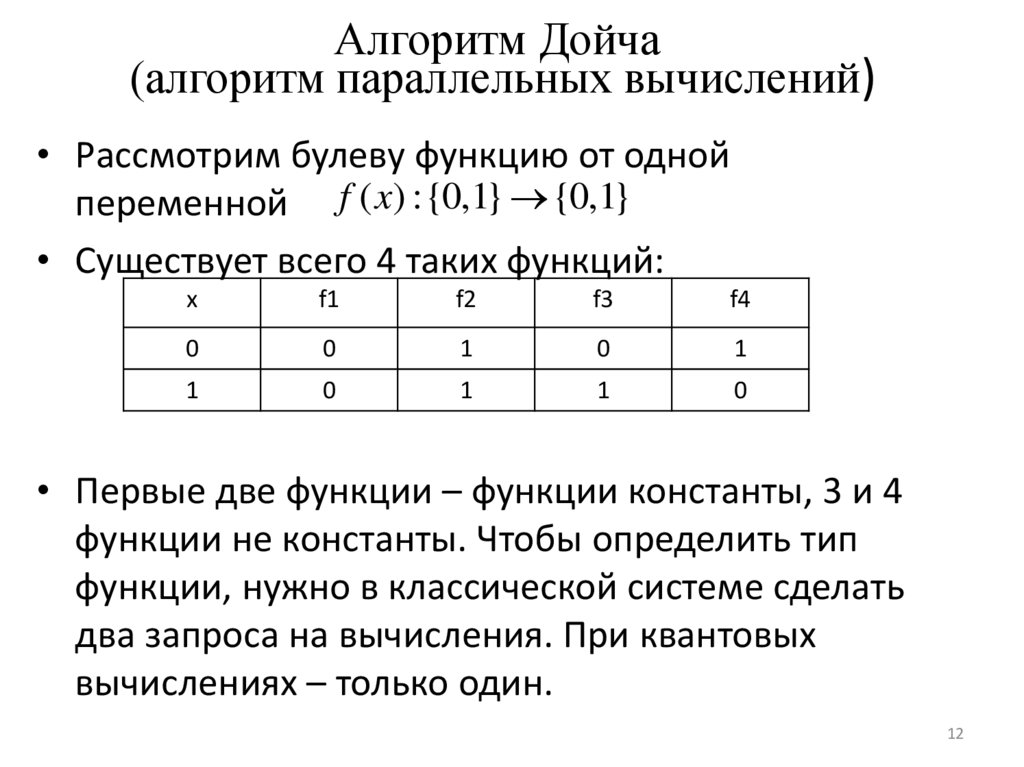
Алгоритм Дойча
(алгоритм параллельных вычислений)
• Рассмотрим булеву функцию от одной
переменной f ( x) :{0,1} {0,1}
• Существует всего 4 таких функций:
x
f1
f2
f3
f4
0
0
1
0
1
1
0
1
1
0
• Первые две функции – функции константы, 3 и 4
функции не константы. Чтобы определить тип
функции, нужно в классической системе сделать
два запроса на вычисления. При квантовых
вычислениях – только один.
12

12. Алгоритм Дойча (алгоритм параллельных вычислений)

Решение
Запишем состояния 0 и1 кубита
q 0 0 1 1
0 1 0 0 1
1 0 0 1 1
1
или 0
0
0
или 1
1
Сначала возьмем систему из одного кубита в
базисном состоянии, соответствующем логическому
нулю.
К полученному кубиту применяем преобразование
Адамара
1 1 1
H1
1
1
2
13

13. Решение

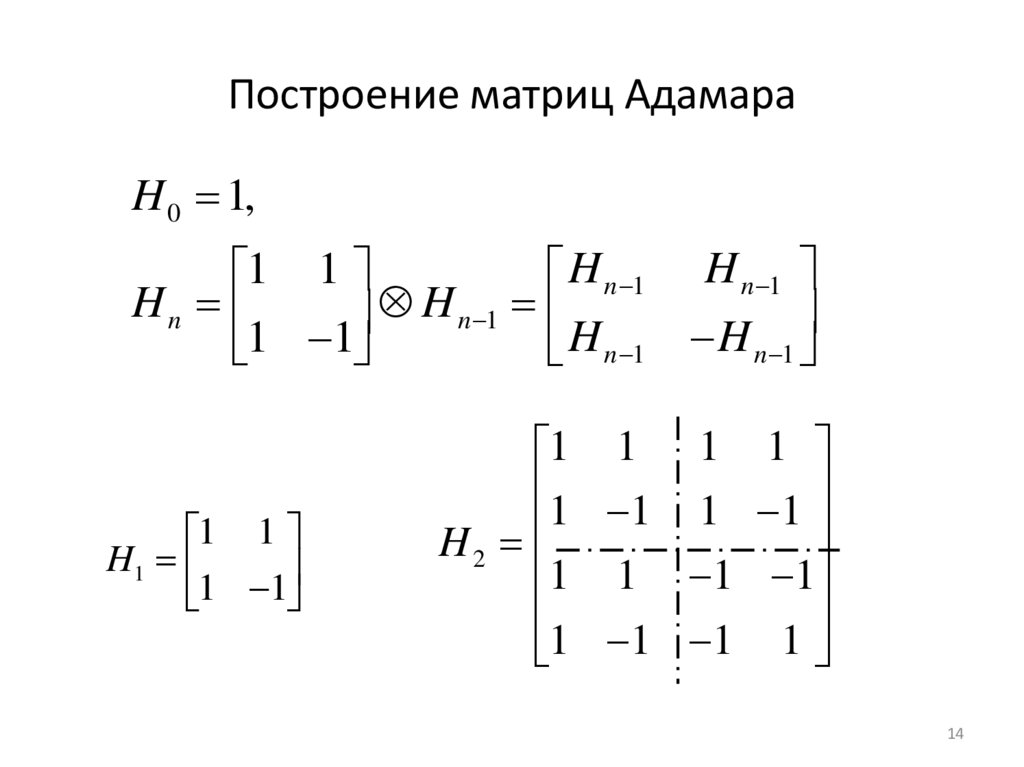
Построение матриц Адамара
H 0 1,
H n 1 H n 1
1 1
Hn
H n 1
H
H
1
1
n 1
n 1
1 1
H1
1
1
1 1 1 1
1 1 1 1
H2
1 1 1 1
1 1 1 1
14

14. Построение матриц Адамара

H 0
1 1 1 1 1 1 1
(0 1)
2 1 1 0
2 1
2
Это λi
• Далее выполняем еще одно преобразование,
которое называется фазовый запрос O f
1 ( 1) f (0)
Of H 0
2 0
0 1 1 ( 1) f (0) 1
f (0)
f (1)
((
1)
0
(
1)
1)
f (1)
f (1)
( 1) 1
2 ( 1)
2
• Далее еще раз применяем преобразование
Адамара.
1 1 1 ( 1) f (0) ( 1) f (0) ( 1) f (1)
( 1) f (0) ( 1) f (1)
HO f H 0
0
1
f (1)
2 1 1 ( 1)
2
2
15

15.

x
f1
f2
f3
f4
0
0
1
0
1
1
0
1
1
0
• Таким образом после этих преобразований мы
получаем суперпозицию состояний с
( 1) ( 1)
( 1) ( 1)
амплитудами
,
f (0)
0
f (1)
2
f (0)
1
f (1)
2
• Для функции типа константы f (0) f (1) получаем
амплитуды 0 1, 1 0 и измерение конечного
2
P
1 определит,
состояния с вероятностью
0
что система находится в состоянии 0 .
16

16.

• Для функции, не являющейся константой
f (0) f (1) амплитуды равны 0 0, 1 1
2
и с вероятностью P 1 1 получим
состояние 1 .
• Таким образом в процесс только одного
измерения мы получаем результат ,
который означает, что функция f ( x) является
константой или не константой в противном
случае.
17

17.

Алгоритм Дойча-Джоза
• Обобщает алгоритм Дойча на случай
функции n переменных f ( x , x , , x ) : 0,1 0,1
• Позволяет определить за одно измерение
является ли функция константой или
сбалансированной функцией , т.е. если в
половине случаев она принимает значение
0, а в другой половине 1.
• Амплитуда 0 принимает значение 1
если функция константа и 0, если она
сбалансирована.
n
0
1
n 1
18

18. Алгоритм Дойча-Джоза

Алгоритм ускоренного поиска (алгоритм
Гровера)
Рассмотрим решение уравнения f ( x ) 1, где
функция f(x) принимает значения{0,1},
но только при одном значении.
f ( xi ) 1, f ( x j ) 0, j i
Состояние системы в общем виде можно записать
так
2n 1
i xi 0 x0 1 x1 n 1 x n 1
2
2
i 0
Где i амплитуда i-го состояния.
19

19. Алгоритм ускоренного поиска (алгоритм Гровера)

• Идея алгоритма Гровера состоит в том,
чтобы увеличить, например, │λx0│ за счет
других │λx│.
• Этого можно добиться k кратным
преобразованием диффузии.
[ψ>=DD…D[ψ1>,
где [ψ1> – начальный вектор состояния,
D – матрица преобразования.
20

20.

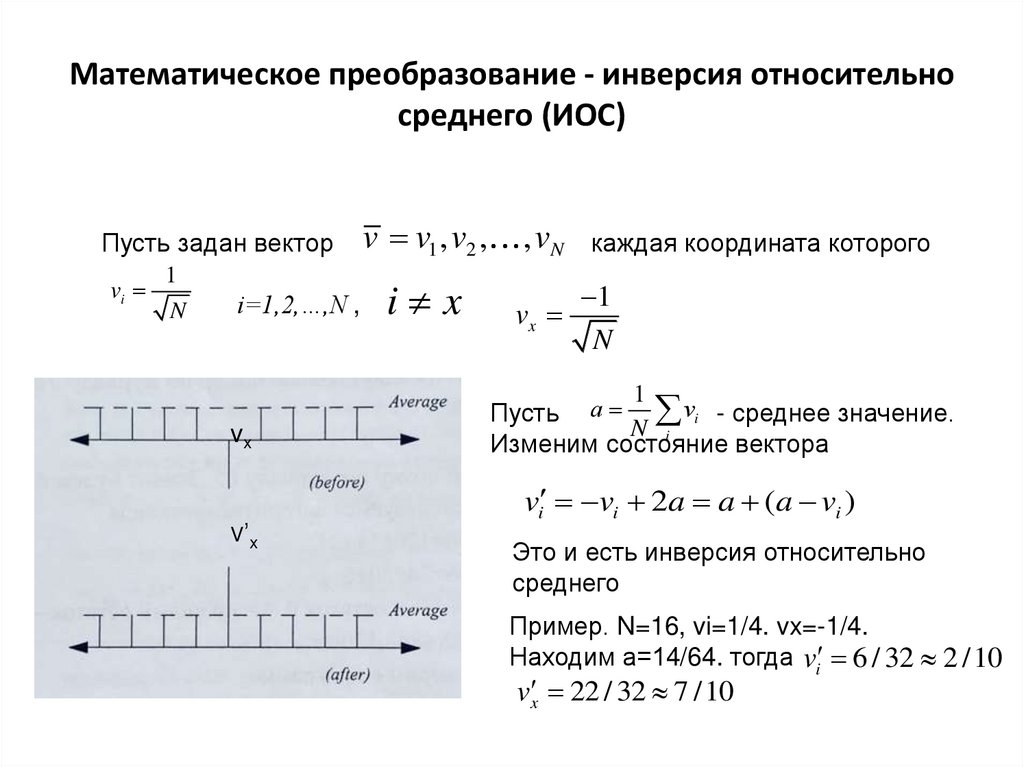
Математическое преобразование - инверсия относительно
среднего (ИОС)
Пусть задан вектор
vi
1
N
i=1,2,…,N ,
vx
V’x
v v1 , v2 ,
i x
, vN
каждая координата которого
1
vx
N
1
а
Пусть
vi - среднее значение.
N i
Изменим состояние вектора
vi vi 2a a (a vi )
Это и есть инверсия относительно
среднего
Пример. N=16, vi=1/4. vx=-1/4.
Находим а=14/64. тогда vi 6 / 32 2 /10
v x 22 / 32 7 /10

21. Математическое преобразование - инверсия относительно среднего (ИОС)

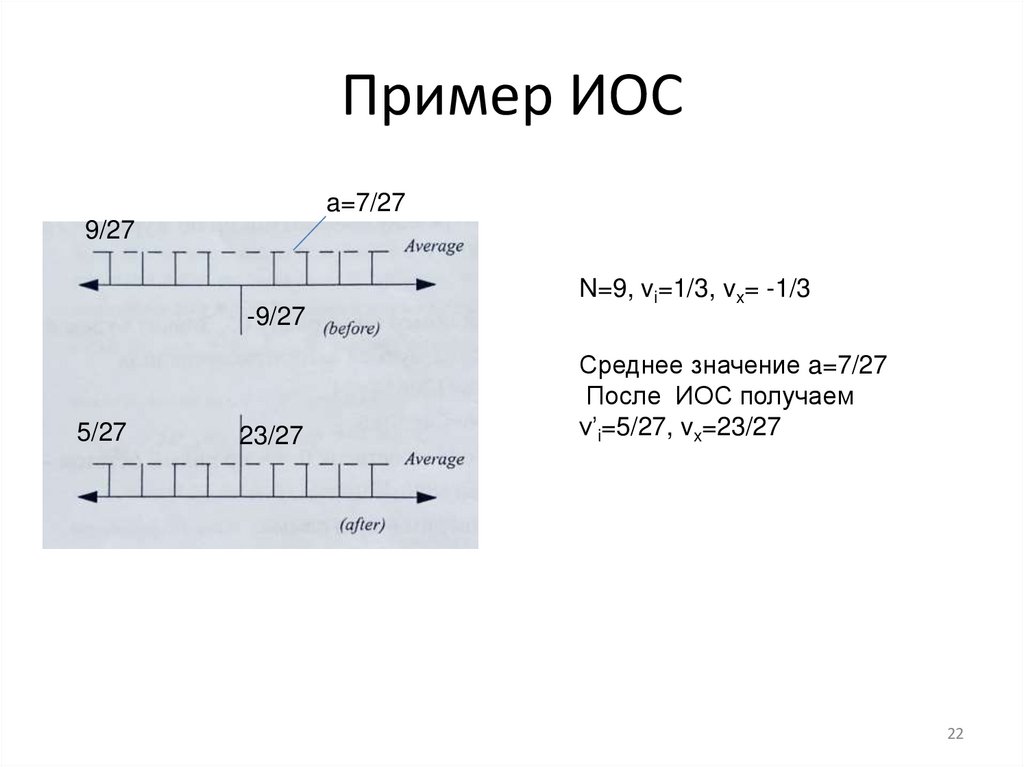
Пример ИОС
a=7/27
9/27
-9/27
5/27
23/27
N=9, vi=1/3, vx= -1/3
Среднее значение a=7/27
После ИОС получаем
v’i=5/27, vx=23/27
22

22. Пример ИОС

Примеры применения процедуры ИОС
при разны N=2n
n=7
n=8
n=9
n=10
23

23. Примеры применения процедуры ИОС при разны N=2n

Этапы алгоритма Гровера
1. Создаем регистр из n кубитов
и устанавливаем все
(n)
разряды в состояние 0 0
2. Применяем преобразование Адамара, получаем состояние
каждой ячейки
1
1
(0 1)
2
- равновероятное состояние.
3. Находим значение функции f(x), применяя оператор
U ( 1)
f ( x)
(при х=х0 f(x0)=1 и U=-1, при других х f(x)=0 и U=1.
Если U=1, то ячейка остается в исходном состоянии, если
U=-1, то изменяет состояние U 1 ( 0 ( 1) 1 ( 1) ) 1 ( 0 1 )
f ( x)
1
2
f ( x)
2
4. Все состояния равновероятные, но одно из них противоположное другим состояниям. Нужно повысить его вероятност
Применяем метод усиления амплитуды (инверсии относительн
среднего.)
24

24. Этапы алгоритма Гровера

Пример алгоритма Гровера
• Задана булева функция от n аргументов
f ( x0 , x1 , , xn ) , которая принимает значение 1
только при одном наборе аргументов.
Нужно найти это состояние.
Решение.
1 этап. Подготавливает начальное состояние
0 0,0, .0 , т.е. все ячейки квантового
регистра устанавливаются в состоянии 0. Или
все кубиты в нулевом состоянии.
0 0 x0 1 x1
2n 1 x2n 1 1 x0 0 x1
0 x2n 1
26

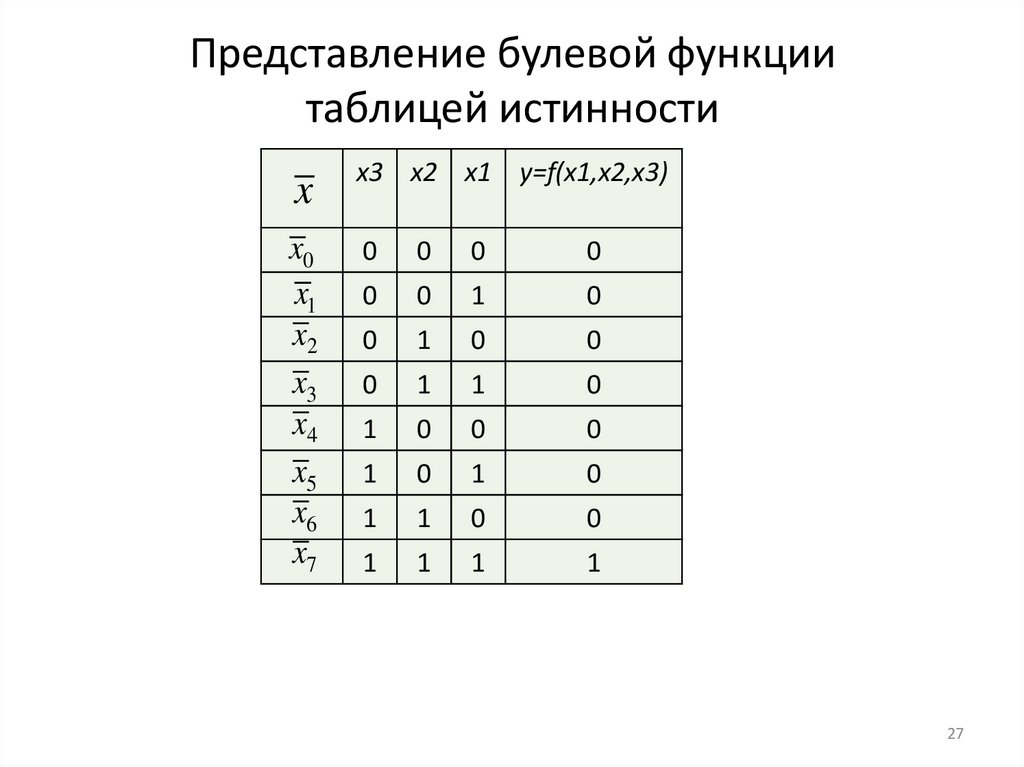
25.

Представление булевой функции
таблицей истинности
x
x0
x1
x2
x3
x4
x5
x6
x7
x3 x2 x1 y=f(x1,x2,x3)
0
0
0
0
0
0
1
0
0
1
0
0
0
1
1
0
1
0
0
0
1
0
1
0
1
1
0
0
1
1
1
1
27

26. Пример алгоритма Гровера

Далее рассмотрим преобразование для функции от
3-х аргументов
• 2 этап. Приготавливаем смесь
равновероятных состояний 1 H3 0
1
1
1
1
1 1
2 2 1
1
1
1
1 1 1 1 1 1 1 1 0,354
1 1 1 1 1 1 1 0 0,354
1 1 1 1 1 1 1 0 0,354
1 1 1 1 1 1 1 0 0,354
1 1 1 1 1 1 1 0 0,354
1 1 1 1 1 1 1 0 0,354
1 1 1 1 1 1 1 0 0,354
1 1 1 1 1 1 1 0 0,354
Состояние 1 является суперпозицией 2n возможных
состояний системы из n кубитов.

27. Представление булевой функции таблицей истинности

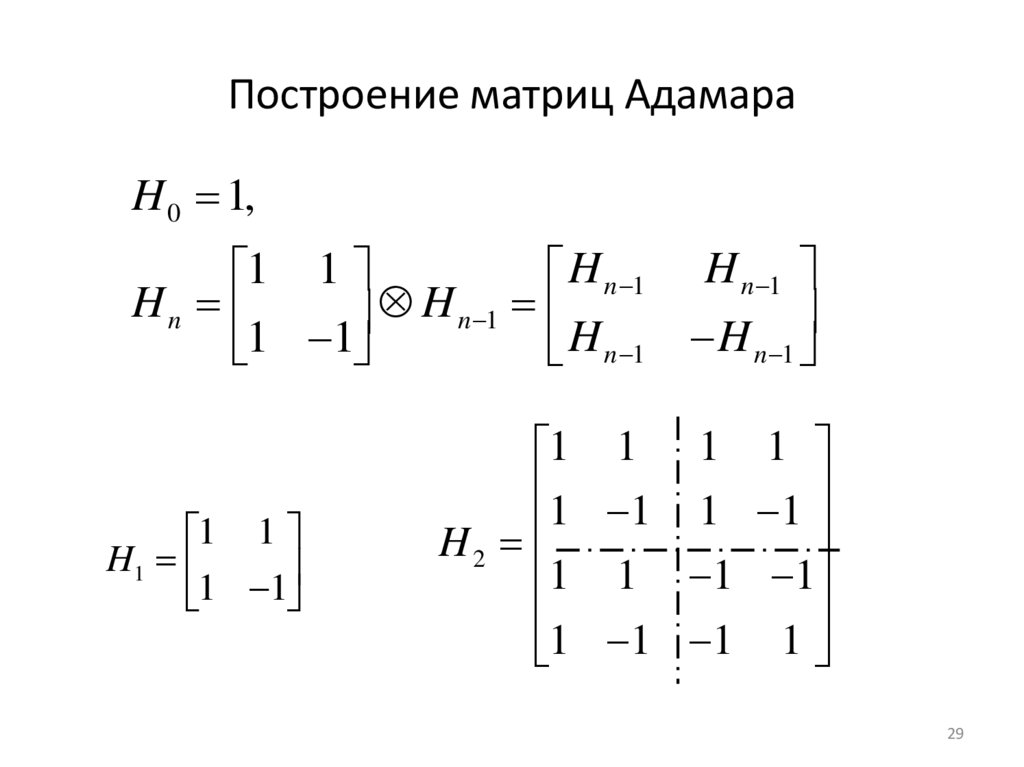
Построение матриц Адамара
H 0 1,
H n 1 H n 1
1 1
Hn
H n 1
H
H
1
1
n 1
n 1
1 1
H1
1
1
1 1 1 1
1 1 1 1
H2
1 1 1 1
1 1 1 1
29

28. Далее рассмотрим преобразование для функции от 3-х аргументов

3 этап. Несколько раз применяем оператор
G RU f
2 G G 1
1 f (000)
0
Uf
0
0
1
f (001)
0
1 0 0 0 0 0 0 0
0
1
0
0 0
1
0
1
0
0 0
0
1
0
f (111)
1
0
1 0
0
1 0
0 0 0 0 0 0 0 1
(пустые места в матрице нули)
30

29. Построение матриц Адамара

1 n 1 1 1 n 1
2
2
1
1 n 1 1
n 1
2
2
R
1 n 1
1 n 1
2
2
1
1
1
1
1
1
3 4 1
4
4
4
4
4
4
4
1
1
3 4
4
4
1
1 n 1 1
3 4
4
4
2
1
1 n 1 1
3 4
4
2 4
1
1
3
4
4
4
1 n 1 1 1
1
3
4
2
4
4
1
1
3 4
4
4
1
1
1
1
1
1
1
3 4
4
4
4
4
4
4
4
Так называемый оператор диффузии
31

30. 3 этап. Несколько раз применяем оператор

Результаты преобразования
0,177
0, 088
0.305
0,177
0,
088
0.305
0,177
0, 088
0.305
0,177
0,
088
0.305
GG
GGG
G 1
1
1
0,177
0, 088
0.305
0,177
0,
088
0.305
0,177
0, 088
0.305
0,884
0,972
0,575
Оптимальное число применений оператора G n раз.
4 2
Состояние соответствующее решению уравнения
f(x)=1, будет иметь максимальную амплитуду и может появиться в
процессе измерения с максимальной вероятностью. Вероятность
получить неправильный результат в алгоритме Гровера оценивается как
O(1/2n).
n /2
O
(2
) операций.
Решение задачи алгоритмом Гровера требует
n 1
Классический переборный алгоритм требует O(2 ) операций.
32

31.

Выводы
• В случайной(неотсортированной) базе данных с N
записями обычный компьютер будет в среднем
делать N / 2 поисковых попыток прежде чем он
обнаружит искомую запись.
• Квантовый компьютер сможет найти запись в
случайной базе данных гораздо быстрее чем
классический компьютер.
• Для поиска на квантовом компьютере в той же
базе данных размера N потребуется всего N
попыток (алгоритм Гровера)
33

32. Результаты преобразования

34

33. Выводы

1. Принцип построения КС РША 1978г.
Формирование пар открытых/закрытых ключей для КС РША
Каждый пользователь КС РША, допустим А, выполняет следующие
операции для формирования пары ключей:
1) генерирует пару простых чисел p и q;
2) вычисляет М = p ∙ q и функцию Эйлера M p 1 q 1 ;
3) генерирует e, где 1 e
, такое что
gcd e,; 1
4) находит число d e 1 mod , т. е. решение уравнения e d 1mod (; M )
5) выбирает числа e, М как свой открытый ключ, а d – как свой
секретный ключ.

34.

Квантовый компьютер и
криптосистема РША
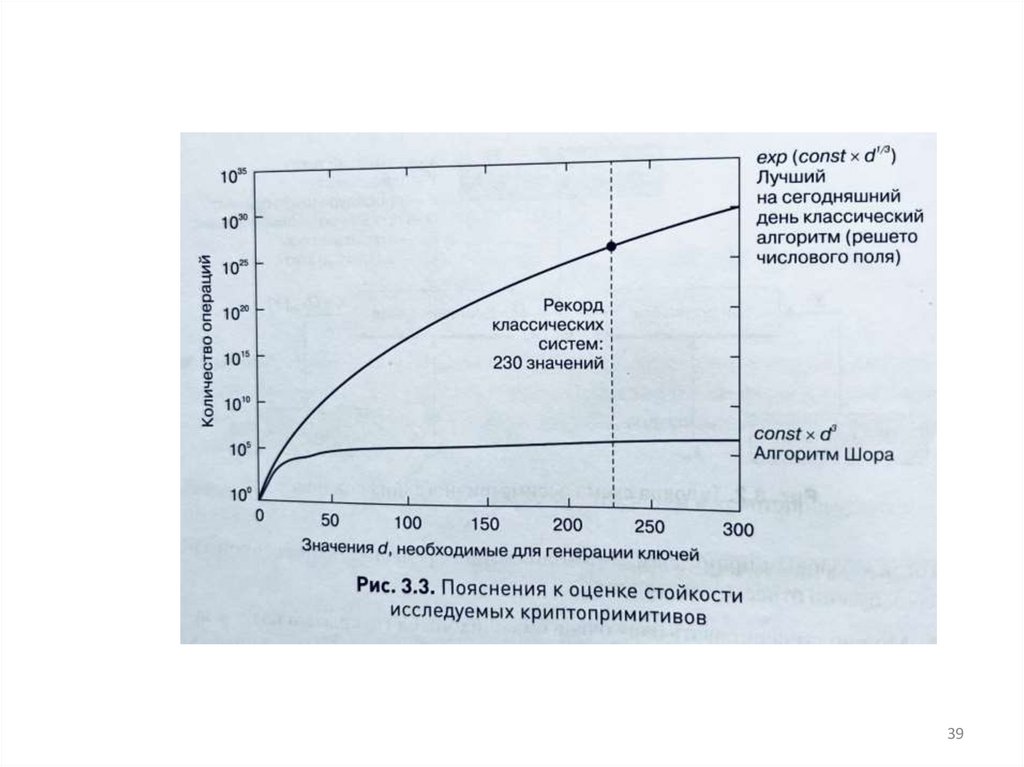
• В ранних криптостойких системах использовались
целые числа с 400 более двоичными числами.
(1994г.)
• На компьютере 1994г. потребуется~109 лет для
разложения такого числа на множители.
• Квантовый компьютер, равный по скорости счета
такому компьютеру, справится с этой задачей за
секунды (алгоритм Шора)
37

35.

Пример длинного числа
p
q
n
Стойкость алгоритма РША основывается на вычислительной
сложности решения задачи факторизации модуля n=nq
38

36. Криптосистема РША

39

37. Квантовый компьютер и криптосистема РША

Идея алгоритма Шора
Дано М=pq, нужно найти p и q
40

38. Пример длинного числа

Пример факторизации на основе поиска
периода
41

39.

• В алгоритме Шора задача факторизации
M=pq сводится к задаче нахождения
периода r функции a x mod M . Наименьшее
значение х, при котором a x mod M 1
называется показателем a по модулю М.
42

40. Идея алгоритма Шора

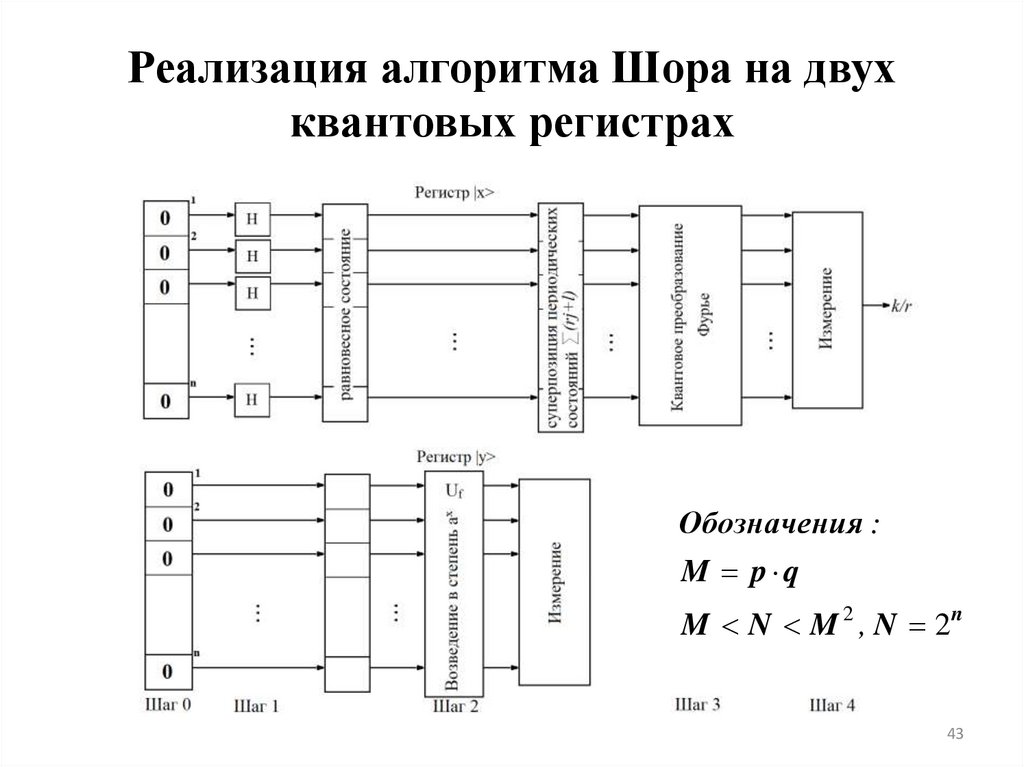
Реализация алгоритма Шора на двух
квантовых регистрах
Обозначения :
M p q
M N M 2 , N 2n
43

41. Пример факторизации на основе поиска периода

Этапы алгоритма Шора
0. Подготовительный этап. Установка регистров в нулевое
состояние.
1. Перевод регистров в равновесное состояние.
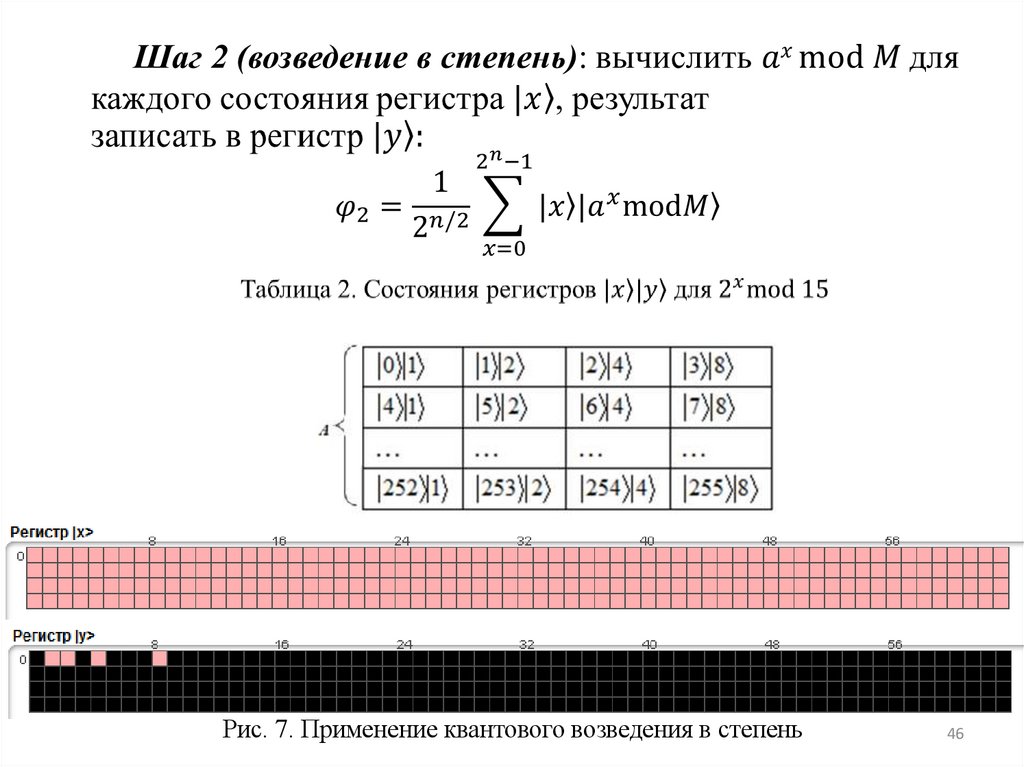
2. Вычисление степеней аx в регистре Y, измерение
состояния регистра.
3. Предвычисление периода с помощью квантового
преобразования Фурье.
4. Вычисление периода на основе подходящих дробей.
(на обычном компьютере)
44

42.

Рис. 5. Инициализация регистров
1 Hn 0 0
Рис. 6. Применение преобразования Адамара к регистру |x>
45

43. Реализация алгоритма Шора на двух квантовых регистрах

Рис. 7. Применение квантового возведения в степень
46

44. Этапы алгоритма Шора

Измерение состояния регистра Y
y 8
Например, фиксированному состоянию
Последовательность значений x
2
1
А 1
соответствует
A
3 7 11 ... 8 A 1 r j l 8
1
j 0
где А наибольшее целое меньшее, чем ( N l ) / r , A N / r .
Состояние рег. Х при
измеренном сост. рег.. У
l
xi ji r l ,
r

45.

Вычисление периода
Из этого состояния мы хотим выделить информацию о периоде r.
Временно сделаем предположение, что l при разных испытаниях принимает
одно и тоже значение. Пусть мы провели 3 испытания и получили три копии 2
x1 j1r l ,
Далее находим
x2 j2 r l , x3 j3r l ,
x1 x2 ( j1 j2 )r , x1 x3 ( j1 j3 )r
Поскольку j равновероятны, то с высокой вероятностью gcd(j1 j2 , j1 j3 ) 1
Поэтому период легко вычисляется так как
gcd(x1 x2 ,x1 x3 ) gcd((j1 j2 )r,( j1 j3 )r) r
Пример:
x1 27, x2 15, x3 7,
gcd(x1 x2 , x1 x3 ) gcd(( 27 15 ),( 27 7 ))
gcd( 12 , 20 ) 4
К сожалению, l изменяется случайно (определяется случайным измерением
регистра Y , поэтому принципиально необходимо применение квантового
преобразования Фурье, устраняющего этот недостаток.
48

46.

Случай, когда l 0
Рассмотрим сначала частный случай, когда r делит N нацело. Тогда A N / r
N 1
Запишем состояние регистра x в следующем виде l f (x) x
x 0
где
Это λ
f (x) r / N , если x l кратно r ,
f (x) 0, если x l не кратно r
Тогда состояние регистра можно переписать так l
f(x)
l
r
r
r
r N / r 1
jr l
N j 0
амплитуда
r/N
x
Свойство временного сдвига преобразовагия Фурье
Пусть известно преобразоваие Фурье функции f(t): f (t ) F ( ) ,
Тогда для функции f(t-l) преобразование Фурье имеет вид
f (t l ) F ( )e i l
Из данного свойства следует, что при временном сдвиге функции на l
F ( )
ее амплитудный спектр
не изменяется. Изменения происходят
только в фазовом спектре на величину
.
Для квантовых вычислений общий сдвиг фазы на амлитуды состояний не
влияет .

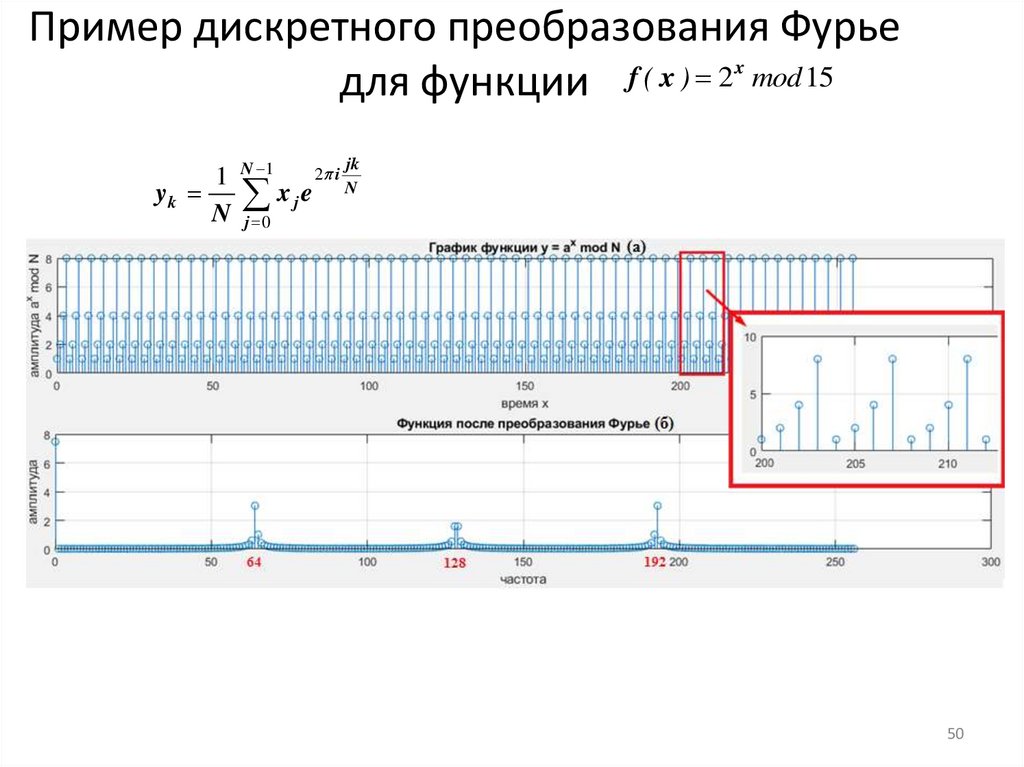
47.

Пример дискретного преобразования Фурье
x
f
(
x
)
2
mod 15
для функции
2 i
1 N 1
yk
x je N
N j 0
jk
50

48. Вычисление периода

Квантовое преобразование Фурье
DFT l f ( c ) c
Выполняя ДПФ для состояния l , получаем
где амплитуда f ( c )DFT от f (x) N/r
c
r N / r 1
2 i( jr l )c
r N / r 1
jc
lc
f (c)
exp(
)
exp(
2
i
) exp( 2 i )
N j 0
N
N j 0
N / r
N
Используя свойство комплексной функции в показательной форме,
T
jn
T ,n 0 mod T ,
exp 2 i T 0,n 0 mod T можно записать, что в последнем выражении
j
член в квадратных скобках равен нулю за исключением с кратных N/r
поэтому
,
r N
lc
1
lc
N
exp( 2 i )
exp( 2 i ), если c кратно ,
f (c) N r
N
N
r
r
0 , в противном случае .
f(c )
N/r
N/r
0
N
Полагая, c j
r
N/r
амплитуда
N/r
r
r-1
запишем
DFT l
c
1 r 1
jl
N
exp( 2 i ) j
r
r
r
j 0
51

49. Случай, когда

f ( x ) 2 mod 15
Для нашего примера
состояние регистра после
КПФ будет таким, как показано на рисунке, то есть, ненулевые
вероятности имеют состояния 0 , 64 , 128 , 192
x
N
Вероятность какого либо состояния: c j
2
r
N 1
r r
P c 2 exp( 2 ij( rc mod N ) / N )
N j 0
После преобразований можно получить
P c
4 1
2 r
Окончательно мы хотим выделить информацию о периоде r.
Для этого проводится измерение состояния регистра x
Пусть с=64, тогда j/r=64/256=1/4
откуда r=4 - период найден
53

50. Пример дискретного преобразования Фурье для функции

Случай, когда r не делит N
Мы рассмотрели частный случай, когда r делит N нацело,т.е. rc mod N 0
Если от этого условия отказаться, то
r / 2 rc mod N r / 2
(1)
Пусть rc mod N kN r / 2 , тогда условие (1) запишем так
rc kN r / 2
(2)
Разделав обе части (2) на Nr, получим
c k
1
N r 2N
По результатам измерения регистра x мы получили величину c/N,
тогда, используя разложение c/N в цепную дробь, можно рассчитать
подходящую дробь k/r и найти r.
P c 0.4 . Для повышения вероятности проводим
Вероятность успеха
испытания несколько раз с разными значениями a.

51. Квантовое преобразование Фурье

1018
55

52.

Система шифрования Эль-Гамаля 1985г.
Пусть p -простое число; a - примитивный элемент.
Корреспондент А
Создание пары: закрытыйоткрытый ключи
A - генерирует число xA<p,
вычисляет ОНФ
yA=ax (modp).
(SK= xA , PK= yA).
yA передается корр. B.
Корреспондент В
Шифрование сообщения
Пусть корр. B хочет послать корр.А
сообщение m<p.
Генерирует случайное число k<p.
Формирует криптограмму E=(c1c2)
c1=akmodp, c2=m (yA-1)k modp.
Отправляет E корр. А.

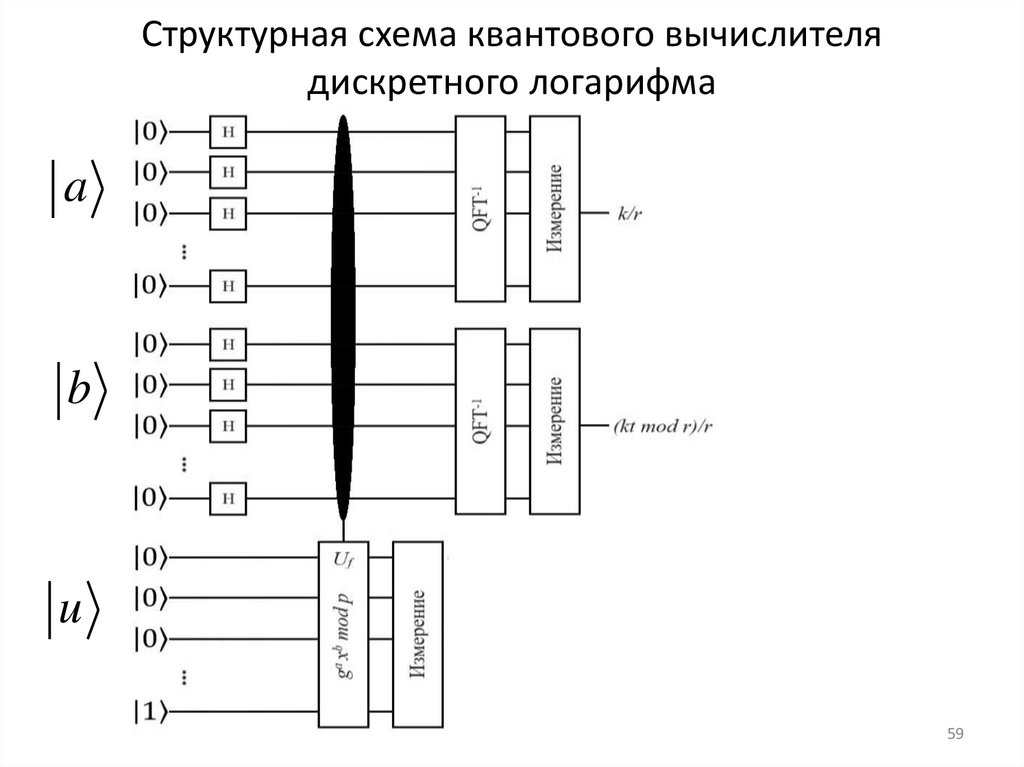
53.

Алгоритм дискретного логарифмирования
Шора на квантовом компьютере
Дискретный логарифм – это математическая задача обращения функции