Алгоритмы линейной обработки последовательности чисел без дополнительной памяти. Тема 3.1.2

1. Тема 3.1.2 Алгоритмы линейной (однопроходной) обработки последовательности чисел без использования дополнительной памяти,

зависящей от длины последовательности

2.

Повторение — алгоритмическая конструкция, представляющая
собой последовательность действий, выполняемых многократно.
Алгоритмы, содержащие конструкцию повторения, называют
циклическими или циклами. Последовательность действий,
многократно повторяющаяся в процессе выполнения цикла,
называется телом

3.

В зависимости от способа организации повторений
различают три типа циклов:
1) Цикл с заданным условием продолжения работы
2) Цикл с заданным условием окончания работы
3) Цикл с заданным числом повторений

4.

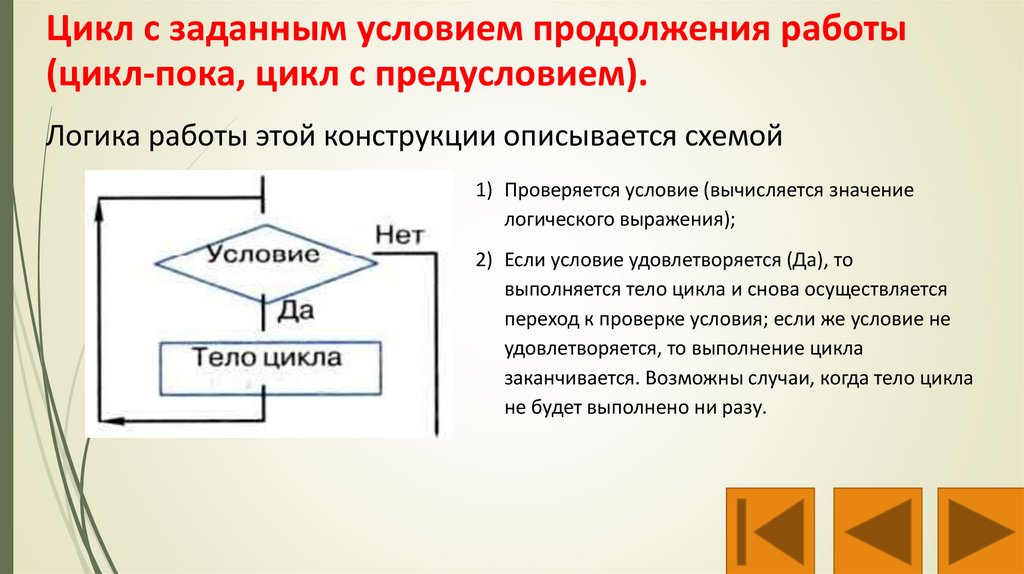
Цикл с заданным условием продолжения работы
(цикл-пока, цикл с предусловием).
Логика работы этой конструкции описывается схемой
1) Проверяется условие (вычисляется значение
логического выражения);
2) Если условие удовлетворяется (Да), то
выполняется тело цикла и снова осуществляется
переход к проверке условия; если же условие не
удовлетворяется, то выполнение цикла
заканчивается. Возможны случаи, когда тело цикла
не будет выполнено ни разу.

5.

Пример
Требуется, не пользуясь операцией деления, получить частное q и остаток r от деления
натурального числа х на натуральное число у.
Представим операцию деления как последовательные вычитания
делителя из делимого. Причём вычитать будем до тех пор, пока
результат вычитания не станет меньше вычитаемого (делителя). В
этом случае количество вычитаний будет равно частному от
деления q, а последняя разность — остатку от деления r.

6.

Исполним этот алгоритм для х = 23 и у = 5.

7.

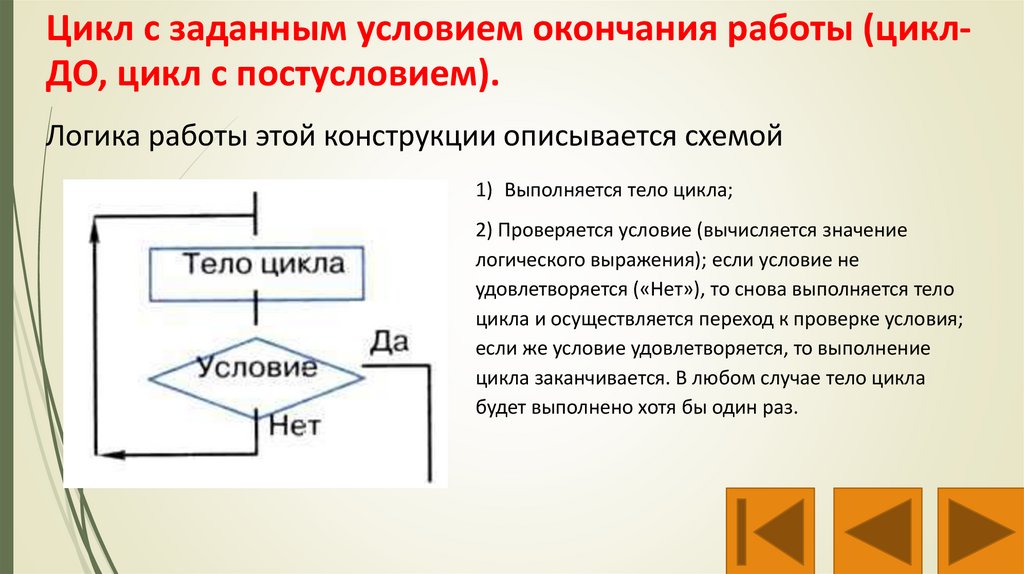
Цикл с заданным условием окончания работы (циклДО, цикл с постусловием).
Логика работы этой конструкции описывается схемой
1) Выполняется тело цикла;
2) Проверяется условие (вычисляется значение
логического выражения); если условие не
удовлетворяется («Нет»), то снова выполняется тело
цикла и осуществляется переход к проверке условия;
если же условие удовлетворяется, то выполнение
цикла заканчивается. В любом случае тело цикла
будет выполнено хотя бы один раз.

8.

Пример
Вычислим значение переменной b согласно следующему алгоритму:

9.

Цикл с заданным числом повторений (цикл-ДЛЯ, цикл
с параметром).
Логика работы этой конструкции описывается схемой
1) Параметру цикла присваивается начальное значение;
2) Параметр цикла сравнивается с конечным значением;
если параметр цикла не превышает конечное значение, то
выполняется тело цикла, увеличивается значение
параметра цикла на шаг и снова осуществляется проверка
параметра цикла; если же параметр цикла превышает
конечное значение, то выполнение цикла заканчивается.

10.

Если величина шага в цикле с параметром равна единице, то шаг
не указывают. Мы ограничимся рассмотрением именно таких
циклов.
В отличие от двух предыдущих конструкций (цикл-ПОКА, циклДО) цикл-ДЛЯ имеет строго фиксированное число повторений,
что позволяет избежать зацикливания, т. е. ситуации, когда тело
цикла выполняется бесконечно.

11.

Пример
Вычислить сумму n чисел.
При вычислении суммы n слагаемых действие сложение
повторится n раз.
Перечислим действия алгоритма:
1) Переменной s присвоить значение 0.
2) Организовать цикл, количество повторений которого совпадает
с количеством слагаемых. В цикле получить значение очередного
слагаемого и добавить его к сумме.
Используя этот алгоритм, решим частную задачу: вычислить
сумму первых 10 чисел натурального ряда.

12.

S
a
S=S+a
Шаг 1
0
1
1
Шаг 2
1
2
3
Шаг 3
3
3
6
Шаг 4
6
4
10
Шаг 5
10
5
15
Шаг 6
15
6
21
Шаг 7
21
7
28
Шаг 8
28
8
36
Шаг 9
36
9
45
Шаг 10
45
10
55

13.

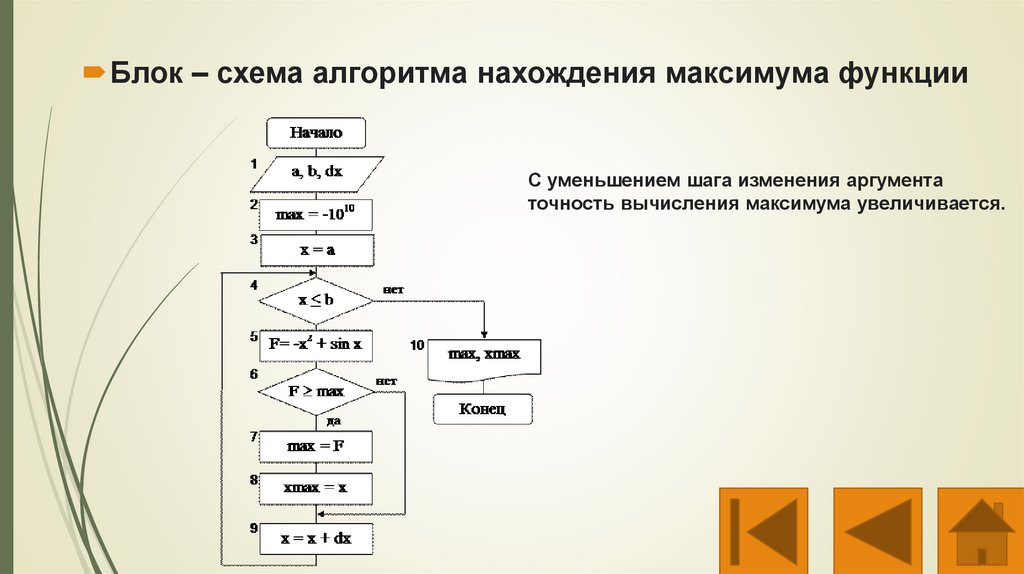
Простейшая задача нахождения максимума функции решается по
следующему алгоритму:
1.Задаются границы a и b, в пределах которых имеется максимум функции.
2.Интервал [a,b] разбивается на определенное количество шагов.
3.Функция табулируется в пределах заданного интервала, и каждое
вычисленное значение функции сравнивается с максимальным
(заданным до начала табулирования).
4.Находится максимальное значение функции на заданном интервале с
определенным шагом и выводится на печать.

14.

Блок – схема алгоритма нахождения максимума функции
С уменьшением шага изменения аргумента
точность вычисления максимума увеличивается.