Лекция № 10 Тема 4 Основы теории графов

1. Кафедра системы сбора и обработки информации

ВОЕННО-КОСМИЧЕСКАЯ АКАДЕМИЯ ИМЕНИ А.Ф. МОЖАЙСКОГО
Кафедра системы сбора и обработки информации
Дискретная математика
Лекция № 10
Тема 4 Основы теории графов
Андрушкевич С.С..

2.

2
Лекция № 10. Основные понятия теории графов
Цель: ознакомиться с основными понятиями теории графов и
с матрицами,связанными с графами. Научится по матрицам
смежности строить граф и определять его характеристики
Учебные вопросы:
1.
Основные определения
2.
Маршруты, связность, циклы и разрезы
3.
Ориентированные графы
4.
Матрицы, ассоциированные с графом

3. Учебный вопрос №1

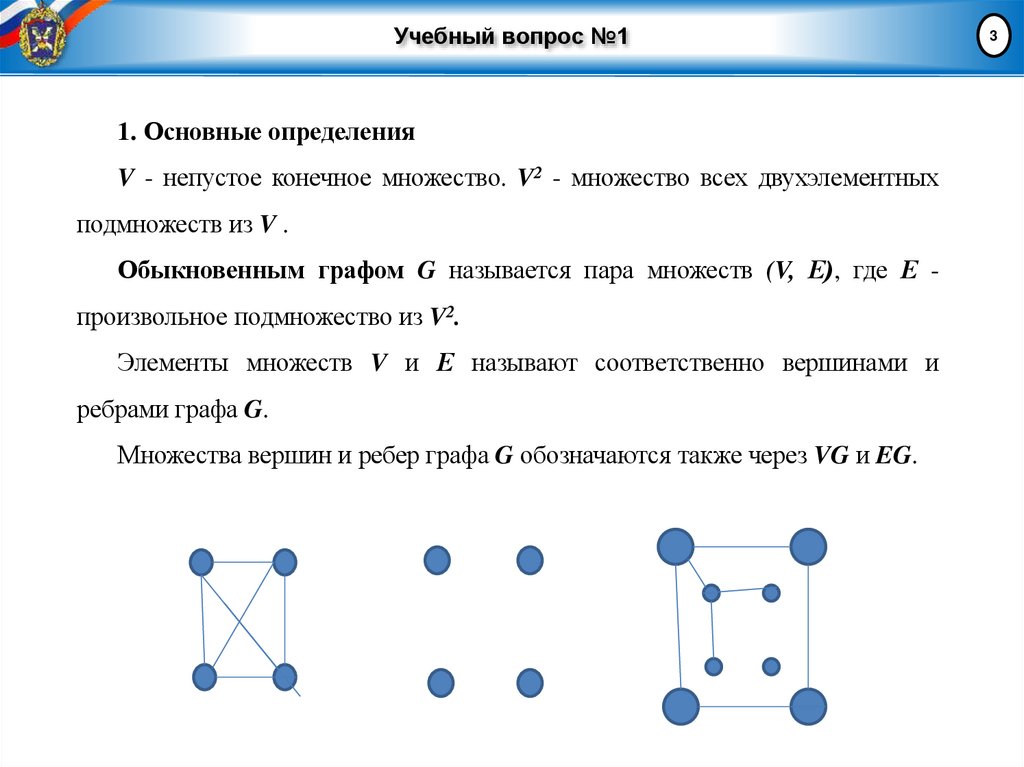
1. Основные определения
V - непустое конечное множество. V2 - множество всех двухэлементных
подмножеств из V .
Обыкновенным графом G называется пара множеств (V, Е), где Е произвольное подмножество из V2.
Элементы множеств V и Е называют соответственно вершинами и
ребрами графа G.
Множества вершин и ребер графа G обозначаются также через VG и EG.
3

4. Учебный вопрос №1

4
Граф G, имеющий n вершин, называют n-графом;
Если при этом G содержит m ребер, то G это (n, т) граф.
Если е = иv - некоторое ребро данного графа, то вершины и, v
называются смежными; При этом и, v - концевые вершины ребра е.
Ребро е и вершина v инцидентны, если v - концевая вершина
для е.
Ребра е и f называются смежными, если они имеют общую
концевую вершину.
Пусть
G1 = (V1, Е1), G2 = (V2, Е2)- два графа.
Биективное
отображение ѱ : V1 → V2 называется изоморфизмом G1 на G2, если
для любых u, v ∈ V1 число ребер, соединяющих вершины u и v в G1 ,
равно числу ребер, соединяющих ѱ(u) и ѱ(v) в G2 (при u=v число
петель в вершине u равно числу петель в вершине ѱ (u)).

5. Учебный вопрос №1

Графы G1 и G2 изоморфны (G1 ≅ G2), если существует изоморфизм G1 на G2.
Отображение ѱ, определенное правилом ѱ (иi) = vi (1 ≤ i ≤ 6), очевидно,
является изоморфизмом.
Степенью вершины v называется число ребер, инцидентных этой вершине,
причем каждая петля учитывается дважды. Степень вершины v обозначается через