Понятие множества Лекция № 1

1.

Раздел 1. Элементы теории множеств
Тема 1.1.
Множества. Способы задания множеств
Понятие множества
Лекция № 1

2. Понятие множества

Множеством называется совокупность (набор) однородных
различаемых элементов.
Создатель теории множеств немецкий математик Георг Кантор определил
множество как «объединение в одно целое объектов, хорошо различаемых
нашей интуицией или нашей мыслью». Он же сформулировал это короче:
«множество - это многое, мыслимое нами как единое».
Основоположник теории множеств
немецкий математик Георг Кантор
(1845-1918)

3.

С понятием множества человек встречается, прежде всего
тогда, когда по какой-либо причине приходится объединять по
некоторому признаку в одну группу какие-то объекты. Далее
эта группа или совокупность рассматривается как единое
целое.
Например, множество букв, множество определенных чисел,
группа людей, объединенных по какому-либо признаку.
Множества принято обозначать заглавными латинскими
буквами: A, B, C,…
Объекты, которые образуют множество, называют
элементами множества и для обозначения элементов
используют, как правило, малые буквы латинского алфавита:
a, b, c, …

4.

Примеры множеств
множество учащихся в данной аудитории;
множество людей, живущих на нашей планете в
данный момент времени;
множество точек данной геометрической фигуры;
множество чётных чисел;
множество корней уравнения х2 - 5х + 6 = 0;
множество чисел, которые делятся на 5.

5.

Дни недели
понедельник
вторник
среда
пятница
суббота

6.

Музыкальные инструменты

7.

Цвета

8.

Как можно назвать представленное множество?

9.

Объекты, из которых состоит множество, называются его
ЭЛЕМЕНТАМИ.
Если элемент x принадлежит множеству X, то записывается
x Х ( - принадлежит).
В противном случае, если a не принадлежит множеству А,
используется обозначение , т.е. a A.
Если множество А является частью множества В, то записывают
А В ( - содержится).
Пусть даны множества A = {1,2,3,4,5,6} и B = {1,3,5}.
Тогда можно записать:
элемент 2 принадлежит множеству А:
2 A,
элемент 2 не принадлежит множеству B:
2 B,
множество B включено в множество А:
B A.

10. Способы задания множеств

1. Множество может быть задано перечислением всех его
элементов или списком. В этом случае элементы множества
записывают внутри фигурных скобок, например:
A = {студент А., рабочий Л., школьник М.};
B = {а, е, ё, и, о, у, э, ю, я, ы}.
2. Множество может быть задано описанием свойств его
элементов. Чаще всего при этом используют запись, которую читают
следующим образом: «A есть множество элементов b таких, что для
них выполняется свойство B», например:
A = {a | а – четное натуральное число};
B = {b | b – натуральное число, кратное 3}.
3. Множество можно задать порождающей процедурой,
например:
А = {a | a = 2k, k - любое натуральное число}.

11. Например, перечислением заданы следующие множества:

А = {1,2,3,5,7} - множество чисел
Х = {x1, x2, ..., xn} - множество некоторых элементов x1, x2, ..., xn
N = {1, 2, ..., n} - множество натуральных чисел
Z = {0, ±1, ±2, ..., ± n} - множество целых чисел
Например, множество задано условием M = {х | х2 - 5х + 6 = 0}.
Чтобы определить его элементы, необходимо решить квадратное
уравнение:
х2 - 5х + 6 = 0;
D = b2 - 4ac = (-5)2 - 4 1 6 = 25 – 24 = 1 > 0;
x1
b D 5 1 6
3
2a
2 1
2
x2
b D 5 1 4
2
2a
2 1
2
Следовательно, множество M = {2, 3}.

12.

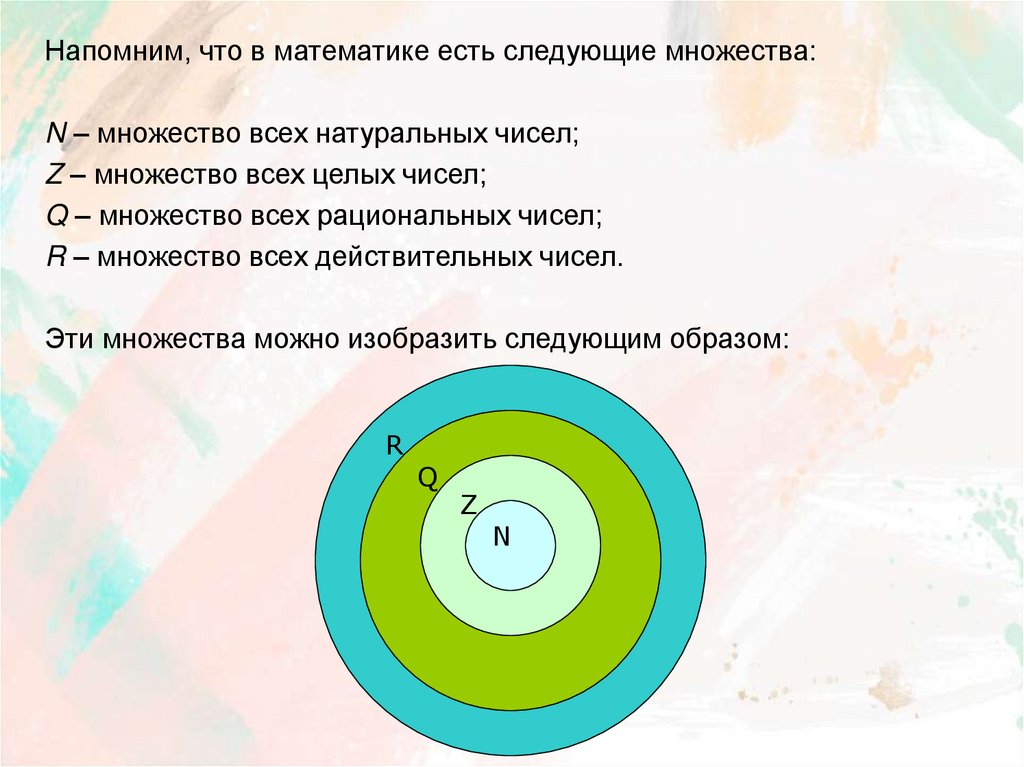
Напомним, что в математике есть следующие множества:
N – множество всех натуральных чисел;
Z – множество всех целых чисел;
Q – множество всех рациональных чисел;
R – множество всех действительных чисел.
Эти множества можно изобразить следующим образом:
R
Q
Z
N

13. Рассмотрим пример

Мы говорим, что число 5 натуральное, т.е. утверждаем, что
число 5 принадлежит множеству натуральных чисел.
Символически принадлежность множеству записывается с
помощью знака . В данном случае символическая запись будет
такой: 5 N. Читается: “5 принадлежит множеству натуральных
чисел”.
А вот число 5,2 не принадлежит множеству натуральных чисел,
т.к. не является натуральным числом.
Символически отношение “не принадлежит” записывается с
помощью знака . Таким образом, здесь имеем: 5,2 N. Читается:
“5,2 не принадлежит множеству натуральных чисел”.