Определение параметров аддитивных скремблеров. Лекция 9

1. Дисциплина: ОТА – СД 303-1-53

Раздел 1. Идентификация помехоустойчивых
кодов и скремблеров
Тема 4. Идентификация скремблеров.
Лекция 9. Определение параметров аддитивных
скремблеров
Занятия проводят:
- Хмельков Андрей Николаевич
- Минеев Владислав Анатольевич
- Смоляков Михаил Сергеевич

2.

Дисциплина: СД 302-1-53. Оперативно-технический анализ.
(ОТА ИПКиС)
Тема 4. Идентификация скремблеров.
Лекция 9. Определение параметров аддитивных
скремблеров (2 час).
План
1. Идентификация аддитивного скремблера при полной
априорной неопределенности.
2. Идентификация аддитивного скремблера при
частичной (доразведка) априорной неопределенности.
2

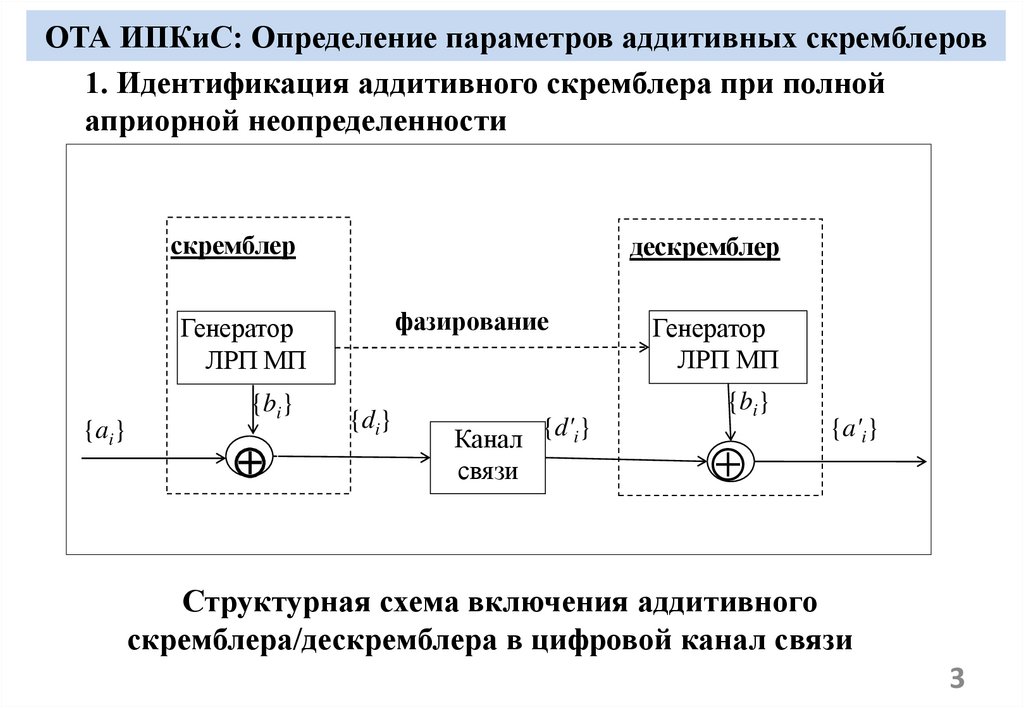
3. ОТА ИПКиС: Определение параметров аддитивных скремблеров

1. Идентификация аддитивного скремблера при полной
априорной неопределенности
скремблер
дескремблер
фазирование
Генератор
ЛРП МП
{ai}
{bi}
{di}
Канал {d'i}
связи
Генератор
ЛРП МП
{bi}
{a'i}
Структурная схема включения аддитивного
скремблера/дескремблера в цифровой канал связи
3

4. ОТА ИПКиС: Определение параметров аддитивных скремблеров

1. Идентификация аддитивного скремблера при полной
априорной неопределенности (продолжение)
Для идентификации (определения параметров) аддитивного
скремблера по фрагменту цифрового потока необходимо определить:
- характеристический многочлен – f(x);
- начальную фазу (начальное заполнение генератора ЛРП МП) – НФ.
4

5. ОТА ИПКиС: Определение параметров аддитивных скремблеров

1. Идентификация аддитивного скремблера при полной априорной
неопределенности
Основа идентификации
- детерминированность (сосредоточенная или распределенная)
скремблируемого ЦП:
наличие в ЦП элементов синхронизации, синхровставок, флагов,
«молчащих» каналов и т.д.
Базовый АПП-алгоритм
(идентификация аддитивного скремблера по периодической
последовательности)
Допущения (идеальная модель идентификации):
- известен период k следования детерминированных элементов в
скремблируемом ЦП;
- известна степень характеристического многочлена скремблера (n);
- вероятность ошибки на бит – pb = 0;
- НОД (2n-l,k) = 1.
5

6. ОТА ИПКиС: Определение параметров аддитивных скремблеров

1. Идентификация аддитивного скремблера при полной априорной
неопределенности (продолжение)
Базовый АПП-алгоритм:
п.1. Демультиплексировать ЦП {di} на k подпотоков:
{dk(i-1)+j} (j = 1, k ).
Сформировать дополнительно k инверсных подпотоков, учитывая, что
значение детерминированного элемента может быть равно 1.
п.2. Построить 2k систем линейных двоичных алгебраических
уравнений:
bk j ... bk ( n 1) j cn( k ) bkn j
bj
b
( k ) b
b
...
b
2k j
kn j
k j
cn 1 k ( n 1) j
...
...
...
... ... ...
(k )
b
b
...
b
b
kn j
2 k ( n 1) j c1
k ( n 1) j
2 kn j
Примечание: нумерация элементов {bi} соответствует нумерации
элементов заскремблированного ЦП {di}, начиная с первого элемента.6

7. ОТА ИПКиС: Определение параметров аддитивных скремблеров

1. Идентификация аддитивного скремблера при полной априорной
неопределенности (продолжение)
п.3. Решить 2k систем линейных двоичных алгебраических уравнений.
В результате решения получим 2k предполагаемых характеристических
многочленов ЛРП МП {bki+j} – f(j)k(x).
п.4. Проверить полученное решение на достоверность.
п.5. Если проверка на достоверность хотя бы для одного решения
выполнилась, то перейти к п.7.
п.6. Аддитивный скремблер при заданных допущениях не
идентифицирован.
п.7. Вычислить обратный коэффициент выборки k .
п.8. Сформировать ЛРП МП с характеристическим многочленом f(j)k(х) и
начальной фазой: bjbk+j,...bk(n-1)+j.
7

8. ОТА ИПКиС : Определение параметров аддитивных скремблеров

1. Идентификация аддитивного скремблера при полной априорной
неопределенности (продолжение)
п.9. Выбрать из полученной последовательности 2n элементов, начиная
с первого, с коэффициентом выборки k .
В результате получим 2n элементов ЛРП МП скремблера {bi},начиная с
j-того элемента.
п.10. Построить систему линейных двоичных алгебраические
уравнений:
.
b1
b
2
...
bn
b2
b3
...
bn 1
... bn cn bn 1
... bn 1 cn 1 bn 2
...
... ... ...
... b2 n 1 c1 b2 n
8

9. ОТА ИПКиС : Определение параметров аддитивных скремблеров

1. Идентификация аддитивного скремблера при полной априорной
неопределенности (продолжение)
п.11. Решить систему линейных двоичных алгебраических уравнений.
Решением являются коэффициенты при неизвестном
характеристического многочлена аддитивного скремблера f(х).
п.12. Аддитивный скремблер идентифицирован:
- характеристический многочлен f(х);
- начальная фаза bj...bn+j.
Кроме того:
- определена позиция (j) первого детерминированного элемента, с
которого можно проводить дескремблирование ЦП {bi} с полученной
начальной фазой;
- определено значение детерминированного элемента.
9

10. ОТА ИПКиС : Определение параметров аддитивных скремблеров

1. Идентификация аддитивного скремблера при полной априорной
неопределенности (продолжение)
Пояснения к базовому АПП-алгоритму
(проверка решения на достоверность)
Полученное решение системы линейных уравнений должно
удовлетворять следующим требованиям:
- в левой части диагонализированной матрицы должна быть единичная
подматрица;
- cn 1;
- количество членов характеристического многочлена должно быть
нечетным (c0 1),
следовательно, вес крайнего правого столбца диагонализированной
матрицы должен быть четным;
- при пробном дескремблировании на каждой k-той позиции должен
располагаться полученный детерминированный элемент ЦП;
- характеристический многочлен скремблера – примитивный многочлен
10
степени n.

11. ОТА ИПКиС : Определение параметров аддитивных скремблеров

1. Идентификация аддитивного скремблера при полной априорной
неопределенности (продолжение)
Исключение допущений базового АПП-алгоритма
1. Применение алгоритма при неизвестном периоде следования
детерминированных элементов в исходном ЦП.
Необходимо последовательно применять АПП-алгоритм для всех
возможных длин кадров.
2. Применение алгоритма при неизвестной степени
характеристического многочлена.
Необходимо построить систему линейных двоичных алгебраических
уравнений (см. п.2 алгоритма) из расчета:
max{step[f(х)]} = 23.
В ЦСС скремблеры с характеристическими многочленами, степень
которых превышает 23, не применяются.
11

12. ОТА ИПКиС : Определение параметров аддитивных скремблеров

1. Идентификация аддитивного скремблера при полной априорной
неопределенности (продолжение)
В данном случае в диагонализированной расширенной матрице можно
выделить единичную подматрицу размерности n n (где n - степень
характеристического многочлена), начиная с 1-го элемента первой строки.
Причем 23-n строк, расположенных под единичной подматрицей,
должны быть нулевыми.
В примере:
12

13. ОТА ИПКиС : Определение параметров аддитивных скремблеров

1. Идентификация аддитивного скремблера при полной априорной
неопределенности (продолжение)
3. Применение алгоритма, если длины фрагмента анализируемого ЦП не
хватает для формирования под потоков требуемой длины на величину,
равную .
В этом случае система уравнений п.2 алгоритма будет иметь 2 решений,
которые могут быть получены путем до определения последних бит.
Если в результате предварительного отбора все же остается несколько
решений, тогда необходимо анализировать дескремблированный ЦП на
наличие детерминированности.
13

14. ОТА ИПКиС : Определение параметров аддитивных скремблеров

1. Идентификация аддитивного скремблера при полной априорной
неопределенности (продолжение)
Применение АПП-алгоритма при pb 0
Если вероятность искажения элемента декодированного ЦП не равна
нулю (pb 0),
то возможен пропуск решения, вызванный искажением хотя бы одного
из 2n элементов системы линейных двоичных алгебраических уравнений
(п.2 алгоритма):
pпр(1) = 1 – (1 – рb)2n
Для уменьшения вероятности пропуска решения достаточно применить
АПП-алгоритм последовательно на N различных участках ЦП.
Тогда вероятность пропуска:
pпр(N) = [1 – (1 – pb)2n]N
14

15. ОТА ИПКиС : Определение параметров аддитивных скремблеров

1. Идентификация аддитивного скремблера при полной априорной
неопределенности (продолжение)
При ведении радио мониторинга обычно задается допустимая
вероятность пропуска решения рпр.доп.
В этом случае количество участков (N), требуемых для проведения
идентификации, определяется из выражения:
рпр.доп > [1 – (1 – pb)2n]N,
и
N > [lg(рпр.доп)]/lg[1 – (1 – pb)2n]
Если учесть, что n ≤ 23 и pb ≤ 10-3, тогда:
N = -0,74·lg(рпр.доп) ,
где * - ближайшее большее целое.
АСК-способ является частным случаем АПП-способа.
15

16. ОТА ИПКиС : Определение параметров аддитивных скремблеров

1.1. Обратный коэффициент выборки
Задана ЛРП МП {bi} с характеристическим многочленом f(x) и из нее
выбирается каждый k-ый элемент. Тогда последовательность
элементов {bki} (k 1, 2n 1) будет также ЛРП МП, но с
характеристическим многочленом fk(х) при условии, что
НОД (k, 2n-1)=1 (см. свойство 3 ЛРП
МП).
Обратный коэффициент выборки k позволяет восстановить ЛРП МП
ki .
{bi} по ЛРП МП {bki} путем выбора
из
нее
элементов
с
номерами
Справедливо тождество: k k 1 mod(2n 1).
Тогда обратный коэффициент выборки соответствует наименьшему
целому
n
1 (2 1)t
.
k
k
t 1, n :
t выбирается из диапазона
16

17. ОТА ИПКиС : Определение параметров аддитивных скремблеров

1.1. Обратный коэффициент выборки (продолжение)
Пример. Сформирована k-ичная выборка с k=3 из исходной ЛРП МП
{bi} с периодом L=31.
Вычислить обратный коэффициент выборки k для восстановления
исходной ЛРП МП ({b3i} {bi}).
L и k взаимно простые
числа: НОД(31, 3)=1.
Для определения k построим таблицу:
k
Следовательно
k= 21.
17

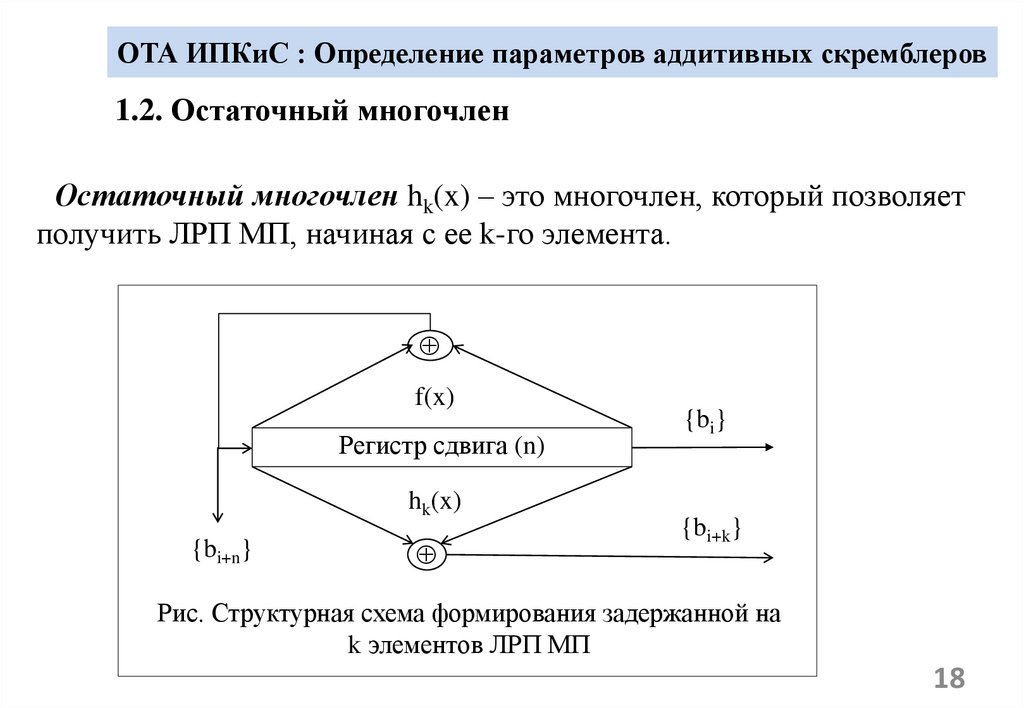
18. ОТА ИПКиС : Определение параметров аддитивных скремблеров

1.2. Остаточный многочлен
Остаточный многочлен hk(x) – это многочлен, который позволяет
получить ЛРП МП, начиная с ее k-го элемента.
f(x)
Регистр сдвига (n)
hk(x)
{bi+n}
{bi}
{bi+k}
Рис. Структурная схема формирования задержанной на
k элементов ЛРП МП
18

19. ОТА ИПКиС : Определение параметров аддитивных скремблеров

1.2. Остаточный многочлен (продолжение)
Остаточный многочлен hk(x) - это есть двойственный многочлен к
остатку от деления одночлена хk-1 на многочлен fД(x) (двойственный
характеристическому многочлену f(x) ЛРП МП).
Пример 1. ЛРП МП задана характеристическим многочленом f(x) = x5
+ x3 + 1.
Вычислить остаточной многочлен h21(х) для получения ЛРП МП,
начиная с 21-го элемента.
Найдем остаток от деления x20/fдв(x):
19

20. ОТА ИПКиС : Определение параметров аддитивных скремблеров

1.2. Остаточный многочлен (продолжение)
x20
│
x5+x2+1
x20+ x17+ x15
x15+x12+x10+x9+x6+x5+x4+x3+x2
x17+ x15
x17+ x14 + x12
x15+ x14 + x12
x15+ x12 + x10
x14 + x10
x14 + x11 + x9
x11+ x10 + x9
x11+ x8 + x6
x10+ x9 + x8 + x6
x10+ x7 + x5
x9+ x8 + x7 + x6+ x5
x9+ x6 + x4
x8 + x7 + x5+ x4
x8 + x5 + x3
x7 + x4+ x3
x7 + x4+ x2
x3+ x2
20

21. ОТА ИПКиС : Линейные рекуррентные последовательности

1.2. Остаточный многочлен (продолжение)
Следовательно: hД(x) = x3+ x2 (максимально возможная степень
многочлена равна 4).
Остаточный многочлен: h21(х) = x2+x.
Аналогичный результат может быть получен при выполнении
процедуры деления над коэффициентами при неизвестном:
21

22. ОТА ИПКиС : Определение параметров аддитивных скремблеров

1.2. Остаточный многочлен (продолжение)
100000000000000000000
100101
101000
100101
110100
100101
100010
100101
111000
100101
111010
100101
111110
100101
110110
100101
100110
100101
01100
│100101
22

23. ОТА ИПКиС : Линейные рекуррентные последовательности

1.2. Остаточный многочлен (продолжение)
hД(0,1) = ст01100
Остаточный многочлен: h21(0,1)= ст00110.
ЛРП МП, которая начинается с 21 элемента (пропущено 20 элементов)
выделена черным цветом:
1
21
{bi} ст0100101100111110001101110101000...
00110
│ {bi+20}
23

24. ОТА ИПКиС : Определение параметров аддитивных скремблеров

1.2. Алгоритм Гайбина
Алгоритм Гайбина позволяет существенно упростить процедуру
деления одночлена хk на f(х) при больших значениях k. Он основан на
очевидном тождестве (тождество Шёнемана) для многочленов над
полем GF(2):
f
2S
( x ) f ( x ).
2S
Алгоритм:
1. Допустим g(x)=xk.
2. Вычислить s = log2(deg[g(x)]/n) ,
где * - ближайшее меньшее целое,
deg[g(x)] - степень g(x).
3. Вычислить g(x): = g(x) mod fД(x 2 ).
4. Если step g(x) n, перейти к п.2.
5. Остаточный многочлен найден: hдв(x) = g(x).
S
24

25. ОТА ИПКиС : Определение параметров аддитивных скремблеров

1.2. Алгоритм Гайбина (продолжение)
Пример 2. Определить остаточной многочлен h21(х) для примера 1,
используя алгоритм Гайбина.
п.1. g(x) = х20
п.2. s = log
(20/5) = 2
S 2
п.3. fд( x 2 ) = x20+x8+1
x20
│x20+x8+1
x20+x8+1
1
x8+1
g(x) = x8+1
п.4. 8 > 5
25

26. ОТА ИПКиС : Линейные рекуррентные последовательности

1.2. Алгоритм Гайбина (продолжение)
п.2. s = log2 (8/5) = 0
2S
п.3. fД( x ) = x5+x2+1
x8+1
x8+x5+x3
x5+x3+1
x5+x2+1
x3+x2
g(x) = x3+x2
п.4. 3 < 5
п.5. hД(x) = x3+x2
h(x) = x2+х.
│x5+x2+1
x3+1
26

27. ОТА ИПКиС : Определение параметров аддитивных скремблеров

1. Идентификация аддитивного скремблера при полной априорной
неопределенности (продолжение)
Пример: Идентифицировать с помощью АПП-алгоритма аддитивный
скремблер по фрагменту цифрового потока:
{di} ст1110110010000100100011000010101010010000010
110110110101110110100000110111011101101000001101…
Известно:
- период следования детерминированных элементов в скремблируемом
ЦП – k = 3;
- известно значение детерминированного элемента – "0";
- степень характеристического многочлена n=5;
- pb = 0.
п.1. Демультиплексировать ЦП {di} на 3 подпотока:
1-ый подпоток {d3i+0} 10000001001...
2-ой подпоток {d3i+1} 11001100010...
3-ий подпоток {d3i+2} 11100010101...
27

28. ОТА ИПКиС : Определение параметров аддитивных скремблеров

1. Идентификация аддитивного скремблера при полной априорной
неопределенности (продолжение)
п.2. Построить 3 системы линейных двоичных алгебраических
уравнений:
1
0
0
0
0
0 0 0 0 c5 0
0 0 0 0 c4 0
0 0 0 0 c3 1
0 0 0 1 c 2 0
0 0 1 0 c1 0
1 1 0 0 1 c5 1
1 0 0 1 1 c 0
4
0 0 1 1 0 c3 0
0 1 1 0 0 c2 0
1 1 0 0 0 c1 1
1
1
1
0
0
1 1 0 0 c5 0
1 0 0 0 c4 1
0 0 0 1 c3 0
0 0 1 0 c2 1
0 1 0 1 c1 0
п.3. Решить системы линейных двоичных алгебраических уравнений:
1 0
0 1
0 0
0 0
0 0
характеристический многочлен f(х) = х5+х3+х2+х+1
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
1
0
0
0
0
0
1
0
1
0
0
0
0
0
1
0
0
0
0
0
1
0
0
0
1
1
0
0
0
0
0
1
0
0
0
0
0
1
0
0
1
0
0
0
0
0
1
0
0
0
0
0
1
1
0
1
1
1
28

29. ОТА ИПКиС : Определение параметров аддитивных скремблеров

1. Идентификация аддитивного скремблера при полной априорной
неопределенности (продолжение)
п.5. Проверка на достоверность 3-его подпотока; Если
нет СТОП.
п.7. Вычислить обратный коэффициент выборки k
Построим таблицу:
k = 21.
п.8. Построить ЛРП МП с характеристическим многочленом
f3(x)=х5+х3+х2+х+1 и начальной фазой: 11100
{b3i} 11100010101 1010000110 010011111011100...
29

30. ОТА ИПКиС : Определение параметров аддитивных скремблеров

1. Идентификация аддитивного скремблера при полной априорной
неопределенности (продолжение)
п.9. Выбрать из полученной последовательности
10 элементов, начиная с
первого, с коэффициентом выборки k = 21 (элементы: 0, 21, 11(42), 1(63)
…).
В результате получим 10 элементов ЛРП МП скремблера {bi}:
1011101010 ... .
п.10. Построить систему линейных двоичных алгебраических
уравнений:
1
0
1
1
1
0 1 1 1 c5 0
1 1 1 0 c4 1
1 1 0 1 c3 0
1 0 1 0 c2 1
0 1 0 1 c1 0
30

31. ОТА ИПКиС : Определение параметров аддитивных скремблеров

1. Идентификация аддитивного скремблера при полной априорной
неопределенности (продолжение)
п.11. Решить систему линейных двоичных алгебраических уравнений:
1
0
0
0
0
0
1
0
0
0
0
0
1
0
0
0
0
0
1
0
0
0
0
0
1
1
0
1
0
0
Следовательно, (c1 … c5) = (00101)
п.12. Аддитивный скремблер идентифицирован:
- характеристический многочлен f(x) = x5+x3+1;
- начальная фаза b1...b5 10111.
Кроме того, определена позиция j=2 первого детерминированного
элемента, с которого можно проводить дескремблирование ЦП {bi+2} с
полученной начальной фазой.
31

32. ОТА ИПКиС : Определение параметров аддитивных скремблеров

1. Идентификация аддитивного скремблера при полной априорной
неопределенности (продолжение)
Примечание к примеру:
Если необходимо дескремблировать ЦП {di}, начиная с первого
элемента, тогда следует:
1) сгенерировать j элемент bj-1bj-2… b0, задав в качестве
характеристического многочлена многочлен, двойственный
характеристическому многочлену скремблера, fдв(x) и начальную фазу –
(стbnbn-1...b1).
2) дескремблировать ЦП {di} с характеристическим многочленом f(x) и
начальной фазой (стb0b1...bn-1).
32

33. ОТА ИПКиС : Определение параметров аддитивных скремблеров

1. Идентификация аддитивного скремблера при частичной
(доразведка) априорной неопределенности
Идентификация аддитивного скремблера при частичной априорной
неопределенности (доразведка) c помощью статистических подходов не
применяется в связи с высокой вычислительной сложностью.
33