Числовые характеристики ДСВ

1. Числовые характеристики ДСВ

Пример Партия в шашки
X
P
0
0,2
1
0,3
2
0,5
n
M X xi pi
i 1
M X 0 0,2 1 0,3 2 0,5 1,3
D X m 2 X
р
mX
m2 M X
2
2
mx
D X 2,3 1,3 2,3 1,69 0,61
2
х
2
2
2
0 0 ,2 1 0 ,3 2 0 ,5 2 ,3
σ X D X
σ X 0,61 0,78
m 100%
v X
v X 0,78 1,3 100% 60%
1

2. Закон распределения ДСВ

Способы задания ЗР ДСВ
1) таблица распределения
2) общая формула
3) функция распределения
4) производящая функция
4
Производящая функция – форма закона
распределения ДСВ
ДСВ Х задана формулой
z
Р X k pk
pk z
k 0
k
k 0, 1, 2, ...
, 0 z 1
2

3. Производящая функция

k
z pk z , 0 z
k 0
1
Свойства
1. z , z ,...
ряды сходятся абсолютно
2. 1 1
3. 1 m x
4. 1 1 m 2 X
1 pk 1
z pk k z k 1
1 pk k m x
k 2
z pk k k 1 z
2
1 pk k pk k m 2 mx
3

4. Производящая функция

z
pk
z , 0 z 1
k
k 0
1. z , z ,...
2. 1 1
Свойства
3. 1 m x
4. 1 1 m 2 X
ряды сходятся абсолютно
M X 1
D X 1 1 1
2
4

5. Производящая функция

Пример Партия в шашки M X 1,3 D X 0,61
X
0
1
2
k
z pk z , 0 z 1
P 0,2 0,3 0,5
k 0
z 0,2 z 0,3 z 0,5 z 0,2 0,3 z 0,5 z
z 1
z 0,3 0,5 2 z 0,3 z
0
1
2
2
M X 1 M X 0,3 1 1,3
m 2 1 1 m 2 1 1,3 2,3
D X m 2 X
2
mx
D X 2,3 1,3 0,61
2
5

6. Распределение Бернулли Ber (p)

Проводится одно испытание, в результате которого
может наступить (не наступить) событие А.
С.в. Х – индикатор события А.
n
X
P
0
1-р
1
р
D X m 2 X
2
mx
M X xi pi
i 1
M X 0 1 p 1 p p
D X p p pq
2 2
2
m M X 0 1 p 1 p p
2
2
M X p
D X pq
6

7. Биномиальное распределение Bin (n, p)

Х – количество успешных испытаний в схеме из n
испытаний Бернулли:
1) проводится n независимых опытов;
2) в каждом опыте ровно два исхода: У и Н;
3) Р(Уi ) = р, Р(Нi ) = q, р + q = 1
Р Х k
k k n k
Cn p q ,
z pz q
*
np q k np p
n
k 0,n
m np
D npq
7

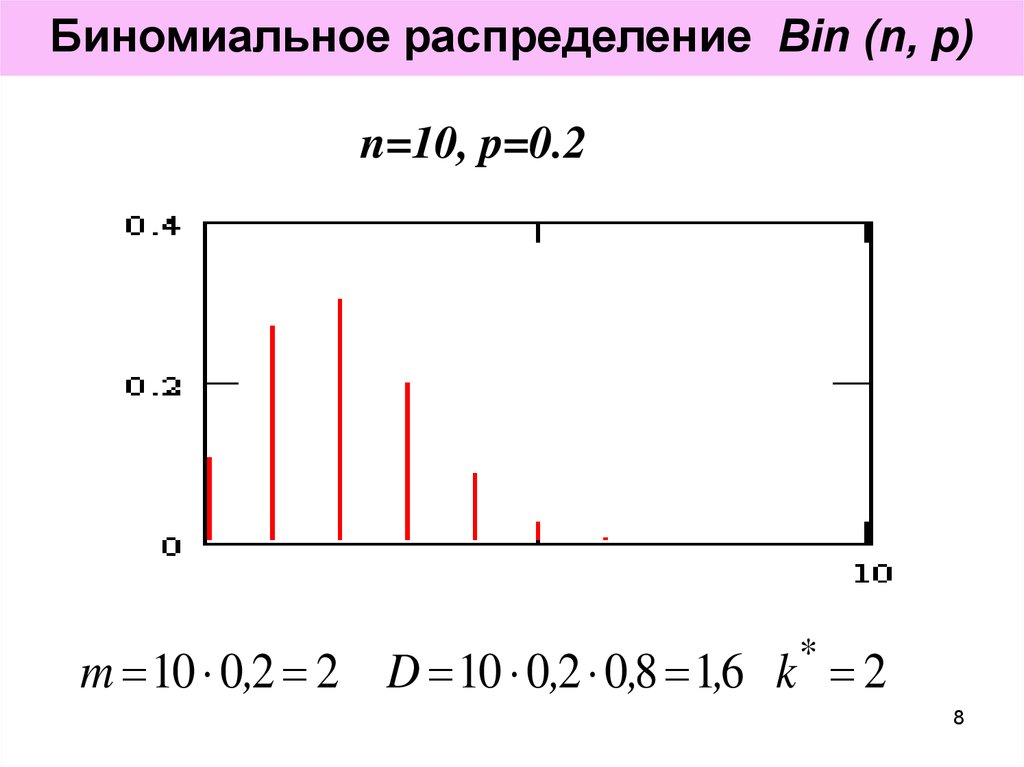
8. Биномиальное распределение Bin (n, p)

n=10, p=0.2
m 10 0,2 2 D 10 0,2 0,8 1,6 k 2
*
8

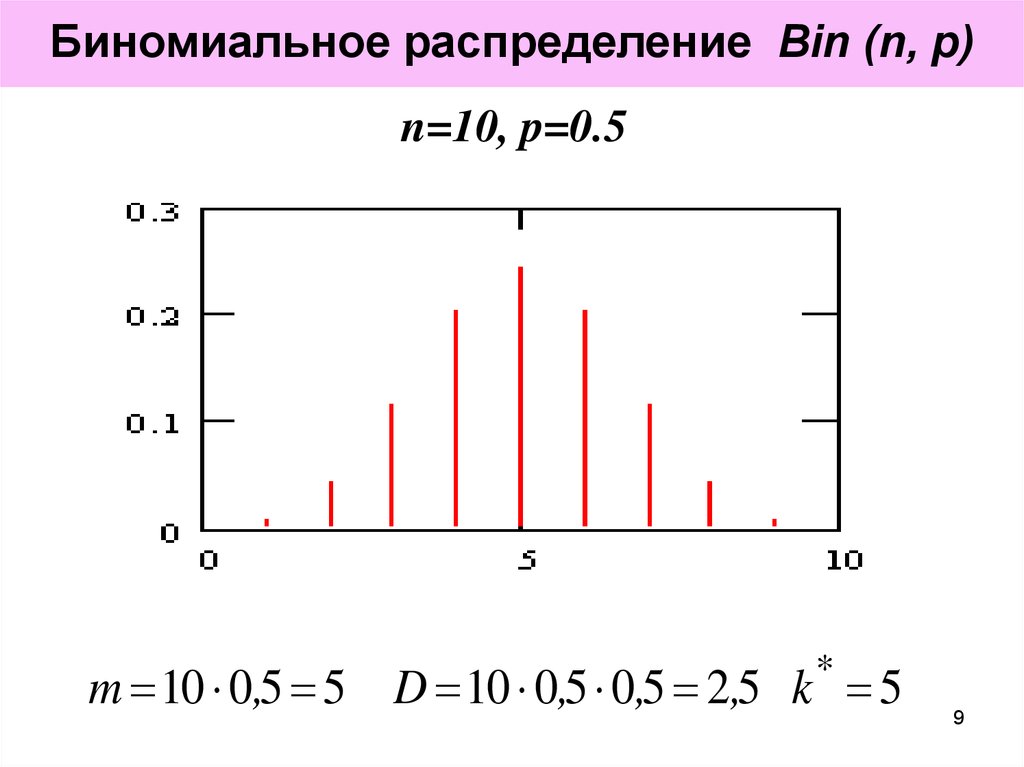
9.

Биномиальное распределение Bin (n, p)
n=10, p=0.5
m 10 0,5 5 D 10 0,5 0,5 2,5 k 5
*
9

10.

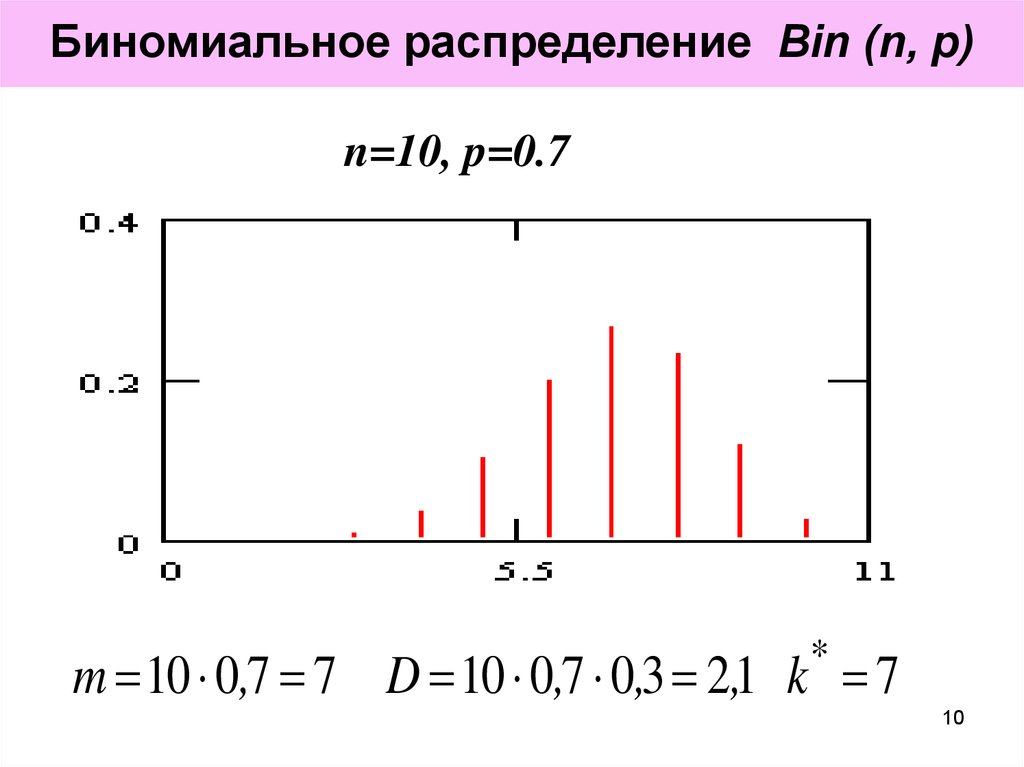
Биномиальное распределение Bin (n, p)
n=10, p=0.7
m 10 0,7 7 D 10 0,7 0,3 2,1 k 7
*
10

11.

Биномиальное распределение Bin (n, p)
n=11, p=0. 5
m 11 0,5 5,5 D 11 0,5 0,5 2,75
*
*
k 1 5 k 2 6
11

12. Геометрическое распределение G(р)

Х – количество опытов (неудач) до первого успеха
1) опыты независимы;
2) в каждом опыте ровно два исхода: У и Н;
3) Р(Уi ) = р, Р(Нi ) = q, р + q=1
k
P X k pq ,
p
z
1 qz
k 0,1,2,....
q
m
p
D
Y – количество опытов до первого успеха,
включая успешный;
Y=X+1
q
p
2
12

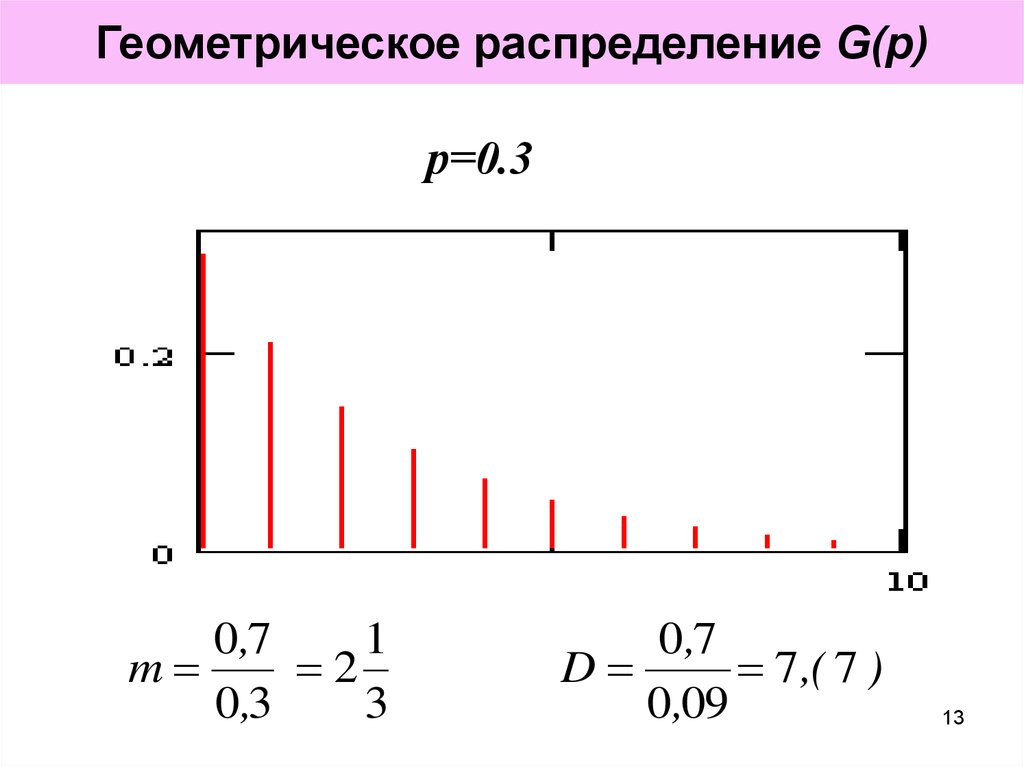
13. р=0.3

Геометрическое распределение G(р)
р=0.3
0 ,7
1
m
2
0 ,3
3
0,7
D
7 ,( 7 )
0 ,09
13

14. Распределение Пуассона П(a)

Х – количество событий, происходящих
с интенсивностью а в единицу времени
k
a a
P X k e ,
k!
z e
a z 1
k 0,1,2,...
m a
D a
Х – предельное для биномиального
распределения при условии np a
n
14

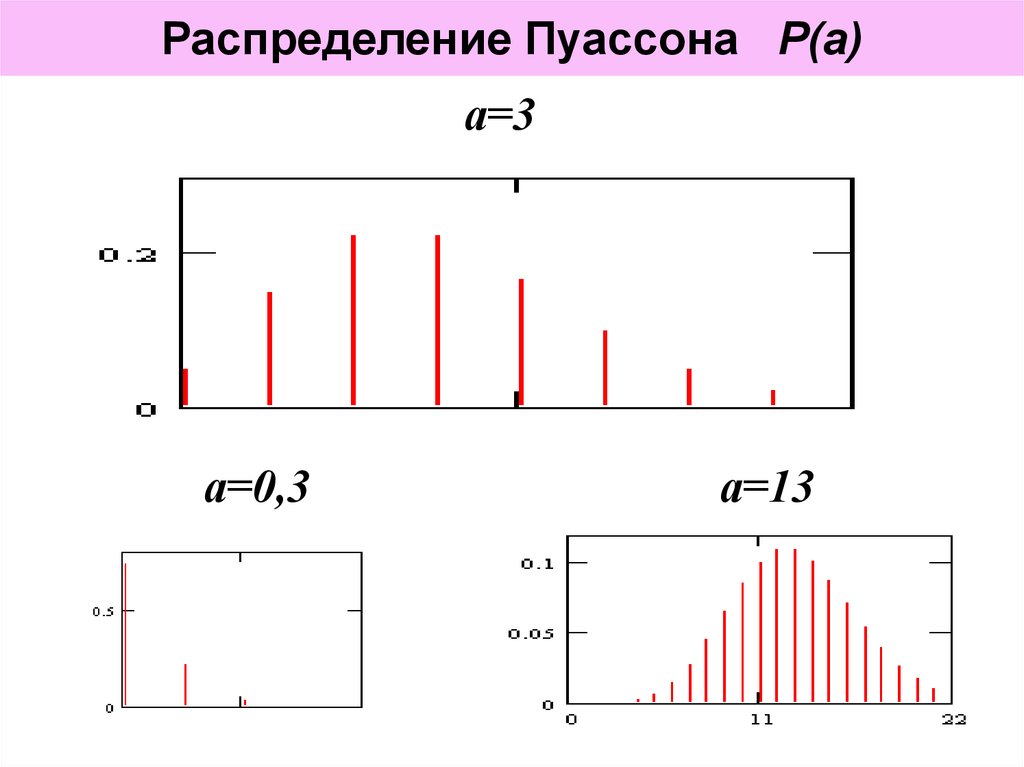
15. а=3

Распределение Пуассона Р(а)
а=3
а=0,3
а=13
15