Similar presentations:
Выборки. Комбинаторные схемы
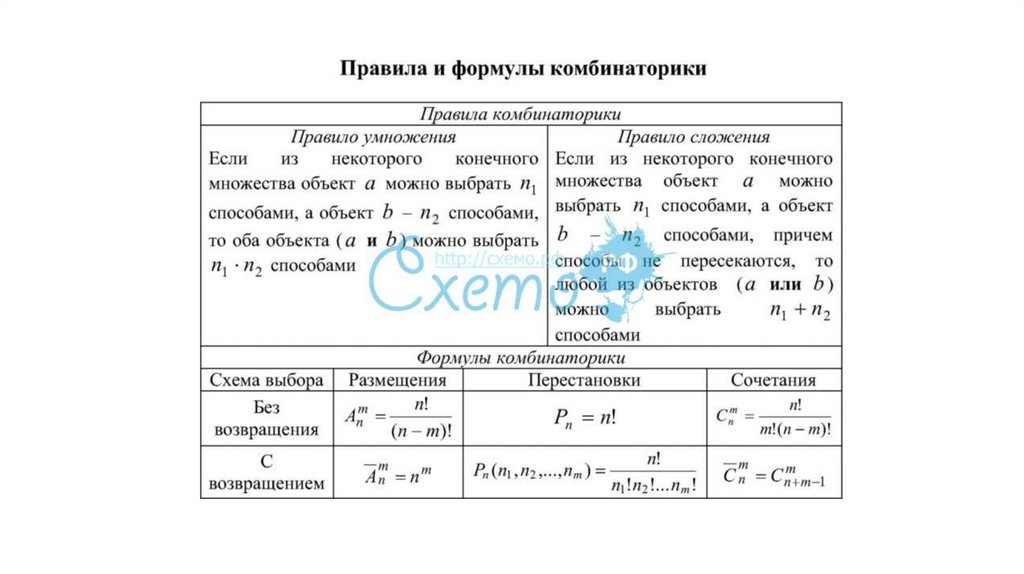
1. ВЫБОРКИ
2. Комбинаторные схемы: - Выбор элементов из конечного множества и размещение их в выборке - Раскладка предметов по ящикам
3.
Полный переборПеречисляющие
функции
Комбинаторные
числа
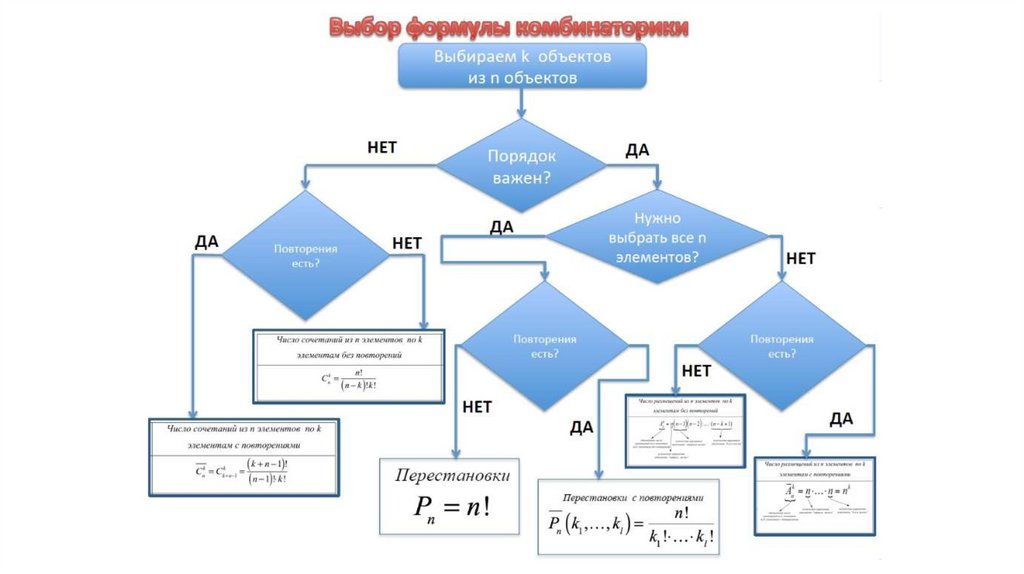
4. Способы задания комбинаторных чисел
Замкнутый видРекуррентные соотношения
Метод производящих функций
Асимптотические оценки
5.
6.
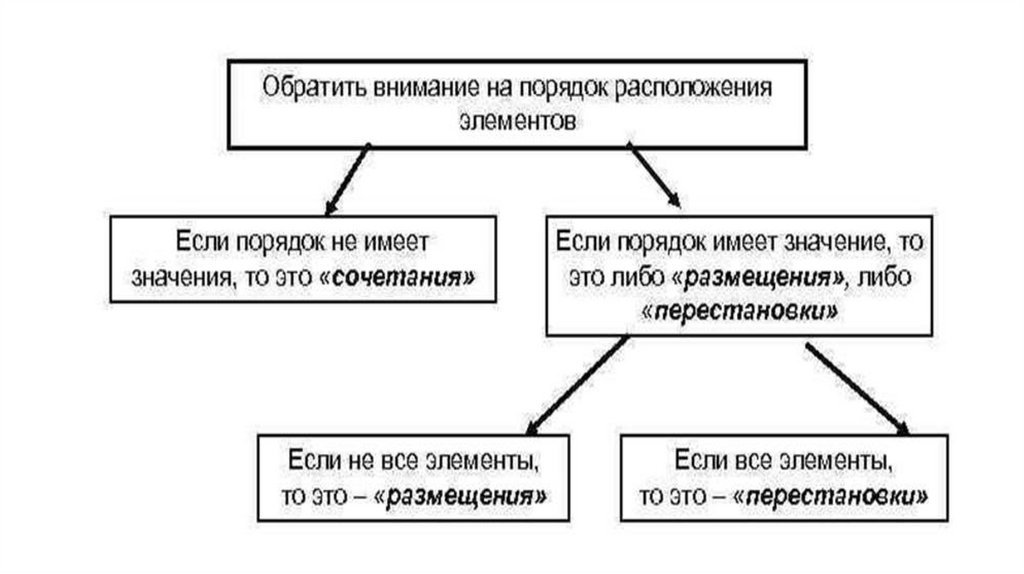
7. S={a, b, c} n=3 k=2 сочетания без повт.: ab, ac, bc размещения без повт.: ab, ba, ac, ca, bc, cb сочетания с повт.: ab, ac, bc,
aa, bb, ccразмещения с повт.: ab, ba, ac, ca, bc, cb, aa, bb, cc
перестановки всех эл-тов: abc, acb, bac, bca, cab, cba
8.
.Размещения без повторений
Определение. Пусть имеется множество, состоящее из n
элементов. Упорядоченный набор из k различных элементов
этого множества называется размещением без повторений
(или просто размещением) из n элементов по k.
Число размещений из n элементов по k обозначают
k
An
9.
10.
Пример 1. Студенческая группа состоитиз 25 человек. Нужно выбрать старосту,
заместителя
старосты
и
профорга.
Сколькими способами это можно сделать,
если каждый студент может занимать только
одну должность.
Пример 2. Сколькими способами можно
переставить буквы слова «комбинация» так,
чтобы не менялся порядок гласных букв?
11.
Перестановки без повторенийОпределение. Пусть имеется множество, состоящее из n элементов.
Упорядоченная последовательность всех элементов этого множества
называется перестановкой без повторений (или просто перестановкой).
Замечание. Перестановка без повторений — это размещение без
повторений из n элементов по n.
Число перестановок без повторений из n элементов обозначают
Pn
12.
13.
Пример 3. Для дежурства на факультете спонедельника по субботу выделено 6 студентов
из группы. Староста группы должен составить
график дежурства. Сколькими способами он
может это сделать?
Пример 4. Сколькими способами можно
расставить 8 ладей, чтобы они не били друг
друга.
14.
Сочетания без повторенийОпределение. Пусть имеется множество, состоящее из n
элементов. Подмножество из k элементов этого множества
называется сочетанием без повторений (или просто
сочетанием) из n элементов по k.
15.
16.
Пример 5. Студенческая группа состоит из 25 человек.Нужно выбрать 3 делегатов на профсоюзную конференцию.
Сколькими способами это можно сделать?
Пример 6. Сколькими способами можно поставить на
шахматную доску 8 ладей.
Пример 7. Трое ребят собрали 40 яблок. Сколькими
способами они могут их разделить, если все яблоки
считаются одинаковыми?
Пример 8. Из лаборатории, в которой работают 20
человек, 5 сотрудников должны уехать в командировку.
Сколько может быть различных составов этой группы, если
начальник лаборатории, его заместитель и главный инженер
одновременно уезжать не должны?
Пример 9. Имеются m белых и n черных шаров, m > n.
Сколькими способами можно все шары разложить в ряд
так, чтобы никакие два черных шара не лежали рядом?
Пример 10. Сколькими способами можно переставлять
буквы слова «Абакан» так, чтобы согласные шли в
алфавитном порядке? Решить задачу при дополнительном
условии, что буквы «а» не идут подряд.
17.
18.
.Размещения с повторениями
Определение. Пусть дано множество, состоящее из n элементов.
Упорядоченный набор из k элементов этого множества, среди которых могут
быть одинаковые, называется размещением с повторениями из n элементов
по k.
Число размещений с повторениями из n элементов по k обозначают
A
k
n
19.
kn
A n
k
20.
Пример1.
Чемодан
имеет
цифровой замок, состоящий из
6
дисков.
Сколько
различных
комбинаций
может
быть
зашифровано?
Пример 2. Сколько существует
подмножеств
у
множества
A
мощности n, т.е. чему равно |P(A)|?
21.
Перестановки с повторениямиОпределение. Пусть дано множество, состоящее из k элементов.
Упорядоченный набор из n элементов этого множества такой, что 1-й
элемент взят n1 раз, 2-й элемент — n2 раз, …, k-й элемент — nk раз,
называется перестановкой с повторениями.
Замечание. Очевидно, что n1 + n2 + … + nk = n.
Число перестановок с повторениями из n элементов обозначают
P(n1, n2, …, nk).
22. Выпишите все перестановки букв в словах: МИР, ДЕД, ПАРК, ПАПА
23.
( n1 n2 ... nk ) !n!
P( n1 , n2 ,..., nk )
n1! n2! ... nk !
n1! n2! ... nk !
24.
Пример 3. Сколькими способамиможно расставить белые шахматные
фигуры (2 коня, 2 слона, 2 ладьи,
ферзь и король) на первой линии
шахматной доски?
Пример 4. Садовник должен в
течение 3 дней посадить 10 деревьев.
Сколькими способами он может
распределить по дням работу, если
будет сажать не менее 1 дерева в день?
25.
.Сочетания с повторениями
Определение. Пусть дано множество, состоящее из n элементов.
Неупорядоченный набор из k элементов этого множества, среди
которых могут быть одинаковые, называется сочетанием с
повторениями из n элементов по k.
Число сочетаний с повторениями из n элементов по k обозначают
k
Cn
26.
Пример 5. В буфете продается 4 видапирожных. Сколькими способами можно
купить 7 пирожных?
7
C4
1101110101
27.
28.
29.
30.
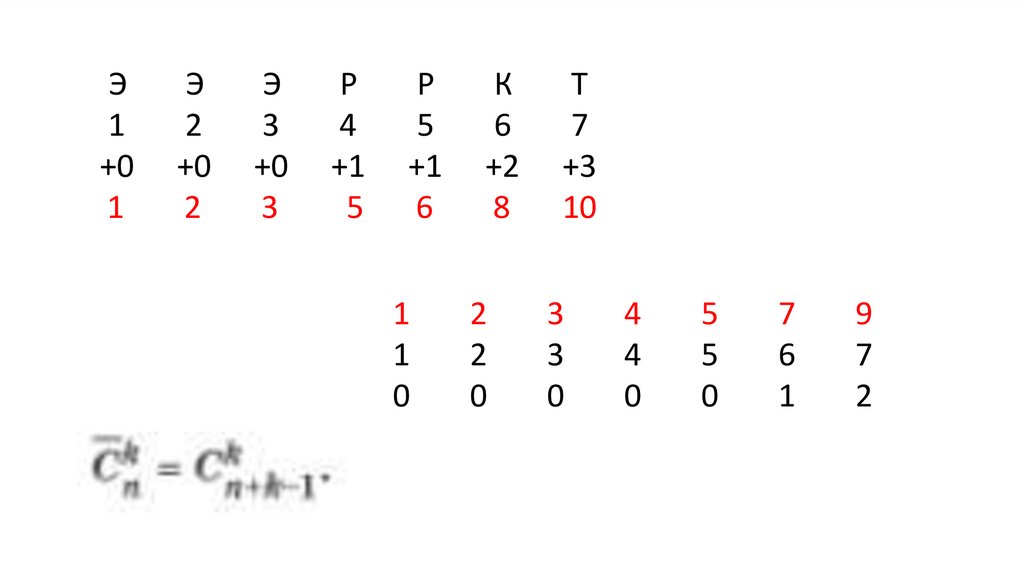
Э1
+0
1
Э
2
+0
2
Э
3
+0
3
Р
4
+1
5
Р
5
+1
6
К
6
+2
8
Т
7
+3
10
1
1
0
2
2
0
3
3
0
4
4
0
5
5
0
7
6
1
9
7
2
31.
32.
Пример 11. Из 10 красных роз и 8 белых рознужно составить букет, содержащий 2 красные
розы и 3 белые. Сколько можно составить
различных букетов?
33.
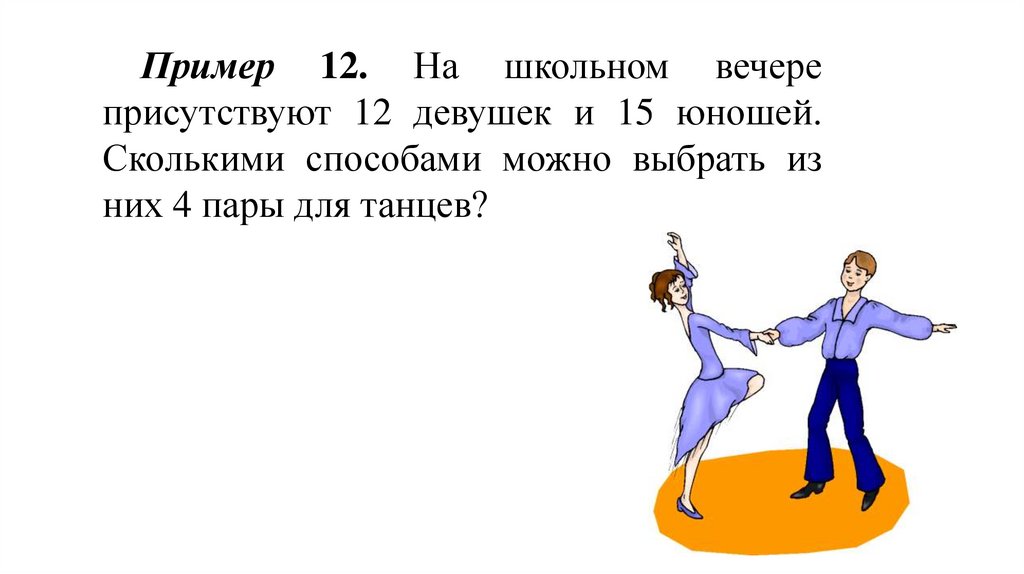
Пример 12. На школьном вечереприсутствуют 12 девушек и 15 юношей.
Сколькими способами можно выбрать из
них 4 пары для танцев?
34.
Пример 13. Сколькими способами можнопереставить буквы слова «ЛОГАРИФМ» так,
чтобы второе, четвертое и шестое места были
заняты согласными буквами?
35.
Пример 14. Сколькими способами можнопереставить буквы слова «ПАСТУХ» так, чтобы
между двумя гласными были две согласные
буквы?
36.
Пример 15. Сколькими способами можнорассадить за 15 парт 15 мальчиков и 15 девочек так,
чтобы за каждой партой слева сидел мальчик, а
справа – девочка?
37.
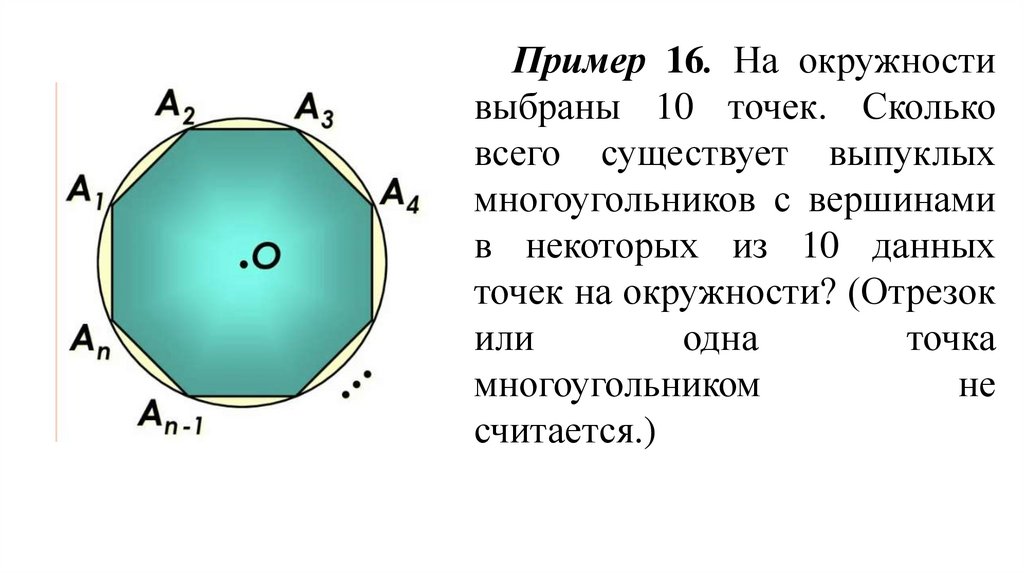
Пример 16. На окружностивыбраны 10 точек. Сколько
всего существует выпуклых
многоугольников с вершинами
в некоторых из 10 данных
точек на окружности? (Отрезок
или
одна
точка
многоугольником
не
считается.)
38.
Пример 17. На каждом борту лодки сидят по 4 человека. Сколькимиспособами можно выбрать команду для этой лодки, если есть 31
кандидат, причем 10 человек хотят сидеть на левом борту лодки, 12 —
на правом, а для 9 человек безразлично где сидеть?
39.
Пример 18. Восемь человек водят хоровод.Сколькими способами они могут стать в круг?
40.
Пример 19. 9 из 10 карт, среди которых есть червовый туз,раздаются трем лицам так, что первый получает 3, второй 4, а
третий 2. Сколько существует способов раздачи, при которых
червовый туз попадает к третьему лицу?
41.
Пример 20. Из колоды, содержащей 52карты, вынули 10 карт. Во скольких случаях
среди этих карт окажется:
1) хотя бы один туз;
2) один туз;
3) не менее двух тузов;
4) два туза?
42.
Пример 21.Сколькими способами
можно разделить колоду
из 36 карт пополам так,
чтобы в каждой пачке
было по два туза?
43.
Пример 22. На заседании научного студенческогообщества присутствуют 52 студента: по 13
студентов от четырех факультетов. Сколькими
способами можно избрать правление общества в
составе 4 лиц так, чтобы в состав правления вошли
представители: 1) ровно трех факультетов; 2) хотя
бы трех факультетов?
44.
Пример 23. Сколькими способами можновыбрать из одной колоды карт, содержащей 52
карты, 6 карт так, чтобы среди них были все четыре
масти?
45.
Пример 24. Имеется n абонентовтелефонной
сети.
Сколькими
способами
можно
одновременно
соединить три пары?
46.
Пример 6. Сколькими способами можнопереставить
буквы
слова
«обороноспособность» так, чтобы две
буквы «о» не шли подряд?
47.
Пример 7. Сколькимиспособами
можно
разложить 3 монеты по
рублю и 10 полтинников
в 4 различных пакета?
48.
Пример 8. Сколько четырехзначных чиселможно составить из цифр числа 123 153?





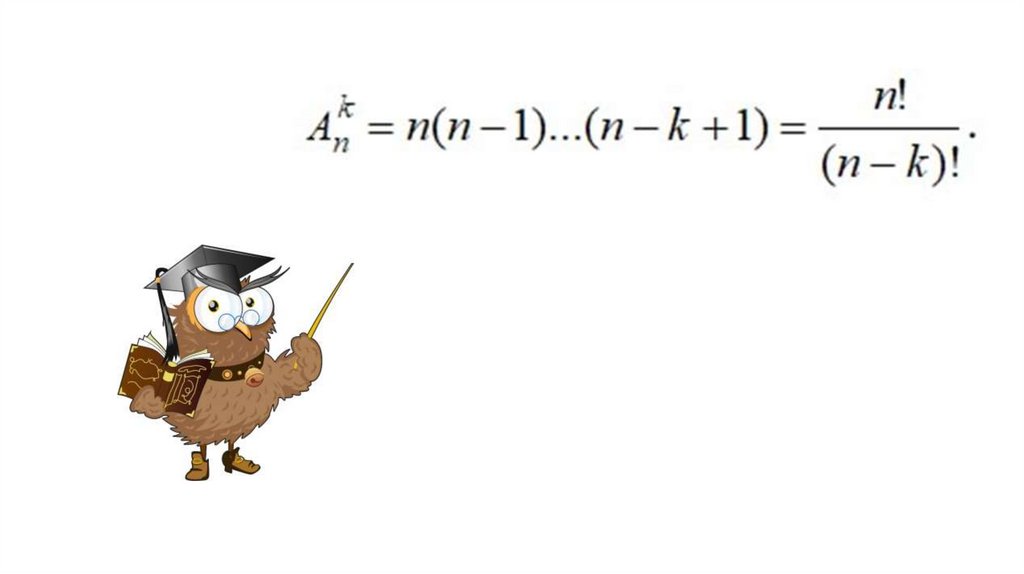


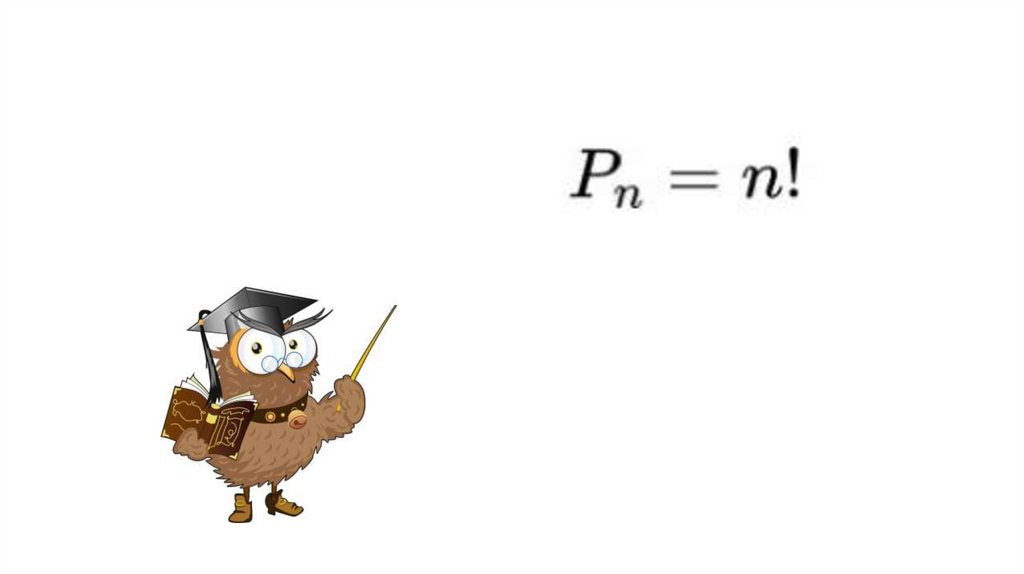






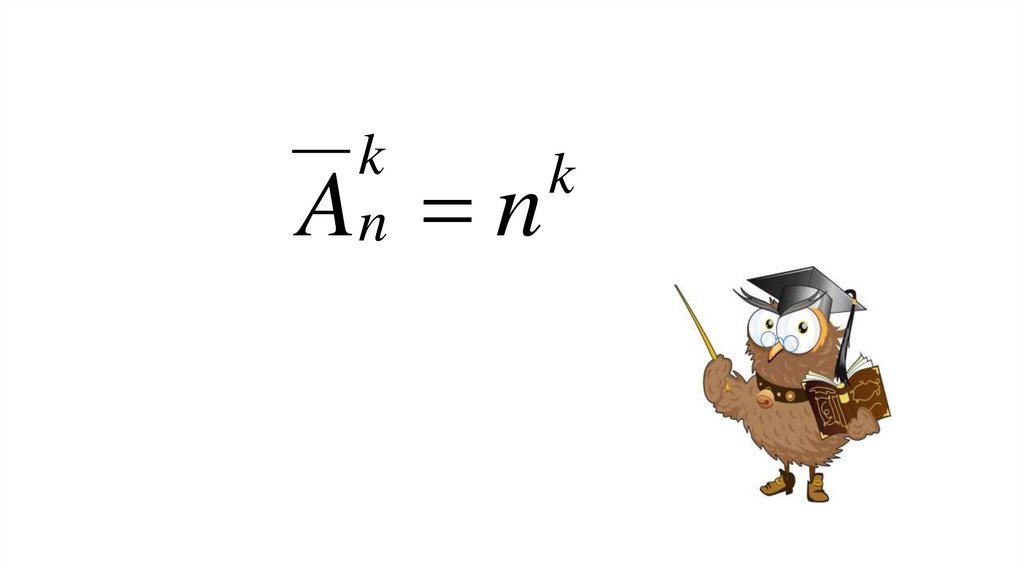



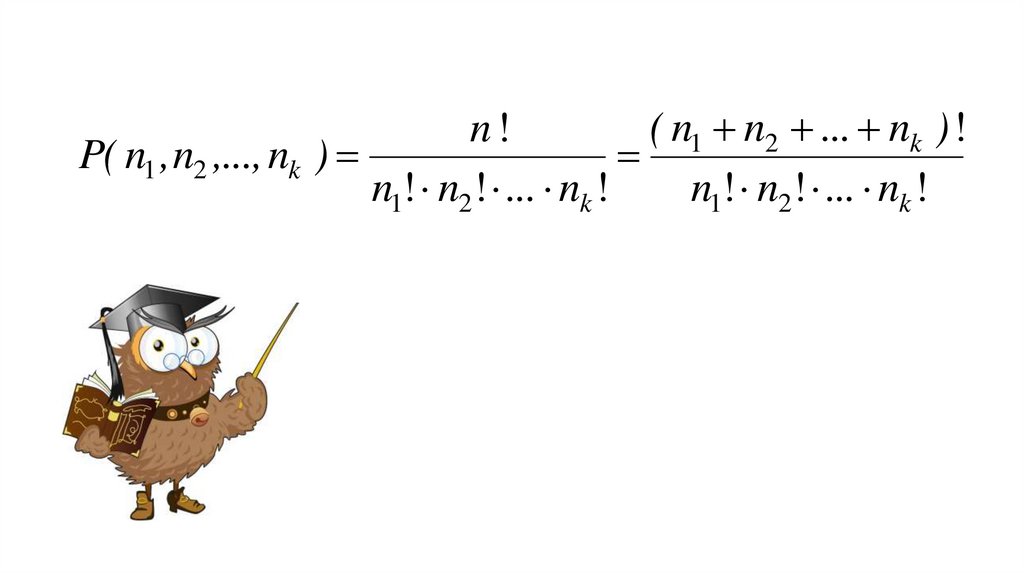




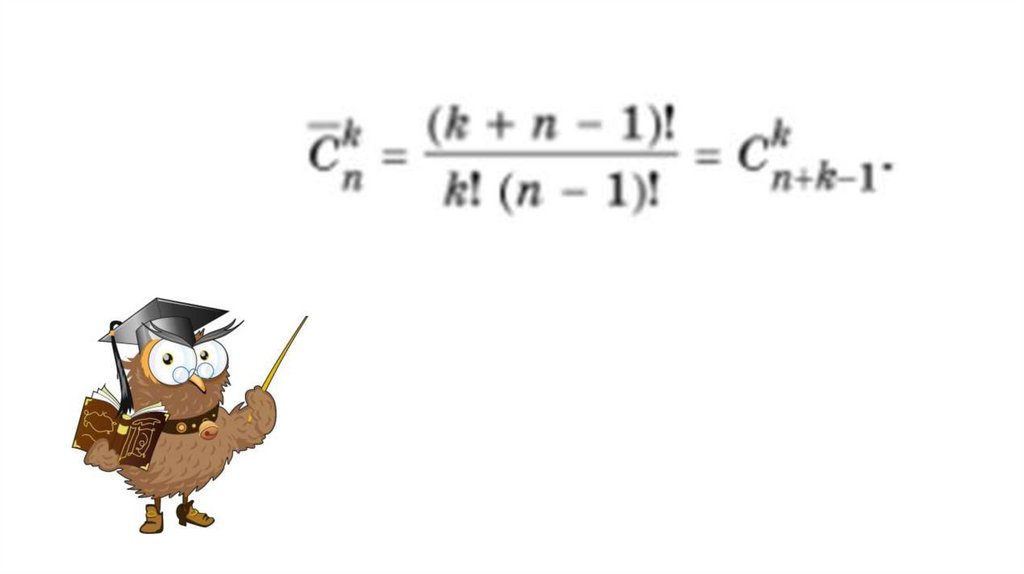
















 mathematics
mathematics








