Неклассические логики

1. НЕКЛАССИЧЕСКИЕ ЛОГИКИ

Саровский физико-технический институт
Национального исследовательского ядерного университета МИФИ
НЕКЛАССИЧЕСКИЕ ЛОГИКИ
Алексеев В.В.
Саров
2016
1

2. 1. Трехзначные логики

Трехзначная логика Лукасевича.
1. Высказывание, которое может принимать
одно из трех значений: 1, ½, 0.
2. Введены операции:
- отрицание, обозначаемое Nx;
- конъюнкция (Кху);
- дизъюнкция (Аху);
- импликация (Сху).
2

3.

Эти операции определены следующим
образом:
• Nx=1-x;
• Kxy=min(x, у);
• Аху=тах(х, у);
• Cxy=min(1, 1-х+у), т.е.: Сху=1, если х<у;
Сху=1-х+у, если х>у.
3

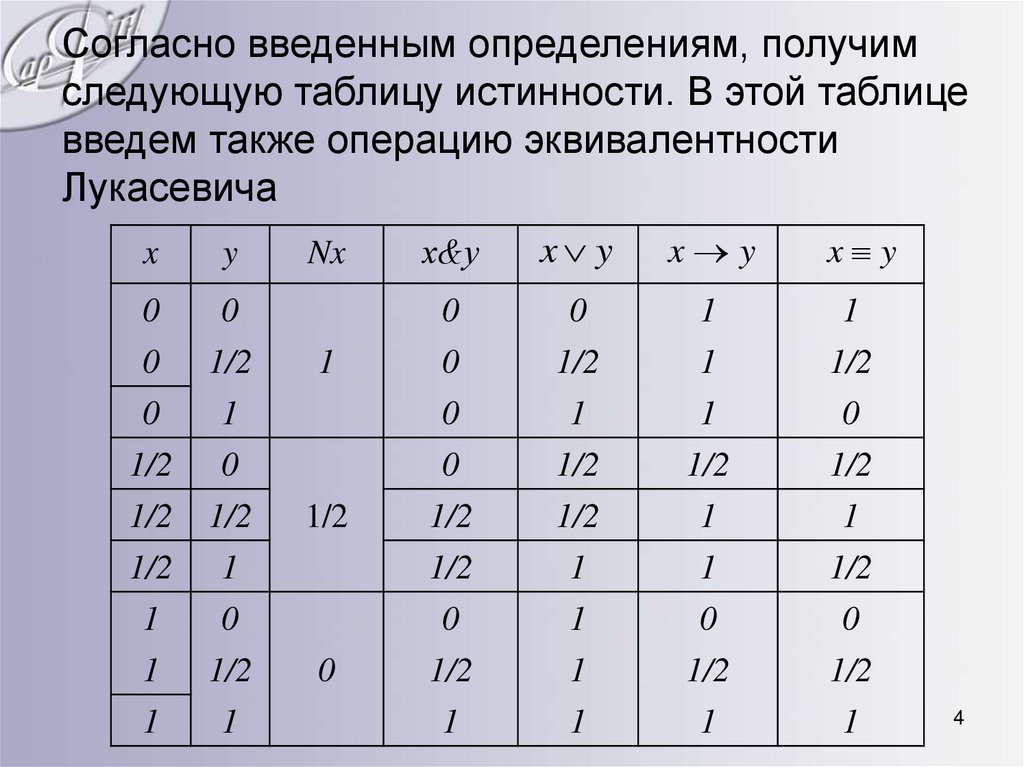
4.

Согласно введенным определениям, получим
следующую таблицу истинности. В этой таблице
введем также операцию эквивалентности
Лукасевича
x
y
0
0
0
1/2
0
1/2
1/2
1
0
1/2
1/2
1
1
1
0
1/2
1
1
Nx
х&у
x y
x y
x y
1
0
0
0
1/2
1
1
1
1/2
1/2
0
0
1/2
1
1/2
1/2
1
1/2
1
0
1/2
1
0
1/2
0
1/2
1
1
1
1
0
1/2
1/2
0
1/2
1
1
1
1
4

5.

Рассмотрим, например выражение N(x&y). Легко
видеть, что N(x&y)=1-min (х,у)=max(1-x, 1y)=(Nx) (Ny). Аналогичным образом можно
получить, что N(x y)=(Nx)&(Ny).
Следовательно,
в этой логике выполняются
законы де Моргана.
Имеются и другие сходства с двузначной
логикой, но есть и различия, например, не
выполняется закон исключённого третьего,
т.е. x (Nx) не всегда истинно; есть и другие
различия.
5

6. Трёхзначная логика Гейтинга.

• В двузначной логике являются
тавтологиями как x x , так и x x .
• Из предположения, что тавтологией
можно считать только формулу x x
Гейтинг разработал новую трёхзначную
логику.
• Пусть имеем вновь множество
высказываний, каждое из которых
принимает одно из значений: 1, 1/2 и 0.
• Операции Гейтинга вводятся согласно
6
следующей таблице

7.

x
0
y
0
Nx
0 1/2
0
1
1/2 0
1/2 1/2
1/2 1
1
0
1 1/2
1
1
1
1/2
0
x y
х&у
0
x y x y
0
1
1
0
0
0
1/2
1/2
0
1/2
1
1/2
1
1/2
1/2
1
1
1
1
1
1
0
1
1
0
1/2
1
0
0
0
1
1/2
0
1/2
1
7

8.

• Из таблицы видно, что конъюнкция и
дизъюнкция определены следующим
образом:
x & y min( x , y );
x y max( x , y ) ;
а импликация по формуле:
x y 1, если x y ;
x y y , если x y .
В этой логике, как и в логике Лукасевича, если оставить
только значения 0 и 1 (исключить третье значение 8
значение ½), то получим обычную двузначную логику

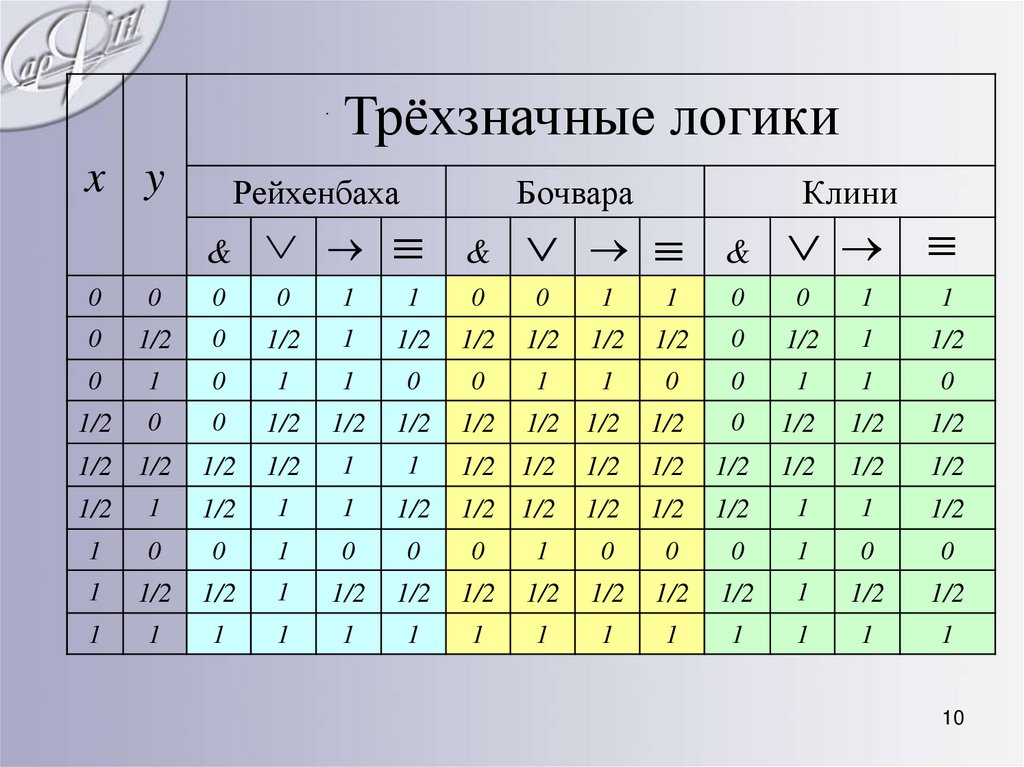
9. Трёхзначные логики Рейхенбаха, Бочвара и Клини

• Наиболее известными являются пять
трёхзначных логик. К ним относятся
указанные логики Лукасевича и Гейтинга, а
также трёхзначные логики Рейхенбаха,
Бочвара и Клини.
• В каждой из этих логик есть отрицание,
такое, что x 1 x.
• Значения для конъюнкции, дизъюнкции,
импликации и эквивалентности
высказываний определяется по следующей
таблице:
9

10.

Трёхзначные логики
x y
Рейхенбаха
Бочвара
Клини
&
&
&
0
0
0
0
1
1
0
0
1
1
0
0
1
1
0
1/2
0
1/2
1
1/2
1/2
1/2
1/2
1/2
0
1/2
1
1/2
0
1
0
1
1
0
0
1
1
0
0
1
1
0
1/2
0
0
1/2
1/2
1/2
1/2
1/2 1/2
1/2
0
1/2
1/2
1/2
1/2 1/2
1/2
1/2
1
1
1/2 1/2
1/2
1/2
1/2
1/2
1/2
1/2
1/2
1
1/2
1
1
1/2
1/2 1/2
1/2
1/2
1/2
1
1
1/2
1
0
0
1
0
0
0
1
0
0
0
1
0
0
1
1/2
1/2
1
1/2
1/2
1/2
1/2
1/2
1/2
1/2
1
1/2
1/2
1
1
1
1
1
1
1
1
1
1
1
1
1
1
10

11.

Из определений операций видно:
• во всех этих пяти логиках значения
операций совпадают с их значениями
для классической двузначной логики,
когда аргументы х и у принимают
значения из {0, 1}.
• различаются когда значение хотя бы
одного из аргументов х, у принимают
значение 1/2 .
11

12.

В логике Рейхенбаха введены три
отрицания:
• циклическое отрицание, обозначаемое
«~А»;
• диаметральное отрицание, обозначаемое
через « A»;
• полное отрицание, обозначаемое через «А».
12

13. Эти операции вводятся по следующей таблице:

А
~А
A
-А
1
1/2
0
1/2
0
1
0
1/2
1
1/2
1
1
13

14. 2. Многозначные логики

• Конечнозначная (k-значная, k>2)
логика Поста является обобщением
двузначной логики, т.е. при к=2
получится двузначная логика.
Рассмотрим множество высказываний
(переменных), каждое из которых может
принимать одно из значений 0,1,2, ...,к-1.
14

15. На множестве введённых к - значных высказываний вводятся операции:

k 1, если x m,
Im( x )
0, если x m.
Функция Iт(х) называется характеристической
функцией и обозначается иногда как хт .
15

16.

x y max( x , y )
k 1, если 0 x y k - 1,
x y
(k - 1) - x y, если 0 y x k - 1.
16

17. Используя введённые операции можно строить суперпозиции этих функций, исследовать их свойства. Также можно вводить нормальные

формы, доказать
следующее соотношение:
f ( x1 , x2 xn )
( a1 ,a2 an )
I a1 & I a2 & I an & f ( a1 ,a2 , an ),
где дизъюнкция берётся по всевозможным
наборам значений ( a1 ,a2 , an ) переменных
( x1 , x2 , xn )
17

18. Теорема Число различных функций k-значной логики, зависящих от n переменных равно

K1 , K 2 , K r( k )
Теорема Число различных функций kзначной логики, зависящих от n
kn
переменных равно k .
Система функций k-значной логики 1 , 2 , m
называется функционально полной, если
любую функцию f k-значной логики можно
выразить через функции из 1 , 2 , m .
Существует и критерий полноты системы
функций.
18

19.

Теорема (о функциональной полноте,
теорема А. В. Кузнецова). Для каждой kзначной логики существует конечное число
замкнутых классов K1 , K 2 , K r( k ) таких, что
для полноты системы функций k-значной
логики 1 , 2 , m необходимо и достаточно
чтобы не содержалась целиком ни в одном
из классов K1 , K2 , K r( k )
19

20. Многозначная логика Лукасевича

• В отличие от k-значной логики Поста в
k-значной логике Лукасевича считается,
что истинностные значения переменных
образуют следующее множество:
0
1
2
k 2 k 1
Tk 0
,
,
,
,
1 .
k 1 k 1 k 1
k 1 k 1
Эти истинностные значения можно
интерпретировать как степень (уровень)
истинности.
20

21. Операции определяются следующим образом:

Nx 1 x ;
x & y min( x , y );
x y max( x , y );
x y min(1,1 y x );
x y 1 | x y | .
21