Реология полимеров и наполненных систем

1. Реология полимеров и наполненных систем

1

2.

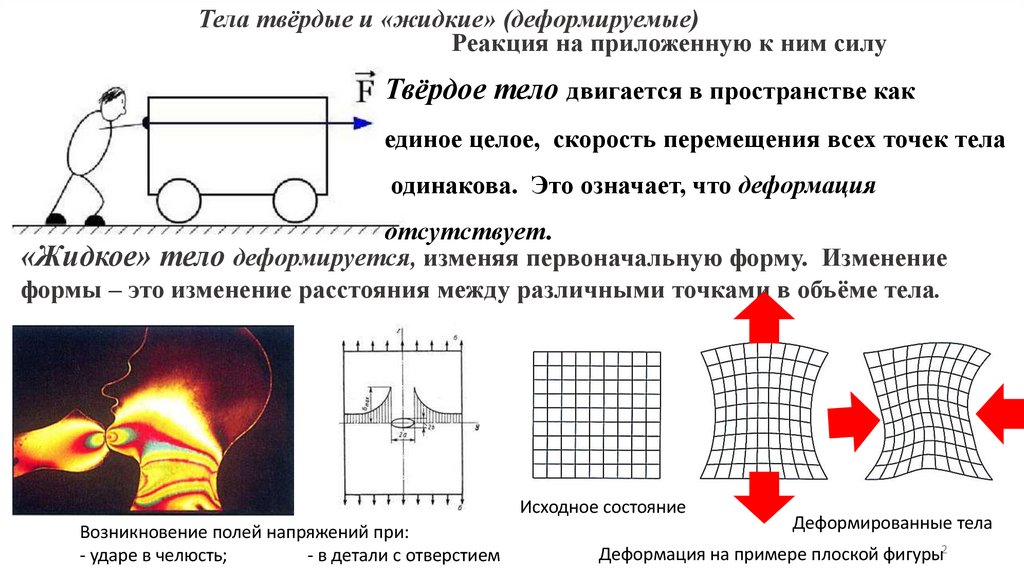
Тела твёрдые и «жидкие» (деформируемые)
Реакция на приложенную к ним силу
Твёрдое тело двигается в пространстве как
единое целое, скорость перемещения всех точек тела
одинакова. Это означает, что деформация
отсутствует.
«Жидкое» тело деформируется, изменяя первоначальную форму. Изменение
формы – это изменение расстояния между различными точками в объёме тела.
Исходное состояние
Возникновение полей напряжений при:
- ударе в челюсть;
- в детали с отверстием
Деформированные тела
Деформация на примере плоской фигуры2

3.

Что изучает реология?
Реология (от греч. ρέος, «течение, поток» и -логия) — раздел механики сплошных тел,
изучающий деформации и текучесть вещества под действием напряжения. Реология изучает
свойства вещества, трактуя эти свойства, как соотношение между напряжениями и
деформациями. При этом предполагают, что существует непрерывный переход от одной точки
среды к другой т.е. среда сплошная, непрерывная.
Задачи реологических исследований:
-Определение типа течения;
-Реологическое моделирование, позволяющее получить материальные функции для данной жидкости
при данных условиях течения;
-Экспериментальное определение реологических свойств;
- Установление зависимости между механическими напряжениями Р и деформациями ε, а также их
изменениями во времени t.
3

4.

Основные понятия и определения
Реологические свойства:
1) Упругость – способность тела восстанавливать первоначальные размеры после снятия нагрузки.
2) Прочность – способность тела сопротивляться приложенной нагрузке.
Еще одно свойство, которым могут обладать среды, изучаемые реологией, – это высокоэластичность,
характерная, например, для резины, когда резиновая лента допускает десятикратное растяжение, а после
снятия нагрузки практически мгновенно восстанавливает первоначальное состояние.
3) Вязкость – это свойство жидкости (или дисперсной системы) оказывать сопротивление ее течению под
действием сдвига.
4) Деформация - относительное смещение точек системы, при котором не нарушается ее сплошность (тело не
разрушается).
Деформация бывает двух видов:
Упругая деформация, характерная для твердых тел (обратимая). Она полностью исчезает
практически сразу после снятия нагрузки (пример - пружина)
Остаточная деформациям необратима, изменения в системе остаются и после снятия нагрузки
(свойственна пластичнымсистемам).
5) Пластичность – свойство тел развивать необратимые истинно остаточные деформации.
Следует отметить, что пластичность может наблюдаться, начиная с некоторой нагрузки, называемой пределом
текучести Рпред (при малых нагрузках система может проявлять упругие свойства), после которой
устанавливается течение с постоянной скоростью.
Вязкие тела отличаются от пластичных тем, что текут при любом напряжении. Для них предел текучести
равен нулю (Рпред = 0).
Течение - один из видов остаточной деформации, когда величина деформации постоянно увеличивается под
4
действием постоянной нагрузки. Такой вид деформации характерен для жидкостей и газов.

5.

Быстро текущая
(турбулентное течение)
Аксиомы реологии
Первая аксиома
Различия в реологических свойствах проявляются только при деформации, изменяющей
форму тела (деформации формоизменения).
Однако:Под действием всестороннего (изотропного) давления все материалы ведут
себя одинаково - как идеально упругие тела.
Вторая аксиома
У одного и того же материала в зависимости от его состояния и условий нагружения
могут проявляться в большей или меньшей мере различные реологические свойства.
Вода
Медленно текущая
Быстро текущая
(турбулентное течение)
Струя пробитая пулей
5
(разлетается как стекло

6.

Любое описание явлений в природе или социуме мы основываем на модельных представлениях.
Модель - это феноменологическое, чаще всего полученное в результате анализа известных фактов,
описание, связывающее наиболее значимые и характерные элементы явления.
Часто создают модели физические – в их основе лежит предположение, о том, что явление описывается
какими-то известными физическими законами.
При создании модели пренебрегают факторами, которые представляются менее значимыми. Некоторые
факторы бывают скрыты для исследователя при составлении модели. Обычно в ходе создания модели они
появляются в виде коэффициентов, которым придают некий физический смысл. Рассмотрение этих
коэффициентов – это следующий этап познания и совершенствования модели, увеличения её достоверности.
Поэтому принцип описания явлений с помощью моделей, которые кажутся универсальными, в
действительности всегда оказывается ограниченным, и «мелкие» подробности, не учитываемые основной
моделью, могут привести к неожиданным последствиям.
6

7.

Идеальные законы реологии
В реологии механические свойства материалов представляют в виде реологических моделей, в основе которых лежат
три основных идеальных закона, связывающих напряжение с деформацией. Им соответствуют три элементарные
модели (элемента) идеализированных материалов, отвечающих основным реологическим характеристикам (упругость,
пластичность, вязкость):
Деформация
- идеально упругое тело Гука (пружина),
E
= const
=
Время
- идеально вязкое тело Ньютона (поршень с отверстиями,
помещенный в цилиндр с жидкостью). Напряжение
сдвига при ламинарном течении жидкости с вязкостью η
пропорционально градиенту ее скорости деформации
- идеально пластическое тело Сен-Венана — Кулона (твердое
тело на поверхности, при движении которого трение постоянно
и не зависит от нормальной (перпендикулярной поверхности) силы) .
Деформация отсутствует до достижения напряжения, равного пределу
текучести: Р < PT значения γ = 0 и dγ / dτ = = 0
После достижения предела текучести деформация может
происходить с любой скоростью: PT < Рзначения γ ≥ 0 и dγ / dτ = > 0
Где: P- напряжение; PT – предел текучести.
Деформация
пластичного
материала
Зависимость деформации
от сдвигового напряжения
7

8.

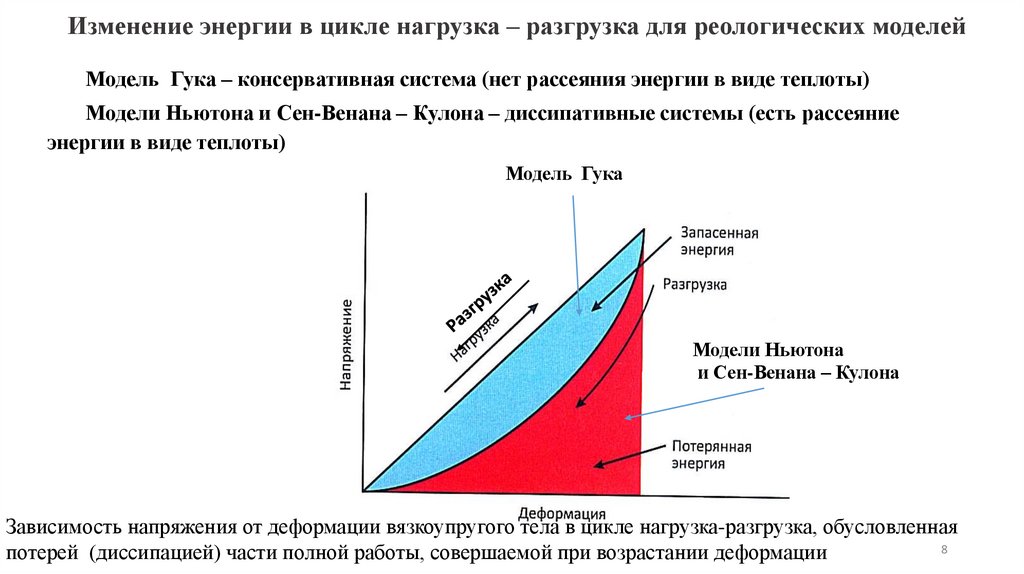
Изменение энергии в цикле нагрузка – разгрузка для реологических моделей
Модель Гука – консервативная система (нет рассеяния энергии в виде теплоты)
Модели Ньютона и Сен-Венана – Кулона – диссипативные системы (есть рассеяние
энергии в виде теплоты)
Модель Гука
Модели Ньютона
и Сен-Венана – Кулона
Зависимость напряжения от деформации вязкоупругого тела в цикле нагрузка-разгрузка, обусловленная
8
потерей (диссипацией) части полной работы, совершаемой при возрастании деформации

9.

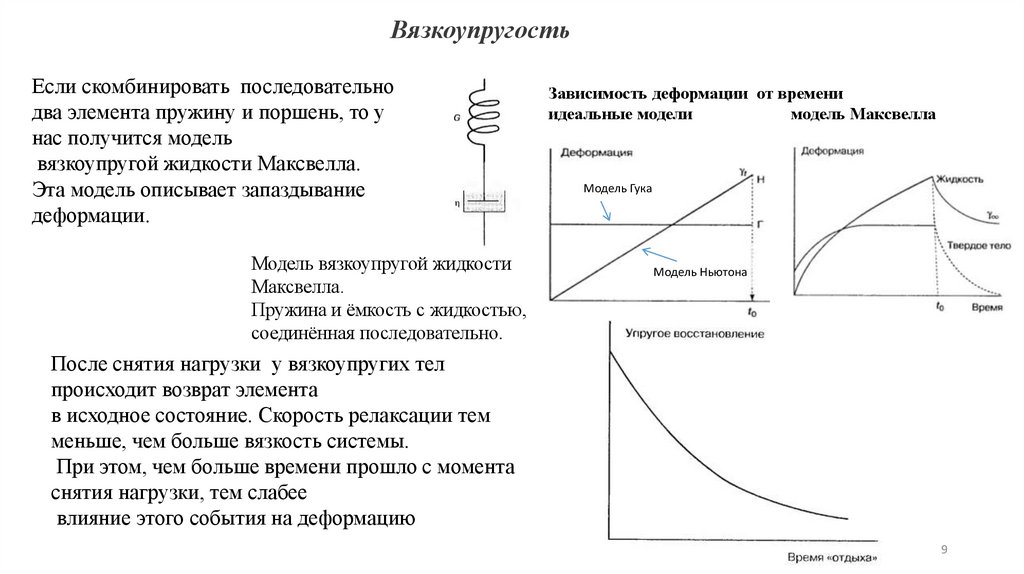
Вязкоупругость
Если скомбинировать последовательно
два элемента пружину и поршень, то у
нас получится модель
вязкоупругой жидкости Максвелла.
Эта модель описывает запаздывание
деформации.
Модель вязкоупругой жидкости
Максвелла.
Пружина и ёмкость с жидкостью,
соединённая последовательно.
Зависимость деформации от времени
идеальные модели
модель Максвелла
Модель Гука
Модель Ньютона
После снятия нагрузки у вязкоупругих тел
происходит возврат элемента
в исходное состояние. Скорость релаксации тем
меньше, чем больше вязкость системы.
При этом, чем больше времени прошло с момента
снятия нагрузки, тем слабее
влияние этого события на деформацию
9

10.

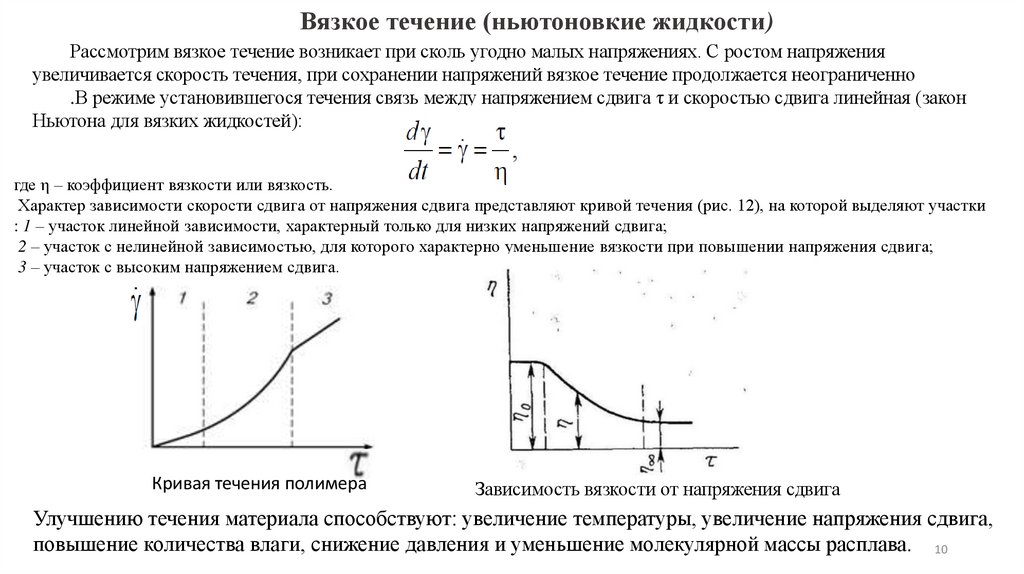
Вязкое течение (ньютоновкие жидкости)
Рассмотрим вязкое течение возникает при сколь угодно малых напряжениях. С ростом напряжения
увеличивается скорость течения, при сохранении напряжений вязкое течение продолжается неограниченно
.В режиме установившегося течения связь между напряжением сдвига τ и скоростью сдвига линейная (закон
Ньютона для вязких жидкостей):
где η – коэффициент вязкости или вязкость.
Характер зависимости скорости сдвига от напряжения сдвига представляют кривой течения (рис. 12), на которой выделяют участки
: 1 – участок линейной зависимости, характерный только для низких напряжений сдвига;
2 – участок с нелинейной зависимостью, для которого характерно уменьшение вязкости при повышении напряжения сдвига;
3 – участок с высоким напряжением сдвига.
Кривая течения полимера
Зависимость вязкости от напряжения сдвига
Улучшению течения материала способствуют: увеличение температуры, увеличение напряжения сдвига,
повышение количества влаги, снижение давления и уменьшение молекулярной массы расплава. 10

11.

Неньютоновские жидкости
Неньютоновскими жидкостями называют материалы, вязкость которых зависит от напряжения
сдвига, т.е. являются функцией скорости деформации (напряжения) в законе Ньютона.
1) Неньютоновские стационарные жидкости
Среди неньютоновских стационарных жидкостей различают псевдопластические и дилатантные. Типичные
зависимости скорости деформации жидкообразных тел от напряжения (кривые течения, или реологические
кривые) представлены на рис.
n = 1, k = : ньютоновская жидкость
n<1
для псевдопластических жидкостей
характерно снижение ньютоновской вязкости с
ростом скорости деформации сдвига
n>1
для дилатантных жидкостей
ньютоновская вязкость растет с увеличением скорости
деформации сдвига
Зависимость скорости деформации
от сдвигового напряжения
11

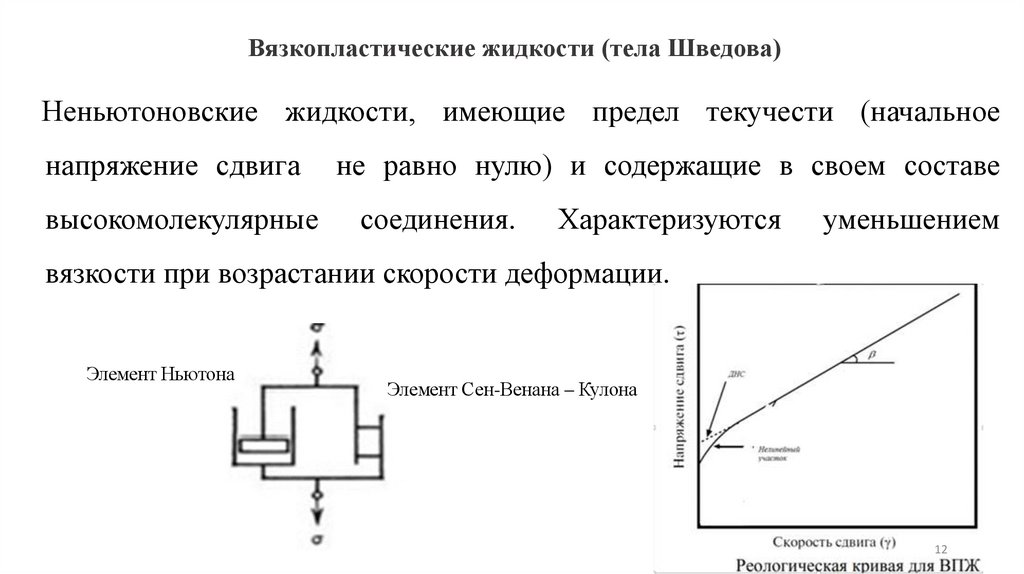
12. Вязкопластические жидкости (тела Шведова)

Неньютоновские жидкости, имеющие предел текучести (начальное
напряжение сдвига
высокомолекулярные
не равно нулю) и содержащие в своем составе
соединения.
Характеризуются
уменьшением
вязкости при возрастании скорости деформации.
Элемент Ньютона
Элемент Сен-Венана – Кулона
12

13.

Псевдопластичные жидкости
Для псевдопластичных жидкостей характерно уменьшение вязкости с увеличением
напряжения или скорости сдвига. В данном случае напряжение сдвига растет медленнее,
чем скорость сдвига, и угол наклона касательной к кривой уменьшается. К
псевдопластичным
жидкостям
относятся
некоторые
суспензии,
содержащие
асимметричные частицы. Проявление аномалии вязкости, в данном случае уменьшение ее
с ростом скорости сдвига, объясняется тем, что с увеличением скорости течения
асимметричные частицы постепенно ориентируются. При этом вязкость убывает до тех
пор, пока сохраняется возможность дальнейшего ориентирования частиц, а затем
зависимость напряжения от градиента скорости становится линейной.
Свойствами псевдопластичных жидкостей обладают также растворы и расплавы
большинства полимеров. Однако для них аномалия вязкости обусловлена строением
Скорость сдвига от
напряжения
макромолекул и характером надмолекулярных образований, возникающих в расплаве.
Для расплавов полимеров характерно также изменение степени аномалии вязкости в
зависимости от скорости сдвига, т. е. изменение вязкости при различных скоростях
сдвига неодинаково.
Вязкость от напряжения
13

14.

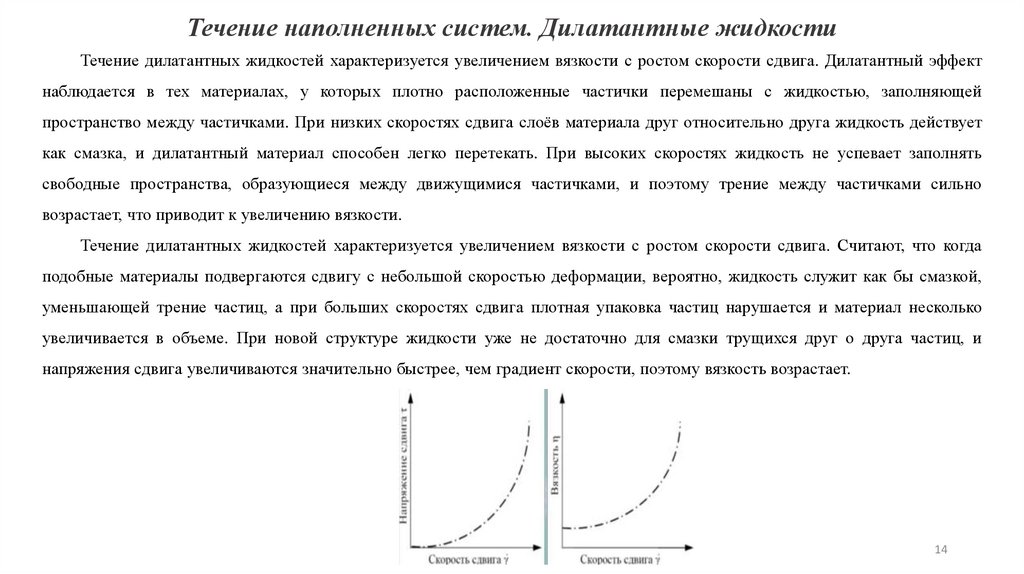
Течение наполненных систем. Дилатантные жидкости
Течение дилатантных жидкостей характеризуется увеличением вязкости с ростом скорости сдвига. Дилатантный эффект
наблюдается в тех материалах, у которых плотно расположенные частички перемешаны с жидкостью, заполняющей
пространство между частичками. При низких скоростях сдвига слоёв материала друг относительно друга жидкость действует
как смазка, и дилатантный материал способен легко перетекать. При высоких скоростях жидкость не успевает заполнять
свободные пространства, образующиеся между движущимися частичками, и поэтому трение между частичками сильно
возрастает, что приводит к увеличению вязкости.
Течение дилатантных жидкостей характеризуется увеличением вязкости с ростом скорости сдвига. Считают, что когда
подобные материалы подвергаются сдвигу с небольшой скоростью деформации, вероятно, жидкость служит как бы смазкой,
уменьшающей трение частиц, а при больших скоростях сдвига плотная упаковка частиц нарушается и материал несколько
увеличивается в объеме. При новой структуре жидкости уже не достаточно для смазки трущихся друг о друга частиц, и
напряжения сдвига увеличиваются значительно быстрее, чем градиент скорости, поэтому вязкость возрастает.
14

15.

Тиксотропия
Термин тиксотропия означает «чувствительный к прикосновению»,
а под тиксотропным эффектом понимают медленное изменение – обычно
уменьшение вязкости при деформации и отдыхом после снятия нагрузки.
Отличие между неньютоновским и тиксотропным поведением:
- неньютоновское –вязкость изменяется сразу, после приложения нагрузки
-
тиксотропное – вязкость изменяется в течение некоторого периода времени,
а после снятия нагрузки медленное полное или частичное возрастание вязкости
до начального уровня
Тиксотропное поведение в режиме «нагрузка – отдых»
Зависимость вязкости тиксотропного материала от времени
15

16.

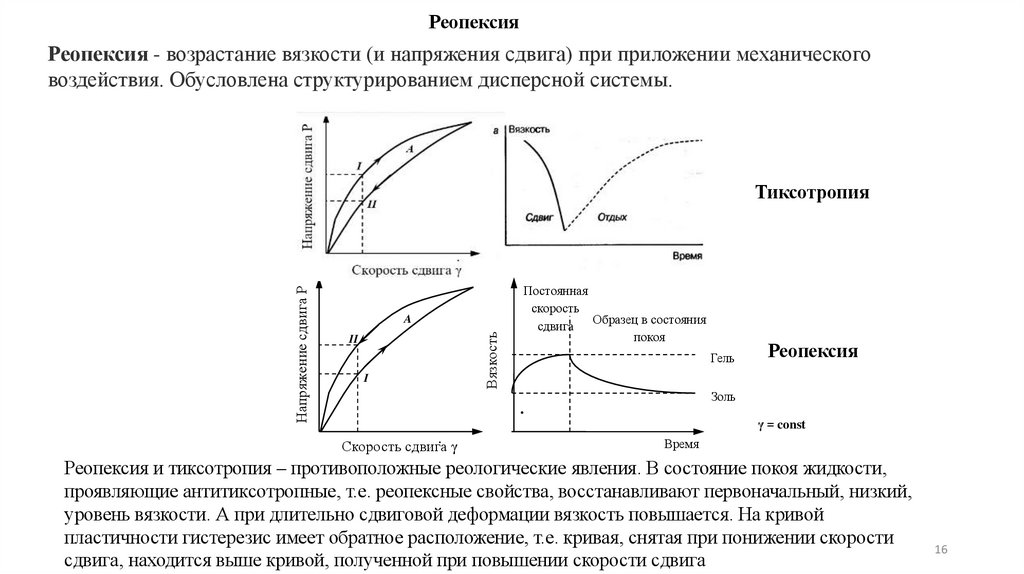
Реопексия
Реопексия - возрастание вязкости (и напряжения сдвига) при приложении механического
воздействия. Обусловлена структурированием дисперсной системы.
A
II
I
Вязкость
Напряжение сдвига Р
Тиксотропия
Постоянная
скорость
Образец в состояния
сдвига
покоя
Гель
Реопексия
Золь
.
.
Скорость сдвига γ
γ = const
Время
Реопексия и тиксотропия – противоположные реологические явления. В состояние покоя жидкости,
проявляющие антитиксотропные, т.е. реопексные свойства, восстанавливают первоначальный, низкий,
уровень вязкости. А при длительно сдвиговой деформации вязкость повышается. На кривой
пластичности гистерезис имеет обратное расположение, т.е. кривая, снятая при понижении скорости
сдвига, находится выше кривой, полученной при повышении скорости сдвига
16

17.

Чем определяет реологическое поведение полимера
Реологическое поведение полимеров определяется природой полимера (жёсткостью цепи, наличием боковых
групп, их полярностью), его молекулярной массой и молекулярно-массовым распределением, а также
температурой, напряжением и скоростью сдвига, при которых осуществляется течение раствора или расплава.
Поэтому нельзя характеризовать реологические свойства полимера по одной величине, скажем, по вязкости
Охарактеризовать реологическое поведение полимера можно, лишь установив зависимость вязкости от
напряжения или от скорости сдвига, либо зависимость напряжения сдвига от скорости сдвига и получив при
этом кривые течения.
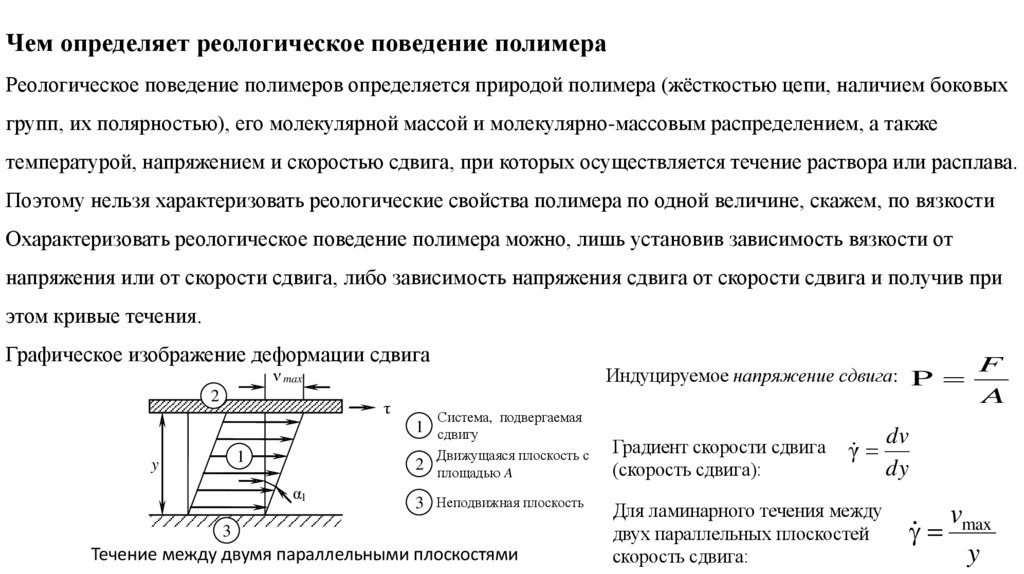
Графическое изображение деформации сдвига
Индуцируемое напряжение сдвига: P
ν max
2
τ
Система, подвергаемая
1 сдвигу
Движущаяся плоскость с
1
y
2 площадью A
α1
F
A
3 Неподвижная плоскость
3
Течение между двумя параллельными плоскостями
Градиент скорости сдвига
(скорость сдвига):
dv
γ
dy
Для ламинарного течения между
двух параллельных плоскостей
скорость сдвига:
vmax
y

18.

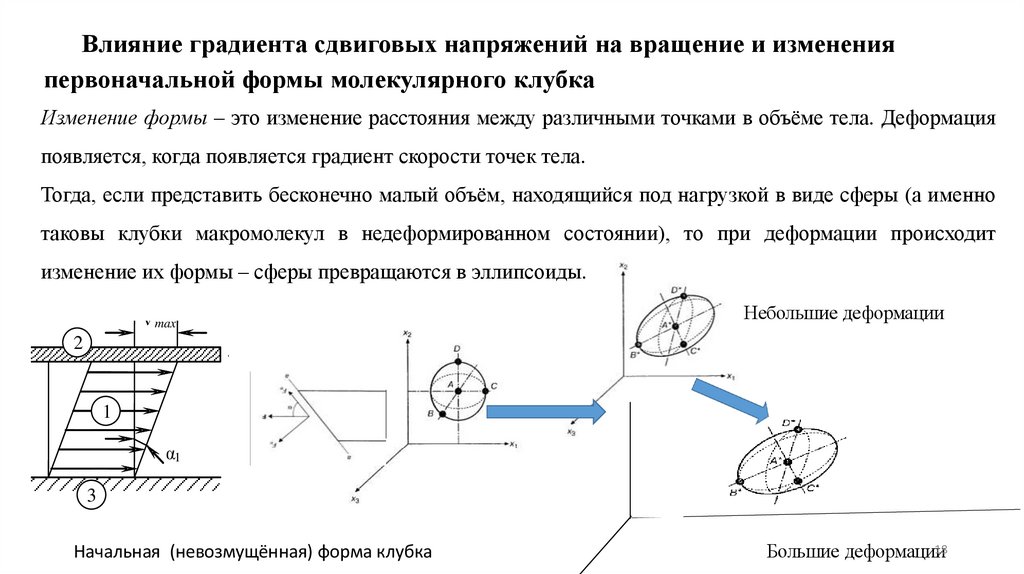
Влияние градиента сдвиговых напряжений на вращение и изменения
первоначальной формы молекулярного клубка
Изменение формы – это изменение расстояния между различными точками в объёме тела. Деформация
появляется, когда появляется градиент скорости точек тела.
Тогда, если представить бесконечно малый объём, находящийся под нагрузкой в виде сферы (а именно
таковы клубки макромолекул в недеформированном состоянии), то при деформации происходит
изменение их формы – сферы превращаются в эллипсоиды.
Небольшие деформации
ν max
2
τ
Система, подвергаемая
1 сдвигу
Движущаяся плоскость с
1
y
2 площадью A
α1
3 Неподвижная плоскость
3
Начальная (невозмущённая) форма клубка
18
Большие деформации

19.

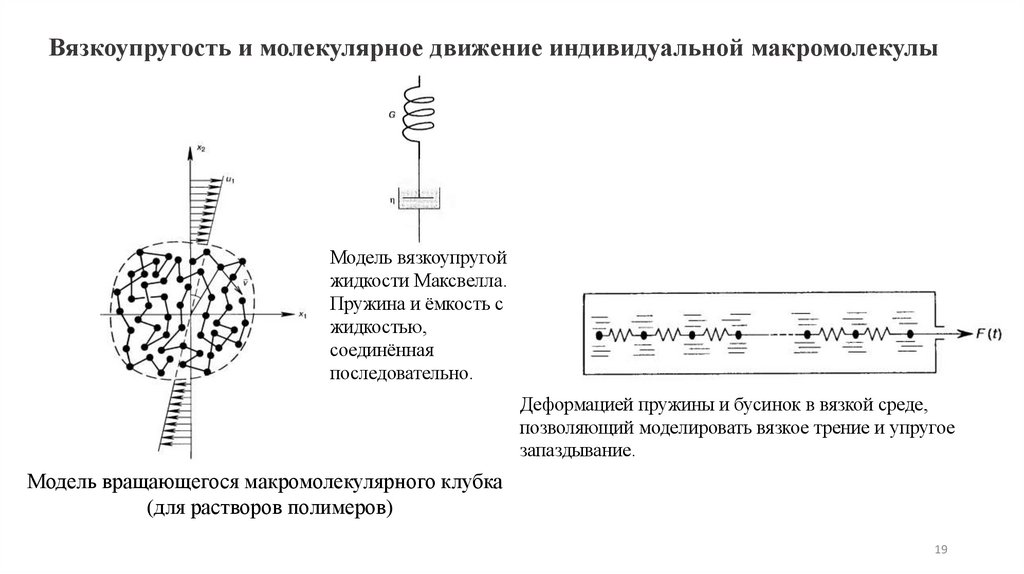
Вязкоупругость и молекулярное движение индивидуальной макромолекулы
Модель вязкоупругой
жидкости Максвелла.
Пружина и ёмкость с
жидкостью,
соединённая
последовательно.
Деформацией пружины и бусинок в вязкой среде,
позволяющий моделировать вязкое трение и упругое
запаздывание.
Модель вращающегося макромолекулярного клубка
(для растворов полимеров)
19

20.

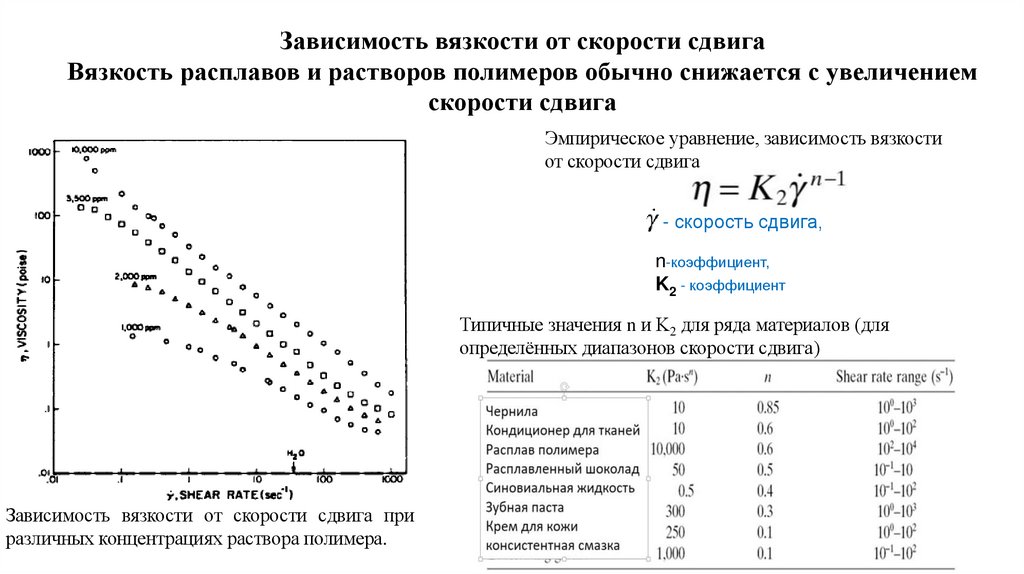
Зависимость вязкости от скорости сдвига
Вязкость расплавов и растворов полимеров обычно снижается с увеличением
скорости сдвига
Эмпирическое уравнение, зависимость вязкости
от скорости сдвига
- скорость сдвига,
n-коэффициент,
K2 - коэффициент
Типичные значения n и K2 для ряда материалов (для
определённых диапазонов скорости сдвига)
Зависимость вязкости от скорости сдвига при
различных концентрациях раствора полимера.
20

21.

Самоорганизации вязкоупругих жидкостей при высоких скоростях сдвига
Явление срыва
При высоких скоростях сдвига имеет место переход от гомогенного течения к гетерогенным
деформациям; в результате чего, становится возможной самоорганизация частиц в потоке,
сопровождаемая формированием периодических структур через неустойчивости различного вида и
дезинтеграцию среды на отдельные элементы. поведение среды при высоких скоростях деформации
следует рассматривать как последовательность комбинаций дискретных упругих элементов, которые
механически взаимодействуют друг с другом. В гипотетическом, неискаженном ("начальном")
состоянии первичные элементы – это сферические частицы, но они приобретают эллипсоидальную
форму под действием внешних сил и взаимных столкновений.
На кривой зависимости скорости сдвига от напряжения при
некотором напряжении наблюдается резкое возрастание
скорости сдвига. Этот эффект называют «срывом». Срыв
Вытягивание
характеризует переход от текучего состояния в
вынужденноластическое состояние. При высоких скоростях
Деформаци
деформирования монодисперсных полимеров они
я
переходят в вынужденное высокоэластическое состояние, и
их поведение становится подобным деформированию
Дезагрегация
высокоэластичных сред, в которых практически нет
Жидкости
течения, поэтому им можно пренебречь и нужно
Жидкости, текущие в направлении стрелок
в покое
рассматривать поведение среды как эластичного материала
Схема структуры жидкостей в покое и при приложении
Ориентация
сдвига.
21

22.

Ещё один аспект влияния скорости сдвига на вязкость расплава
Что такое вязкое течение? Какие тепловые эффекты происходят при течении по механизму вязкого течения?
Мы говорили, что упругая деформация происходит без диссипации энергии – сколько потрачено, столько
будет возвращено в систему. А вязкое течение диссипативно, т.е работа, потраченная на вязкое течение
рассеивается в виде тепла, т.е. происходит разогрев самого материала, в нашем случае- расплава полимера.
Скорость диссипации энергии в единице объема при сдвиге может выражаться либо как произведение
напряжения сдвига и скорости сдвига, либо, эквивалентна произведению вязкости и квадрату скорости
сдвига.
Wвяз 2
Разогрев расплава полимера при вязком течении может быть значителен. Таким образом, выделившееся тепло
разогревая материал, фактически уменьшает его измеряемую вязкость, если вязкость высокая или скорость
сдвига большая, то количество выделившегося тепла велико.
С инженерной точки зрения это выражается в разогреве массы при смешении. Поэтому в хороших
экструдерах для поддержания температурного режима смешения и предотвращения перегрева массы кроме
нагревателей каждая зона снабжена системой охлаждения. Обычно охлаждение осуществляют впрыском
струй воды на наружную стенку камеры смешения.
22

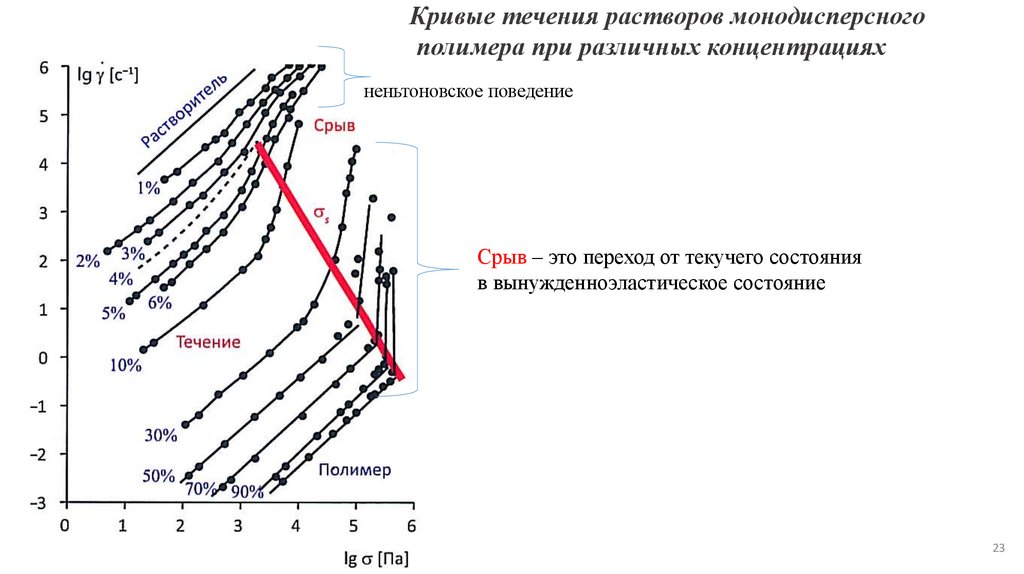
23.

Кривые течения растворов монодисперсного
полимера при различных концентрациях
неньтоновское поведение
Срыв – это переход от текучего состояния
в вынужденноэластическое состояние
23

24.

Зависимость вязкости расплавов полимеров от ММ
Полимеры
Критические значения (Мс) для некоторых полимеров
Низкомолекулярные
гомологи
«критическое» значение Мс
Область
перегиба
кривой
показывает
значение
молекулярной массы, при которой в полимере возникает
флуктуационная сетка зацеплений, образованная узлами
или
зацеплениями
макромолекул
или
ассоциатами
Кривые течения расплавов
сегментов макромолекул, возникающих в результате ван-
полимеров в зависимости от ММ
дер- ваальсова взаимодействия
24

25.

Температурная зависимость вязкости
Температурная зависимость вязкости определяется вероятностью перескока сегментов в зависимости
от температуры.
Сегментальная подвижность возрастает с увеличением тепловой энергии в системе и уменьшением
межмолекулярного взаимодействия. Это происходит при увеличении температуры полимера. Уравнение
Аррениуса для вязкости:
η = η₀e-E/R T
где: T-абсолютная температура, η₀ — вязкость при бесконечно большой температуре;
E — энергия активации вязкого течения (энергия, которую должна преодолеть частица жидкости для
перехода из одного равновесного состояния в другое);
R — универсальная газовая постоянная (R = 8,314 кДж/(моль·К));
Уравнение Аррениуса может быть применяться при температуре намного выше температуры
стеклования.
Энергия активации вязкого течения показывает, насколько сильно вязкость зависит от температуры, чем
больше энергия активации, которую сегмент должен получить для его отделения от других молекул, тем
сильнее снижается вязкость с ростом температуры.
25

26.

Влияние эластичности на течение полимеров
При небольших скоростях течении расплавов полимеров молекулярные клубки
деформируются мало. Повышение скорости течения приводит к:
- Растягиванию клубков, переводу их в упругодеформированное состояние; появлению
упругой составляющей, в результате чего снижается внутреннее трение и, поэтому,
снижается вязкость;
- Уменьшению количества внутри- и межмолекулярных связей, т.е. флуктуационной
сетки между молекулами, что также приводит к снижению вязкости. Такая
деформация называется «эластической»
- Искажение формы струи. Развитие больших высокоэластических деформаций
приводит к скольжению полимера по стенкам капилляра и срыву струи.
- эластические деформации релаксируют при выходе из капилляра (фильеры). Струя
полимера сокращается и разбухает. Чем больше запасается энергии при течении в
капилляре, тем больше разбухание струи.
Эти явления отсутствуют
Разбухание струи
у низкомолекулярных веществ.
Как только клубки окажутся предельно растянутыми весь поток полимера становится
26
нетекучим.

27.

Влияние эластичности на течение полимеров
Влияние скорости сдвига на время установления стационарного
течения жидкости
В зависимости от скорости сдвига зависимость напряжения
Скорость сдвига
3>2>1
сдвига от времени приложения (скорости приложения)
нагрузки может иметь различную форму:
Т.е. время установления стационарного течения жидкости
зависит (при постоянной вязкости) от скорости приложения
нагрузки. При низких скоростях приложения напряжения,
соизмеримых со скоростями релаксационных процессов в
полимере, равновесное течение устанавливается быстрее,
чем
при
больших
скоростях,
при
которых
для
формирования новой структуры в потоке на начальном
Зависимость напряжения сдвига от
времени при различных скоростях
сдвига
этапе затрачивается дополнительная энергия, величина
которой растёт с увеличением скорости сдвига.
27

28.

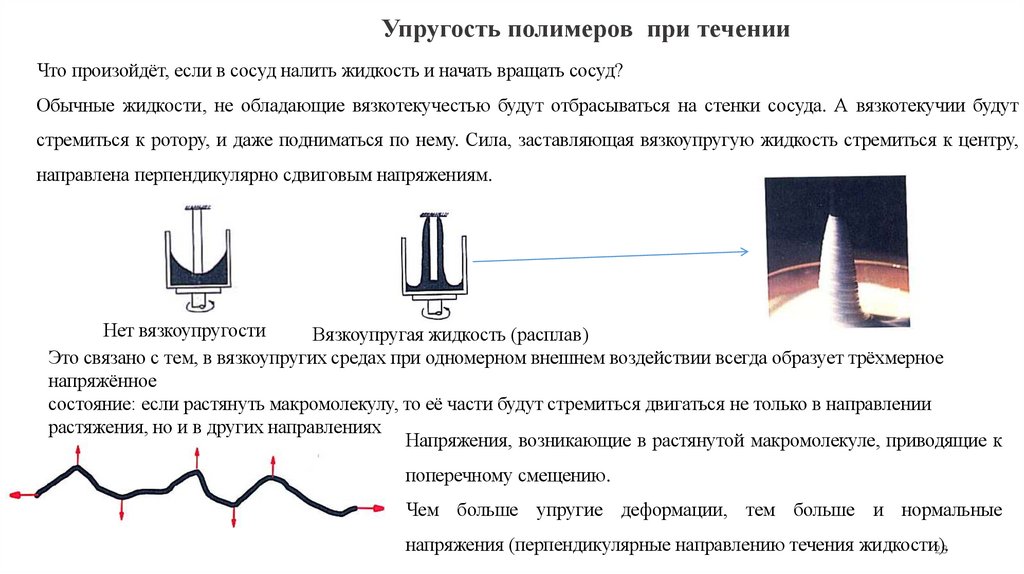
Упругость полимеров при течении
Что произойдёт, если в сосуд налить жидкость и начать вращать сосуд?
Обычные жидкости, не обладающие вязкотекучестью будут отбрасываться на стенки сосуда. А вязкотекучии будут
стремиться к ротору, и даже подниматься по нему. Сила, заставляющая вязкоупругую жидкость стремиться к центру,
направлена перпендикулярно сдвиговым напряжениям.
Нет вязкоупругости
Вязкоупругая жидкость (расплав)
Это связано с тем, в вязкоупругих средах при одномерном внешнем воздействии всегда образует трёхмерное
напряжённое
состояние: если растянуть макромолекулу, то её части будут стремиться двигаться не только в направлении
растяжения, но и в других направлениях
Напряжения, возникающие в растянутой макромолекуле, приводящие к
поперечному смещению.
Чем больше упругие деформации, тем больше и нормальные
напряжения (перпендикулярные направлению течения жидкости).
28

29.

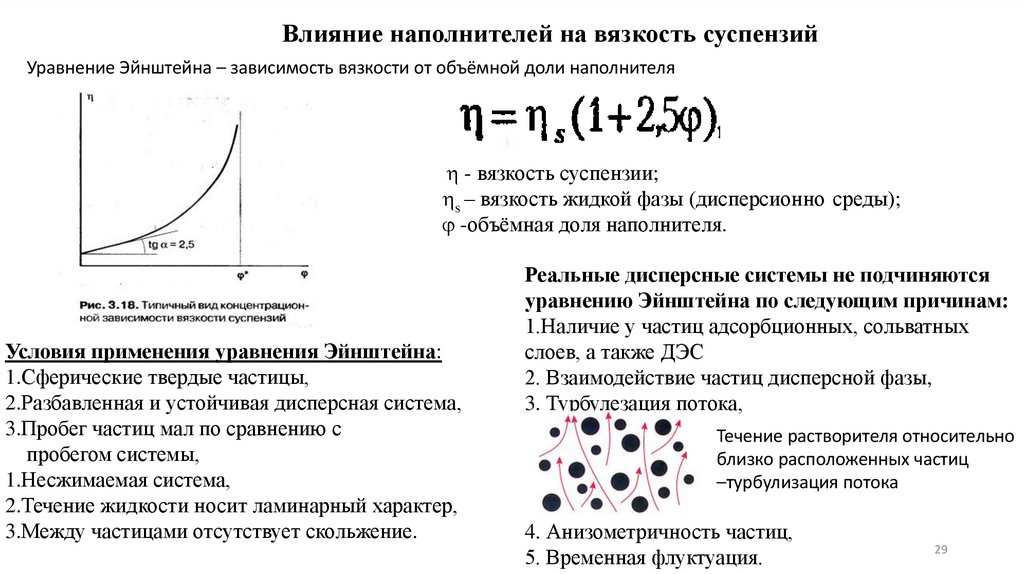
Влияние наполнителей на вязкость суспензий
Уравнение Эйнштейна – зависимость вязкости от объёмной доли наполнителя
- вязкость суспензии;
s – вязкость жидкой фазы (дисперсионно среды);
-объёмная доля наполнителя.
Условия применения уравнения Эйнштейна:
1.Сферические твердые частицы,
2.Разбавленная и устойчивая дисперсная система,
3.Пробег частиц мал по сравнению с
пробегом системы,
1.Несжимаемая система,
2.Течение жидкости носит ламинарный характер,
3.Между частицами отсутствует скольжение.
Реальные дисперсные системы не подчиняются
уравнению Эйнштейна по следующим причинам:
1.Наличие у частиц адсорбционных, сольватных
слоев, а также ДЭС
2. Взаимодействие частиц дисперсной фазы,
3. Турбулезация потока,
Течение растворителя относительно
близко расположенных частиц
–турбулизация потока
4. Анизометричность частиц,
5. Временная флуктуация.
29

30.

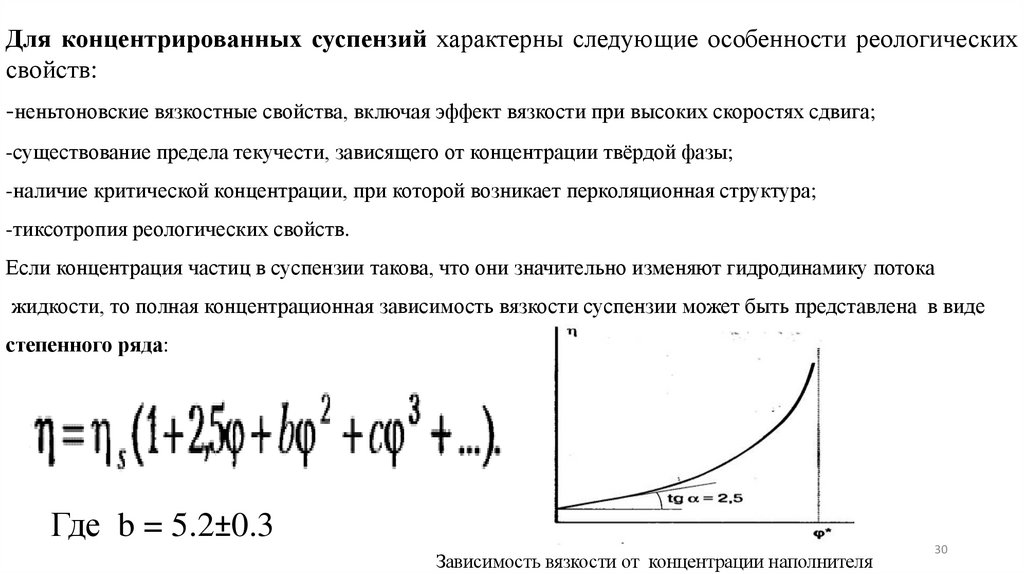
Для концентрированных суспензий характерны следующие особенности реологических
свойств:
-неньтоновские вязкостные свойства, включая эффект вязкости при высоких скоростях сдвига;
-существование предела текучести, зависящего от концентрации твёрдой фазы;
-наличие критической концентрации, при которой возникает перколяционная структура;
-тиксотропия реологических свойств.
Если концентрация частиц в суспензии такова, что они значительно изменяют гидродинамику потока
жидкости, то полная концентрационная зависимость вязкости суспензии может быть представлена в виде
степенного ряда:
Где b = 5.2±0.3
Зависимость вязкости от концентрации наполнителя
30

31.

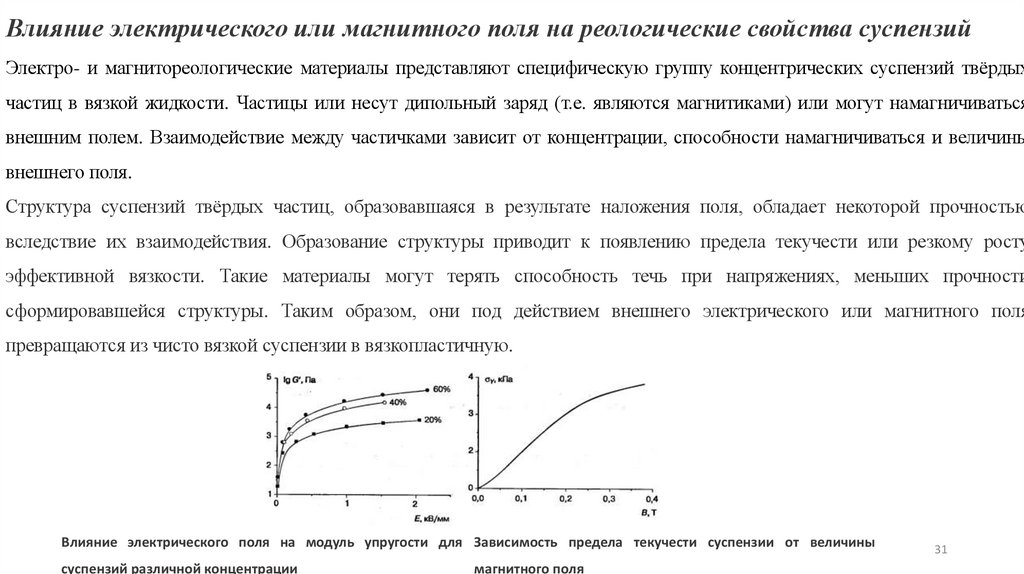
Влияние электрического или магнитного поля на реологические свойства суспензий
Электро- и магнитореологические материалы представляют специфическую группу концентрических суспензий твёрдых
частиц в вязкой жидкости. Частицы или несут дипольный заряд (т.е. являются магнитиками) или могут намагничиваться
внешним полем. Взаимодействие между частичками зависит от концентрации, способности намагничиваться и величины
внешнего поля.
Структура суспензий твёрдых частиц, образовавшаяся в результате наложения поля, обладает некоторой прочностью
вследствие их взаимодействия. Образование структуры приводит к появлению предела текучести или резкому росту
эффективной вязкости. Такие материалы могут терять способность течь при напряжениях, меньших прочности
сформировавшейся структуры. Таким образом, они под действием внешнего электрического или магнитного поля
превращаются из чисто вязкой суспензии в вязкопластичную.
Влияние электрического поля на модуль упругости для Зависимость предела текучести суспензии от величины
суспензий различной концентрации
магнитного поля
31

32.

Вязкость – сила трения, возникающая между двумя смежными слоями
внутри жидкости или газа на единице поверхности при их взаимном
перемещении
Различают кинематическую и динамическую вязкости.
Динамическая вязкость (μ ) характеризует сопротивления жидкости течению пр
Кинематической вязкостью (ν) называют отношение вязкости динамической к п
Единица измерения динамической вязкости - Пуаз
· 1 Пуаз = 1 дин·с/см2 = 0.010197162 кгс·с/м2 = 0.0000010197162 кгс·с/см2
= 0.1 Па·с = 0.1 Н·с/м2
· 1 Сантипуаз = 0.0001010197162 кгс·с/м = 0.01 П = 0.001 Па·с
· 1 кгс·с/м = 98.0665 П = 9806.65 сП = 9.80665 Па·с.
Единица измерения кинематической вязкости - Стокс
· 1 Ст = 0.0001 м /с = 1 см /с
· 1 сСт = 1 мм /с = 0.000001 м /с
· 1 м2/с = 10000 Ст = 1000000 сСт.
32

33. Приборы для оценки реологических свойств

Производственные
(технологические)
Условные методы
Исследовательские
Абсолютные методы
Определяемые показатели:
• Индекс расплава (показатель текучести, ПТР)
• Напряжение сдвига
• Вязкость
• Скорости сдвига
33

34.

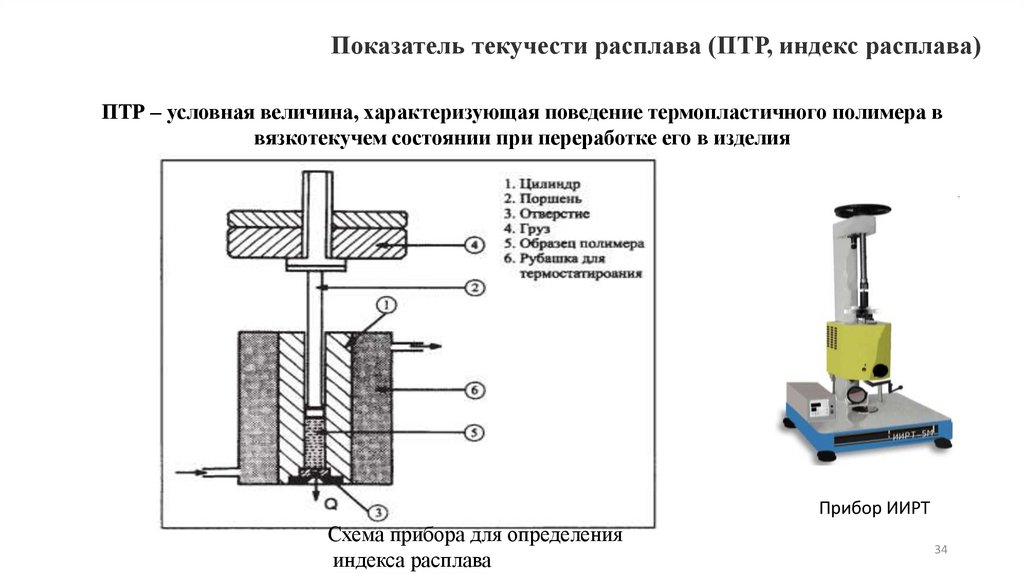
Показатель текучести расплава (ПТР, индекс расплава)
ПТР – условная величина, характеризующая поведение термопластичного полимера в
вязкотекучем состоянии при переработке его в изделия
Прибор ИИРТ
Схема прибора для определения
индекса расплава
34

35.

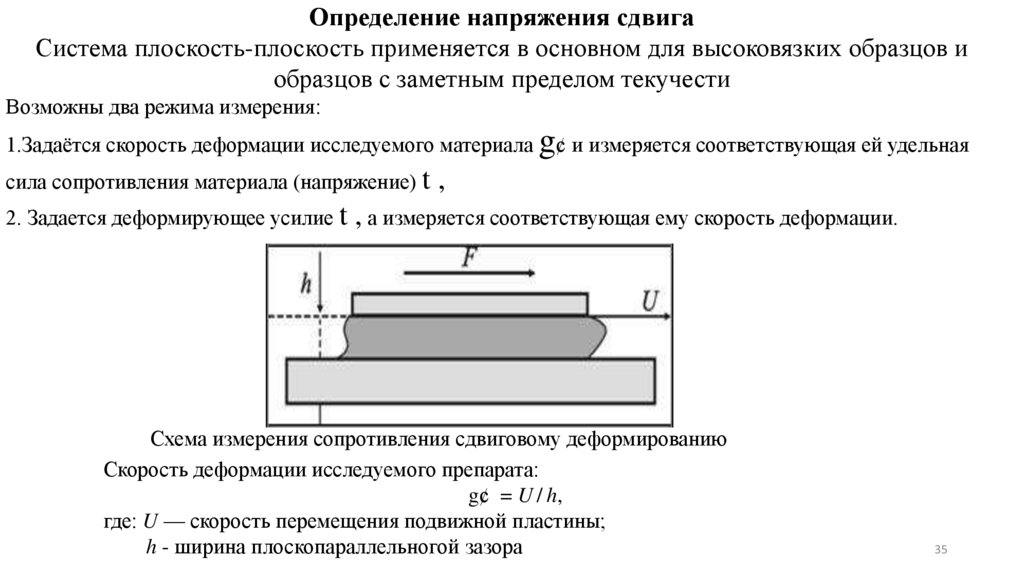
Определение напряжения сдвига
Система плоскость-плоскость применяется в основном для высоковязких образцов и
образцов с заметным пределом текучести
Возможны два режима измерения:
1.Задаётся скорость деформации исследуемого материала
g¢ и измеряется соответствующая ей удельная
сила сопротивления материала (напряжение) t ,
2. Задается деформирующее усилие t , а измеряется соответствующая ему скорость деформации.
Схема измерения сопротивления сдвиговому деформированию
Скорость деформации исследуемого препарата:
g¢ = U / h,
где: U — скорость перемещения подвижной пластины;
h - ширина плоскопараллельногой зазора
35

36.

РЕОМЕТРЫ
Ротационные реометры с различными типами измерительных ячеек:
коаксиальные (соосные) цилиндры, конус-плоскость, плоскость-плоскость.
Схема ротационного вискозиметра:
R — радиус внутреннего цилиндра; h
— зазор между внутренним и
внешним цилиндром; Н — глубина
погружения цилиндра в исследуемый
состав
Жидкий образец заполняет кольцевой зазор между цилиндрами и подвергается сдвигу в течение заданного
времени. Конструкция современных реометров обеспечивает ламинарное течение и позволяет проводить
математическую обработку результатов, представляя измеренные величины напряжений и скоростей
сдвига, а также вязкости в соответствующих физических величинах.
В абсолютных реометрах применяется два основных варианта вышеописанной геометрии измерительных
систем, которые позволяют:
– задавать напряжение и определять полученную в результате величину скорости сдвига; эти приборы
называют «реометрами с контролируемым напряжением, или CS-реометрами»;
– задавать скорость сдвига и определять полученное в результате этого напряжение сдвига; эти приборы
называют «реометры с контролируемой скоростью сдвига, или CR-реометры»;
36

37.

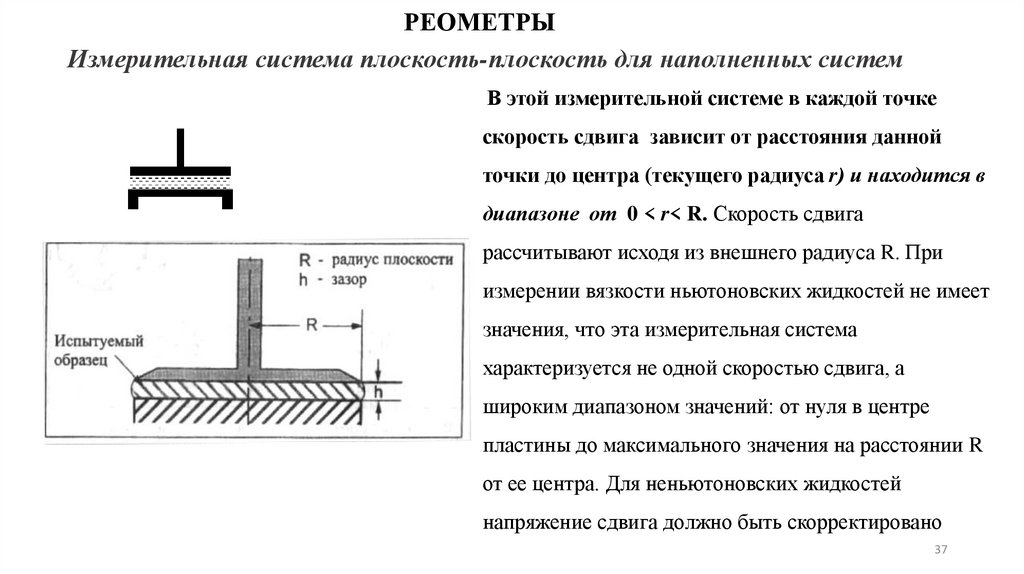
РЕОМЕТРЫ
Измерительная система плоскость-плоскость для наполненных систем
В этой измерительной системе в каждой точке
скорость сдвига зависит от расстояния данной
точки до центра (текущего радиуса r) и находится в
диапазоне от 0 < r< R. Скорость сдвига
рассчитывают исходя из внешнего радиуса R. При
измерении вязкости ньютоновских жидкостей не имеет
значения, что эта измерительная система
характеризуется не одной скоростью сдвига, а
широким диапазоном значений: от нуля в центре
пластины до максимального значения на расстоянии R
от ее центра. Для неньютоновских жидкостей
напряжение сдвига должно быть скорректировано
37

38.

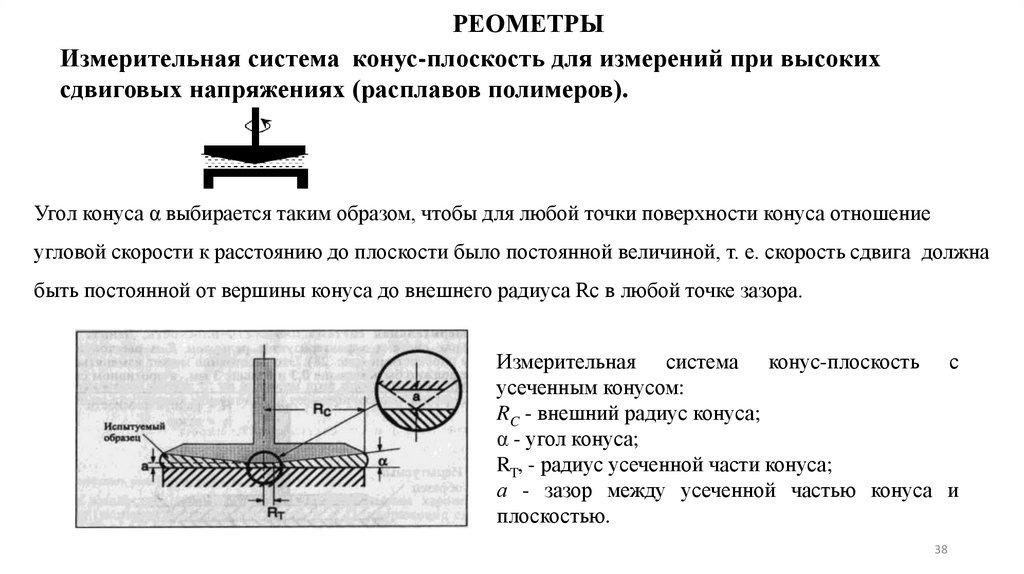
РЕОМЕТРЫ
Измерительная система конус-плоскость для измерений при высоких
сдвиговых напряжениях (расплавов полимеров).
Угол конуса α выбирается таким образом, чтобы для любой точки поверхности конуса отношение
угловой скорости к расстоянию до плоскости было постоянной величиной, т. е. скорость сдвига должна
быть постоянной от вершины конуса до внешнего радиуса Rс в любой точке зазора.
Измерительная система конус-плоскость с
усеченным конусом:
RC - внешний радиус конуса;
α - угол конуса;
RT, - радиус усеченной части конуса;
а - зазор между усеченной частью конуса и
плоскостью.
38

39.

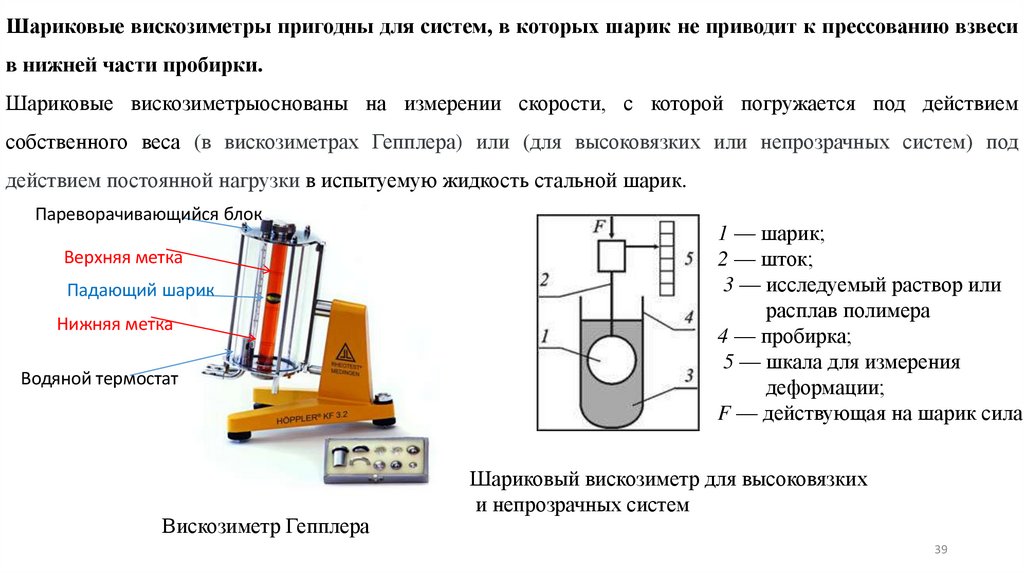
Шариковые вискозиметры пригодны для систем, в которых шарик не приводит к прессованию взвеси
в нижней части пробирки.
Шариковые вискозиметрыоснованы на измерении скорости, с которой погружается под действием
собственного веса (в вискозиметрах Гепплера) или (для высоковязких или непрозрачных систем) под
действием постоянной нагрузки в испытуемую жидкость стальной шарик.
Пареворачивающийся блок
Верхняя метка
Падающий шарик
Нижняя метка
Водяной термостат
Вискозиметр Гепплера
1 — шарик;
2 — шток;
3 — исследуемый раствор или
расплав полимера
4 — пробирка;
5 — шкала для измерения
деформации;
F — действующая на шарик сила
Шариковый вискозиметр для высоковязких
и непрозрачных систем
39