Конечные автоматы и регулярные языки. Лекция 12

1. Конечные автоматы и регулярные языки Лекция 12

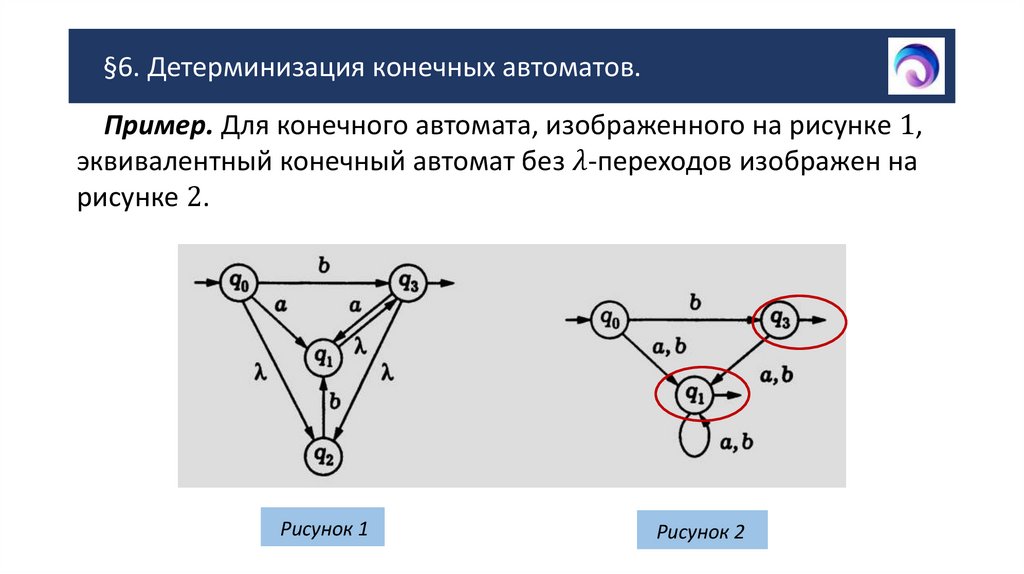
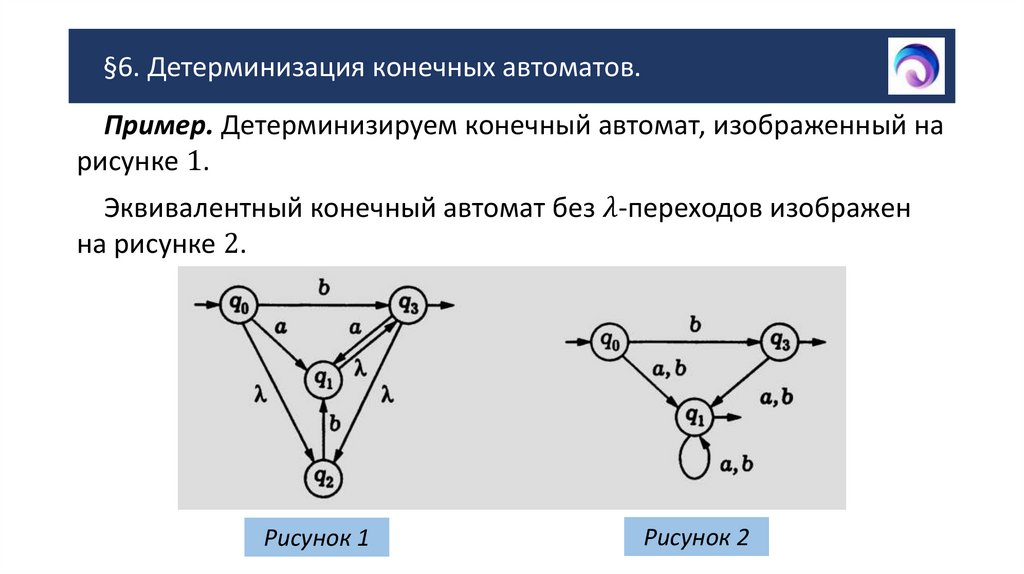
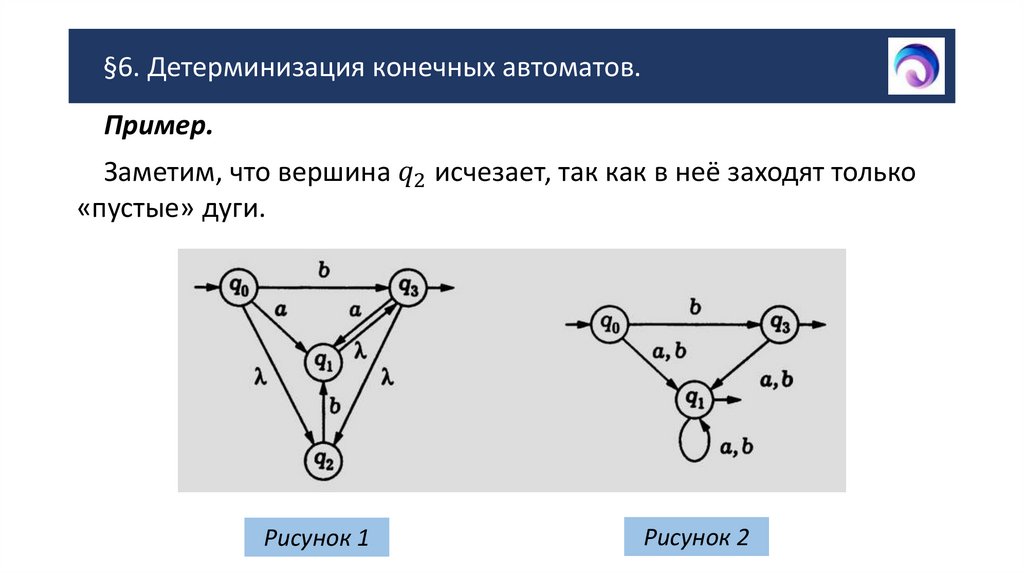
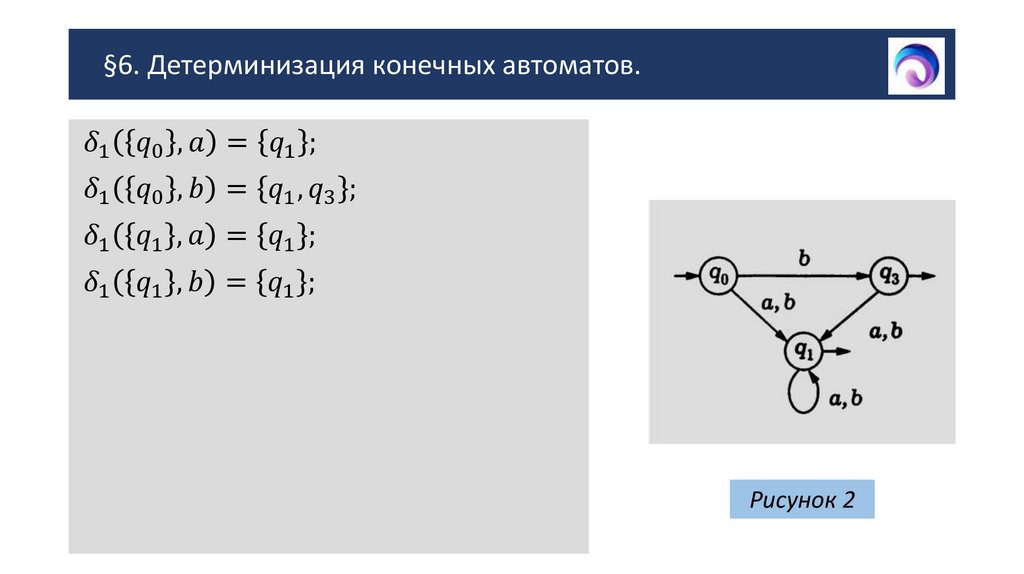
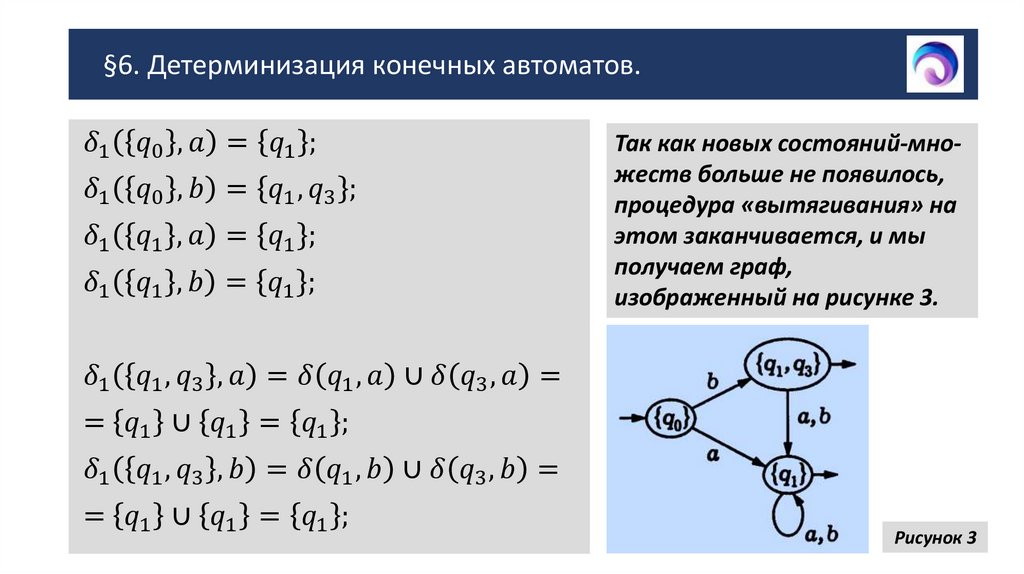
§6. Детерминизация конечных автоматов.

2. §6. Детерминизация конечных автоматов.

Для решения задачи синтеза конечных автоматов важное
значение имеет следующая теорема.
Теорема 5 (теорема о детерминизации). Для любого кoнeчнoгo
автомата может быть построен эквивалентный ему детерминированный конечный автомат.
Доказательство. Для того чтобы доказать теорему, нужно, вопервых, описать алгоритм построения детерминированного
конечного автомата по исходному конечному автомату; во-вторых,
обосновать этот алгоритм, строго доказав, что он действительно
дает конечный автомат, который является детерминированным и
эквивалентным исходному. Здесь мы приведем только сам
алгоритм построения детерминированного автомата.

3. §6. Детерминизация конечных автоматов.

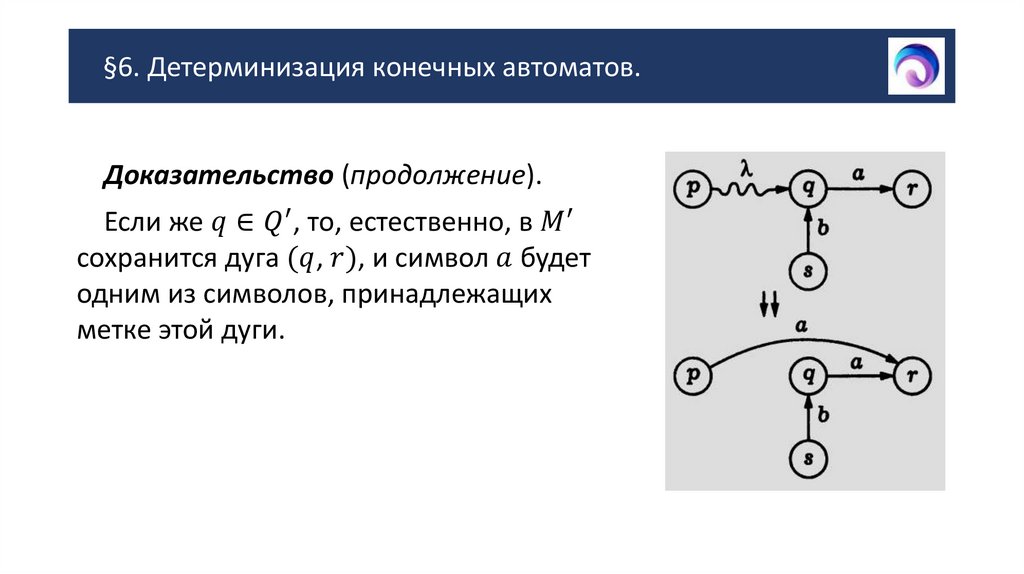
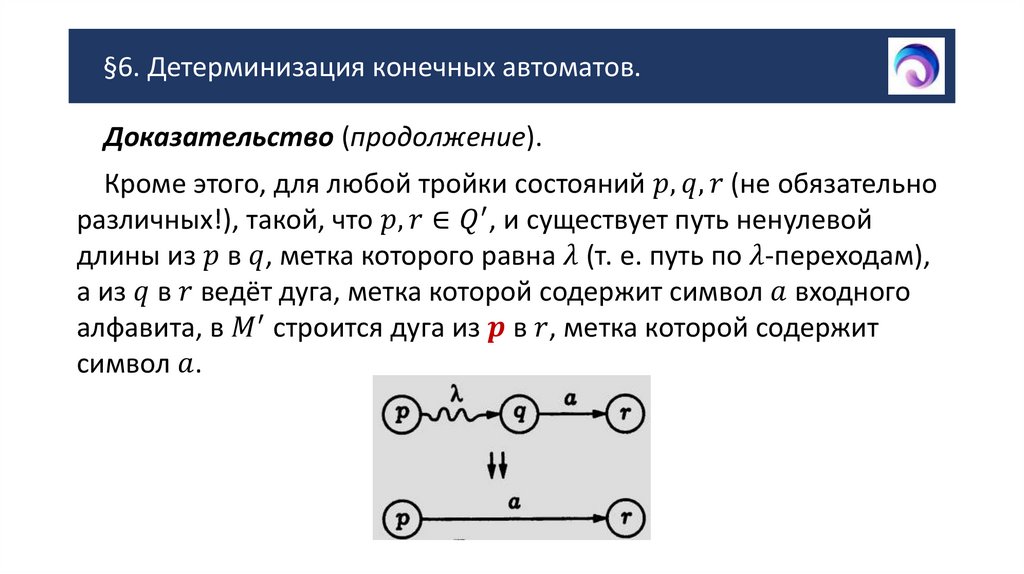
Доказательство (продолжение).
Преобразование произвольного конечного автомата к
эквивалентному детерминированному автомату осуществляется в
два этапа: сначала удаляются дуги с меткой