Algorithms and Data structure Lecture 5 – Hash Tabel and BST (Part i)

1. Algorithms and Data structure Lecture 5 – Hash Tabel and BST (Part i)

ALGORITHMS AND DATA STRUCTURE
LECTURE 5 – HASH TABEL AND BST (PART I)
Aigerim Aibatbek, Eldiyar Zhantileuov
aigerim.aibatbek@astanait.edu.kz, zhantileuov.eldiyar@astanait.edu.kz

2. content

CONTENT
1.
Hashing
2.
Hash Table
3.
Binary Search Tree
4.
BST: Inorder Traversal
2

3. Hashing

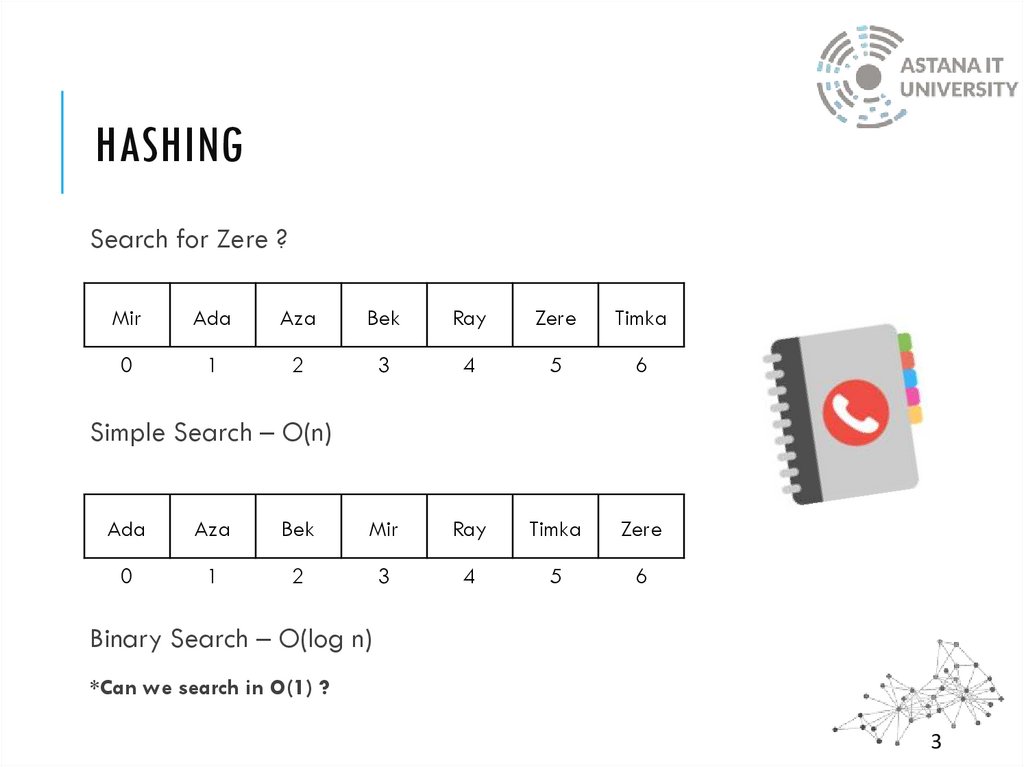
HASHING
Search for Zere ?
Mir
Ada
Aza
Bek
Ray
Zere
Timka
0
1
2
3
4
5
6
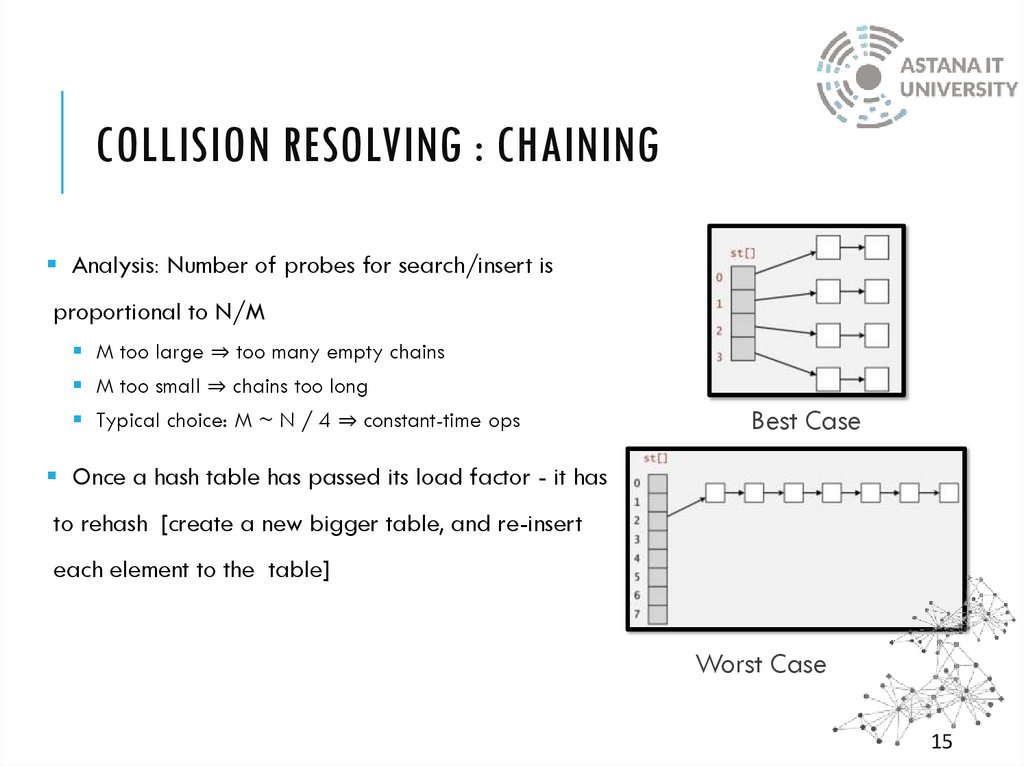
Simple Search – O(n)
Ada
Aza
Bek
Mir
Ray
Timka
Zere
0
1
2
3
4
5
6
Binary Search – O(log n)
*Can we search in O(1) ?
3

4. Hashing

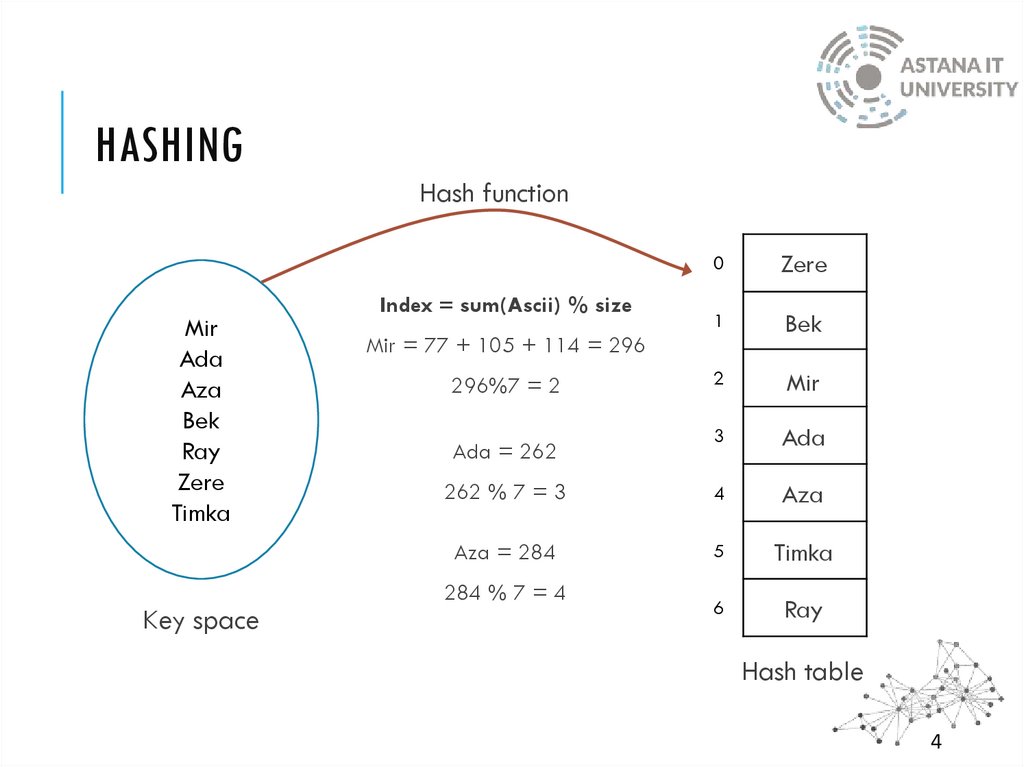
HASHING
Hash function
Mir
Ada
Aza
Bek
Ray
Zere
Timka
0
Zere
1
Bek
2
Mir
3
Ada
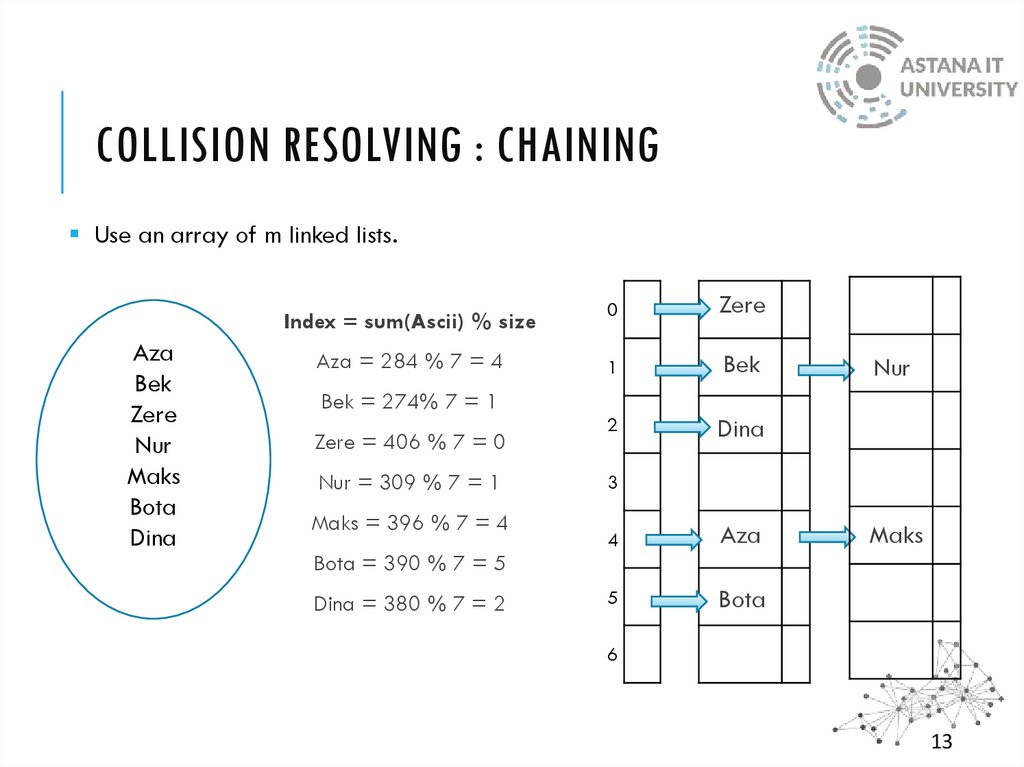
262 % 7 = 3
4
Aza
Aza = 284
5
Timka
6
Ray
Index = sum(Ascii) % size
Mir = 77 + 105 + 114 = 296
296%7 = 2
Ada = 262
284 % 7 = 4
Key space
Hash table
4

5. Hashing

HASHING
0
Zere
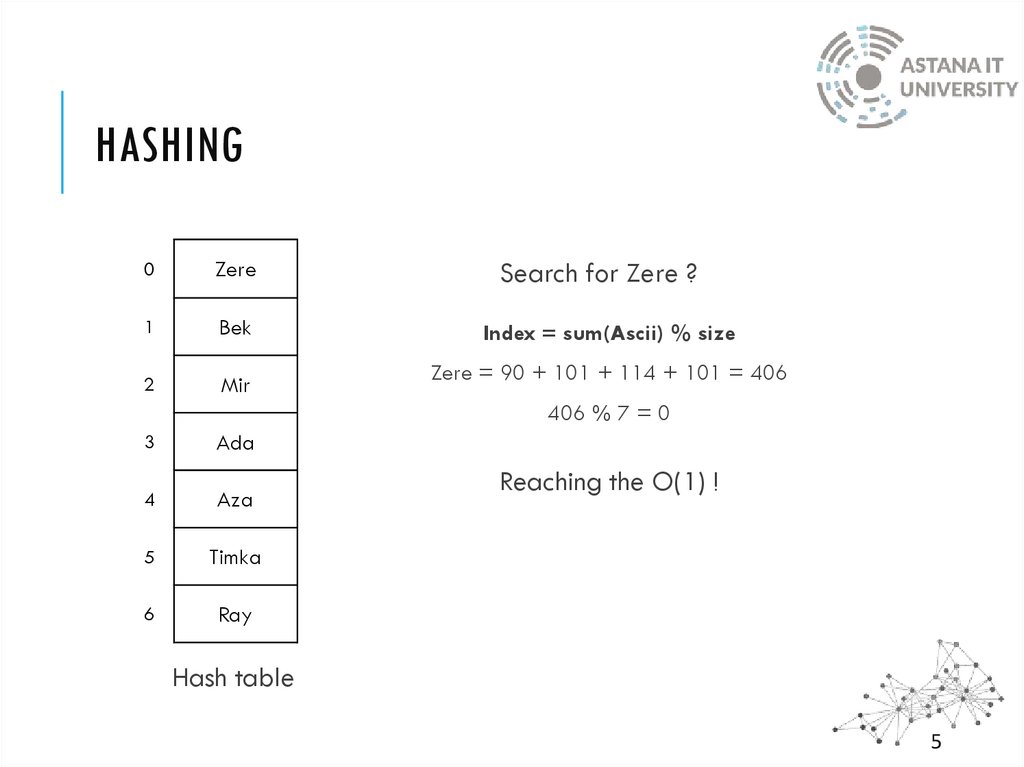
Search for Zere ?
1
Bek
Index = sum(Ascii) % size
2
Mir
Zere = 90 + 101 + 114 + 101 = 406
406 % 7 = 0
3
Ada
4
Aza
5
Timka
6
Ray
Reaching the O(1) !
Hash table
5

6. Hashing

HASHING
Hashing means using some function or algorithm to map object data to
some representative integer value
This so-called hash code (or simply hash) can then be used as a way to
narrow down our search when looking for the item in the set
Object class contains hashCode() method with its default implementation
Each class provides its own implementation of hashCode()
6

7. Implementing HashCode(): STRING EXAMPLE

IMPLEMENTING HashCode(): STRING EXAMPLE
Horner's method to hash string of length L: Lmultiplies/adds.
Equivalent to ℎ =