Исследование устойчивости динамической системы электропривода

1.

Институт Информационных Технологий Математики и Механики
Кафедра: Прикладной математики
Направление: Прикладная математика и информатика
ВЫПУСКНАЯ КВАЛИФИКАЦИОННАЯ РАБОТА БАКАЛАВРА
Тема:
«Исследование устойчивости динамической
системы электропривода»
Заведующий кафедрой:
Профессор, д.ф.-м.н. Иванченко М.В.
Выполнила: студентка группы в0853
Лутошкина А.М.
Научный руководитель:
доцент кафедры прикладной математики,
к.т.н. Стребуляев С.Н.

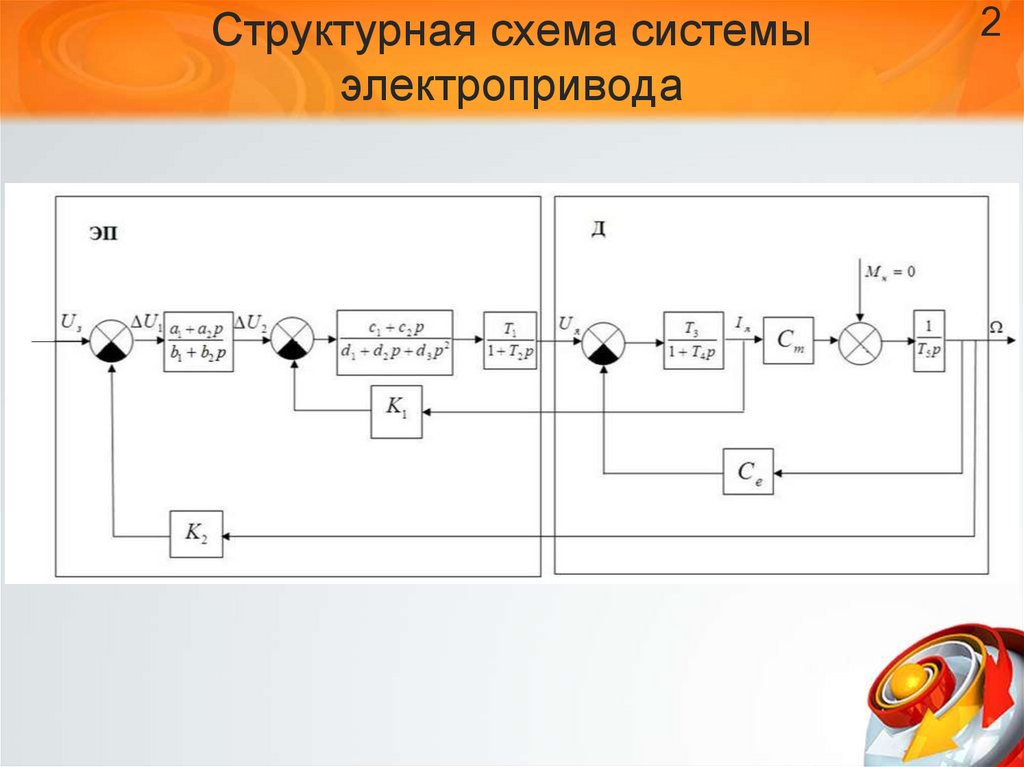
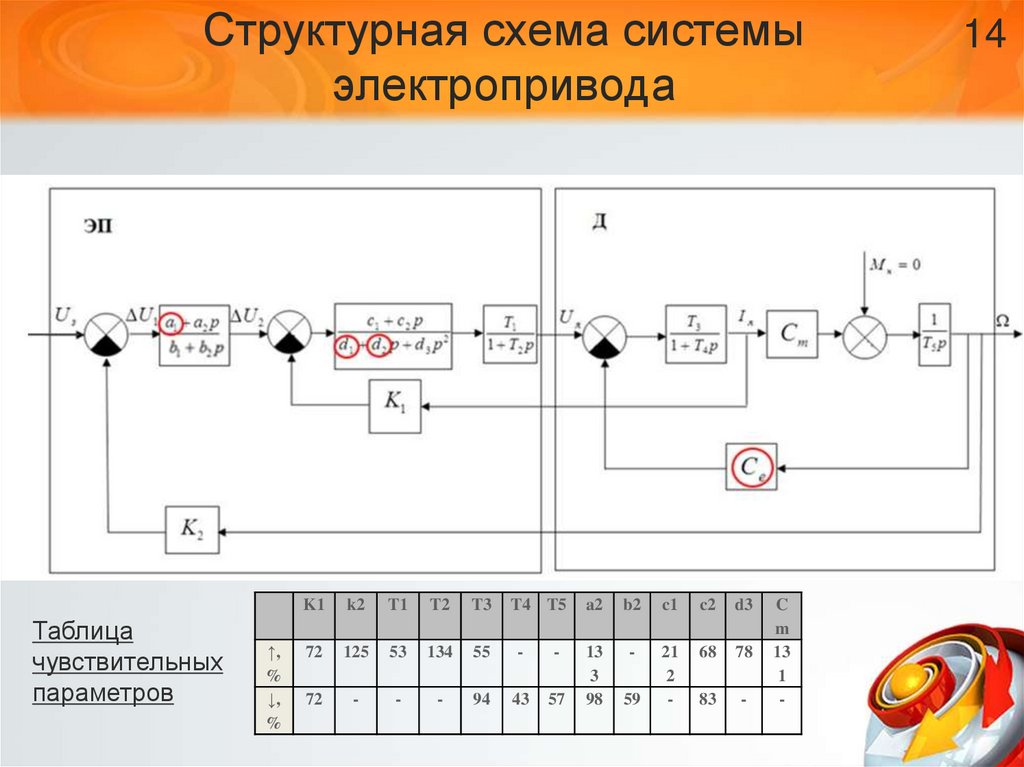
2. Структурная схема системы электропривода

2

3. Передаточные функции отдельных звеньев [4,5]

3
a1 a2 p
Передаточная функция регулятора скорости
b1 b2 p
с1 с2 p Передаточная функция регулятора тока
W2 ( p)
d1 d 2 p d 3 p 2
W1 ( p )
W3 ( p)
T1
1 T2 p
Передаточная функция тиристорного преобразователя
W4 ( p)
T3
1 T4 p
Передаточная функция цепи якоря
1
Передаточная функция двигателя
T5 p
K1, K 2 - коэффициенты усиления в цепях обратной связи контура тока и скорости
W5 ( p )
Cm, CE - коэффициенты усиления по моменту и ЭДС
W 5 (p) – интегрирующее звено
W 3 (p), W4(p) - апериодические звенья

4.

Расчет главной передаточной
функции
U З K 2 W1 ( p) I Я K1 W2 ( p)W3 ( p) U Я
U Я Сe W4 ( p) I Я
U С W ( p) / W ( p)
e
4
5
Я
( p) F ( p)U З ( p)
R2 ( p )
r2 r1 p r0 p 2
F ( p)
Q6 ( p ) q6 q5 p q4 p 2 q3 p 3 q2 p 4 q1 p5 q0 p 6
Характеристическое уравнение:
Q6 ( p ) q0 p 6 q1 p 5 q2 p 4 q3 p 3 q4 p 2 q5 p q6 0
4

5. Разработка программного обеспечения

Алгоритм расчета
1.
Задание параметров, передаточных функций отдельных звеньев и
коэффициентов усиления в цепях обратной связи.
2.
Вычисление главной передаточной функции и характеристического
уравнения.
3.
Определение области устойчивости в плоскостях и пространствах
выбранных параметров.
4.
Анализ устойчивости системы ЭП при вариации различных параметров в
режиме анимации.
5

6. Исследование устойчивости по расположению корней на комплексной плоскости

6
Im
Q6 ( p) q6 q5 p q4 p 2 q3 p 3 q2 p 4 q1 p 5 q0 p 6 0
ближайший к мнимой оси корень
pi i
степень устойчивости, с 1
колебательность переходного процесса,
б/р
Re
d
2
2
логарифмический декремент затухания,
б/р
2
2
d
добротность колебательного контура,
б/р
Q
d 2

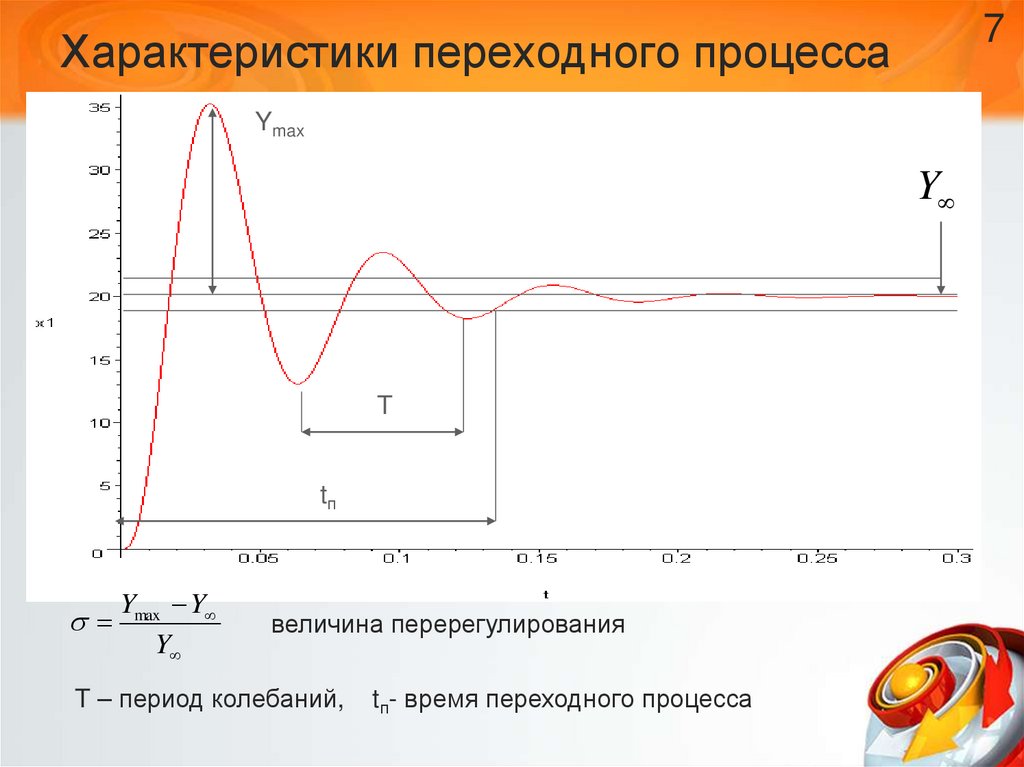
7. Характеристики переходного процесса

7
Характеристики переходного процесса
Ymax
Y
T
tп
Ymax Y
Y
величина перерегулирования
T – период колебаний,
tп- время переходного процесса

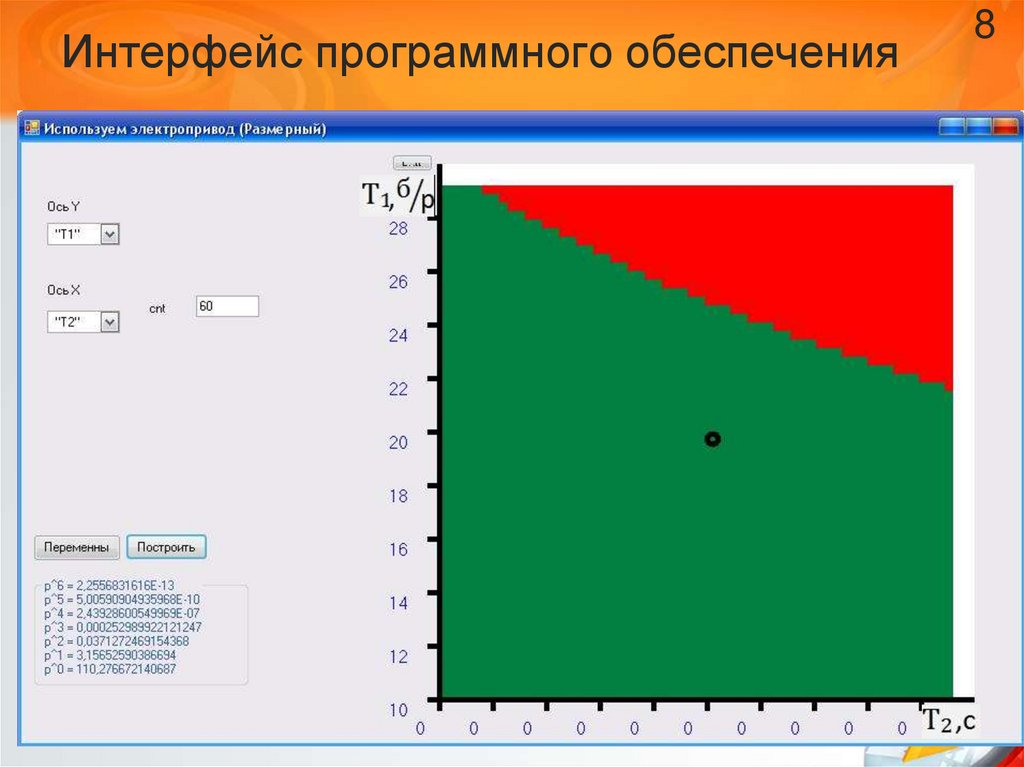
8. Интерфейс программного обеспечения

8

9. Изменение областей устойчивости в плоскости параметров (K1,K2) при изменении Т3

Изменение областей устойчивости в плоскости
9
параметров (K1,K2) при изменении Т3
T3=2.757
T3=2.857
T3=2.957
T3=3.057

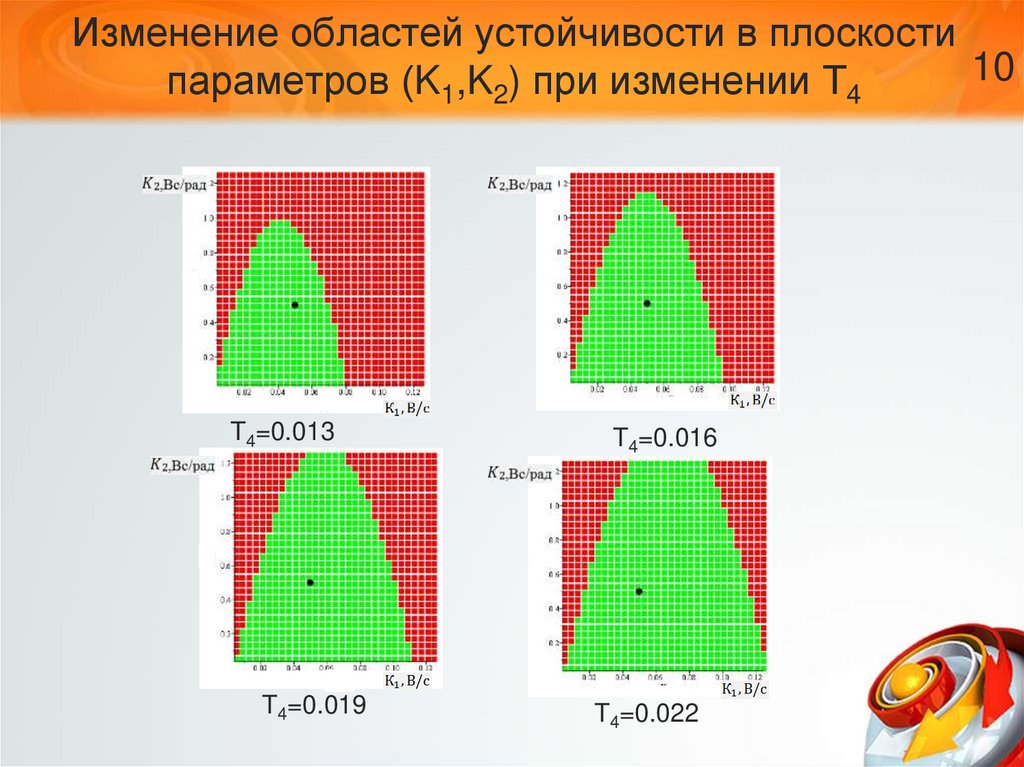
10. Изменение областей устойчивости в плоскости параметров (K1,K2) при изменении Т4

Изменение областей устойчивости в плоскости
10
параметров (K1,K2) при изменении Т4
T4=0.013
T4=0.019
T4=0.016
T4=0.022

11. Область устойчивости в плоскости параметров (a2,b2)

Область устойчивости в плоскости параметров
11
(a2,b2)

12. Область устойчивости в плоскости параметров (а2,К2)

Область устойчивости в плоскости параметров
12
(а2,К2)

13.

Анализ корней характеристического уравнения при
изменении параметров системы в режиме анимации
13

14. Структурная схема системы электропривода

Таблица
чувствительных
параметров
↑,
%
↓,
%
K1
k2
T1
T2
T3
T4 T5
a2
b2
c1
c2
d3
72
125
53
134
55
-
-
-
78
-
-
-
94
43
57
21
2
-
68
72
13
3
98
83
-
59
C
m
13
1
-
14

15. Фрагмент программы анимации

15

16. Список используемой литературы

16
1. Бесекерский В.А., Попов Е.П. Теория систем автоматического
регулирования.
М., Наука, 1966.
2. Айзерман М.А. Теория автоматического регулирования. М, Наука, 1966.
3. Попов Е.П. Теория линейных систем автоматического регулирования и
управления: Учебное пособие для втузов. – 2-е издание переработано и дополнено –
М., Наука. Гл. ред. физ.-мат. лит., 1989.
4. Чиликин М.Г. Основы автоматизированного электропривода. М., Энергия, 1974.
5. Михайлов О.П. Динамика электромеханического привода металлорежущих
станков. М., 1989.
6. Соколов М.М. Автоматизированный электропривод общепромышленных
механизмов. Изд. 3-е, переработ. и доп., М., Энергия, 1976.
7. Горяченко В.Д. Элементы теории колебаний: Учебное пособие. Красноярск, Изд-во
Красноярского университета, 1995.
8. Гололобов Н.Н., Стребуляев С.Н., Кузьмин В.П., Исследование устойчивости и
переходных процессов систем электроприводов подач станков с числовым
программным управлением, в сб. «Труды III Конференции молодых ученых НИИ
прикладной математике и кибернетики и факультета ВМК», Горький, ДЕП, ВИНИТИ,
1983.
9. Прохорова О.С. Определение показателей динамического качества системы
электропривода. Дипломная работа, научный руководитель С.Н. Стребуляев, ННГУ,
2007г.
10. Неймарк Ю.И. Устойчивость линеаризованных систем ЛКВВИА, 1949г.
11. Никитин П. М. Дипломная работа на тему «Исследование робастной устойчивости
динамической модели электропривода», Нижний Новгород, 2011