Задачи повышенного уровня сложности по теории вероятности и математической статистике

1.

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ
РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное
образовательное учреждение высшего образования
«ПЕНЗЕНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»
Задачи повышенного уровня сложности по теории вероятности и
математической статистике
Пенза, 2024 г.

2.

Цель:
•разработать рекомендации по подготовке школьников к
решению задач повышенной сложности по теории
вероятности и математической статистике на олимпиадах.
Проблема:
•школьники, даже обладающие хорошими базовыми
знаниями, испытывают трудности при решении задач
повышенной сложности по теории вероятностей и
статистике на олимпиадах из-за нехватки методической
подготовки, систематического опыта и стратегий решения
нестандартных задач.

3.

Задачи проекта
1
П роанализироват ь и классиф ицироват ь задачи по т еории вероят ност и и
м ат ем ат ической ст ат ист ике повы ш енного уровня слож ност и.
2
В ы явит ь основны е т рудност и, с кот оры м и ст алкиваю т ся ш кольники.
3
Р азработ ат ь реком ендации для эф ф ект ивной подгот овки к олим пиадам по
т еории вероят ност и.
4
Сф орм улироват ь вы воды по ит огам исследования

4.

КЛАССИФИКАЦИЯ ЗАДАЧ
Комбинаторные задачи
• Задачи на подсчет числа исходов.
• Задачи на использование формул
комбинаторики (перестановки,
сочетания, размещения).
Задачи на использование
теорем сложения и
умножения вероятностей
• Задачи на применение теоремы
сложения вероятностей.
• Задачи на применение теоремы
умножения вероятностей.
Задачи на независимые
события и условную
вероятность
• Задачи на проверку
независимости событий.
• Задачи на вычисление условной
вероятности.
Статистические задачи
• Задачи на обработку и анализ
данных.
• Задачи на использование
выборочных характеристик
Классическая вероятность
• Задачи на вычисление
вероятности событий.
• Задачи на использование
формулы полной вероятности и
формулы Байеса.
Геометрическая
вероятность
• Задачи на вычисление
вероятности попадания в область.
• Задачи на использование
геометрических фигур и их
свойств.
Случайные величины и их
распределения
• Задачи на нахождение
математического ожидания и
дисперсии.

5.

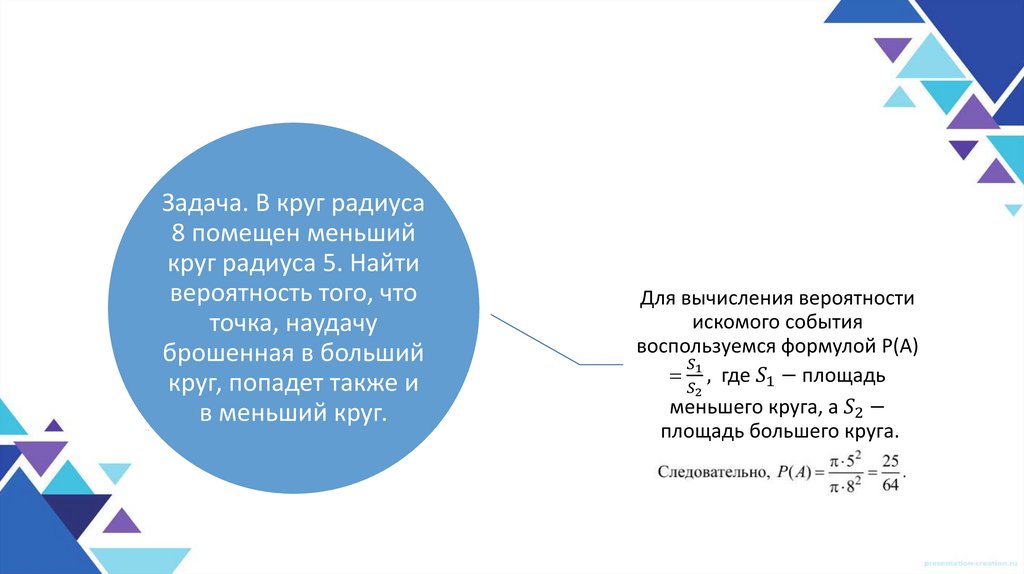
Подбор и адаптация задач по каждому разделу
Задача 1. Из урны, в которой находятся 6 черных шаров и 4 белых шара, вынимают
одновременно 3 шара. Найдите вероятность того, что среди отобранных два шара
будут черными.
• Решение:
• Для вычисления события A (среди отобранных шаров два шара будут черными)
m
воспользуемся формулой P(A) ,где n – общее число возможных
n
элементарных исходов испытания, а m – число элементарных исходов,
благоприятствующих появлению события A. В нашем случае общее число
возможных элементарных исходов равно числу способов, которыми можно
3
извлечь три шара из десяти имеющихся, то есть