Основы теории предельного равновесия (Лекция №8)

1. Л Е К Ц И Я №8 Основы теории предельного равновесия

2. П л а н 8.1 Основные уравнения теории предельного равновесия 8.2 Критические нагрузки на грунты основания 8.3 Анализ

План
8.1 Основные уравнения теории предельного
равновесия
8.2 Критические нагрузки на грунты основания
8.3 Анализ устойчивости сооружения

3.

8.1 Основные уравнения предельного равновесия
Предельным равновесием основания называют
такое напряженное состояние, при котором
незначительное увеличение внешней нагрузки
приведет к нарушению установившегося равновесия и вызовет потерю устойчивости грунта,
сопровождающееся выпором грунта из под
подошвы фундамента сооружения со значительным нарастанием осадки.

4.

В зависимости от величины внешней нагрузки
на грунт различают два понятия:
- допредельное состояние характеризуется
деформациями, изменение которых может произойти
из-за повышения уровня напряжений или в результате
временных эффектов.
- предельное состояние характеризуется
достижением напряжениями такой критической
комбинации, при которой устанавливается предельное равновесие между внешней нагрузкой и
внутренними силами сопротивления грунта.

5.

Для изучения прочности грунта в условиях
сложного напряженного состояния применяют
два основных условия (теории)
- условие Мора-Кулона;
- условие Мизеса-Шлейхера.

6.

Теория Кулона Мора
Для несвязных грунтов
Для связных грунтов
= tg
= tg +c
(1)
(2)
1 2 3
Положение площадки скольжения (а) и напряжения
на наклонной площадке(б)

7.

Нормальное напряжение по наклонной площадке.
1
1
( 1 3 ) ( 1 3 ) sin 2
2
2
(3)
Касательное напряжение по наклонной площадке.
1
( 1 3 )соs 2
2
(4)
Напряжения в предельном состоянии
= tg +c
(5)

8.

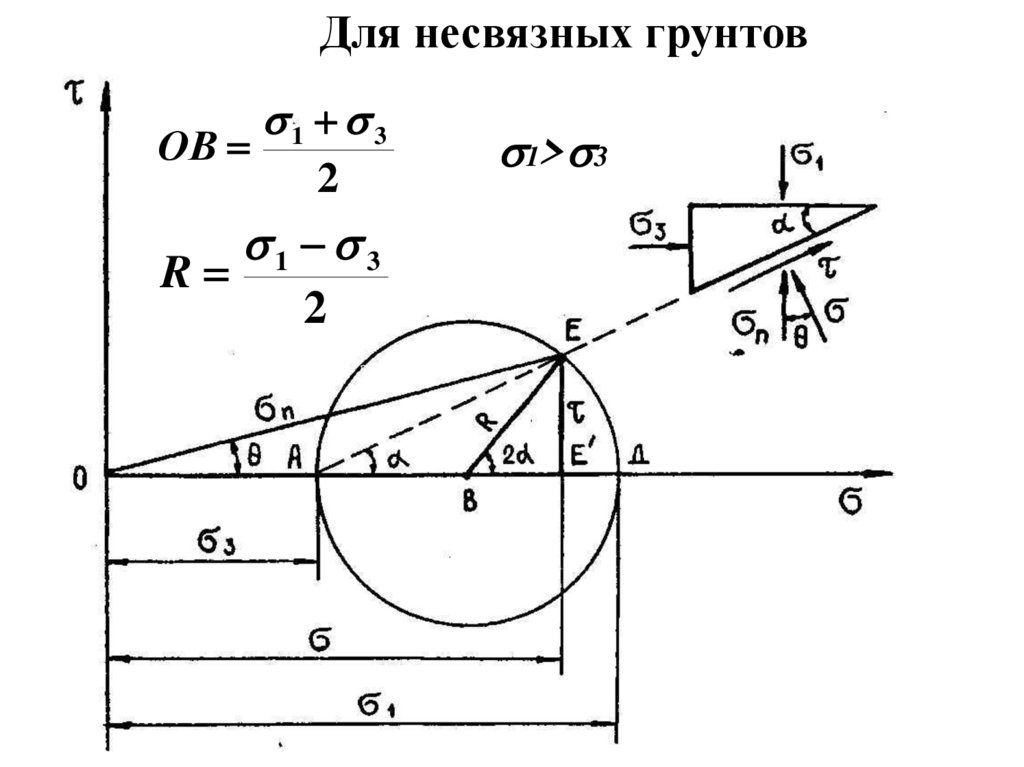
Для несвязных грунтов
ОВ
R
1 3
2
1 3
2
1> 3

9.

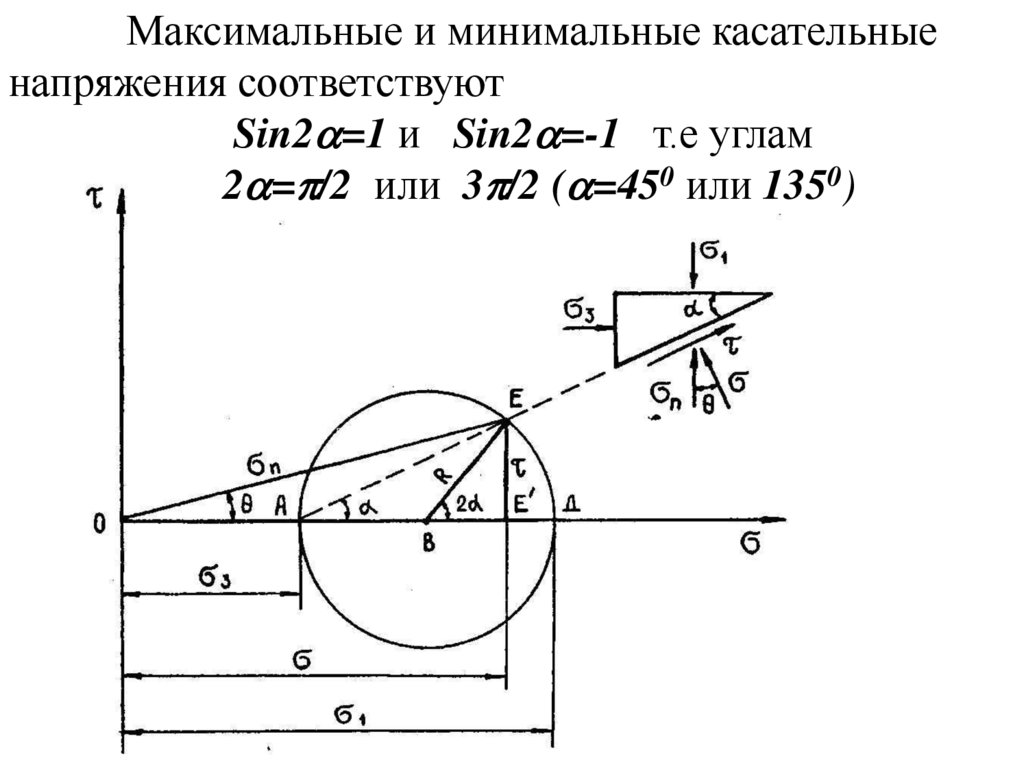
Максимальные и минимальные касательные
напряжения соответствуют
Sin2 =1 и Sin2 =-1 т.е углам
2 = /2 или 3 /2 ( =450 или 1350)

10.

Полное результирующее напряжение на рассматриваемой площадке
2
2
п
Угол отклонения от
нормали к площадке
п arctg
(6)

11.

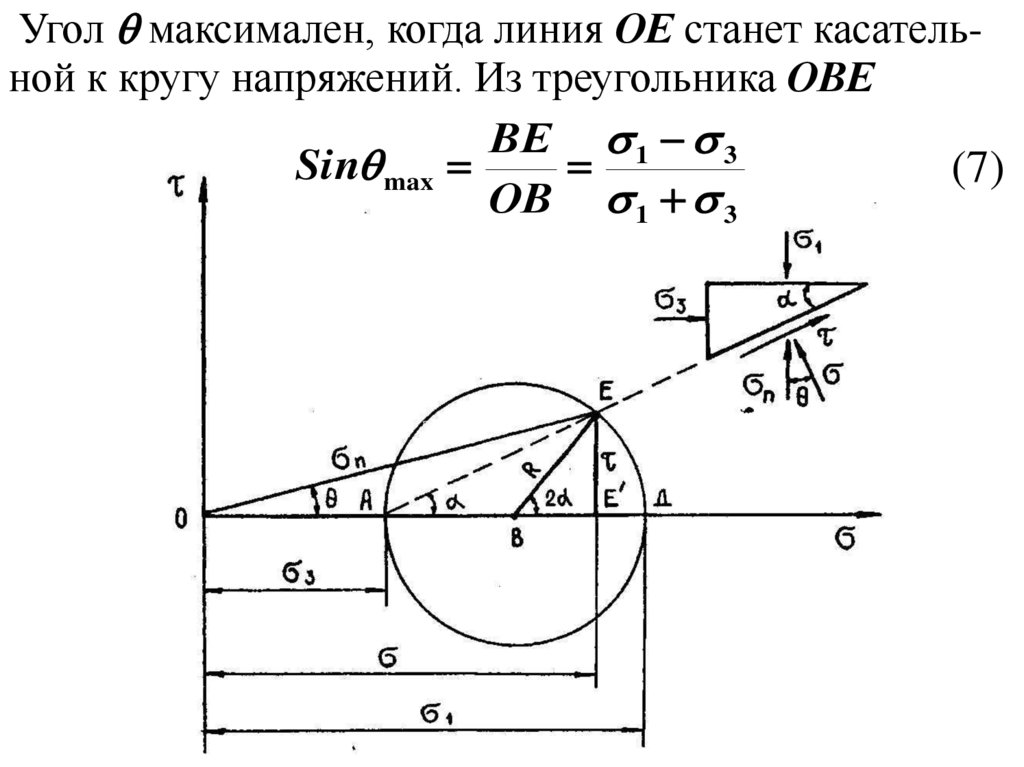
Угол максимален, когда линия ОЕ станет касательной к кругу напряжений. Из треугольника ОВЕ
ВЕ 1 3
Sin max
(7)
ОВ 1 3

12.

Максимальное отклонение полного (результирующего) напряжения на угол max от нормали к площадке
имеет место при
1
1 - 3
max 1
max
аrcsin
(8)
2 2
2
4 2
1 3
4
Следовательно, отклонения площадки скольжения
от направления наибольшего главного напряжения 1
45
0
2
(9)

13.

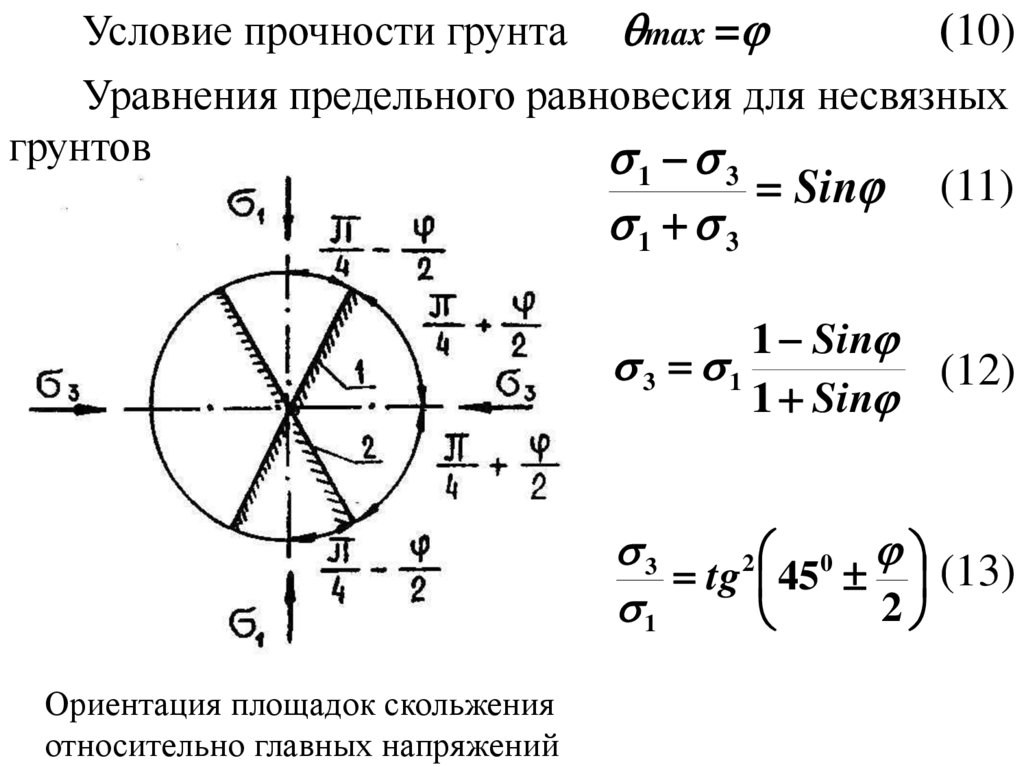
Условие прочности грунта max =
(10)
Уравнения предельного равновесия для несвязных
грунтов
1
3
1 3
Sin
(11)
1 Sin
3 1
(12)
1 Sin
3
(13)
2
0
tg 45
1
2
Ориентация площадок скольжения
относительно главных напряжений

14.

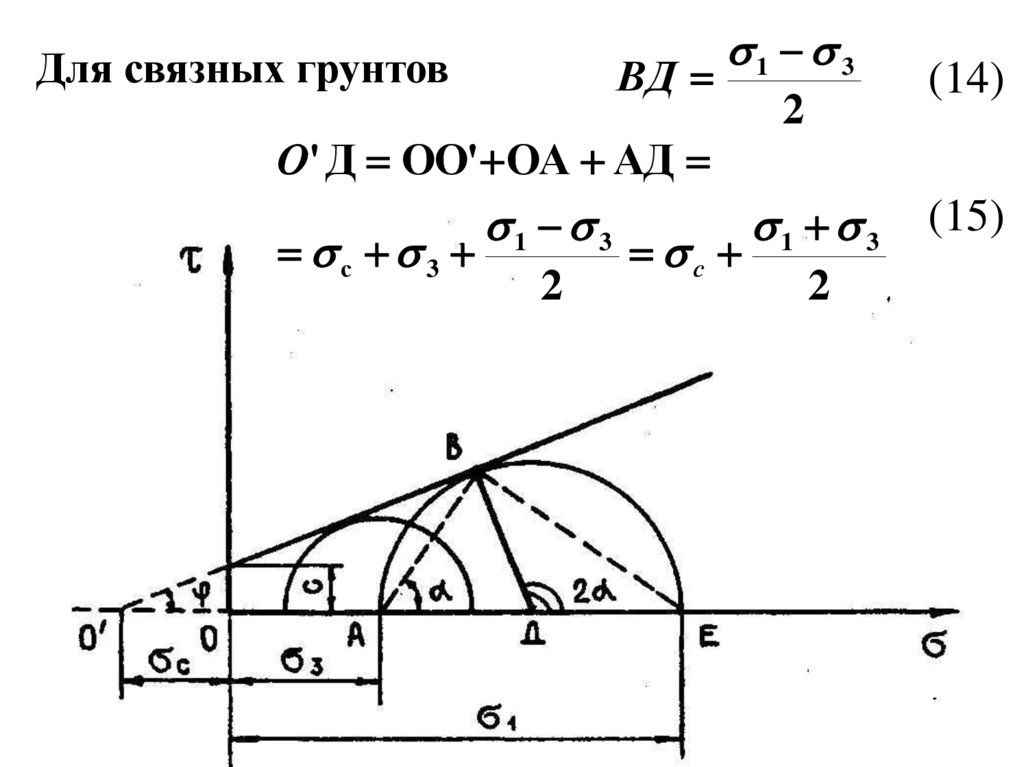
Для связных грунтов
ВД
1 3
2
О' Д ОО' ОА АД
1 3
1 3
с 3
с
2
2
(14)
(15)

15.

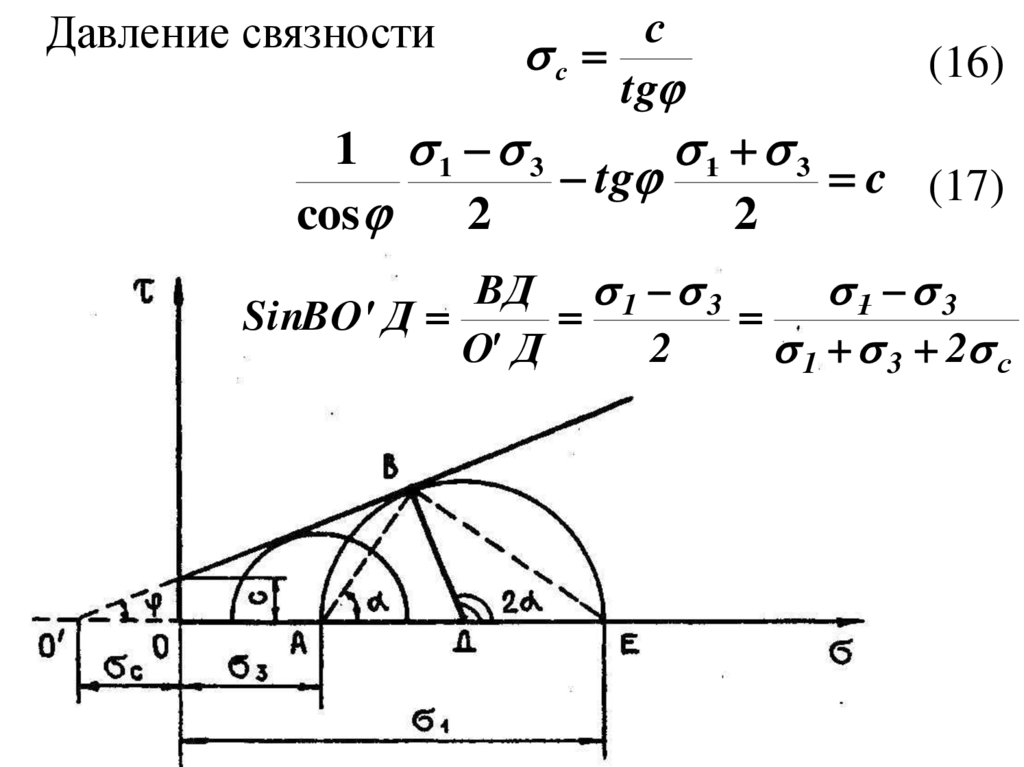
Давление связности
с
с
tg
(16)
1 1 3
1 3
tg
c (17)
cos
2
2
ВД 1 3
1 3
SinВО' Д
О' Д
2
1 3 2 с

16.

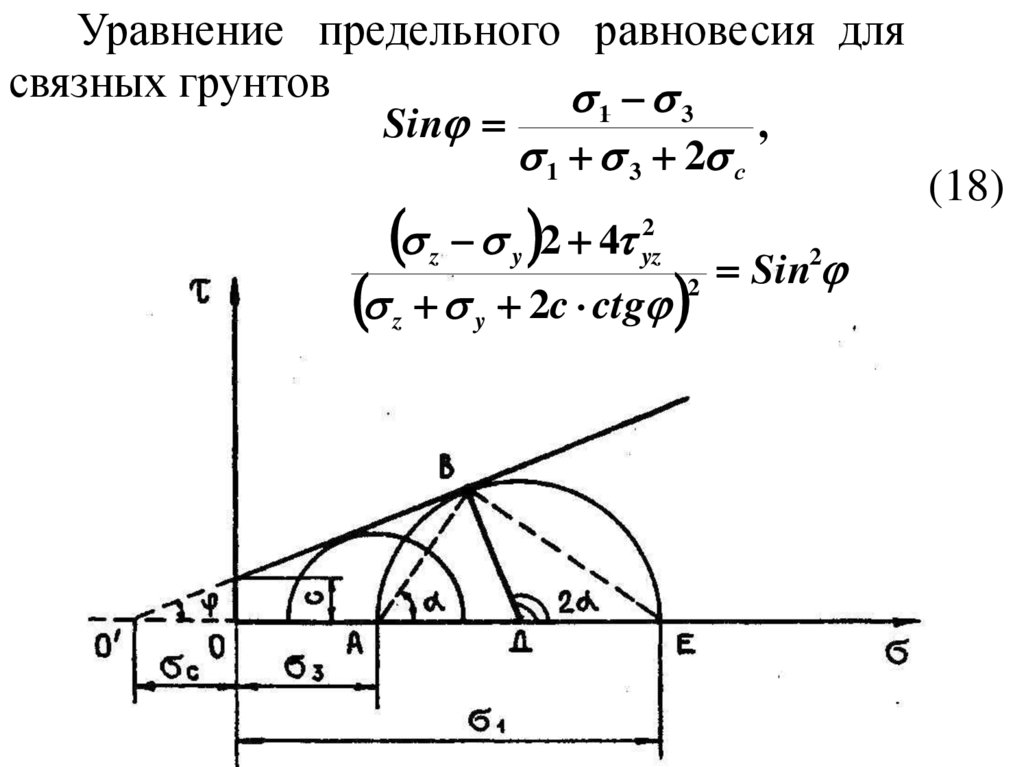
Уравнение предельного равновесия для
связных грунтов
1 3
Sin
,
1 3 2 с
2 4
z
y
2
yz
2
Sin
2
2c ctg
z
y
(18)

17.

Плоская задача. Уравнения равновесия в
дифференциальной форме при плоской задаче
d y d yz
0
dy
dz
d z d yz
dz
dy
(19)
Уравнение предельного равновесия выраженное
через компоненты напряжений, соответствующие
координатным осям
z y 4 yz
2
sin
2
z y 2c ctg
2
(19’)

18.

Пространственная задача имеет замкнутую
систему уравнений (статически определимую)
только для случая осевой симметрии
d r d rz r
0
dr
dz
r
d z d rz rz
0
dz
dr
r
4
2
y
z
2
yz
2c ctg
2
y
z
(20)
sin
2

19.

8.2 Критические нагрузки на грунты основания
Предельное напряженное состояние грунта под
полосовой нагрузкой. Задача Пузыревского.
Основные гипотезы:
- компоненты напряжений распределяются в грунтовом массиве, в соответствии с решением Фламана для
плоской задачи;
- коэффициент бокового давления грунта в предельном состоянии равен единице.

20.

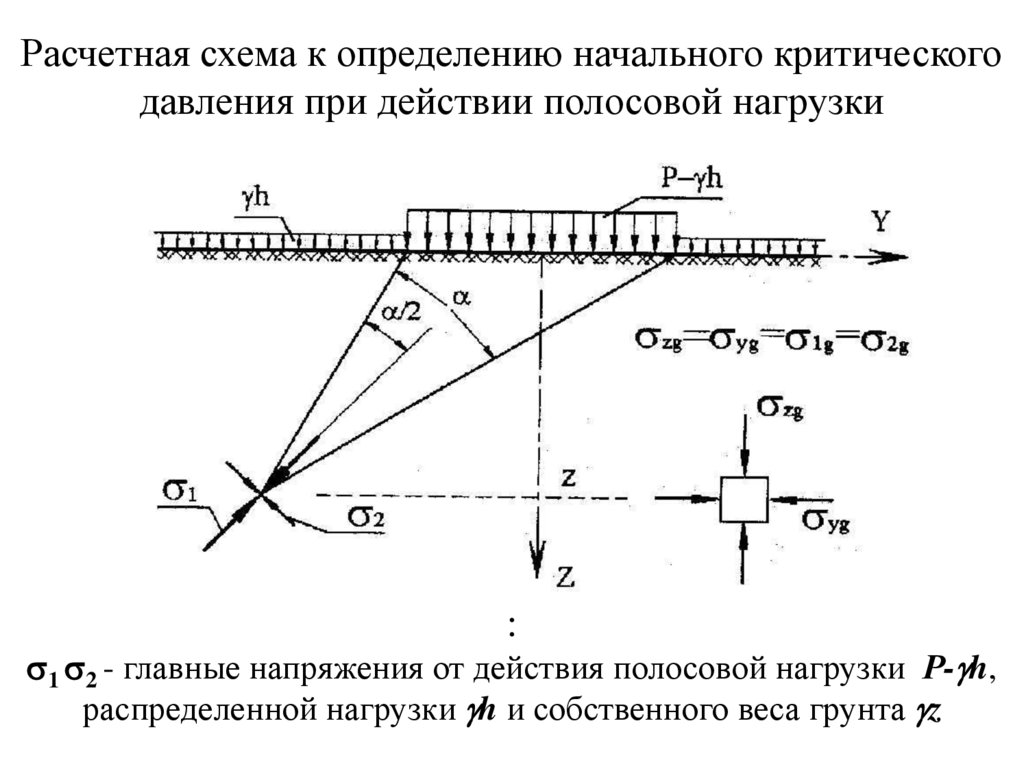
Расчетная схема к определению начального критического
давления при действии полосовой нагрузки
:
1 2 - главные напряжения от действия полосовой нагрузки Р- h,
распределенной нагрузки h и собственного веса грунта z

21.

Р h
1
3
( sin ) ( h z )
Р h
(21)
( sin ) ( h z )
Условие предельного равновесия примем в форме
закона Кулона-Мора для главных напряжений
1 3
sin
1 3 2 с сtg
(22)

22.

Уравнение предельного равновесия весомого грунта
под полосовой нагрузкой с учетом пригруза на поверхности
( h z с сtg )
р
h
sin
sin
(23)
Значение координаты соответствующее максимальному значению знаменателя, определяется из
уравнения:
d sin
cos
0
1 0
d sin
sin
сos =sin
= /2 -
sin =сos
(24)

23.

Критическое значение полосовой нагрузки, соответствующее развитию зон пластического деформирования на глубину z.
р
ctg
2
( z h c ctg ) h
(25)
Начальным критическим давлением на
основание называется то значение давления, при
котором в грунте основания возникают области
предельного напряженного состояния

24.

Формула Пузыревского для равномерно распределенной
нагрузке по полосе в условиях плоской деформации
нач
кр
р
ctg
( h c ctg ) h
(26)
2
где – объемный вес грунта;
h- глубина заложения фундамента;
- угол внутреннего трения грунта;
с - удельное сцепление грунта
Расчетное сопротивление грунта – это критическое
давление, при котором зоны пластического деформирования распространяются на глубину 0,25b (b-ширина фундамента).

25.

Выражение (26) можно привести к виду:
Pнач.кр = M b + Mq ' h + Mc c
(27)
Коэффициенты, определяемые по таблице
M
0, 25
ctg
Mq
2
Mc
ctg
ctg
ctg
2
1
2
(28)

26.

При расчете оснований по деформациям необходимо,
чтобы удовлетворялось условие
Р R
(29)
где Р- среднее давление по подошве фундамента;
R- расчетное сопротивление грунта основания.
.
Расчетное сопротивление грунта основания
'
с1 с 2 M kb II M q ( d1 db) II
R
'
k
db II M c c II
(30)

27.

где с1 и с2 - коэффициенты условий работы, соответственно основания и сооружения во взаимодействии с основанием;
k- коэффициент, принимаемый k=1 – если прочностные характеристики грунта определены непосредственными испытаниями и k=1,1 – если они
приняты по таблицам СНиП;
kz- коэффициент, принимаемый kz=1 при b<10м;
kz=z0/b+0,2 при k 10 м (здесь z0=8 м);
b- ширина подошвы фундамента, м;

28.

II и ’II – усредненные расчетные значения
удельного веса грунтов, залегающих соответственно
ниже подошвы фундамента (при наличии подземных
вод определяется с учетом взвешивающего действия
воды) и выше подошвы, кН/м3;
db- глубина подвала –расстояние от уровня
планировки до пола подвала, м (для сооружений с
подвалом шириной B 20 и принимается db=0);
М , Мg, Мc- коэффициенты, зависящие от расчетного значения угла внутреннего трения принимаемые по таблице СНиП 2.02.01-83";

29.

d1- глубина заложения фундамента от пола до подвала; при отсутствии пола подвала - от планировочной
отметки, м;
cf
d1 hs hsf '
II
где
hs- толщина слоя грунта выше подошвы
фундамента со стороны подвала, м;
hsf- толщина конструкции пола подвала, м;
cf- расчетное значение удельного веса
конструкции пола подвала, кН/м3.

30.

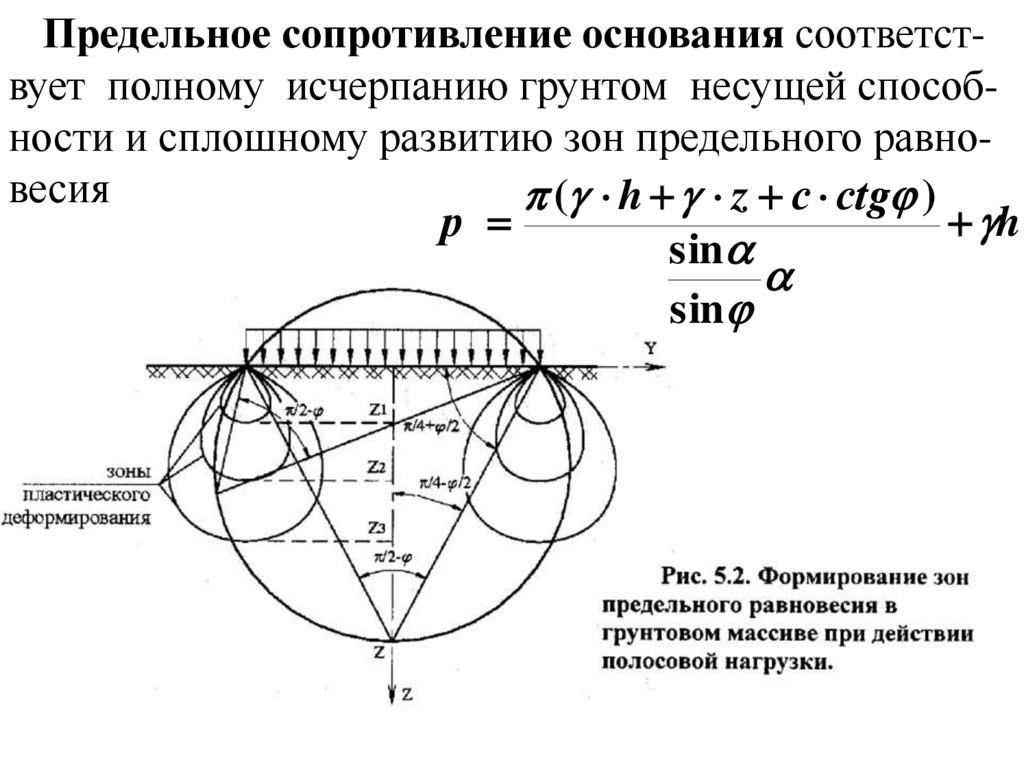
Предельное сопротивление основания соответствует полному исчерпанию грунтом несущей способности и сплошному развитию зон предельного равновесия
( h z с сtg )
р
h
sin
sin

31.

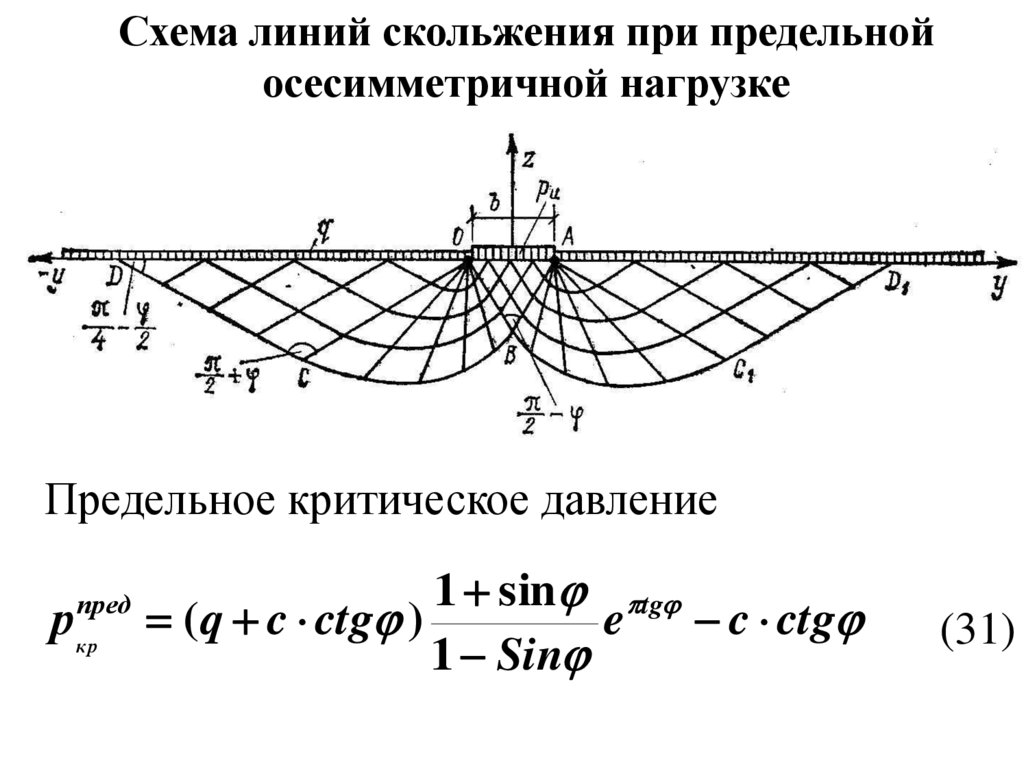
Схема линий скольжения при предельной
осесимметричной нагрузке
Предельное критическое давление
пред
ркр
1 sin tg
( q c ctg )
e c ctg
1 Sin
(31)

32.

Для плоской задачи принята следующая схема
линий скольжения и получена формула
(29)
пред
п
р
N y. n b Nq. n ' h Nc . nc (32)

33.

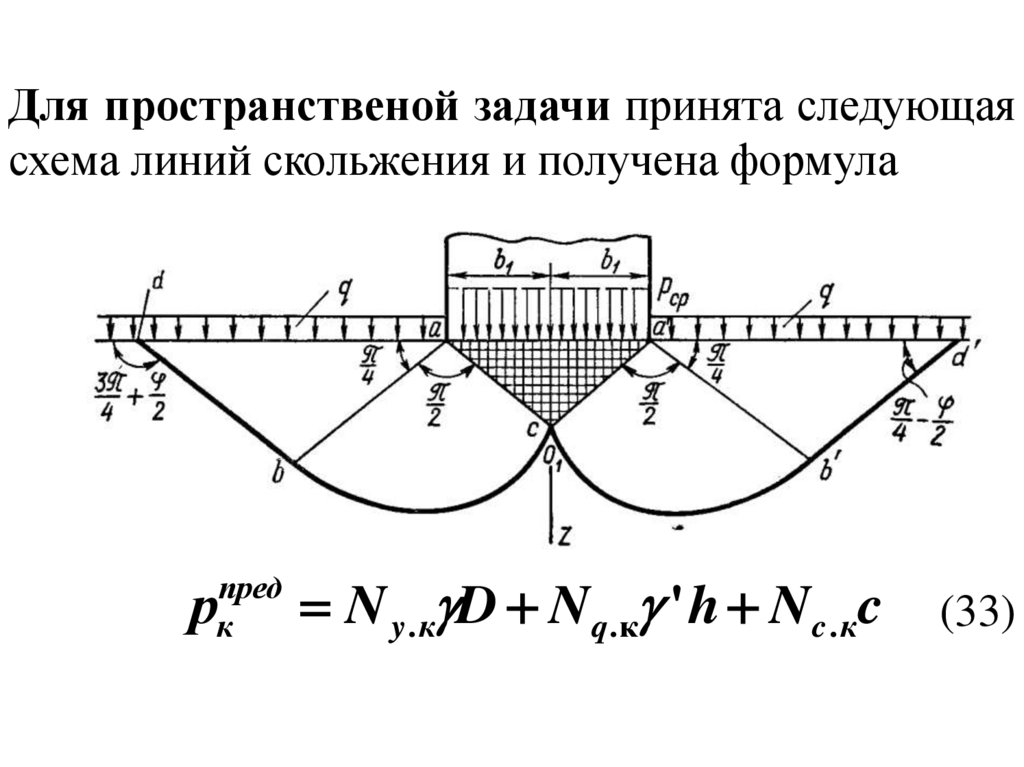
Для пространственой задачи принята следующая
схема линий скольжения и получена формула
пред
к
р
N y. к D Nq.к ' h Nc . к c
(33)

34.

где N - с соответствующими индексами – безразмерные коэффициенты несущей способности, которые
принимаются по таблицам в зависимости от угла
внутреннего трения, ;
b- ширина ленточного фундамента;
D- диаметр круглого фундамента;
и ' - средний удельный вес грунта соответственно
ниже и выше подошвы фундамента;
h- глубина заложения подошвы фундамента;
с- удельное сцепление

35.

8.3 Анализ устойчивости сооружения
Основой обеспечения устойчивости сооружения,
системы «сооружение – основание» является условие
c
lc F R
n
где
(34)
lc - коэффициент сочетания нагрузок;
F и R – расчетные значения соответственно сдвиговых сил и
сил предельного сопротивления или моментов сил,
стремящихся повернуть и удержать сооружение;
c – коэффициент условий работы;
п– коэффициент надежности по степени ответственности
сооружений.

36.

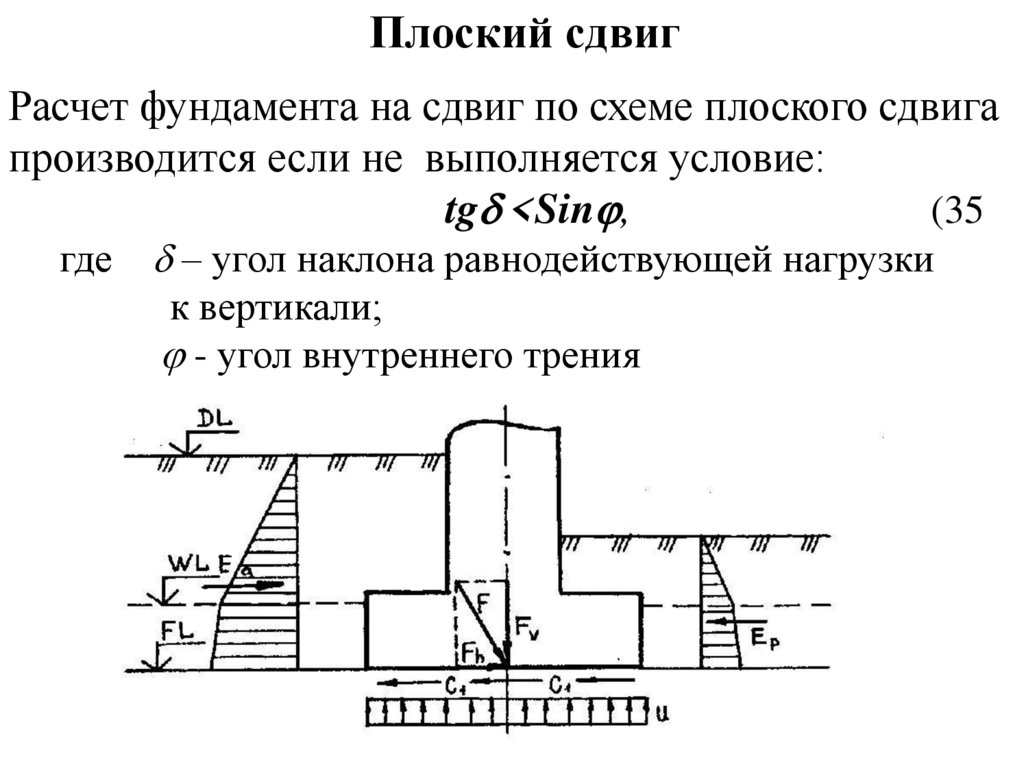
Плоский сдвиг
Расчет фундамента на сдвиг по схеме плоского сдвига
производится если не выполняется условие:
tg <Sin ,
(35
где – угол наклона равнодействующей нагрузки
к вертикали;
- угол внутреннего трения

37.

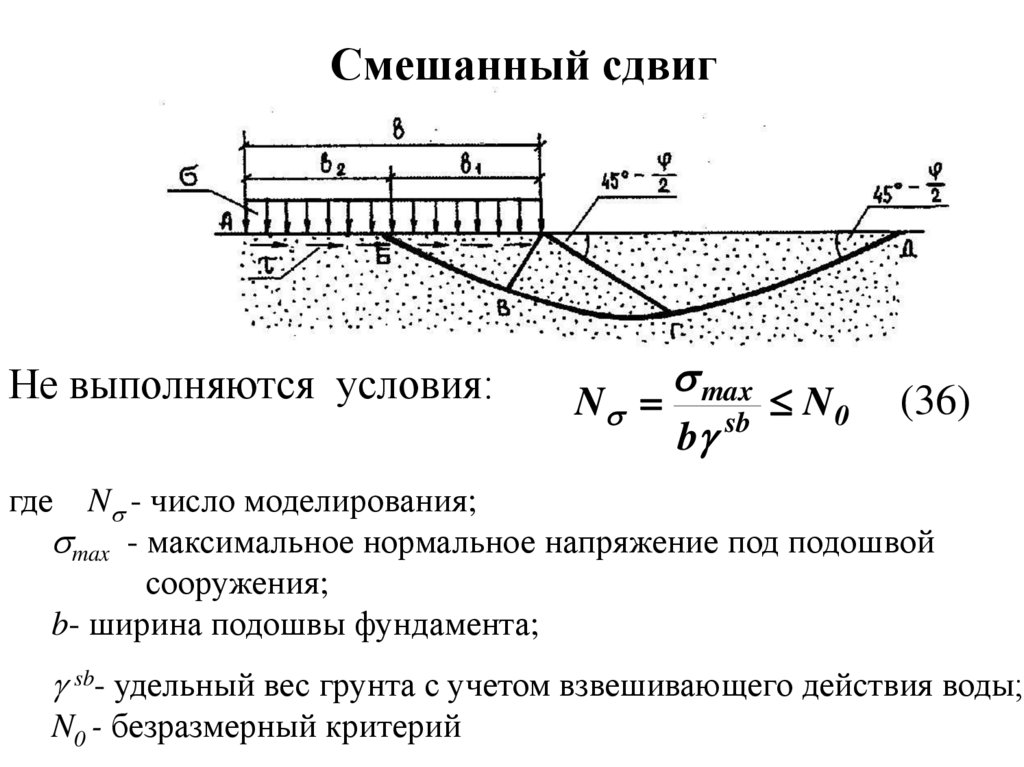
Смешанный сдвиг
Не выполняются условия:
max
N
N0
sb
b
(36)
где N - число моделирования;
max - максимальное нормальное напряжение под подошвой
сооружения;
b- ширина подошвы фундамента;
sb- удельный вес грунта с учетом взвешивающего действия воды;
N0 - безразмерный критерий

38.

k f ( 1 e )t
0
cv
4
2
m0 w h0
tg tg
где
c
m
0 ,45
(37)
(38)
tg - расчетное значение коэффициента сдвига;
m - среднее напряжение по подошве сооружений;
c0v - коэффициент степени консолидации;
t - продолжительность возведения сооружения;
m0 - коэффициент сжимаемости грунта;
w - удельный вес воды;
h0 - расчетная толщина консолидируемая слоя.

39.

Глубинный сдвиг