Механика грунтов, основания и фундаменты

1. МЕХАНИКА ГРУНТОВ, ОСНОВАНИЯ И ФУНДАМЕНТЫ

Преподаватель: доцент кафедры
«Геотехника, тоннели и метрополитены»
БЕССОНОВ ВИТАЛИЙ ВИКТОРОВИЧ

2. Тема 4 Теория устойчивости. Теория предельного равновесия грунтов (ТПРГ)

2

3. Основные задачи теории устойчивости

3
Основные задачи теории устойчивости
Основной предмет исследований
теории устойчивости – процесс
разрушения грунта.
Задачи:
-определение несущей способности
основания;
-определение предельных давлений
грунта на ограждающие конструкции
- оценка устойчивости откосов и
склонов

4. Определение несущей способности основания

4

5. Задача о несущей способности основания

5
Задача о несущей способности
основания
P
u
f =0
f =0
v
f <0
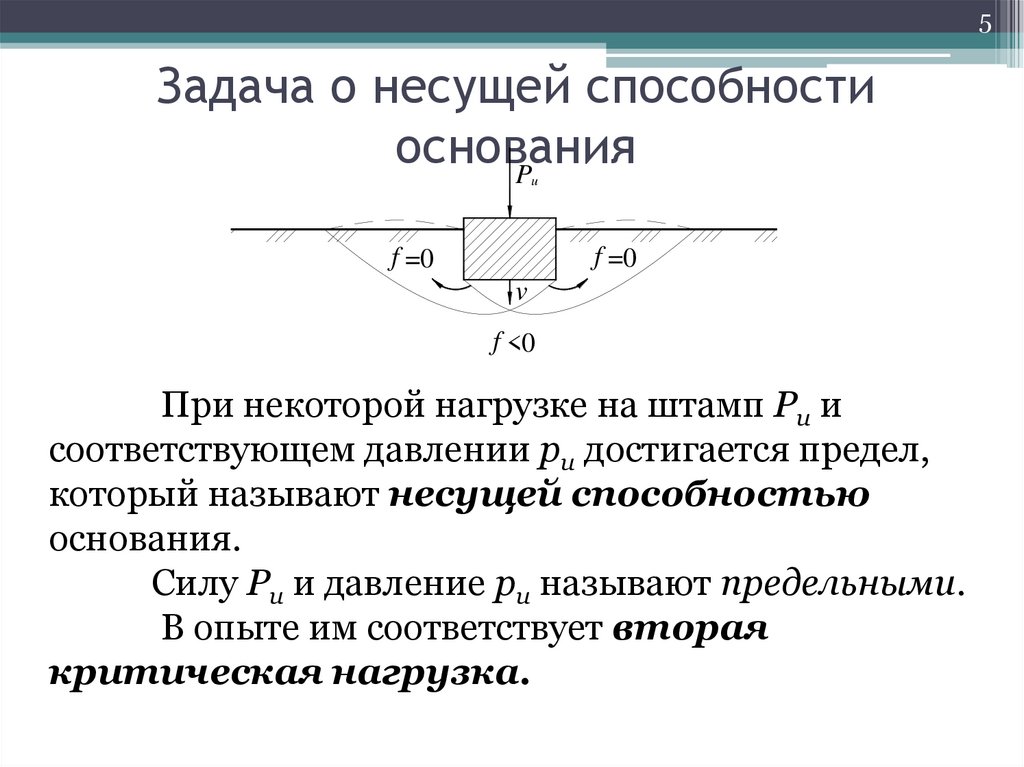
При некоторой нагрузке на штамп Pu и
соответствующем давлении pu достигается предел,
который называют несущей способностью
основания.
Силу Pu и давление pu называют предельными.
В опыте им соответствует вторая
критическая нагрузка.

6. Задача о несущей способности основания

6
Задача о несущей способности
основания
Pu
f =0
f =0
v
f <0
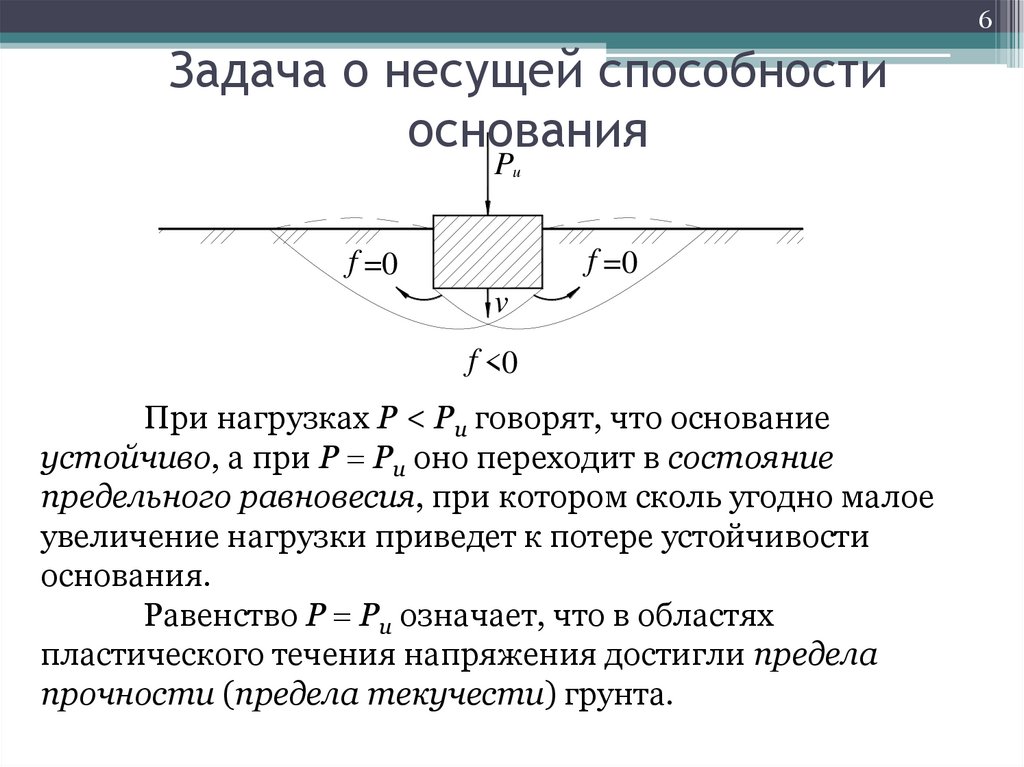
При нагрузках P < Pu говорят, что основание
устойчиво, а при P Pu оно переходит в состояние
предельного равновесия, при котором сколь угодно малое
увеличение нагрузки приведет к потере устойчивости
основания.
Равенство P Pu означает, что в областях
пластического течения напряжения достигли предела
прочности (предела текучести) грунта.

7. Задача о несущей способности основания

7
Задача о несущей способности
основания
Задача о несущей способности
заключается в определении предельной
нагрузки на основание и решается
методами ТПРГ:
Pu f ( , c, , b, d )
где , c и прочностные
характеристики и удельный вес грунта, b
и d ширина штампа (фундамента) и
глубина его заложения.

8.

8
Основные гипотезы плоской задачи
ТПРГ
1. Основание находится в равновесии
2.Каждая точка грунта в
рассматриваемой области находится в
предельном напряженном состоянии,
т.е. напряжения отвечают закону
Кулона Мора.
3.Деформации грунта не
рассматриваются
4.Грунт считается однородным и
изотропным

9. Несущая способность оснований (задача Прандтля, 1920 г.). Предельное давление на невесомое основание.

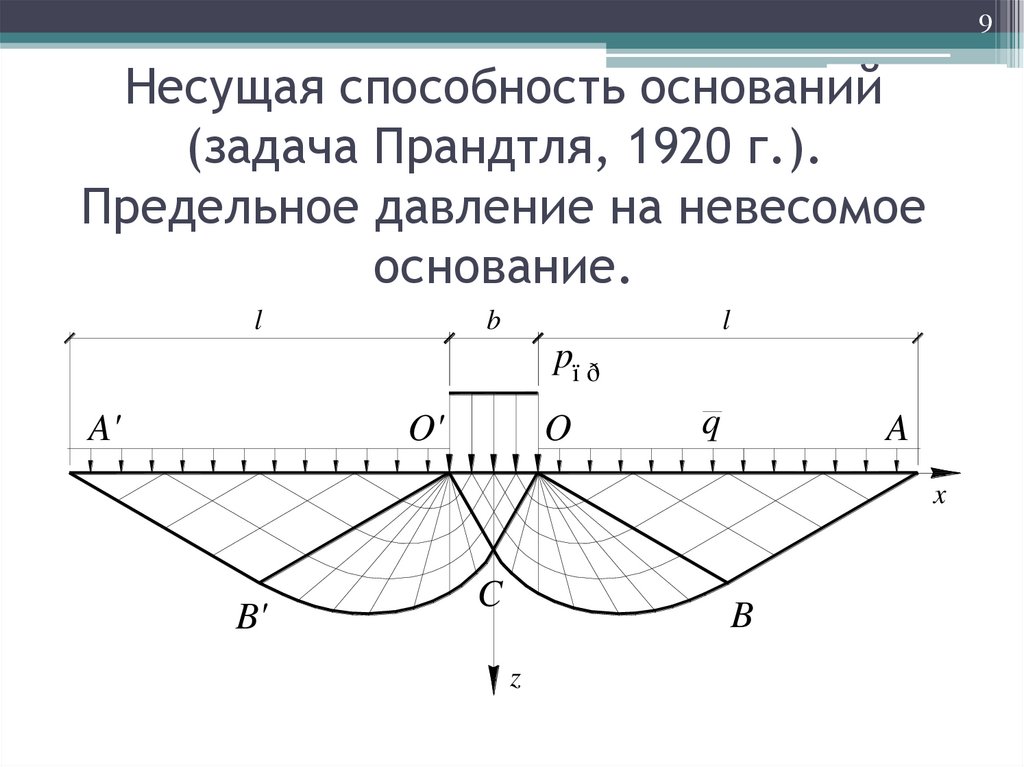
9
Несущая способность оснований
(задача Прандтля, 1920 г.).
Предельное давление на невесомое
основание.
l
b
l
pï ð
A'
O
O'
q
A
x
B'
C
B
z

10.

10
Формула для предельного давления штампа
(фундамента) на невесомое основание (формула
Прандтля):
или
1 sin tg
pu ( q c ctg )
e
c ctg
1 sin
pu N q q N c c
где Nq, Nс - коэффициенты несущей
способности, зависящие от :
Nq
1 sin tg
e
,
1 sin
1 sin tg
Nc
e
1 ctg ( N q 1)ctg
1 sin

11.

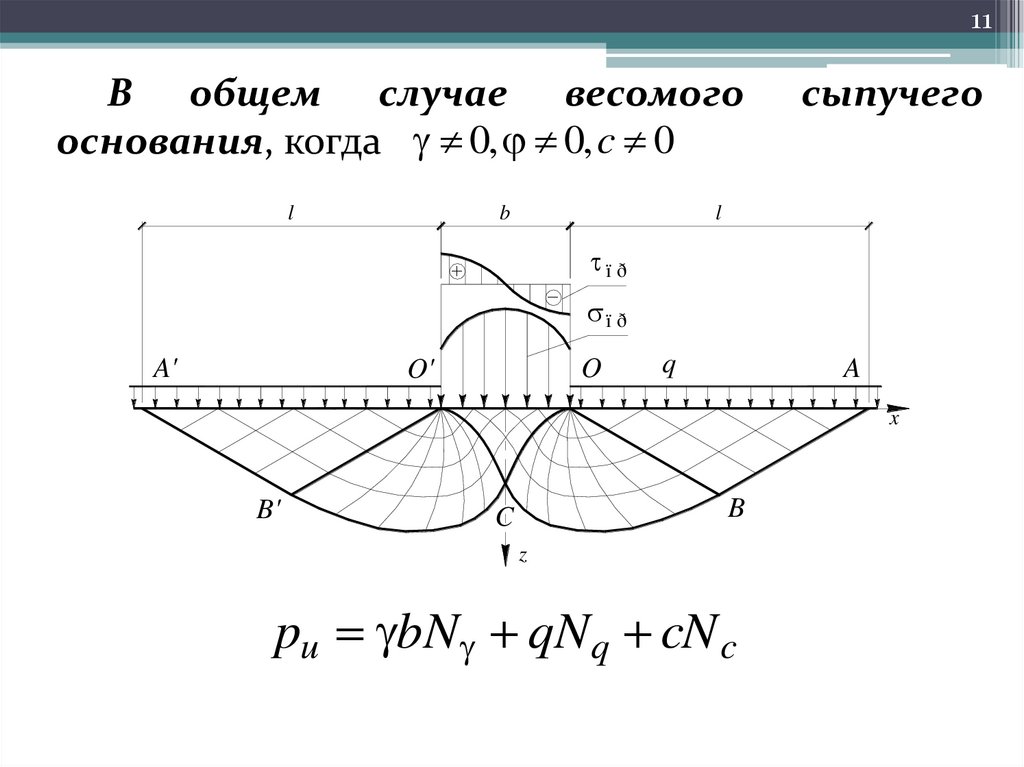
11
В общем случае весомого
основания, когда 0, 0, c 0
l
b
l
ï ð
A'
сыпучего
ï ð
O
O'
q
A
x
B'
B
C
z
pu bN qNq cN c

12. Задача о предельном давлении грунта на ограждающие сооружения

12

13. Давление на ограждающие сооружения

13
Давление на ограждающие
сооружения
В строительной практике часто прибегают
к устройству различных ограждающих
подпорных сооружений

14.

14

15. Давление на ограждающие сооружения

15
Давление на ограждающие сооружения
f =0
Ea
f <0
Ep
À
f =0
f <0
За стенкой образуется призма обрушения, а перед
стенкой призма выпора грунта, в пределах которых грунт
находится в предельном напряженном состоянии.
Со стороны призмы обрушения на стенку действует
сила активного давления грунта Ea, со стороны призмы
выпора сила пассивного давления Ep:
Ea
f ( , c, , h, )
Ep

16. Активное давление грунта

16
Активное давление грунта
Активным называют предельное
давление грунта на стенку,
образующееся при отодвигании стенки
от грунта и обрушении грунта в
сторону стенки. Другое определение:
активное давление это
минимальное давление грунта на
стенку, при котором произойдет
обрушение грунта в сторону стенки.

17. Активное давление

17
Активное давление
Определим величину активного давления
p
z
z p
1
3
a
Для общности предположим, что сверху действует нагрузка p.
На глубине z главные напряжения равны:
1 z p,
3 a

18. Активное давление

18
Активное давление
Подставим эти значения в закон Кулона Мора,
имеем
1 3 ( 1 2 2c ctg ) sin
z p a ( z p a ) sin 2c cos
a (1 sin ) ( z p)(1 sin ) 2c cos
Тогда выражение для
примет вид:
активного давления
1 sin
cos
a ( z p)
2c
1 sin
1 sin

19. Активное давление

19
Активное давление
1 sin
cos
2
tg ;
tg
1 sin
4 2 1 sin
4 2
a ( z p) tg 2c tg ( z p) a 2c a
4 2
4 2
2
где a
1 sin
2
tg
4
2 1 sin
коэффициент активного давления
грунта

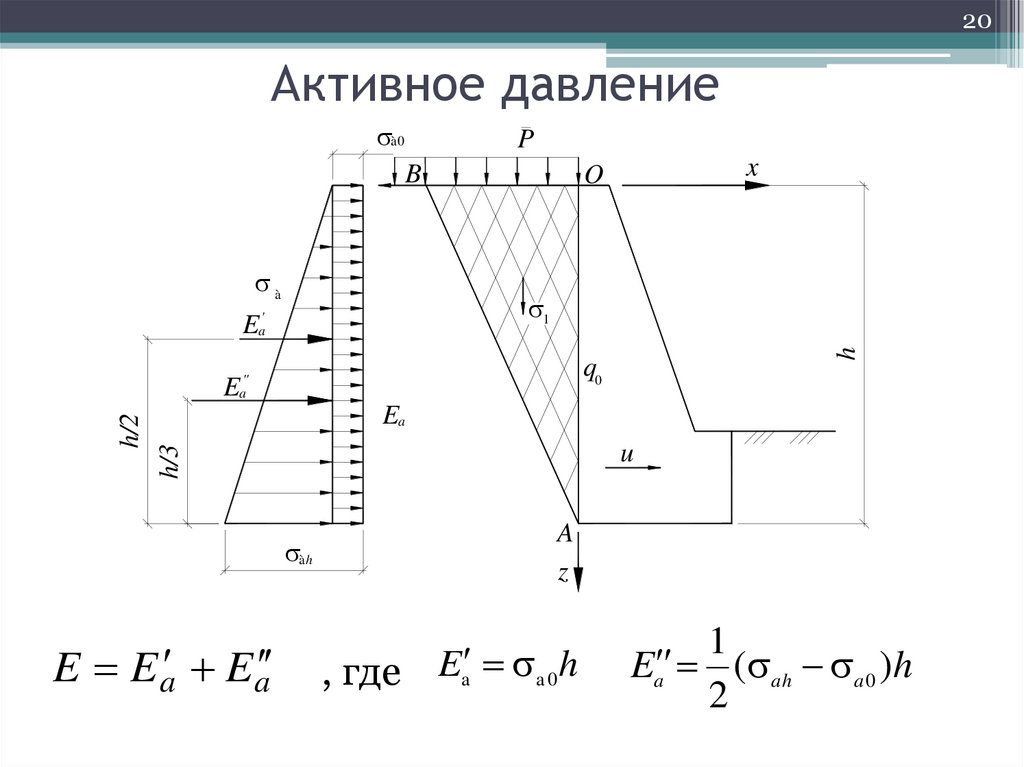
20. Активное давление

20
Активное давление
à0
P
B
à
h
1
Ea'
q0
Ea''
h/2
h/3
Ea
u
àh
E E a E a
x
O
A
z
, где Ea a 0 h
1
Ea ( ah a 0 )h
2

21. Пассивное давление грунта

21
Пассивное давление
грунта
Пассивным называют
предельное давление грунта на
стенку, образующееся при
надвигании стенки на грунт. Другое
определение: пассивное давление
это минимальное давление грунта
на стенку, при котором произойдет
выпор грунта от стенки.

22. Пассивное давление

22
Пассивное давление
q
z
z q
3
1
p
Для общности предположим, что сверху действует
нагрузка q. На глубине z главные напряжения равны:
1 p ,
3 z q

23. Пассивное давление

23
Пассивное давление
Подставим эти значения в закон Кулона Мора,
имеем
p ( z q) ( p z q) sin 2c cos
p (1 sin ) ( z q)(1 sin ) 2c cos
Окончательно выражение
давления примет вид:
для
пассивного
1 sin φ
cosφ
p ( z q)
2c
1 sin
1 sin φ

24. Пассивное давление

24
Пассивное давление
1 sin
cos
2
tg ;
tg
1 sin
4 2 1 sin
4 2
p ( z q) tg 2c tg ( z q) p 2c p
4 2
4 2
2
где
p
1 sin
2
tg
4
2 1 sin
коэффициент пассивного давления
грунта

25. Пассивное давление

25
Пассивное давление
q
p0
O
A x
Pp
'
E
p
''
Ep
ph
E E p E p
z
B
E p p 0 h
1
E p ( ph p 0 )h
2

26. Расчёт устойчивости подпорной стенки

При достаточно большом активном давлении
грунта может произойти потеря устойчивости стенки
либо в форме сдвига, либо в форме опрокидывания
относительно ребра A
Ea
N
la
Ea
la
l
T
A
26

27. Расчёт устойчивости подпорной стенки

Проверка устойчивости против сдвига стенки в
27
плоскости подошвы выполняется по условию
m
Qr Qz
n
где Qr сдвигающая сила на один метр длины стенки;
m, n коэффициенты условий работы (m < 1) и
надежности по назначению сооружений ( n > 1);
Qz суммарная удерживающая сила на один метр
длины стенки.
Qr = Ea - сдвигающая сила (сила активного давления)
Qz T E p (Т – сила трения подошвы стенки о грунт)
T N tg cb где N - вес одного метра длины стенки;
b - ширина подошвы

28. Расчёт устойчивости подпорной стенки

Проверка устойчивости против
стенки выполняется по условию
28
опрокидывания
m
Mu
Mz
n
где Mu момент опрокидывающих сил относительно
ребра А; Mz момент удерживающих сил относительно
того же ребра.
M u Ea la
M z N l E pl p
где l, lp плечи силы N и силы Ер относительно точки А.

29. Устойчивость откосов и склонов

29
Устойчивость откосов и склонов
Необходимость определения устойчивости откосов и склонов
возникает при оползневых процессах, возведении и эксплуатации откосов
насыпей или выемок, строительстве на склонах или в непосредственной
близости от них.
В последнем случае устойчивость основания сооружения зачастую
определяется устойчивостью откоса, при этом его обрушение может
произойти при нагрузке меньшей, чем предельная для такого же
основания, если оно горизонтально.
Pu
f =0
f <0

30. Устойчивость откосов и склонов

30
Устойчивость откосов и склонов
Важные факторы:
-очертание склона, его крутизна и
-геологическое
строение
напластования грунтов.
характер
При неблагоприятных условиях, таких как
малая прочность грунтов, большая крутизна
склона, наличие слоя слабого водонасыщенного
глинистого
грунта,
активно
развиваются
оползневые процессы.

31. Устойчивость откосов и склонов

31
Устойчивость откосов и склонов
Устойчивость откосов и склонов традиционно
оценивается величиной, называемой коэффициентом
устойчивости:
T
k уст
Q
где T сумма силовых удерживающих факторов сил
или моментов; Q сумма соответствующих
сдвигающих факторов.
k уст 1 - склон устойчив
k уст 1 - произойдет обрушение
k уст 1 -
грунт теоретически
предельном равновесии.
должен
находится
в

32. Устойчивость откосов и склонов

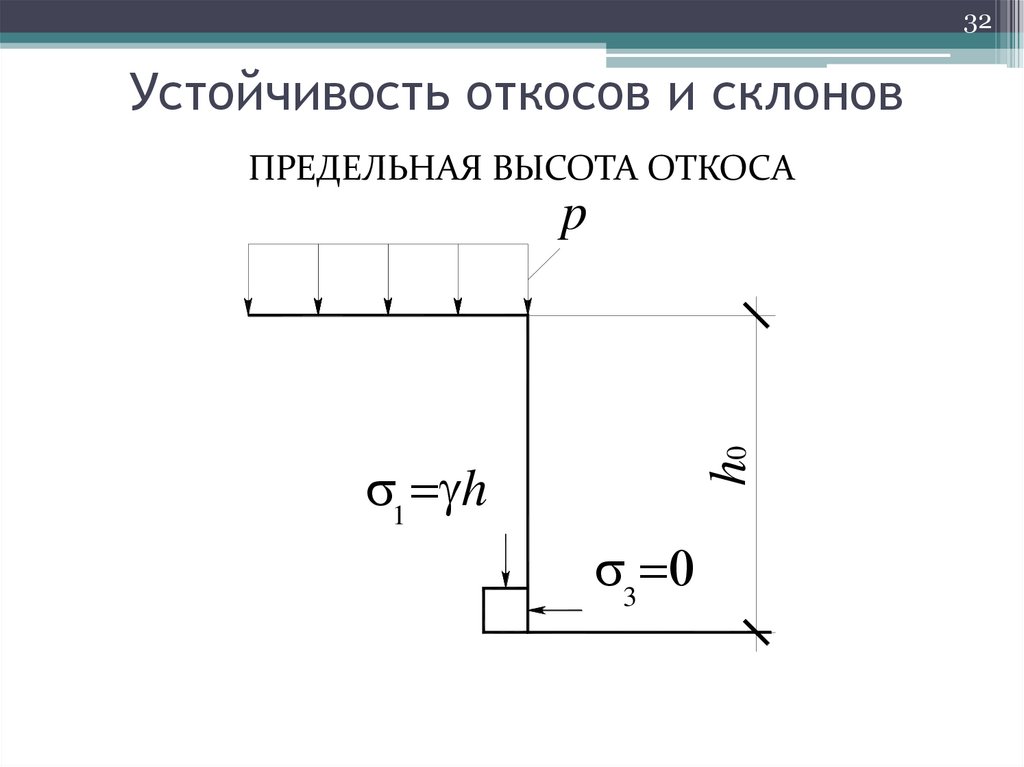
32
Устойчивость откосов и склонов
ПРЕДЕЛЬНАЯ ВЫСОТА ОТКОСА
h0
p
h
1
3

33. Устойчивость откосов и склонов

33
Устойчивость откосов и склонов
z 1 hпр p,
x 3 0
Подставим напряжения в условие прочности
Кулона Мора в главных напряжениях:
1 3 ( 1 3 2с ctg ) sin ,
hпр p ( hпр p 2с ctg ) sin ,
1 2c cos
h0
p
1 sin
Для свободного от внешней нагрузки вертикального
откоса его предельная высота определится как
2c cos
h0
.
(1 sin )

34. Устойчивость откосов и склонов

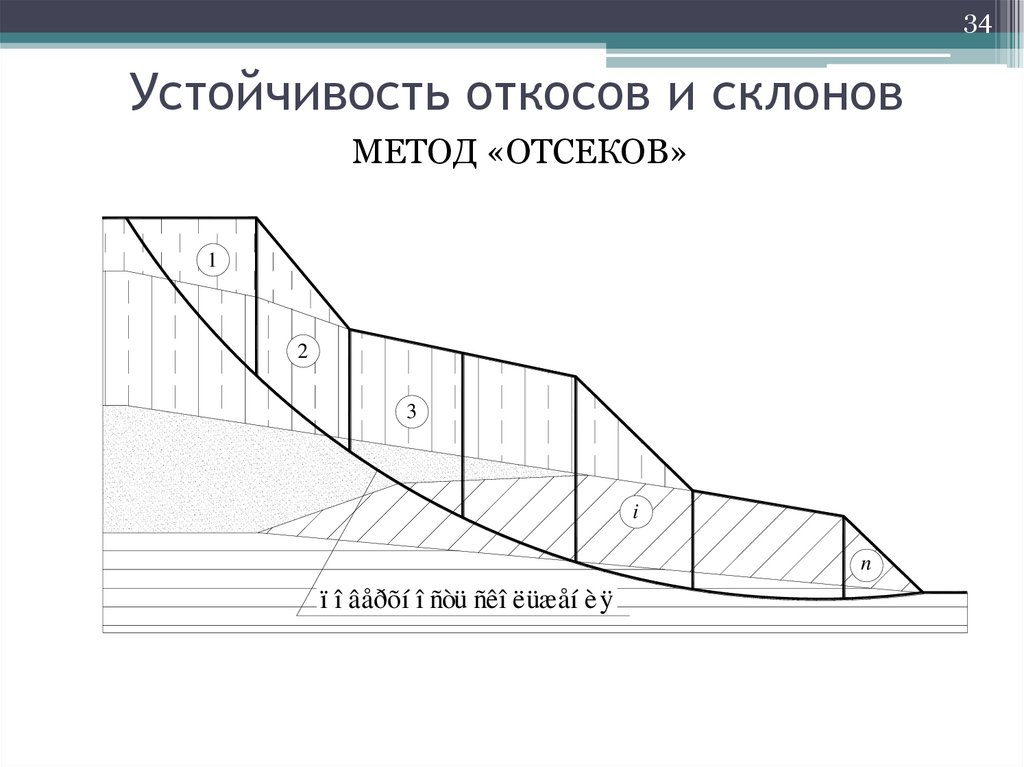
34
Устойчивость откосов и склонов
МЕТОД «ОТСЕКОВ»
1
2
3
i
n
ï î âåðõí î ñòü ñêî ëüæåí èÿ

35. Устойчивость откосов и склонов

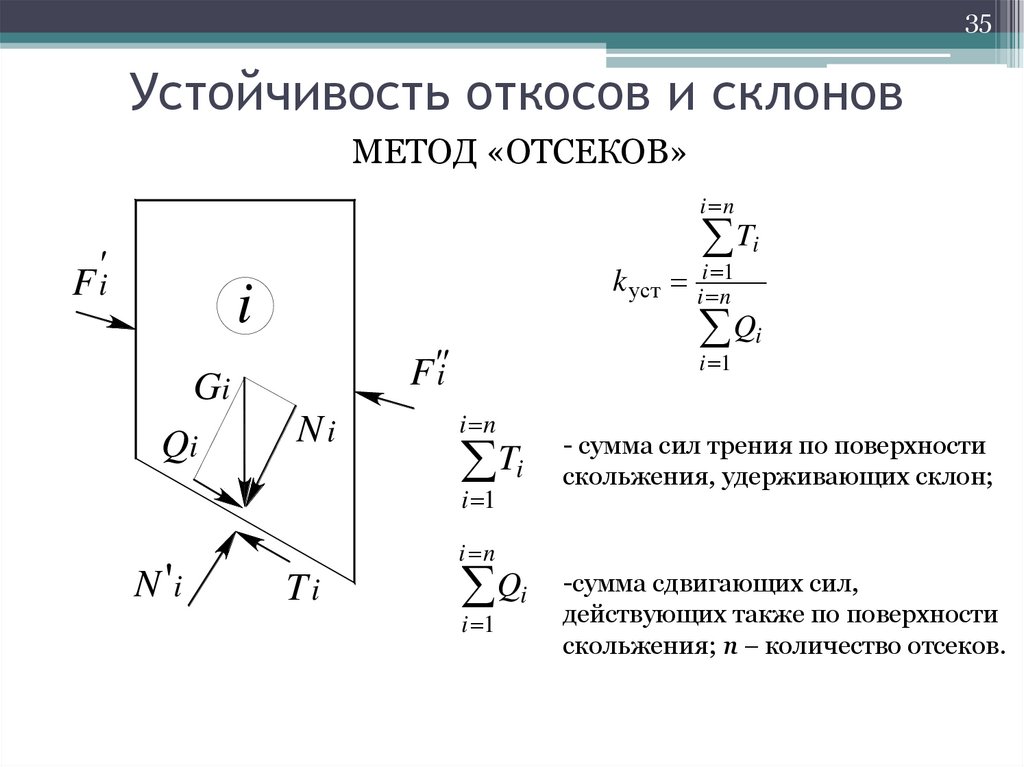
35
Устойчивость откосов и склонов
МЕТОД «ОТСЕКОВ»
i n
Ti
F'i
k уст ii n1
Qi
i
Gi
Qi
i 1
F"i
Ni
i n
Ti
i 1
N 'i
- сумма сил трения по поверхности
скольжения, удерживающих склон;
i n
Ti
Qi
i 1
-сумма сдвигающих сил,
действующих также по поверхности
скольжения; n количество отсеков.

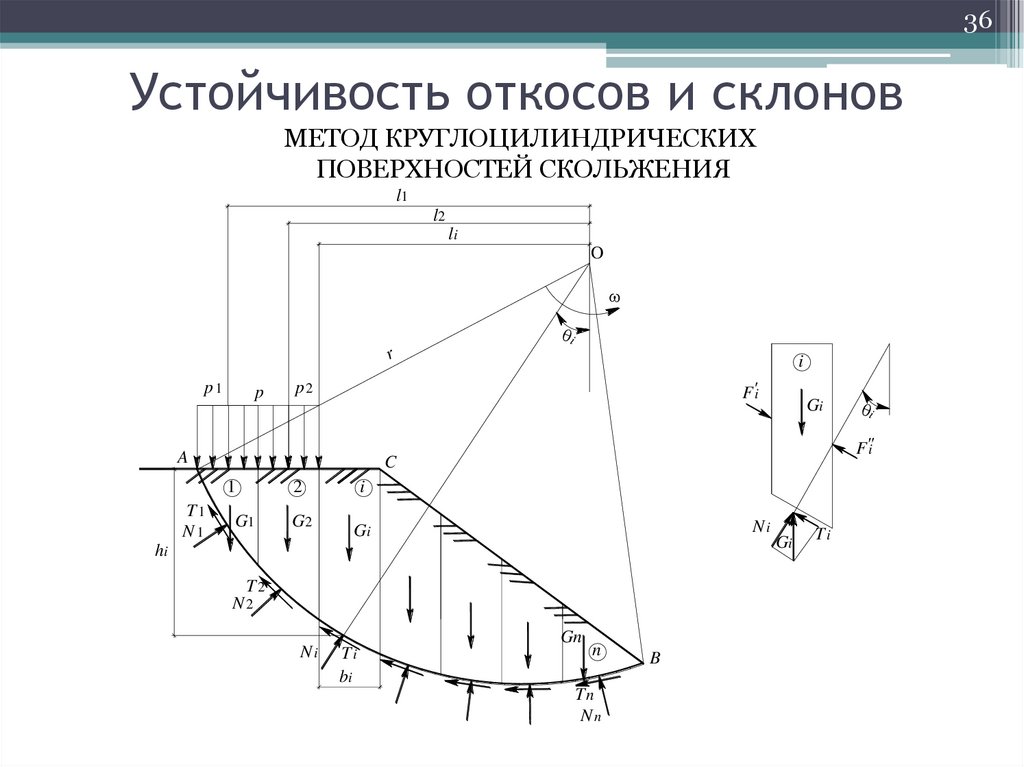
36. Устойчивость откосов и склонов

36
Устойчивость откосов и склонов
à
á
МЕТОД КРУГЛОЦИЛИНДРИЧЕСКИХ
ПОВЕРХНОСТЕЙ СКОЛЬЖЕНИЯ
l1
l2
li
O
i
r
p1
p
p2
F'i
A
T1
N1
i
Gi
F"i
C
1
2
G1
G2
i
Ni
Gi
Gi
hi
T2
N2
Ni
Gn
Ti
bi
i
n
Tn
Nn
B
Ti