Алгоритм Форда-Беллмана

1. Презентация на тему: Алгоритм Форда-Беллмана

Презентация на тему:
Алгоритм ФордаБеллмана
Выполнил
Студент первого курса
Группы б-пинж12
Карелов антон

2.

Алгоритм Форда-Беллмана – это
алгоритм для поиска кратчайших
путей из одной вершины взвешенного
графа до всех остальных. Его
достоинство в том, что он корректно
обрабатывает графы с отрицательными
весами.

3.

Вкратце разберём суть алгоритма:
Задаётся вершина, от которой необходимо
найти кратчайшие пути, и множество dist[],
содержащее расстояния от заданной
вершины до всех остальных. Изначально
dist[start] = 0 (расстояние от вершины до
себя самой), а до всех остальных оно будет
равняться бесконечности.

4.

После для каждого ребра (u, v)
проверяется условие:
если (dist[u] + вес < dist[v])
dist[v] = dist[u] + вес
Так нужно пройти по каждому ребру
в каждой итерации, которых будет
кол-во вершин - 1.

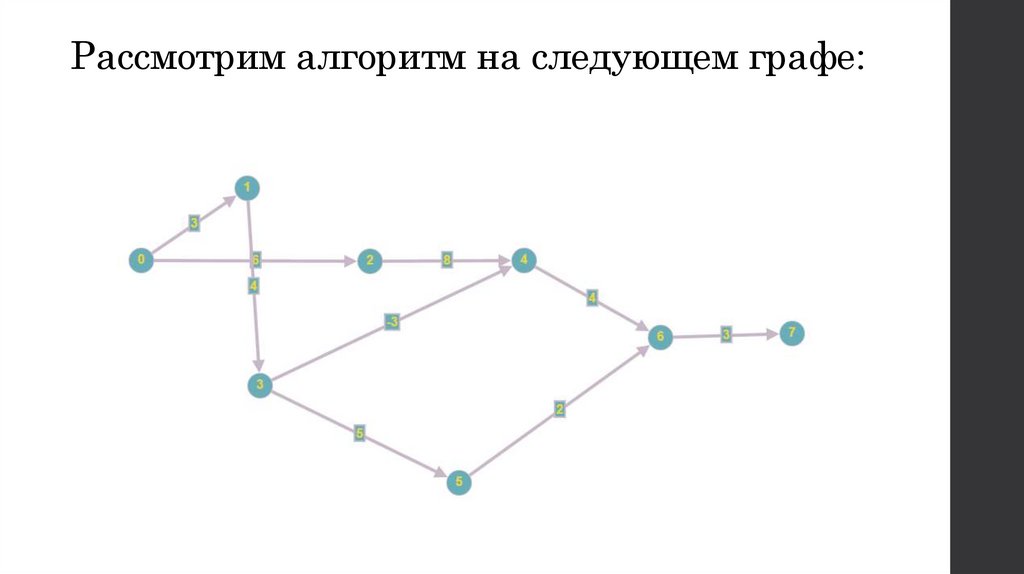
5. Рассмотрим алгоритм на следующем графе:

6. Предварительные шаги:

1. Будем искать расстояния от вершины 0.
2. Количество итераций будет равняться семи (вершин 8).
3. Зададим множество dist[8]:
dist[0] = 0
dist[1] = ∞
dist[2] = ∞
и т.д.

7. Первая итерация:

1. 0, 1: dist[0] + 3 < ∞ => dist[1] = 3
2. 0, 2: dist[0] + 6 < ∞ => dist[2] = 6
3. 1, 2: dist[1] + 4 > 6 => dist[2] не меняется
4. 1, 3: dist[1] + 4 < ∞ => dist[3] = 7
5. 2, 4: dist[2] + 8 < ∞ => dist[4] = 14
6. 3, 4: dist[3] + (-3) < 14 => dist[4] = 4
7. 3, 5: dist[3] + 5 < ∞ => dist[5] = 12
8. 4, 6: dist[4] + 4 < ∞ => dist[6] = 8
9. 5, 6: dist[5] + 2 > 8 => dist[6] не меняется
10. 6, 7: dist[6] + 3 < ∞ => dist[7] = 11
dist после первой итерации: [0, 3, 6, 7, 4, 12, 8, 11]

8. Вторая итерация

dist = [0, 3, 6, 7, 4, 12, 8, 11]
1. 0, 1: dist[0] + 3 = 3 => dist[1] не меняется
2. 0, 2: dist[0] + 6 = 6 => dist[2] не меняется
3. 1, 2: dist[1] + 4 > 6 => dist[2] не меняется
4. 1, 3: dist[1] + 4 = 7 => dist[3] не меняется
5. 2, 4: dist[2] + 8 > 4 => dist[4] не меняется
6. 3, 4: dist[3] + (-3) = 4 => dist[4] не меняется
7. 3, 5: dist[3] + 5 = 12 => dist[5] не меняется
8. 4, 6: dist[4] + 4 = 8 => dist[6] не меняется
9. 5, 6: dist[5] + 2 > 8 => dist[6] не меняется
10. 6, 7: dist[6] + 3 = 11 => dist[7] не меняется