Правильные многогранники. Платоновы тела

1. ПРАВИЛЬНЫЕ МНОГОГРАННИКИ

«ПЛАТОНОВЫ ТЕЛА»
Подготовили: Лукошин Владислав
Жукалов Андрей
ученики 10 «А» класса

2.

Многогранник называется правильным, если:
многогранник выпуклый;
все его грани — равные правильные многоугольники;
в каждой его вершине сходится одно и то же число рёбер.

3.

Немного истории
Правильные многогранники известны с древнейших
времён. Их орнаментные модели можно найти на резных
каменных шарах, созданных в период позднего неолита, в
Шотландии. В костях, которыми люди играли на заре
цивилизации,
уже
угадываются
формы
Резной каменный шар
правильных
многогранников.
Игральная кость

4.

В
значительной
многогранники
мере
были
правильные
изучены
древними
греками. Некоторые источники приписывают
честь их открытия Пифагору.
Пифагорейцы
считали
правильные
многогранники божественными фигурами и
использовали
в
своих
философских
сочинениях.
Их
поражала
совершенство, гармония этих фигур.
Пифагор Самосский
(около 570 - 490 годов до н. э.)
красота,

5.

Правильные многогранники характерны для философии Платона, в
честь которого и получили название «Платоновы тела».
Платон писал о них в своём трактате «Тимей», где сопоставил
каждую из четырёх стихий и вселенной определённому правильному
Платон
многограннику.
воздух - октаэдр
огонь - тетраэдр
земля - гексаэдр (куб)
вселенная - додекаэдра
вода — икосаэдр

6.

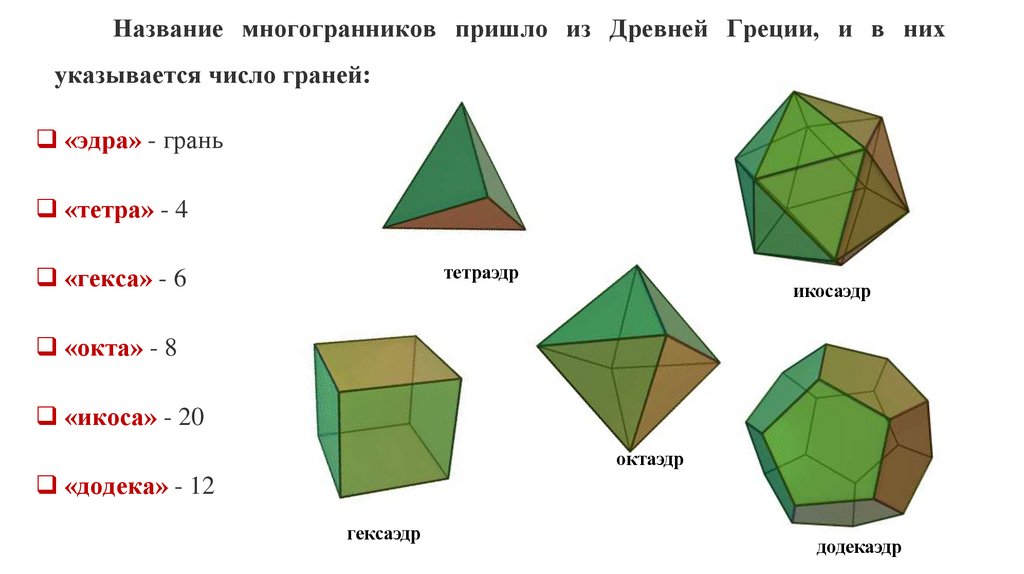
Название многогранников пришло из Древней Греции, и в них
указывается число граней:
«эдра» - грань
«тетра» - 4
тетраэдр
«гекса» - 6
икосаэдр
«окта» - 8
«икоса» - 20
октаэдр
«додека» - 12
гексаэдр
додекаэдр

7.

Возникает вопрос
Какие правильные многоугольники
правильного многогранника?
могут
быть
гранями
1. У правильного n-угольника, если n ≥ 6, углы не меньше 120°.
2. В каждой вершине многогранника должно быть не меньше
трёх углов.
3. Даже при трёх углах сумма всех углов уже достигает 360°.
4. Сумма всех плоских углов при каждой вершине выпуклого
многогранника меньше 360°.
Следовательно, не существует правильного многогранника,
гранями которого являлись бы правильные n-угольники,
если n ≥ 6.
Только правильные треугольники, четырёхугольники
(квадраты) и пятиугольники могут быть гранями правильного
многогранника.
В соответствии с этим получаем следующие многогранники
(их всего 5).
правильный
шестиугольник
120° * 3 = 360°
правильный
семиугольник
128,57° * 3 = 385,71°
правильный
восьмиугольник
135° * 3 = 405°

8.

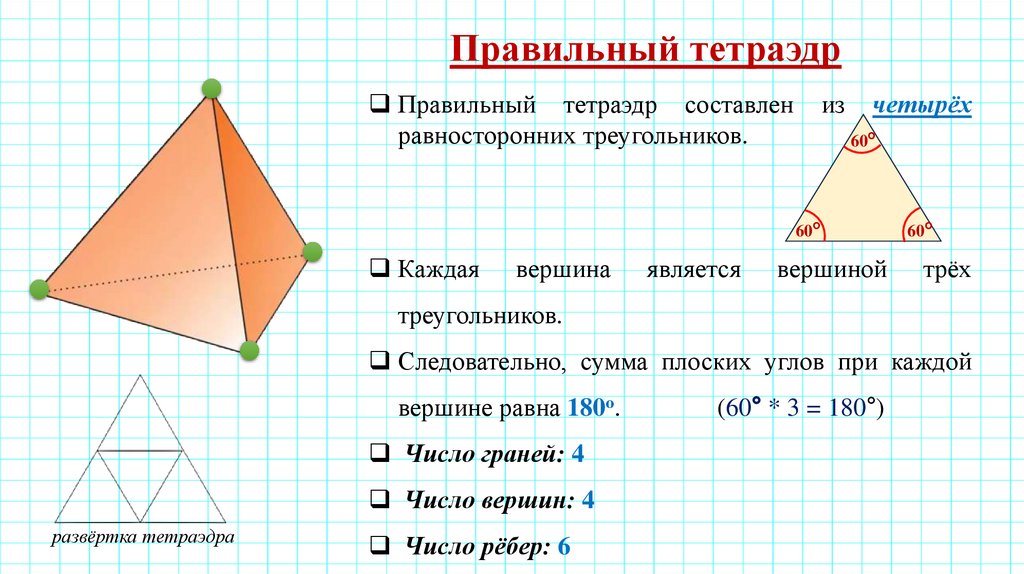
Правильный тетраэдр
Правильный тетраэдр составлен
равносторонних треугольников.
из
четырёх
60°
60°
Каждая
вершина
является
вершиной
60°
трёх
треугольников.
Следовательно, сумма плоских углов при каждой
вершине равна 180о.
Число граней: 4
Число вершин: 4
развёртка тетраэдра
Число рёбер: 6
(60° * 3 = 180°)

9.

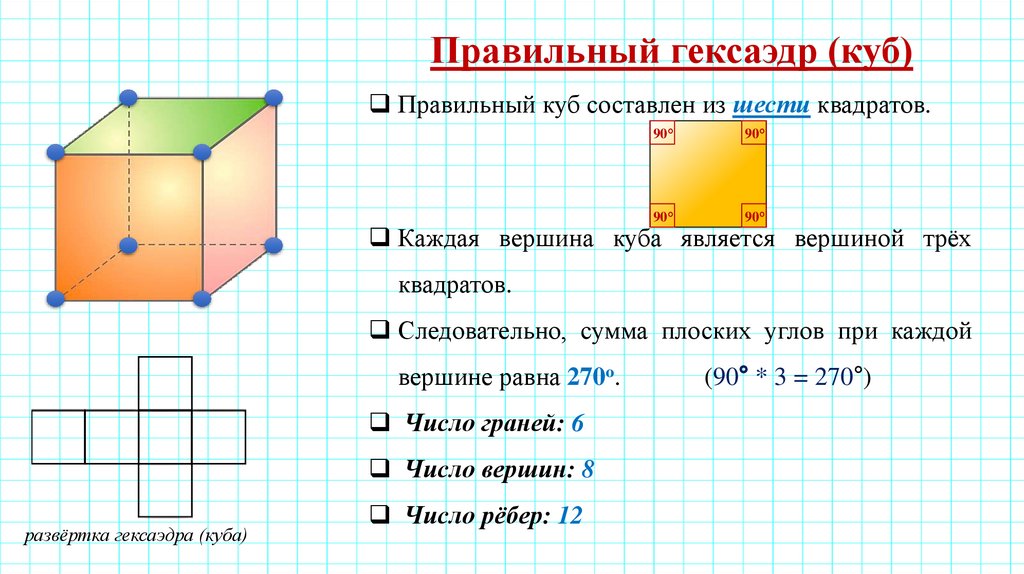
Правильный гексаэдр (куб)
Правильный куб составлен из шести квадратов.
90°
90°
90°
90°
Каждая вершина куба является вершиной трёх
квадратов.
Следовательно, сумма плоских углов при каждой
вершине равна 270о.
Число граней: 6
Число вершин: 8
развёртка гексаэдра (куба)
Число рёбер: 12
(90° * 3 = 270°)

10.

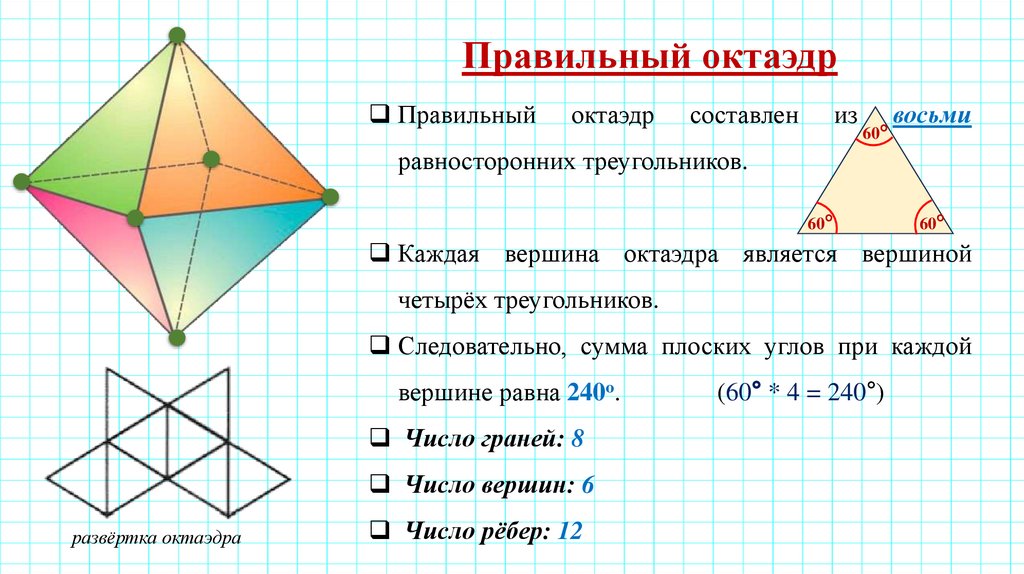
Правильный октаэдр
Правильный
октаэдр
составлен
из
60°
восьми
равносторонних треугольников.
60°
60°
Каждая вершина октаэдра является вершиной
четырёх треугольников.
Следовательно, сумма плоских углов при каждой
вершине равна 240о.
Число граней: 8
Число вершин: 6
развёртка октаэдра
Число рёбер: 12
(60° * 4 = 240°)

11.

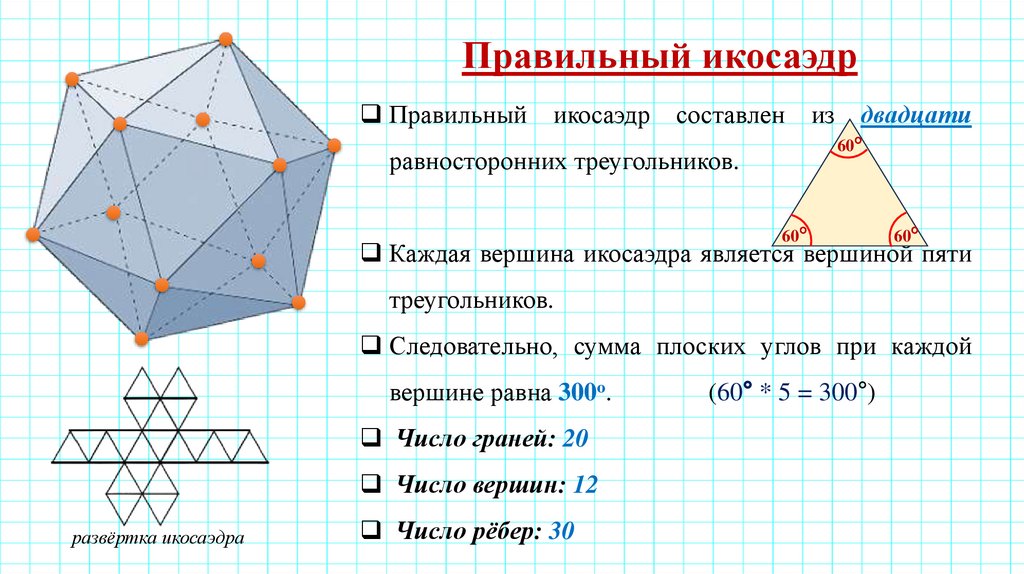
Правильный икосаэдр
Правильный
икосаэдр
составлен
из
двадцати
60°
равносторонних треугольников.
60°
60°
Каждая вершина икосаэдра является вершиной пяти
треугольников.
Следовательно, сумма плоских углов при каждой
вершине равна 300о.
Число граней: 20
Число вершин: 12
развёртка икосаэдра
Число рёбер: 30
(60° * 5 = 300°)

12.

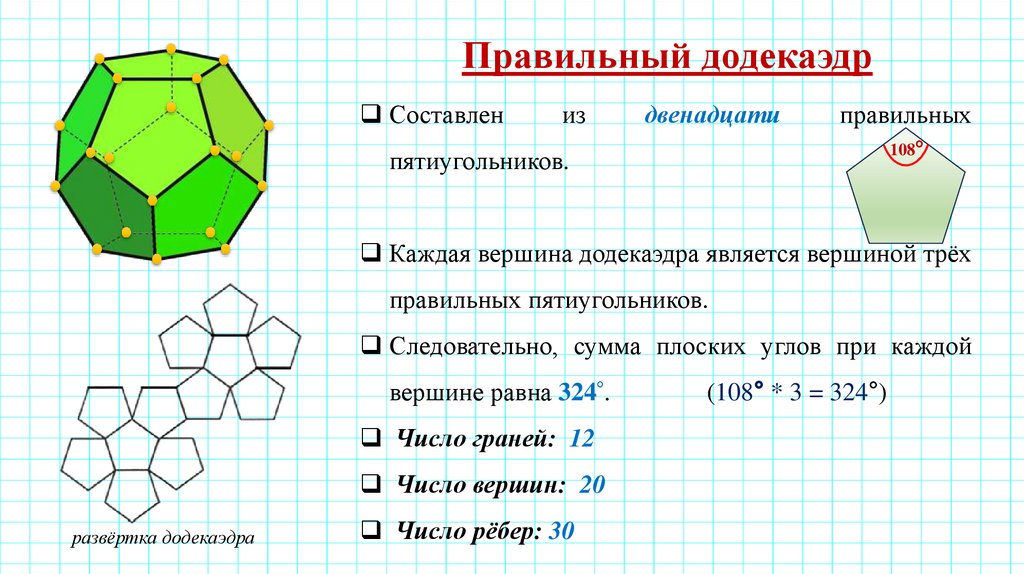
Правильный додекаэдр
Составлен
из
двенадцати
правильных
108°
пятиугольников.
Каждая вершина додекаэдра является вершиной трёх
правильных пятиугольников.
Следовательно, сумма плоских углов при каждой
вершине равна 324°.
Число граней: 12
Число вершин: 20
развёртка додекаэдра
Число рёбер: 30
(108° * 3 = 324°)

13.

Теорема Эйлера и правильные многогранники
Теорема Эйлера: В любом выпуклом многограннике сумма
числа граней и числа вершин больше числа рёбер на 2.
Пусть, В – число вершин выпуклого многогранника;
Р – число его рёбер;
Г – число граней.
Тогда верно равенство: Г + В = Р + 2
Г+В-Р=2

14.

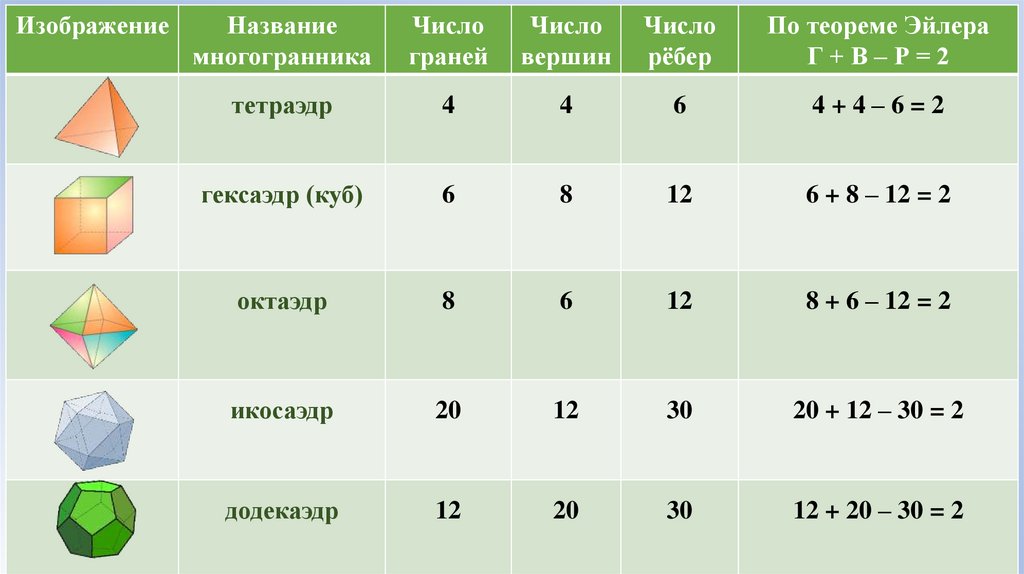
Изображение
Название
многогранника
Число
граней
Число
вершин
Число
рёбер
По теореме Эйлера
Г+В–Р=2
тетраэдр
4
4
6
4+4–6=2
гексаэдр (куб)
6
8
12
6 + 8 – 12 = 2
октаэдр
8
6
12
8 + 6 – 12 = 2
икосаэдр
20
12
30
20 + 12 – 30 = 2
додекаэдр
12
20
30
12 + 20 – 30 = 2

15.

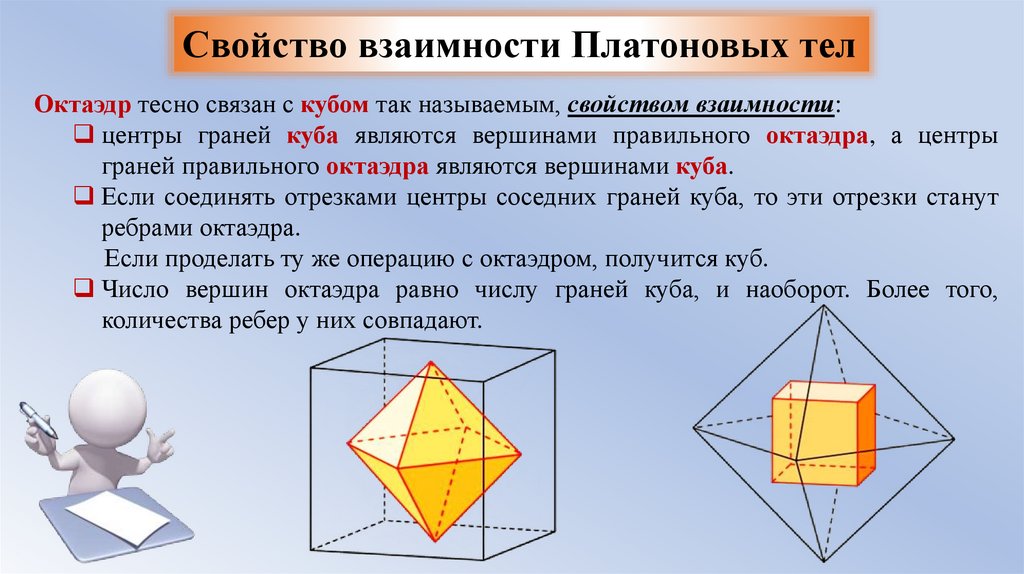
Свойство взаимности Платоновых тел
Октаэдр тесно связан с кубом так называемым, свойством взаимности:
центры граней куба являются вершинами правильного октаэдра, а центры
граней правильного октаэдра являются вершинами куба.
Если соединять отрезками центры соседних граней куба, то эти отрезки станут
ребрами октаэдра.
Если проделать ту же операцию с октаэдром, получится куб.
Число вершин октаэдра равно числу граней куба, и наоборот. Более того,
количества ребер у них совпадают.

16.

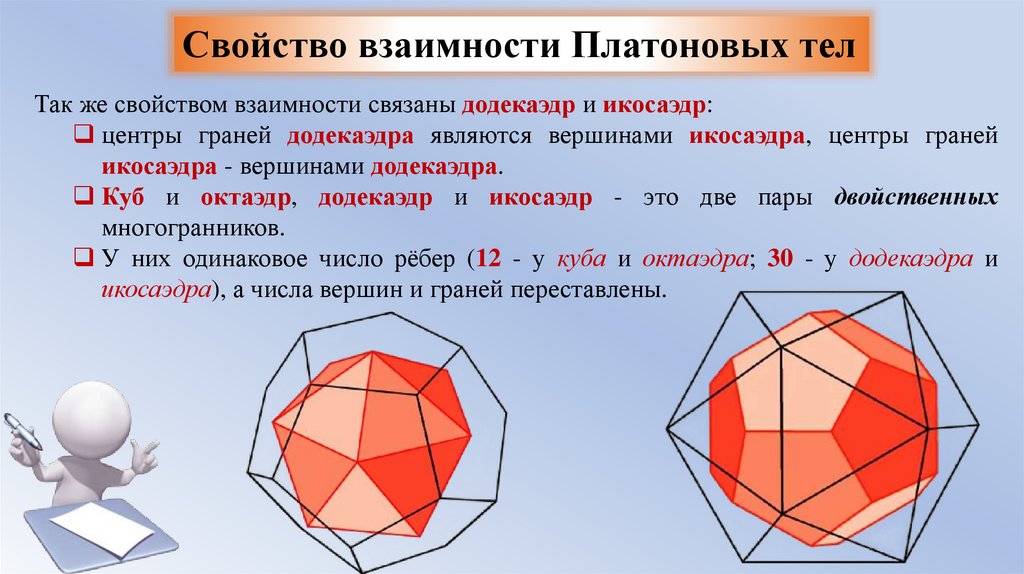
Свойство взаимности Платоновых тел
Так же свойством взаимности связаны додекаэдр и икосаэдр:
центры граней додекаэдра являются вершинами икосаэдра, центры граней
икосаэдра - вершинами додекаэдра.
Куб и октаэдр, додекаэдр и икосаэдр - это две пары двойственных
многогранников.
У них одинаковое число рёбер (12 - у куба и октаэдра; 30 - у додекаэдра и
икосаэдра), а числа вершин и граней переставлены.

17.

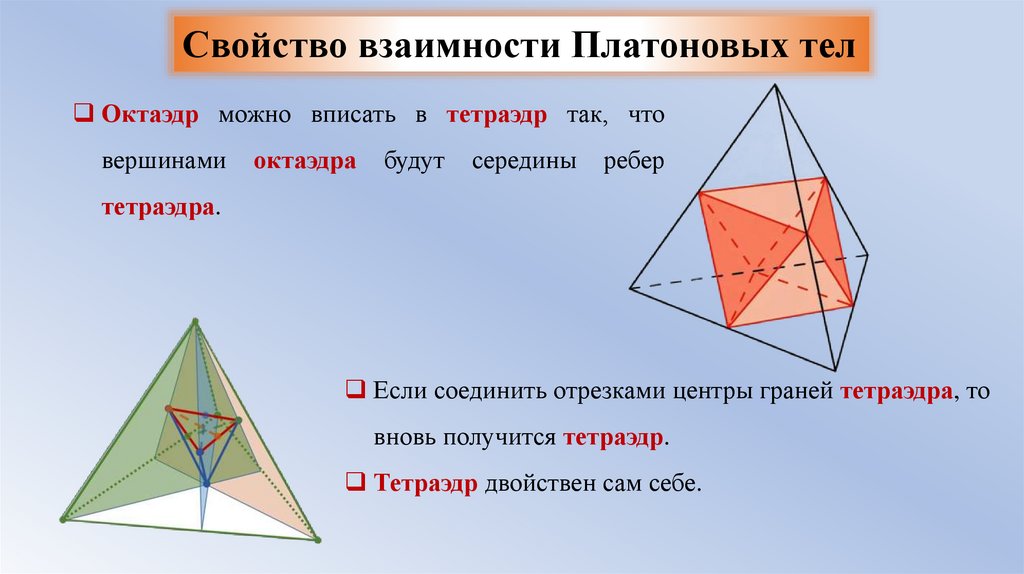
Свойство взаимности Платоновых тел
Октаэдр можно вписать в тетраэдр так, что
вершинами
октаэдра
будут
середины
ребер
тетраэдра.
Если соединить отрезками центры граней тетраэдра, то
вновь получится тетраэдр.
Тетраэдр двойствен сам себе.

18.

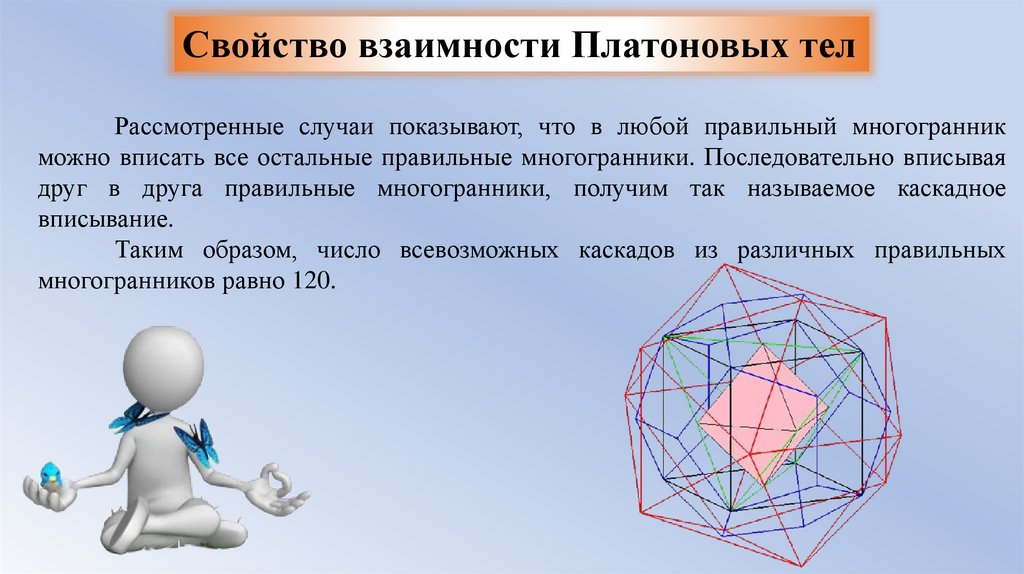
Свойство взаимности Платоновых тел
Рассмотренные случаи показывают, что в любой правильный многогранник
можно вписать все остальные правильные многогранники. Последовательно вписывая
друг в друга правильные многогранники, получим так называемое каскадное
вписывание.
Таким образом, число всевозможных каскадов из различных правильных
многогранников равно 120.

19.

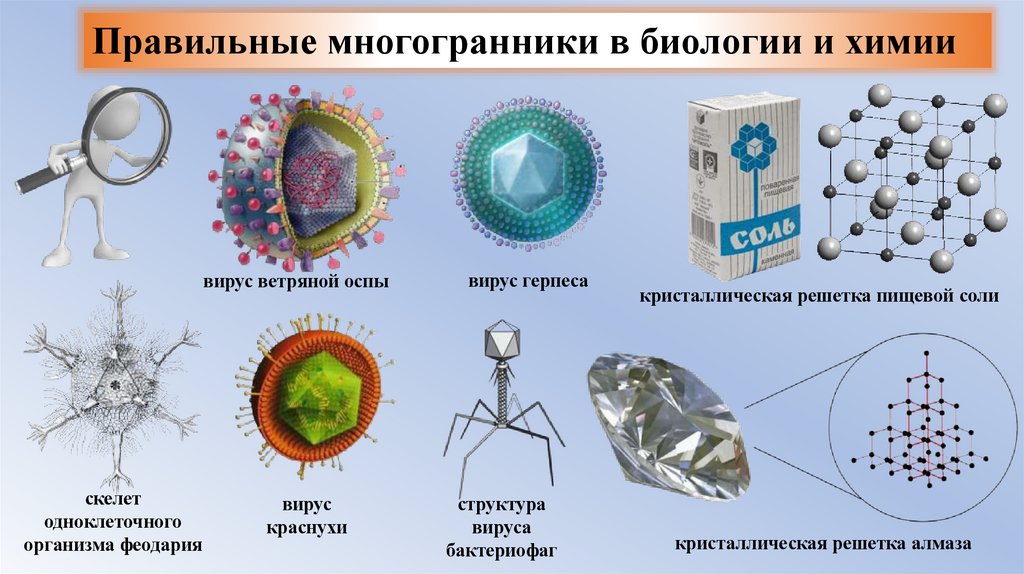
Правильные многогранники в биологии и химии
вирус ветряной оспы
скелет
одноклеточного
организма феодария
вирус
краснухи
вирус герпеса
структура
вируса
бактериофаг
кристаллическая решетка пищевой соли
кристаллическая решетка алмаза

20.

Правильные многогранники в архитектуре
Лувр. Париж
Кааба в Мекке
Спортивный
комплекс
г. Новосибирск
Пирамида в Египте

21.

Правильные многогранники в играх
Дайсы
Кубик Рубика

22.

Правильные многогранники в моде

23.

Правильные многогранники в быту

24.

Правильные многогранники в инсталляции

25.

СПАСИБО ЗА ВНИМАНИЕ!