Касание окружностей

1.

Касание
окружностей

2.

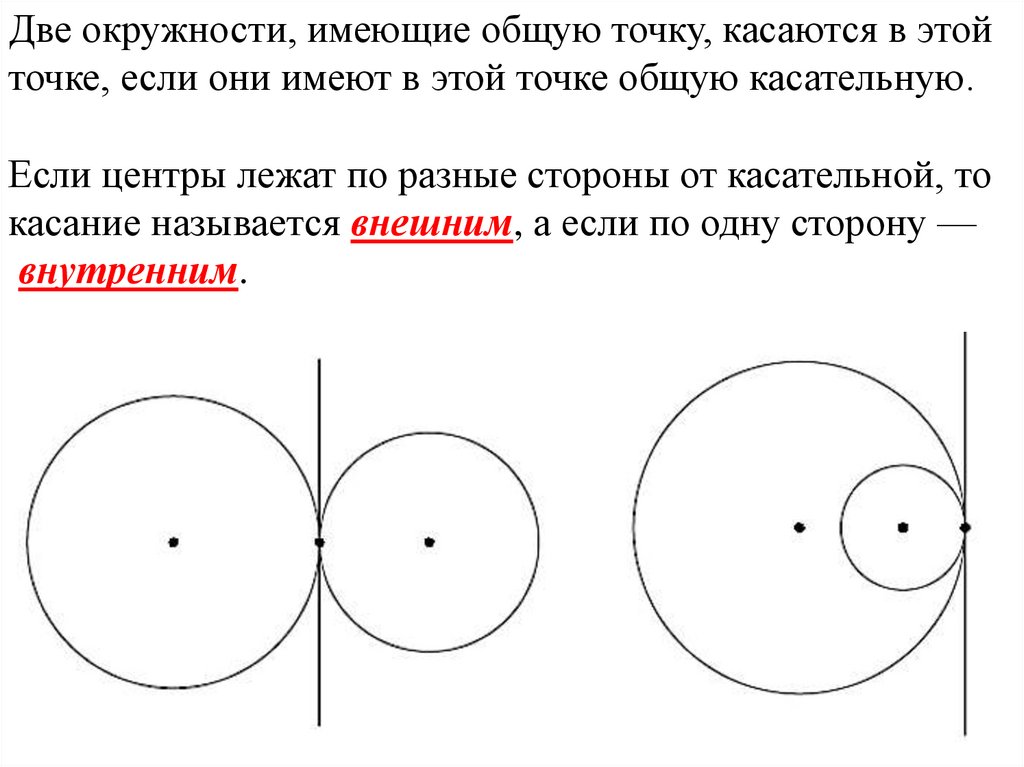
Две окружности, имеющие общую точку, касаются в этой
точке, если они имеют в этой точке общую касательную.
Если центры лежат по разные стороны от касательной, то
касание называется внешним, а если по одну сторону —
внутренним.

3.

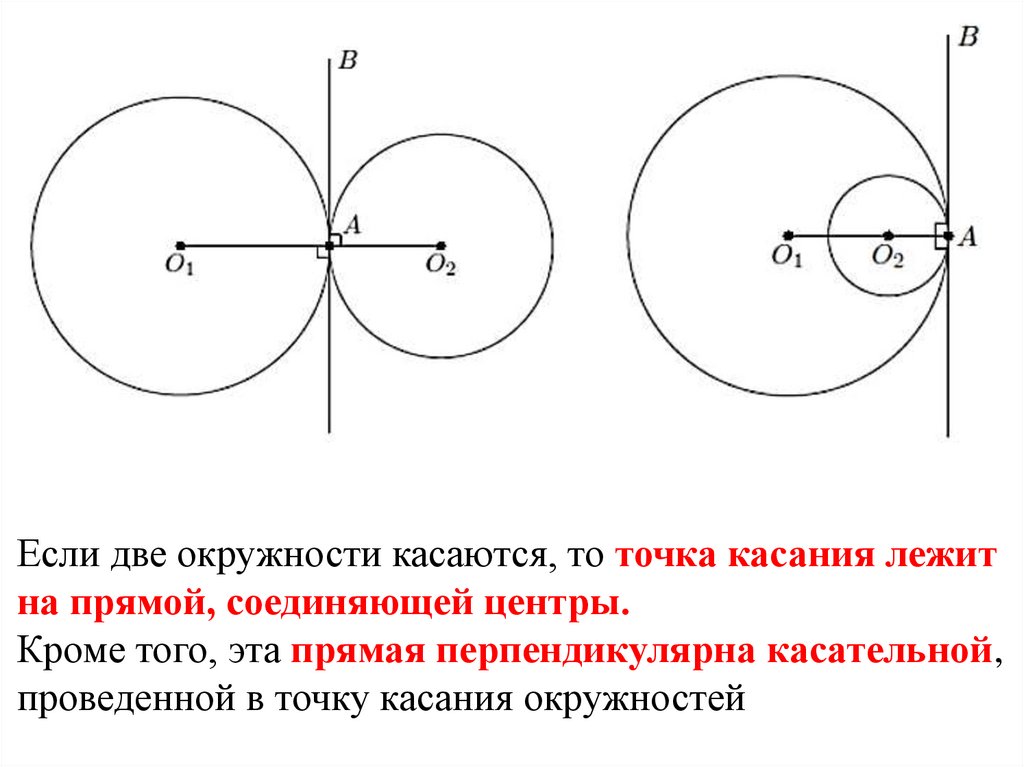
Если две окружности касаются, то точка касания лежит
на прямой, соединяющей центры.
Кроме того, эта прямая перпендикулярна касательной,
проведенной в точку касания окружностей

4.

5.

6.

7.

8.

9.

10.

11.

12. Заполните таблицу.

Радиус первой окружности, см
6
3
6
3
3
5
Радиус второй окружности, см
2
2
4
4
4
2
Расстояние между центрами
окружностей, см
3
5
12
5
0
9
Вывод о взаимном
расположении
окружностей

13.

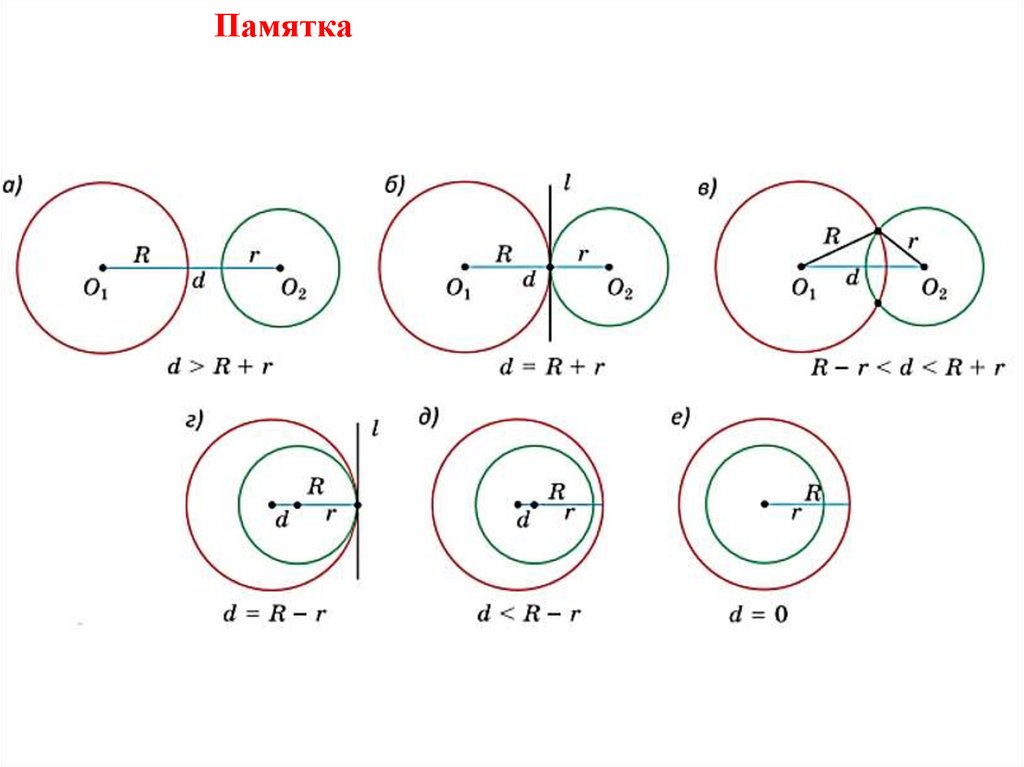
Памятка
Для двух окружностей с радиусами R и r (R > r) и
расстоянием d = O1O2 между их центрами можно выделить
шесть случаев их различного взаимного расположения на
плоскости:
а) окружности расположены внешним образом и не
касаются: d > R + r;
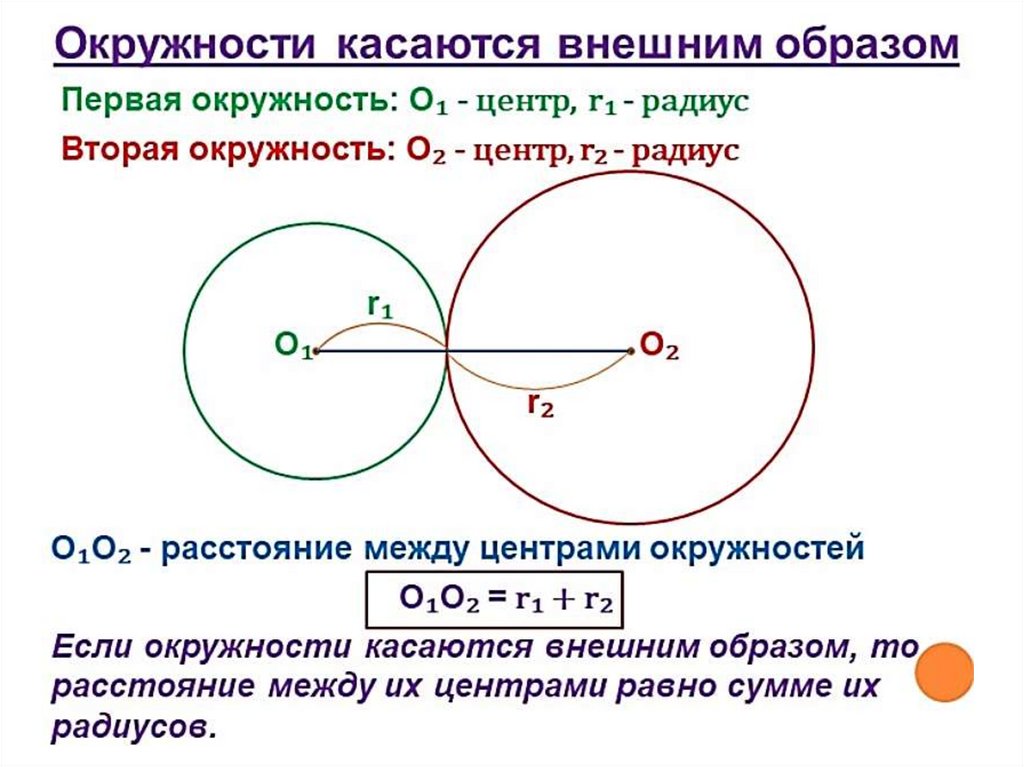
б) окружности касаются внешним образом: d = R + r;
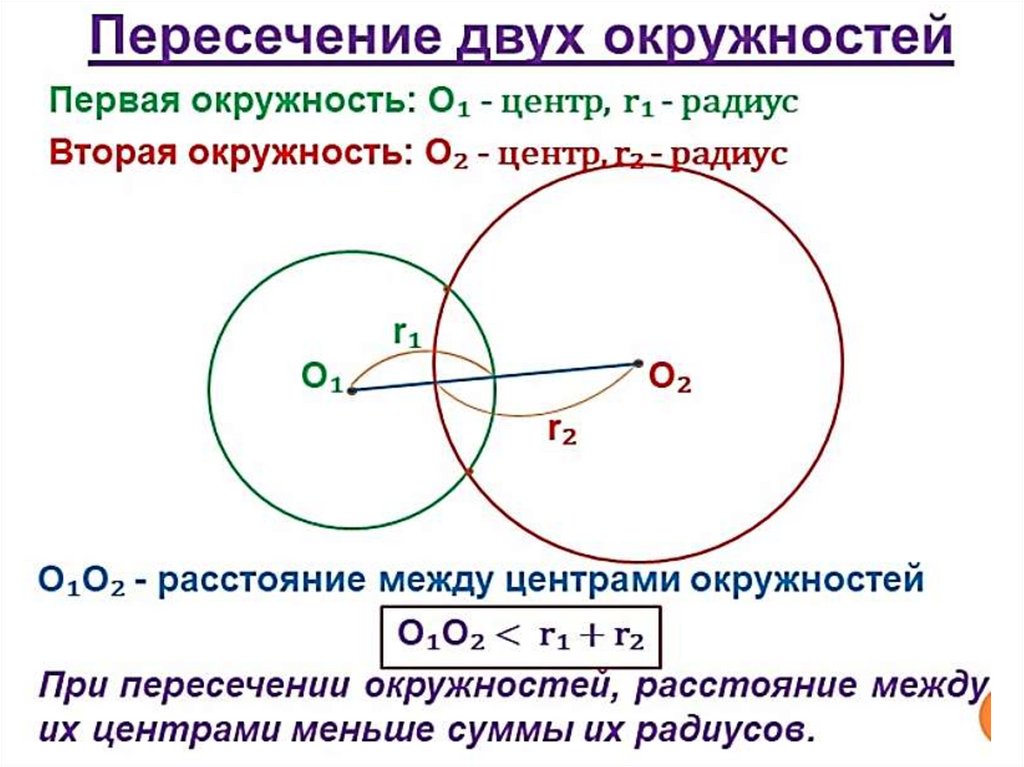
в) окружности пересекаются (в 2 точках): R − r < d < R + r
(неравенство треугольника);
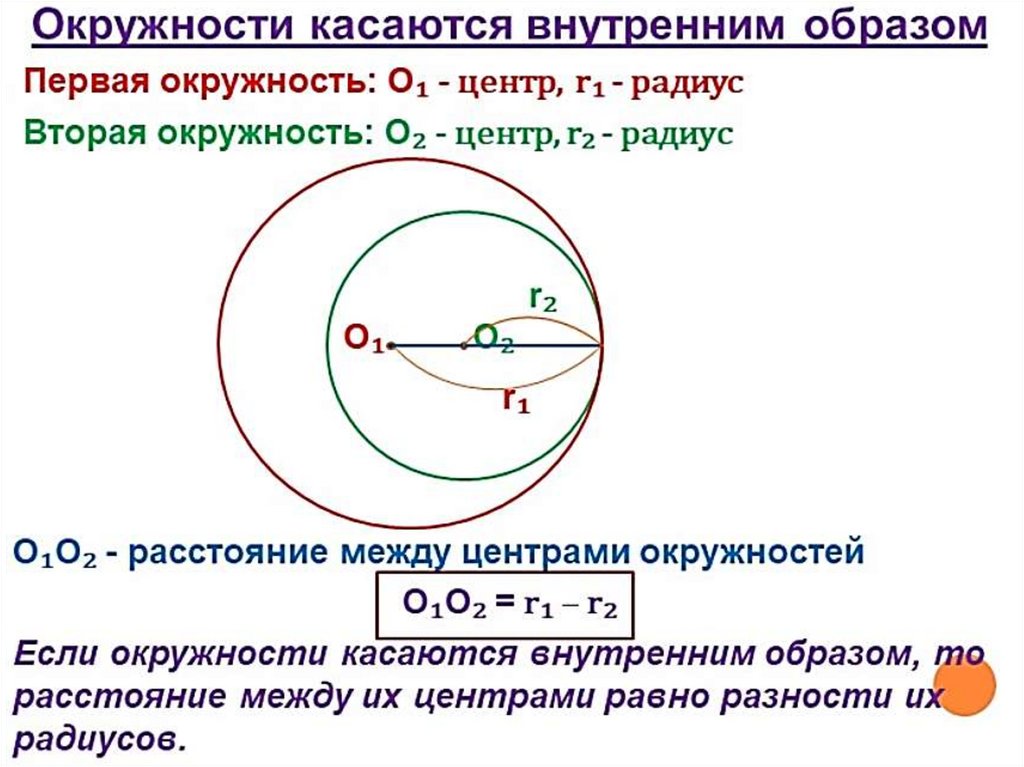
г) окружности касаются внутренним образом: d = R − r;
д) окружности расположены внутренним образом, не
касаются, и их центры не совпадают: d < R − r;
е) окружности расположены внутренним образом, их
центры совпадают (концентрические окружности): d = 0.

14.

Памятка