prezentatsiya-k-uroku-geometrii-po-teme-vzaimnoe-raspolozhenie-dvuh-okruzhnostej

1.

Взаимное расположение двух
окружностей, общие
касательные. Касание
окружностей
Подготовила:
учитель математики
МБОУ Г.ГОРЛОВКИ «ШКОЛА № 42
Рыбина М.В.

2.

Две
окружности могут пересекаться, не пересекаться либо касаться друг
.
друга.
Перейдем к анализу возможных случаев расположения двух окружностей.
Рассмотрим окружность с центром О1 и окружность с центром О2. Тогда
расстояние между их центрами равно О1О2.
Пересекающиеся окружности имеют две общие точки.
Расстояние между центрами двух пересекающихся окружностей
больше разности, но меньше суммы их радиусов:

3.

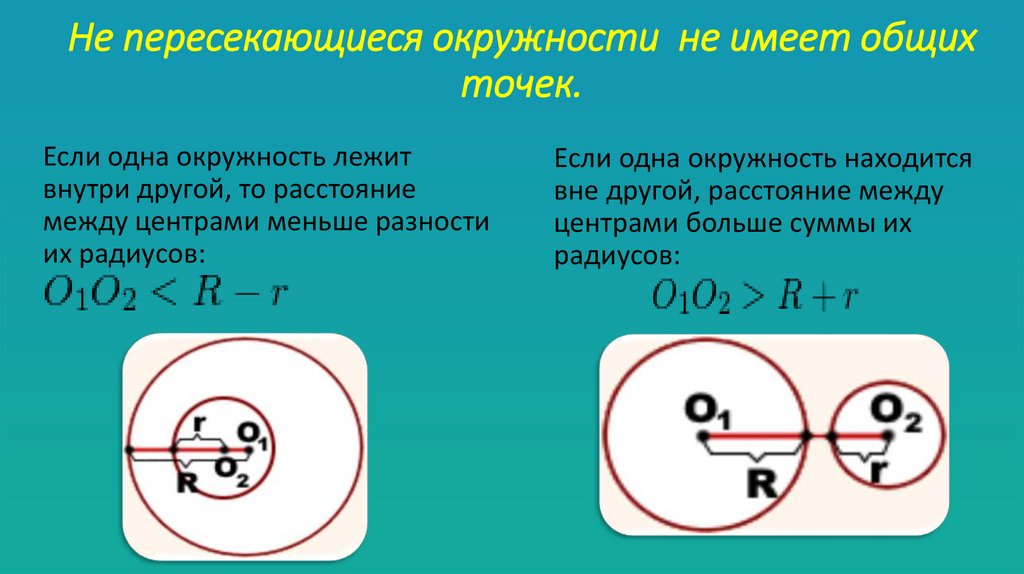
Не пересекающиеся окружности не имеет общих
точек.
Если одна окружность лежит
внутри другой, то расстояние
между центрами меньше разности
их радиусов:
Если одна окружность находится
вне другой, расстояние между
центрами больше суммы их
радиусов:

4.

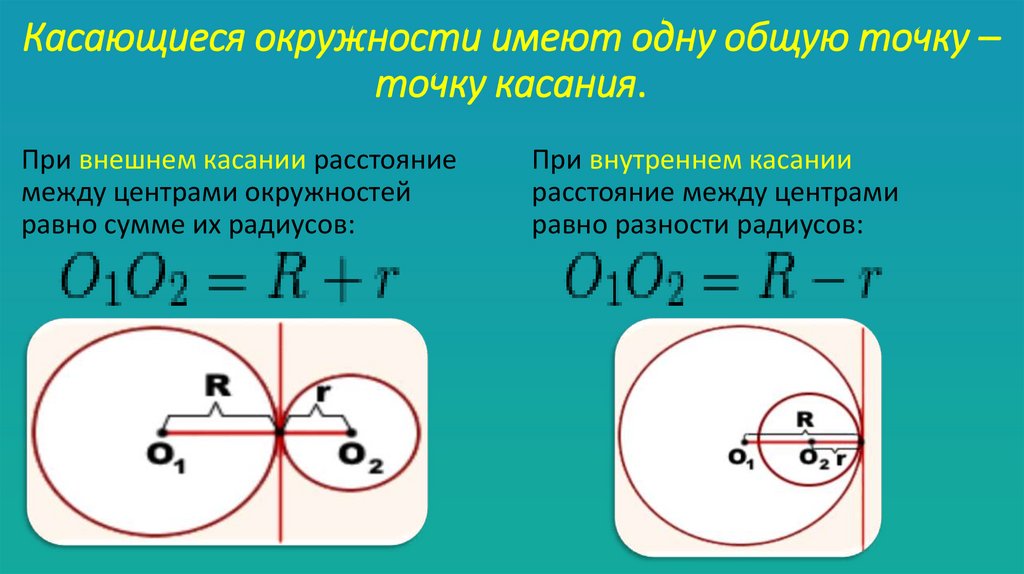
Касающиеся окружности имеют одну общую точку –
точку касания.
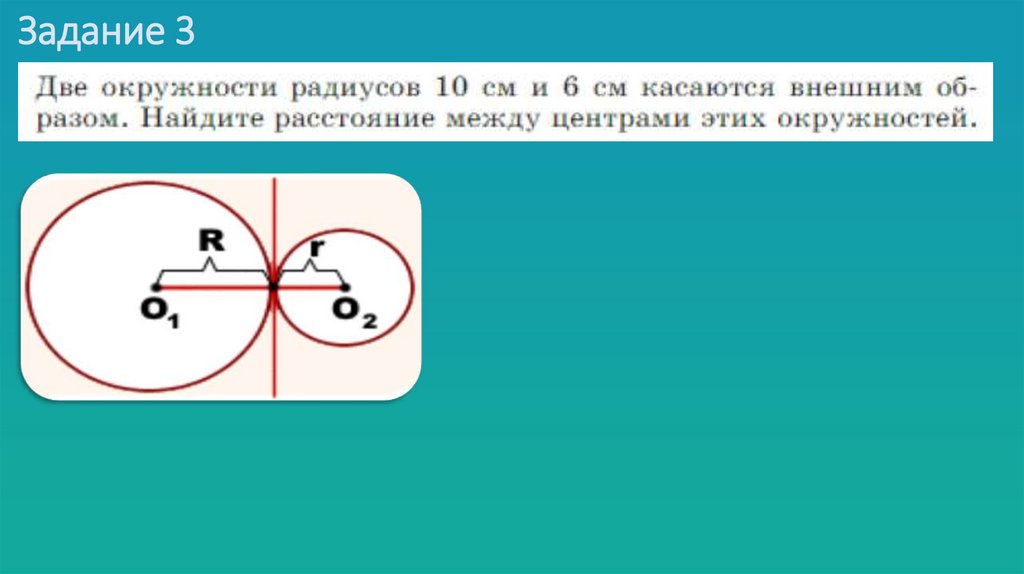
При внешнем касании расстояние
между центрами окружностей
равно сумме их радиусов:
При внутреннем касании
расстояние между центрами
равно разности радиусов:

5.

Если центры окружностей совпадают, то такие окружности называются
концентрическими.
Концентрические окружности разного радиуса не пересекаются: О1О2 = 0
В случае равенства радиусов они совпадают.
Если же радиусы этих окружностей не равны, то одна из них лежит внутри
другой – образуется кольцо.
Кольцом называют фигуру, заключенную между концентрическими
окружностями.

6.

Лемма
Если для длин a,b и c трех данных отрезков выполняются
условия:
то существует треугольник,
стороны которого равны данным отрезкам.

7.

Теорема о взаимном расположении двух
окружностей
Пусть центры О и О двух окружностей с радиусами R и r не
совпадают, О О = d, тогда:
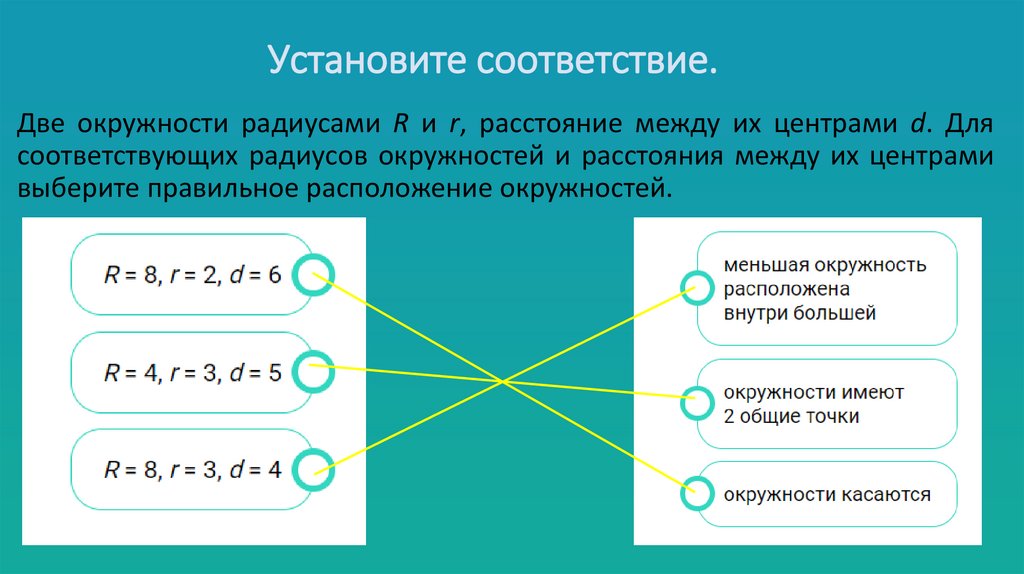
1) окружности пересекаются, если R - r < d < R + r и R r ;
2) окружности касаются внешним образом, если d = R + r;
3) окружности касаются внутренним образом, если
d = R - r и R > r;
4) окружности не имеют общих точек, причем окружность с
центром О расположена вне окружности с центром О , если
d > R + r;
5) окружности не имеют общих точек, причем окружность с
центром О расположена внутри окружности с центром О ,
если d < R - r и R > r
1
1
2
2
2
2
1
1

8.

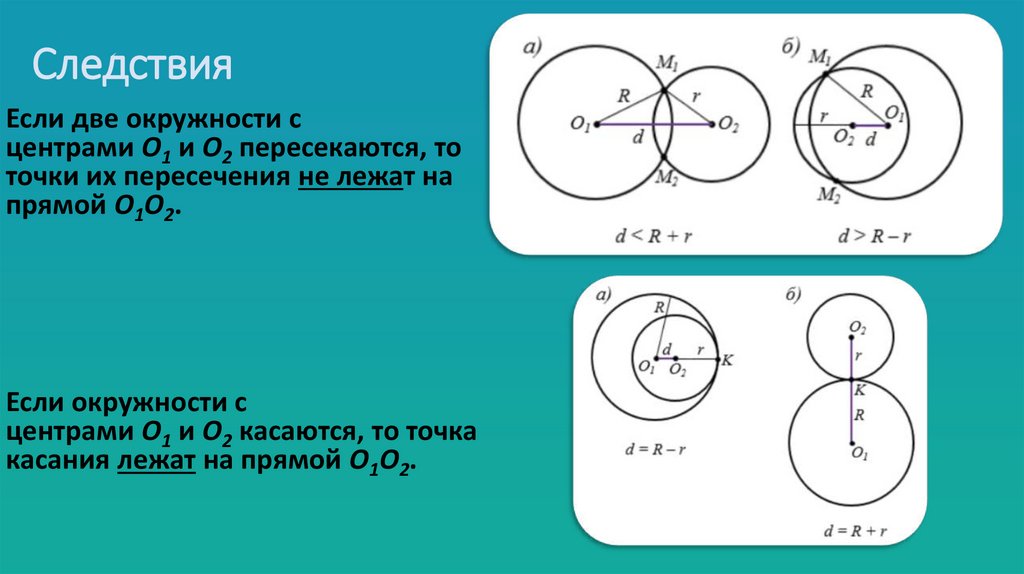
Следствия
Если две окружности с
центрами О1 и О2 пересекаются, то
точки их пересечения не лежат на
прямой О1О2.
Если окружности с
центрами О1 и О2 касаются, то точка
касания лежат на прямой О1О2.

9.

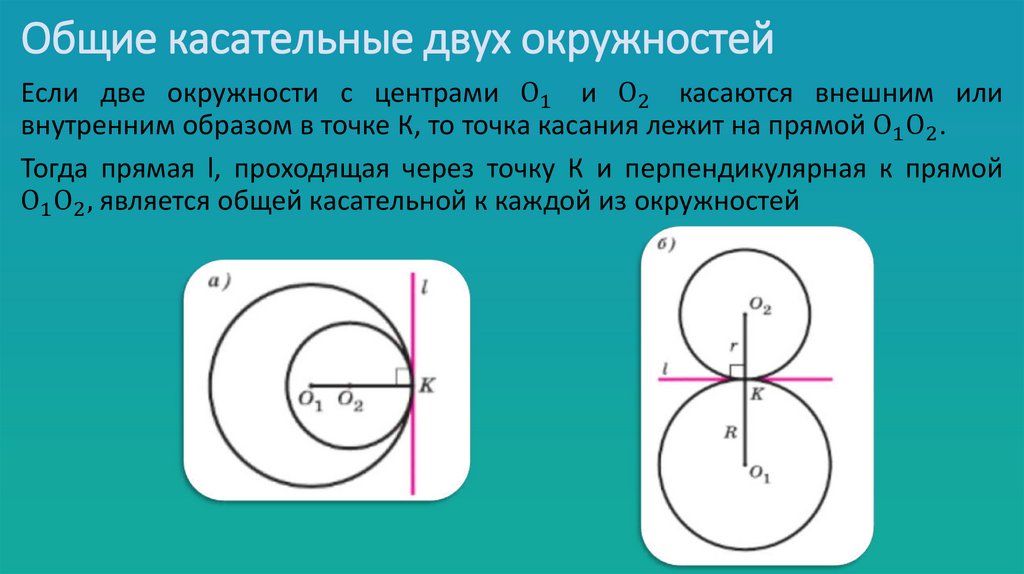
Общие касательные двух окружностей
Если две окружности с центрами О1 и О2 касаются внешним или
внутренним образом в точке К, то точка касания лежит на прямой О1 О2 .
Тогда прямая l, проходящая через точку К и перпендикулярная к прямой
О1 О2 , является общей касательной к каждой из окружностей

10.

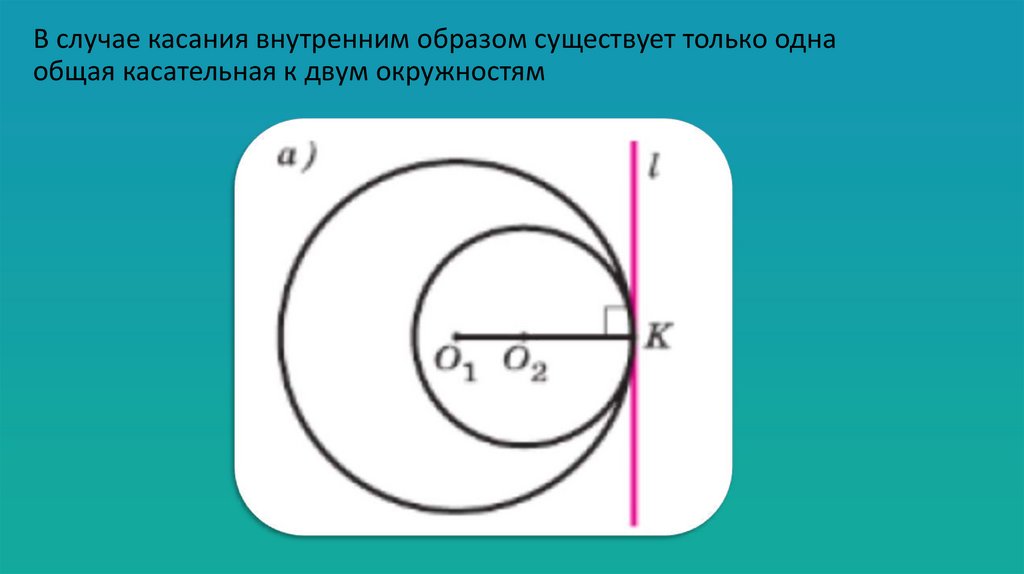
В случае касания внутренним образом существует только одна
общая касательная к двум окружностям

11.

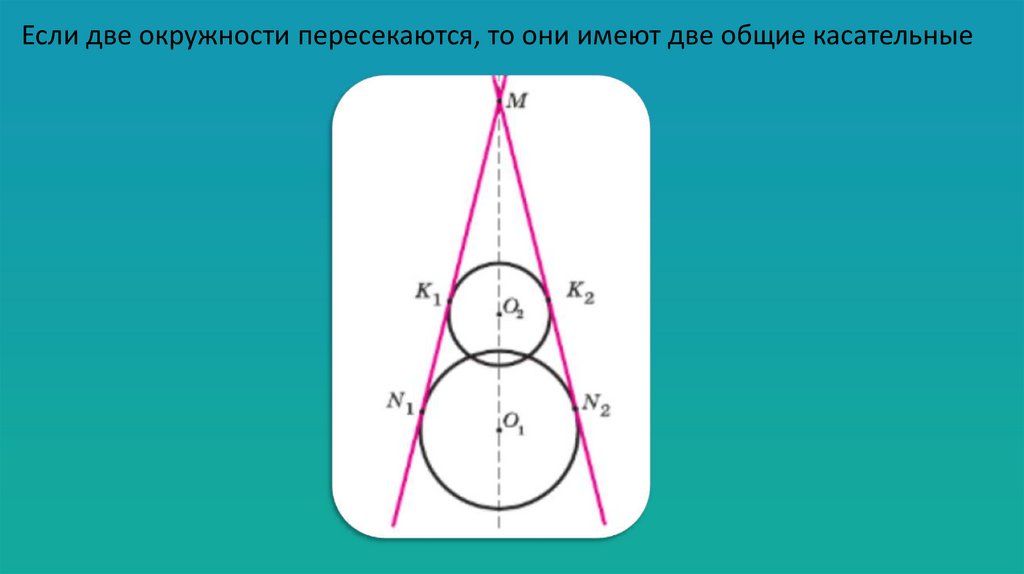
Если две окружности пересекаются, то они имеют две общие касательные

12.

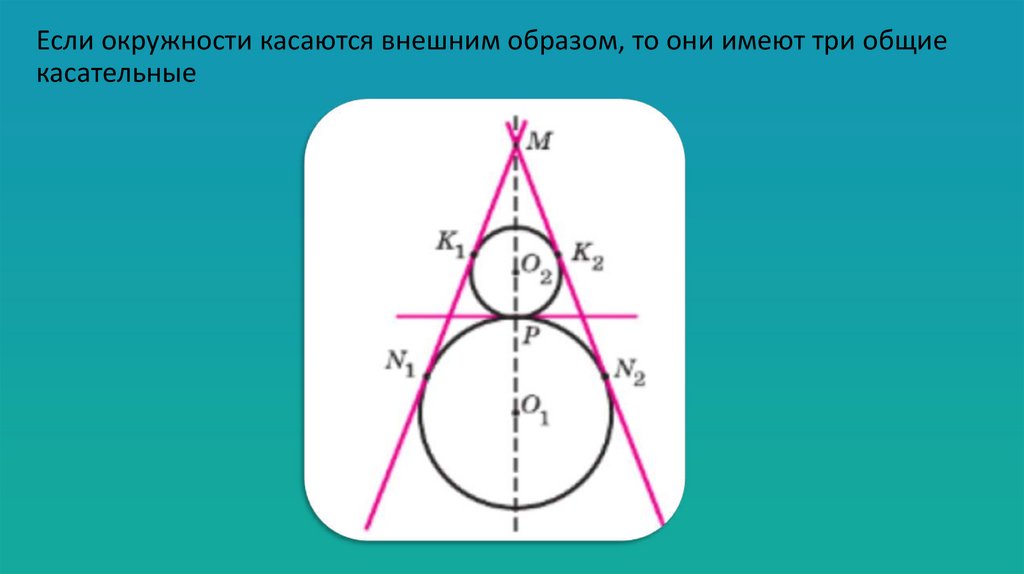
Если окружности касаются внешним образом, то они имеют три общие
касательные

13.

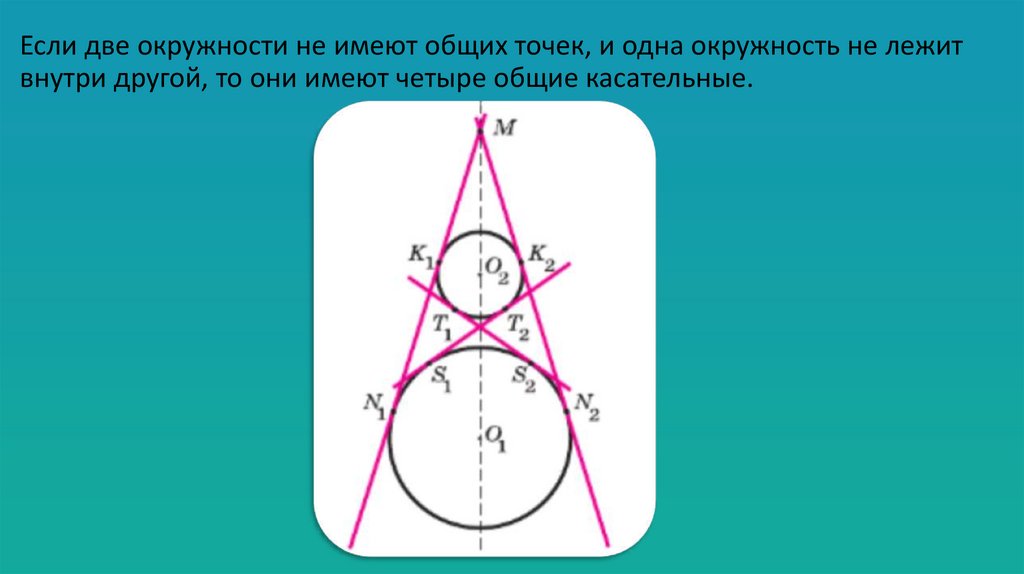
Если две окружности не имеют общих точек, и одна окружность не лежит
внутри другой, то они имеют четыре общие касательные.

14.

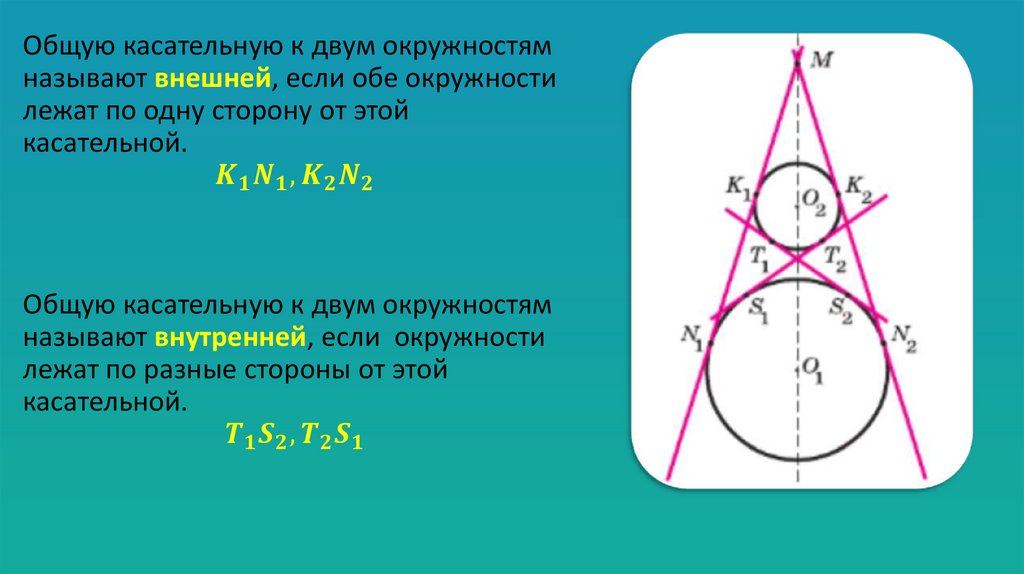
Общую касательную к двум окружностям
называют внешней, если обе окружности
лежат по одну сторону от этой
касательной.