Similar presentations:
Метод динамического программирования Р. Беллмана. Основное функциональное соотношение метода
1.
Тема 7.Метод динамического
программирования Р. Беллмана.
Основное функциональное соотношение
метода.
2.
Содержание1. Понятие многошагового процесса. Постановка задачи
оптимального управления многошаговым процессом. Принцип
оптимальности Р.Беллмана.
2. Метод динамического программирования, основное
функциональное соотношение метода. Прямая и обратная
прогонка.
3. Программное управление и управление с обратной связью
(синтез управления).
2
3. Задача оптимального управления
Оптимальное управление — это задача проектирования системы,обеспечивающей для заданного объекта управления или процесса
закон управления или управляющую последовательность
воздействий, обеспечивающих максимум или минимум заданной
совокупности критериев качества системы.
3
4. Метод динамического программирования Р. Беллмана
Метод динамического программирования – один из наиболееизвестных
математических
управления,
предложен
в
методов
конце
50-х
современной
годов
теории
американским
математиком Ричардом Беллманом.
4
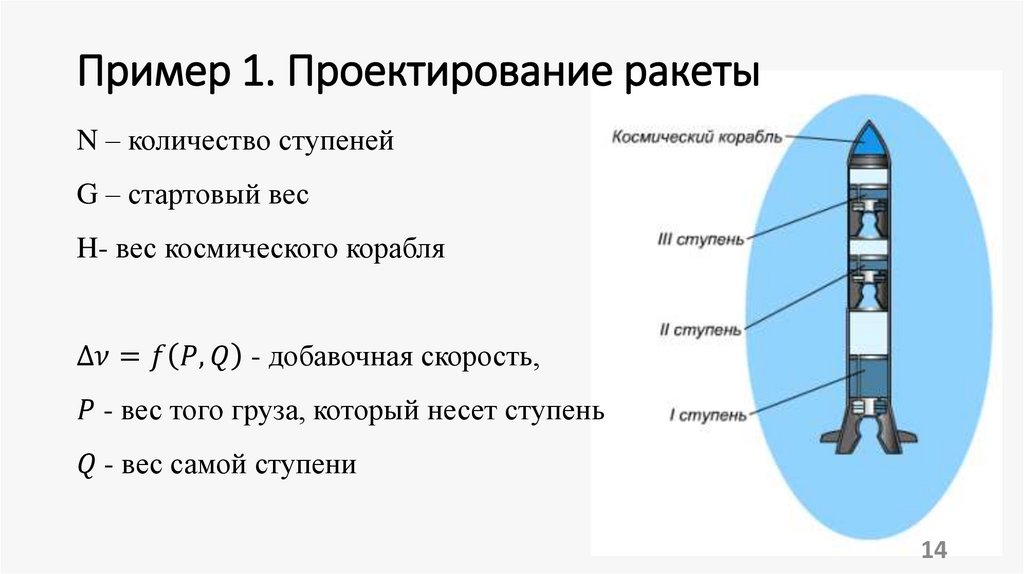
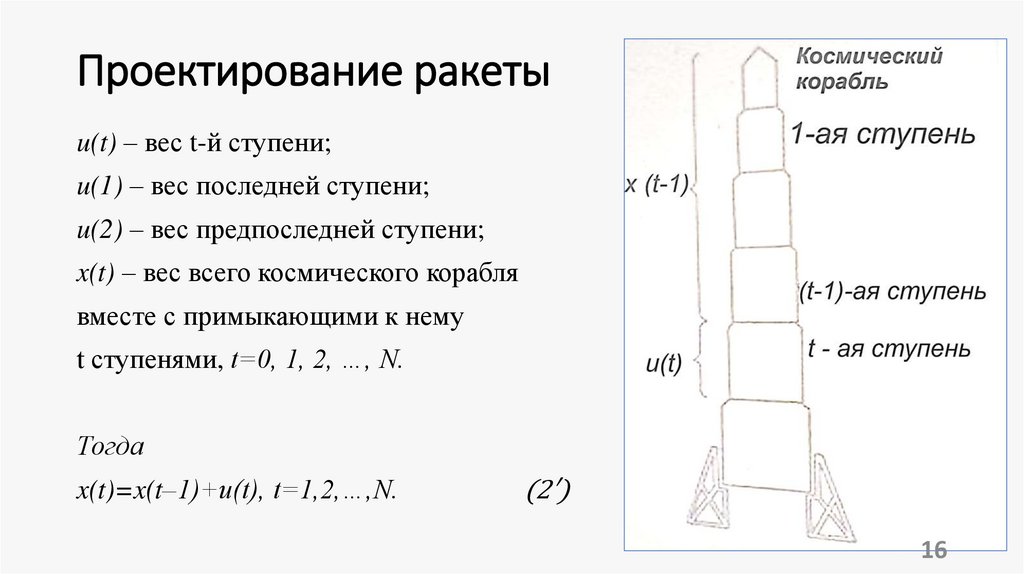
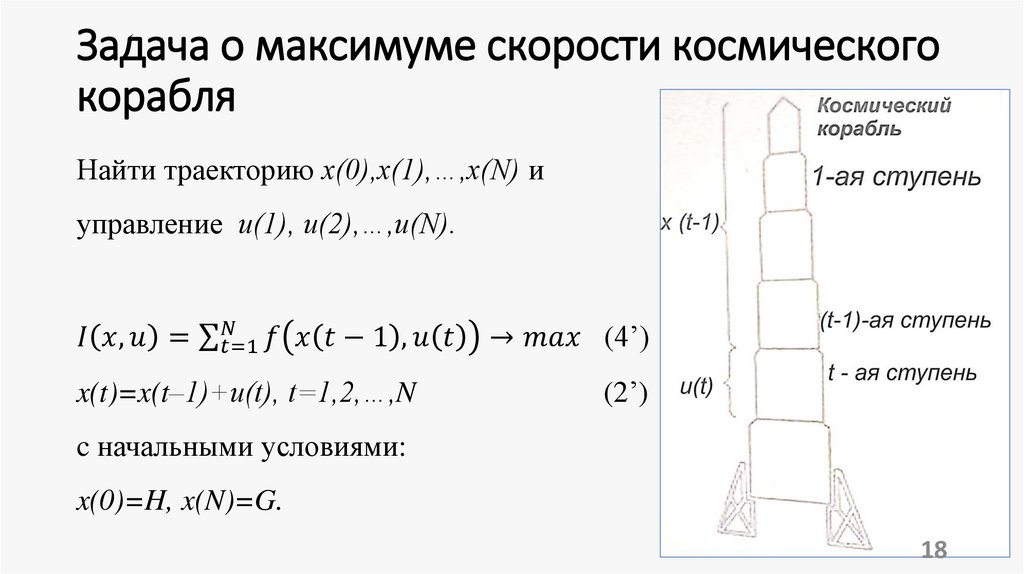
5. 1. Многошаговый процесс. Постановка задачи оптимального управления многошаговым процессом.
Рассматривается управляемая система.Пусть

























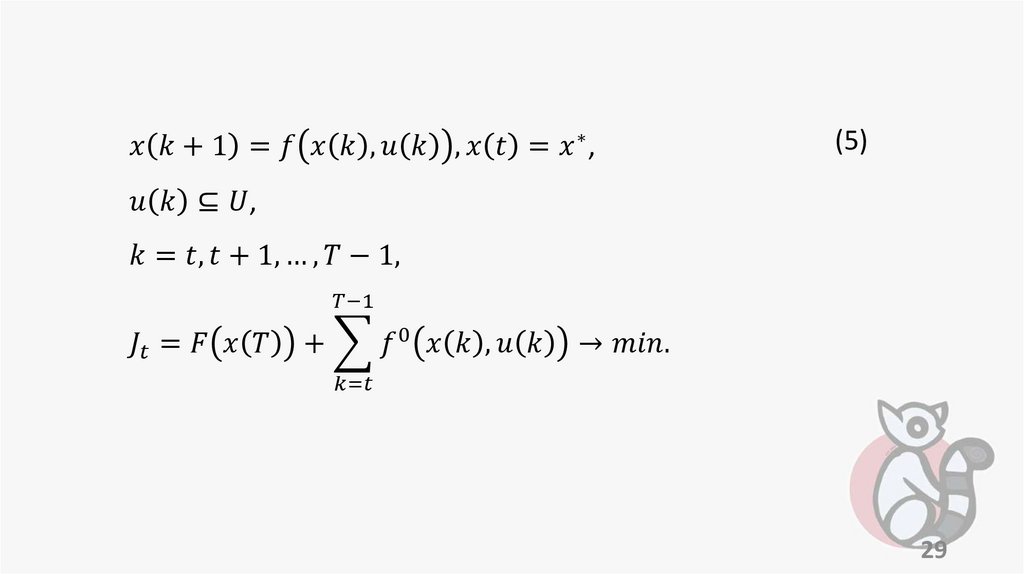
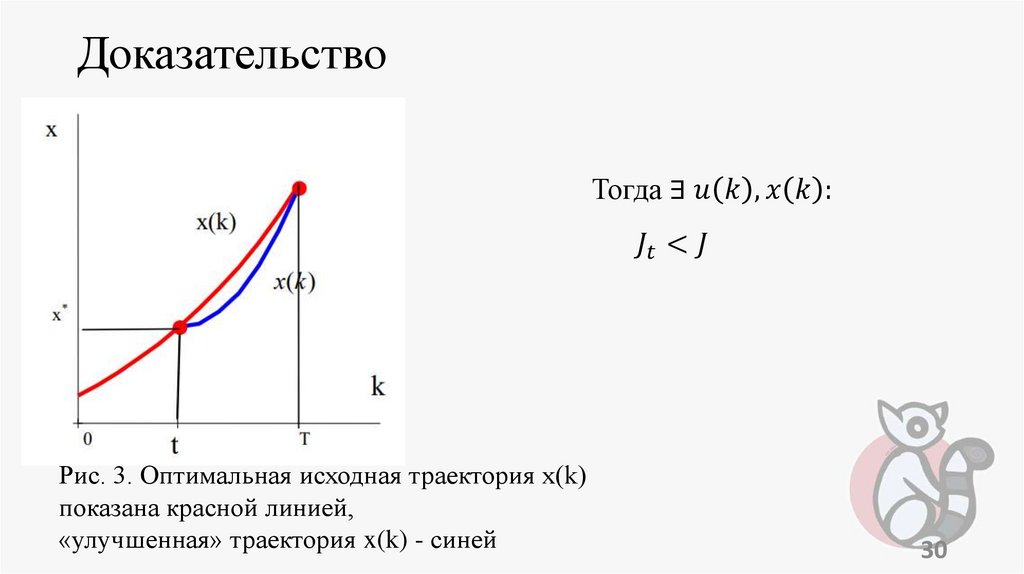
















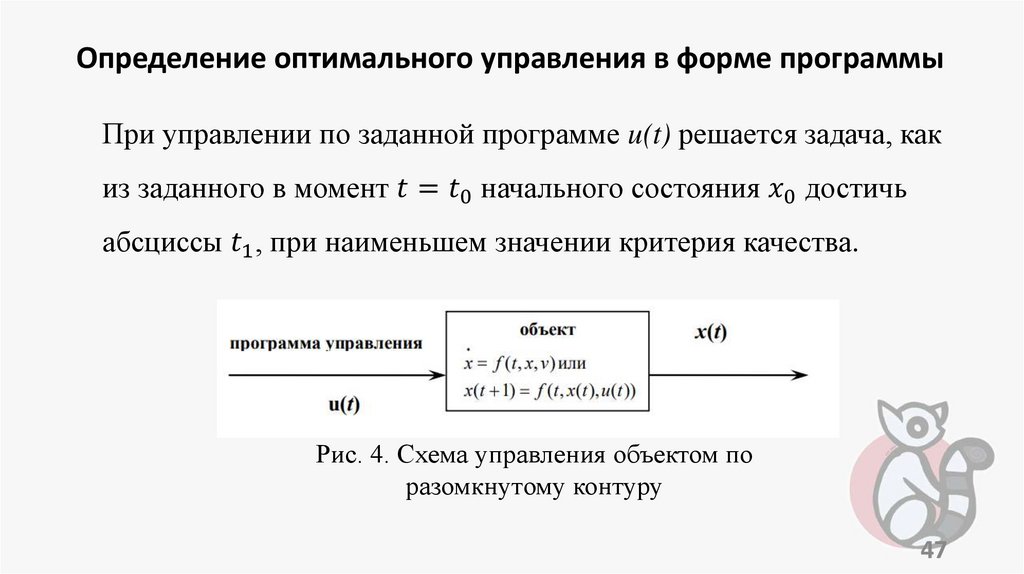
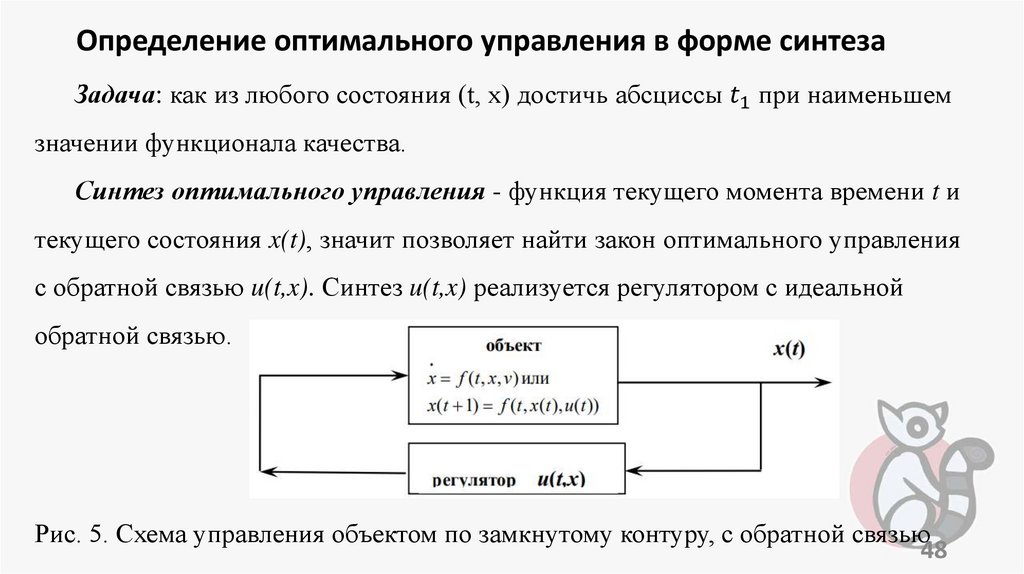







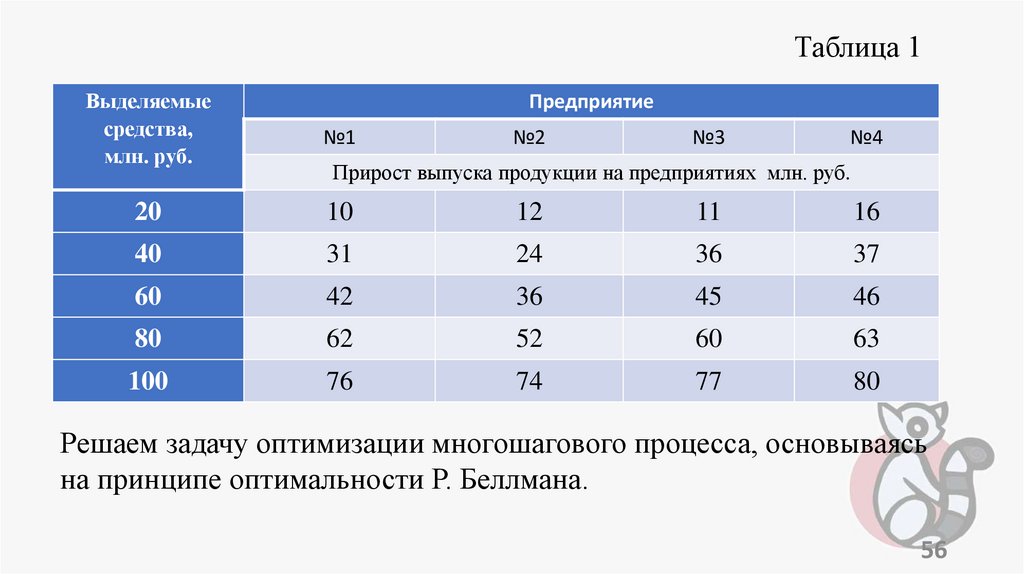
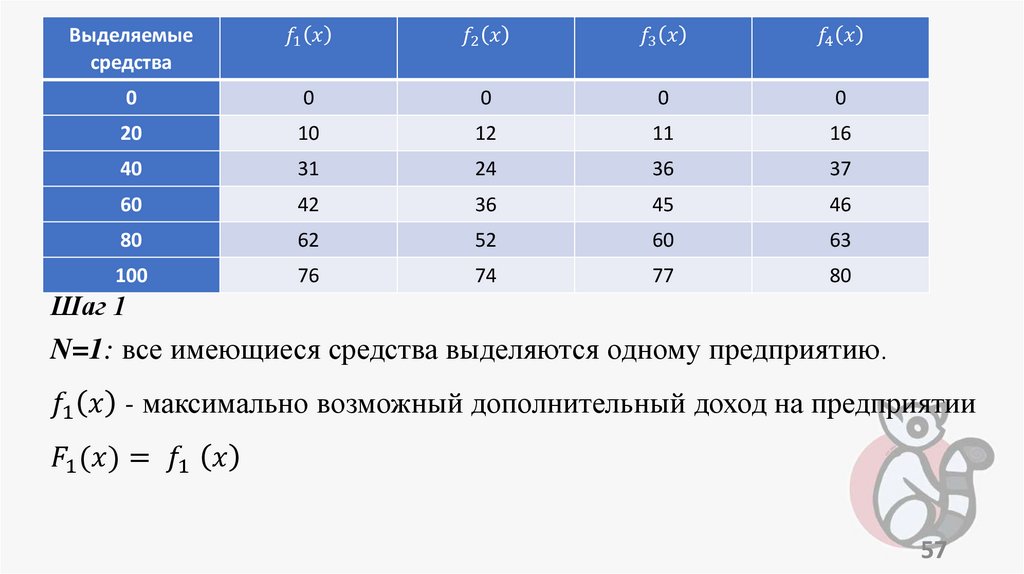

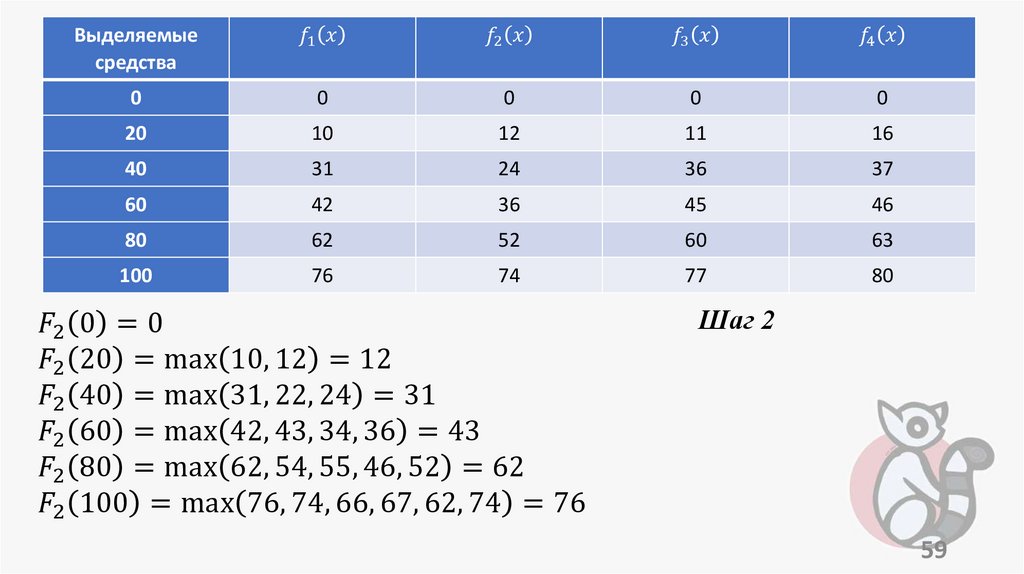
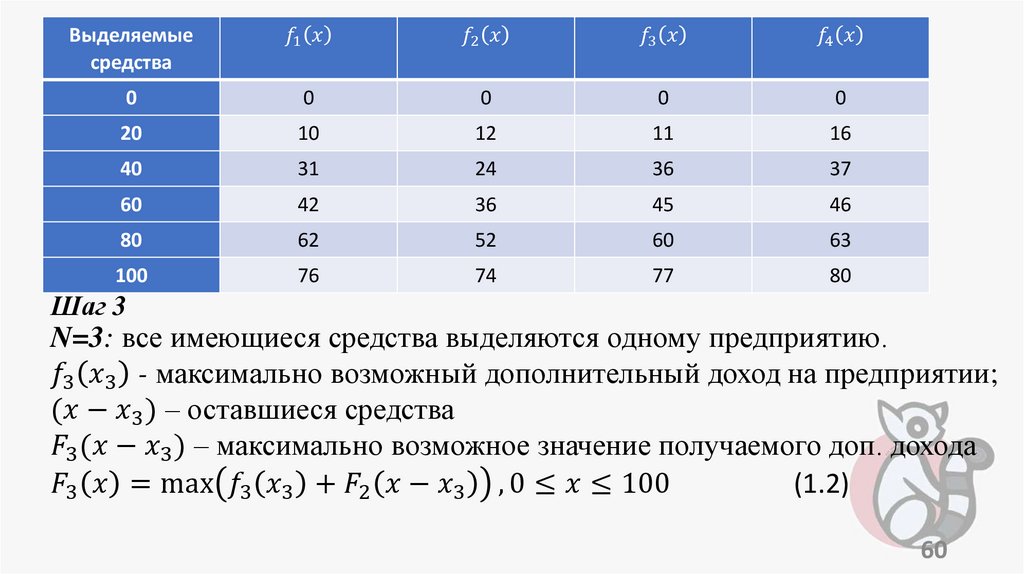


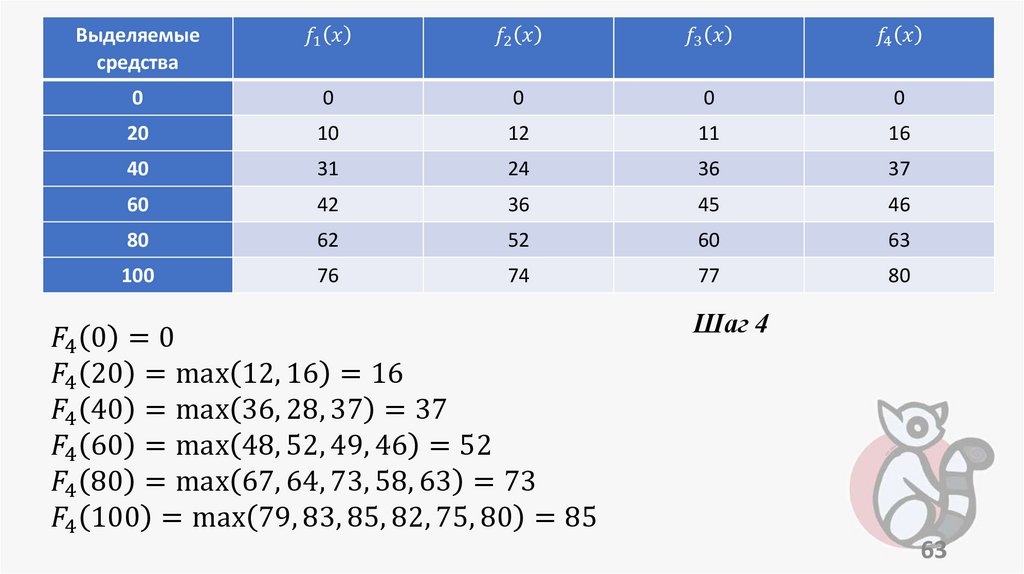
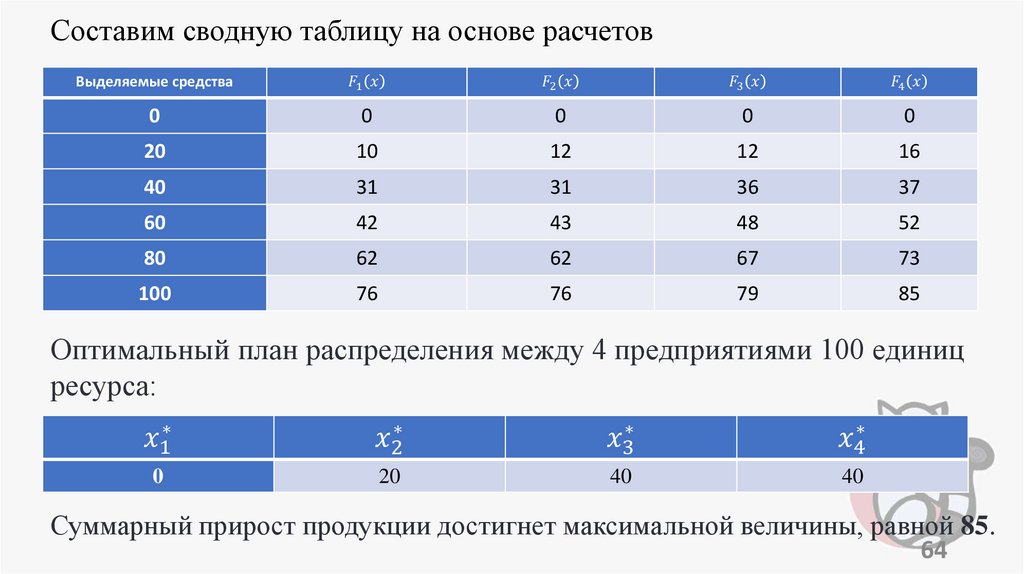







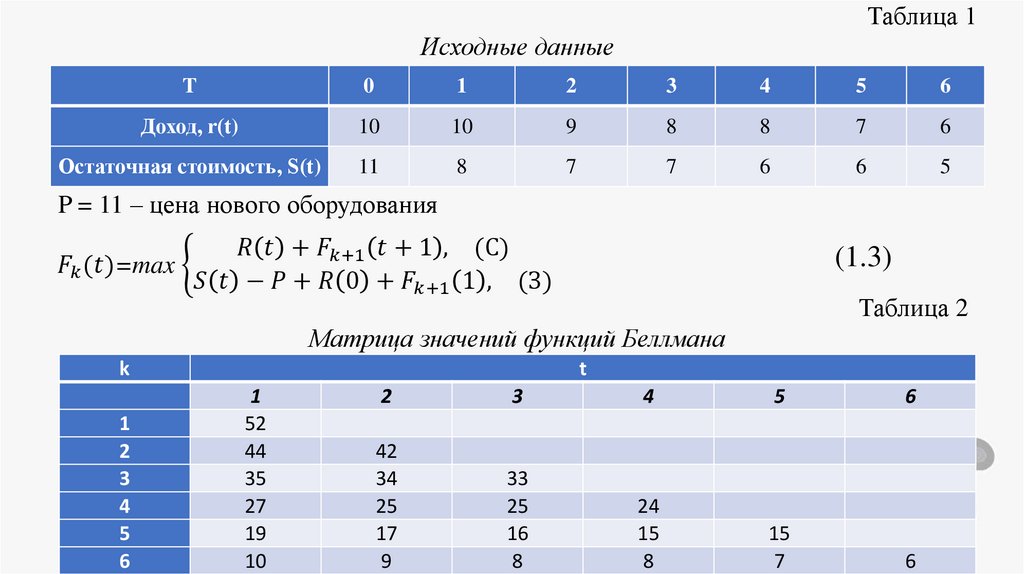

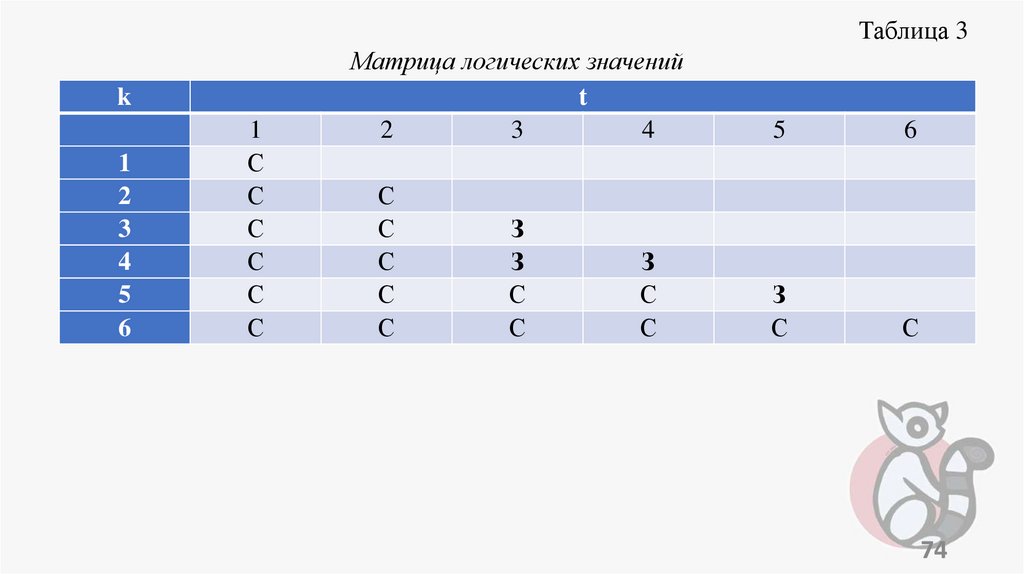

 programming
programming








