1.20M

Category:

informatics

Теория игр №19-21

пошагово разберём задачу на 1 кучу
19
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по
очереди, первый ход делает Петя. За один ход игрок может:
- добавить в кучу 3 камня;
- добавить в кучу 6 камней;
- увеличить количество камней в куче в 3 раза.
Например, из кучи в 20 камней за один ход можно получить кучу из 23, 26 или 60 камней.
Чтобы делать ходы, у каждого игрока есть неограниченное количество камней. Игра завершается в тот
момент, когда количество камней в куче становится не менее 132. Победителем считается игрок,
сделавший последний ход, т.е. первым получивший кучу из 132 или более камней. В начальный момент в
куче было S камней; 1 ≤ S ≤ 131.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах
противника.
Укажите минимальное значение S, при котором Петя не может выиграть за один ход, но при любом ходе
Пети Ваня может выиграть своим первым ходом.
python
excel
41
ответ

3.

пошагово разберём задачу на 1 кучу
20
Для игры, описанной в задании 19, найдите два наименьших значения S, при которых у Пети есть
выигрышная стратегия, причём одновременно выполняются два условия:
− Петя не может выиграть за один ход;
− Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Найденные значения запишите в ответе в порядке возрастания.
python
excel
ответ
14 35

4.

пошагово разберём задачу на 1 кучу
21
Для игры, описанной в задании 19, найдите минимальное значение S, при котором одновременно
выполняются два условия:
– у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой
игре Пети;
– у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
Если найдено несколько значений S, в ответе запишите наименьшее из них.
python
excel
ответ
32

5.

задача на 1 кучу:
19.
1
20.
1
21.
1

6.

пошагово разберём задачу на 2 кучи
19
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки
ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч (по
своему выбору) три камня или увеличить количество камней в куче в три раза. Для того чтобы
делать ходы, у каждого игрока есть неограниченное количество камней.
Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее
77. Победителем считается игрок, сделавший последний ход, т.е. первым получивший такую
позицию, при которой в кучах оказывается 77 или больше камней.
В начальный момент в первой куче было 12 камней, во второй куче – S камней; 1 ≤ S ≤ 64.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах
противника.
Укажите минимальное значение S, при котором Петя не может выиграть за один ход, но при любом
ходе Пети Ваня может выиграть своим первым ходом.
решение
21
ответ

7.

пошагово разберём задачу на 2 кучи
20
Для игры, описанной в задании 19, найдите два наименьших значения S, при которых у Пети есть
выигрышная стратегия, причём одновременно выполняются два условия:
– Петя не может выиграть за один ход;
– Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Найденные значения запишите в ответе в порядке возрастания.
решение
ответ
7 18

8.

пошагово разберём задачу на 2 кучи
21
Для игры, описанной в задании 19, найдите значения S, при которых одновременно выполняются два
условия:
– у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой
игре Пети;
– у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
В ответе укажите количество таких значений
решение
2
ответ

9.

уровень егэ:
19.
1
20.
1
21.
1
19.
2
20.
2
21.
2
19.
3
20.
3
21.
3
19.
4
20.
4
21.
4
сложные задачи:

10.

выбери своего бойца

11.

19
1) Сначала создаём две функции: step(p) - будет функцией шагов, на вход
будет подаваться куча камней, возвращаемое значение - это все возможные
ходы:
def step(p):
return p + 3, p + 6, p * 3
Во вторую функции записываем условие победы:
def step(p):
return p + 3, p + 6, p * 3
def win(p):
return p >= 132

12.

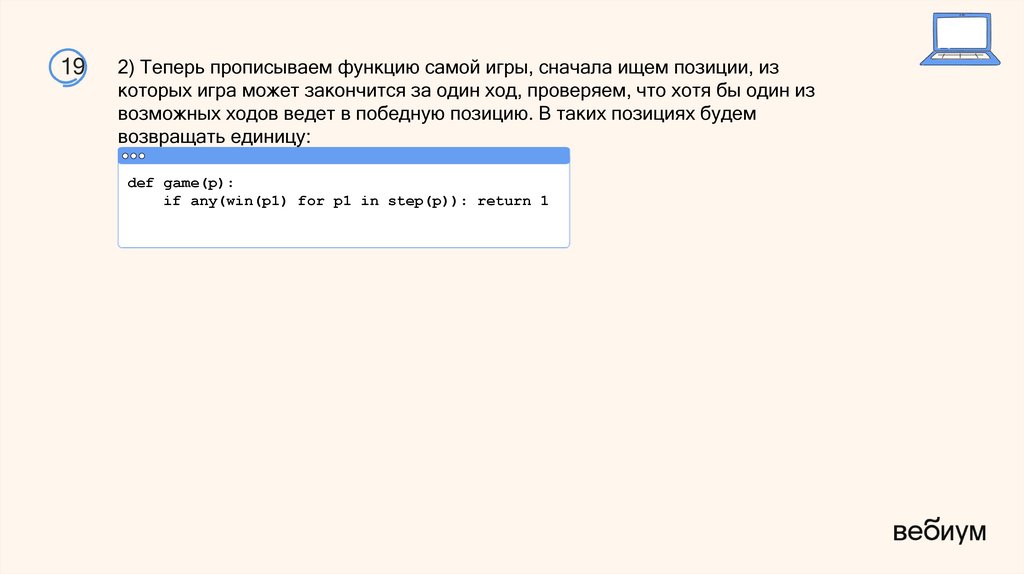
19
2) Теперь прописываем функцию самой игры, сначала ищем позиции, из
которых игра может закончится за один ход, проверяем, что хотя бы один из
возможных ходов ведет в победную позицию. В таких позициях будем
возвращать единицу:
def game(p):
if any(win(p1) for p1 in step(p)): return 1

13.

19
3) Теперь ищем позиции, из которых игра закончится за два хода, то есть
побеждает Ваня при любой игре Пети, через all проверяем, что все ходы ведут в
позиции с номером 1:
def step(p):
return p + 3, p + 6, p * 3
def win(p):
return p >= 132
def game(p):
if any(win(p1) for p1 in step(p)): return 1
if all(game(p2) == 1 for p2 in step(p)): return 2

14.

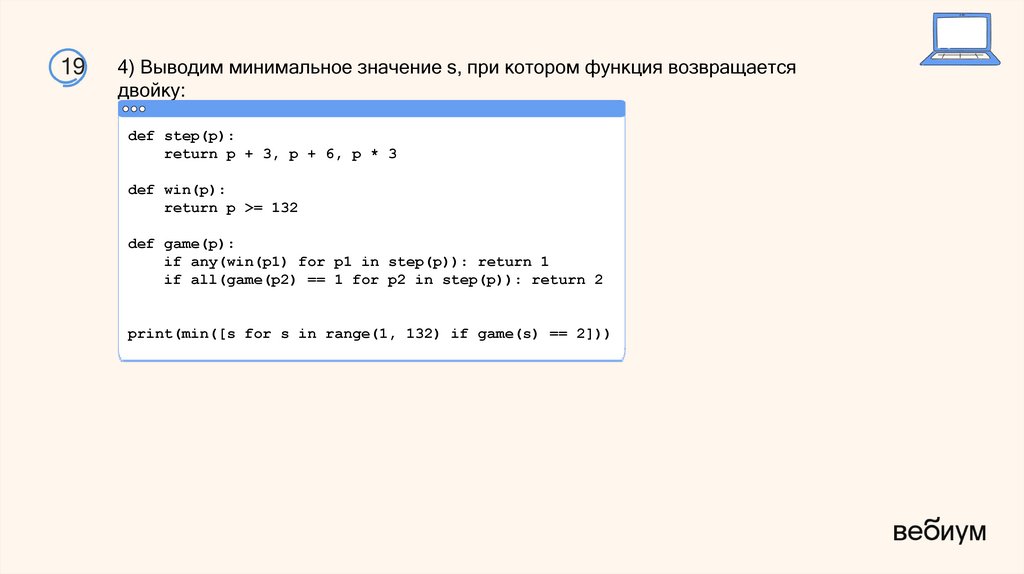
19
4) Выводим минимальное значение s, при котором функция возвращается
двойку:
def step(p):
return p + 3, p + 6, p * 3
def win(p):
return p >= 132
def game(p):
if any(win(p1) for p1 in step(p)): return 1
if all(game(p2) == 1 for p2 in step(p)): return 2
print(min([s for s in range(1, 132) if game(s) == 2]))

15.

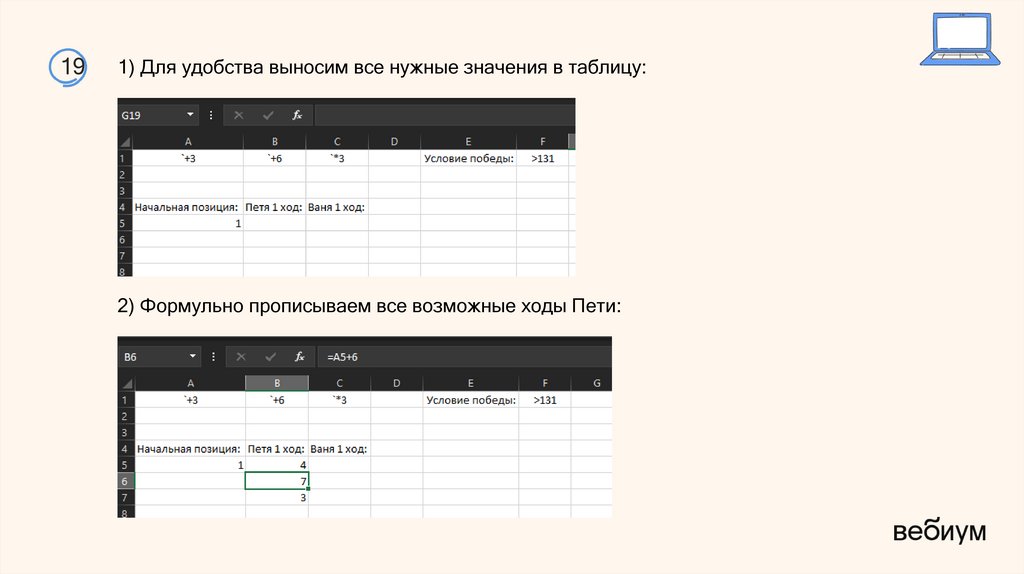
19
1) Для удобства выносим все нужные значения в таблицу:
2) Формульно прописываем все возможные ходы Пети:

16.

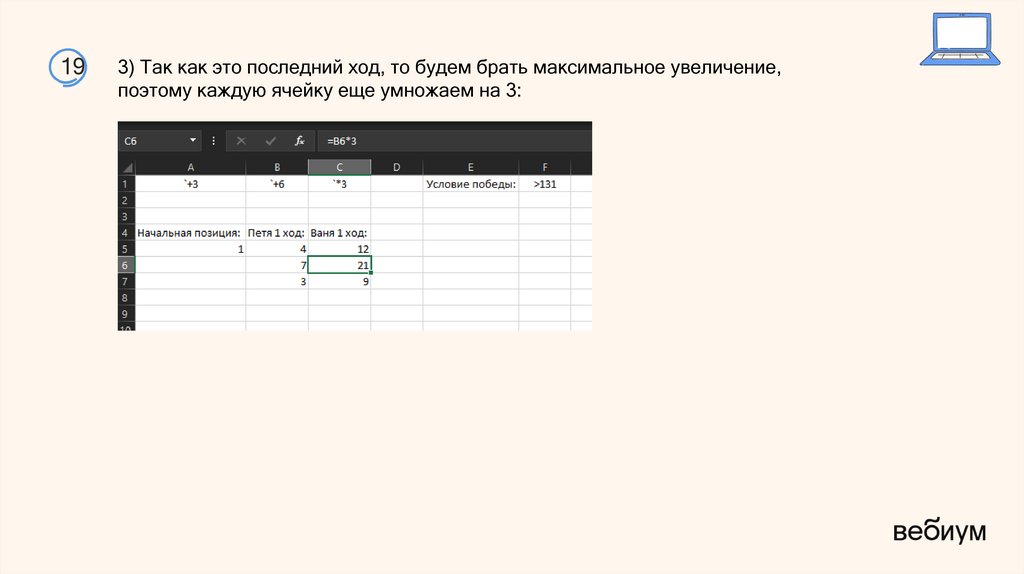
19
3) Так как это последний ход, то будем брать максимальное увеличение,
поэтому каждую ячейку еще умножаем на 3:

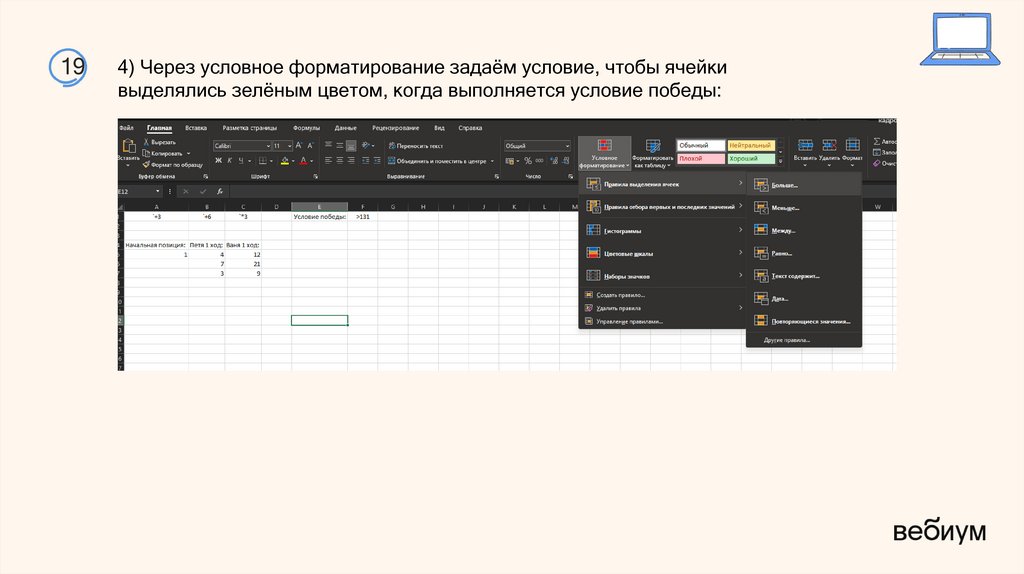
17.

19
4) Через условное форматирование задаём условие, чтобы ячейки
выделялись зелёным цветом, когда выполняется условие победы:

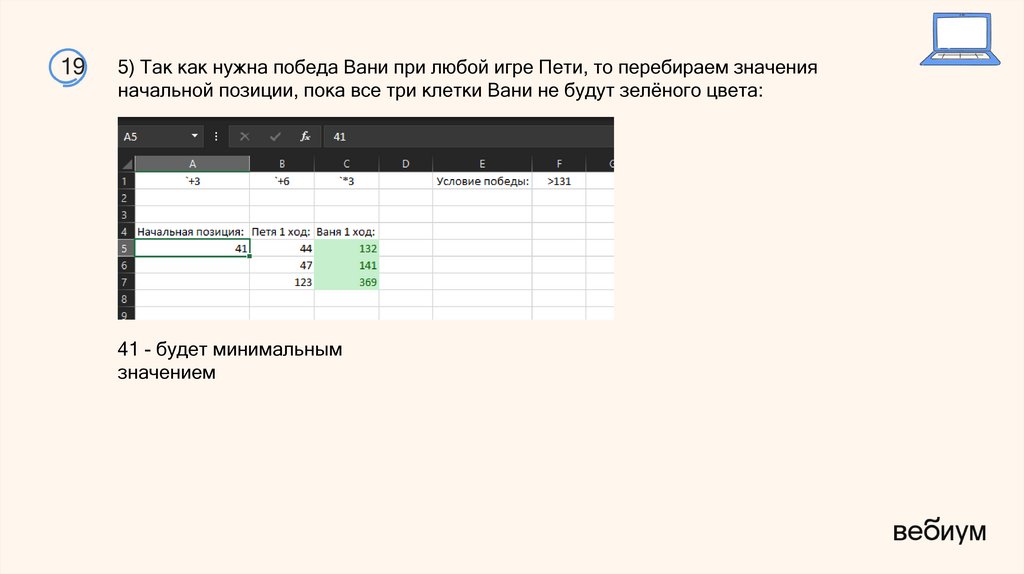
18.

19
5) Так как нужна победа Вани при любой игре Пети, то перебираем значения
начальной позиции, пока все три клетки Вани не будут зелёного цвета:
41 - будет минимальным
значением

19.

20
1) Петя должен победить своим вторым ходом, значит должна быть
ситуация, когда один из его ходов ведет в позицию с номером два,
ищем такие ситуации:
def step(p):
return p + 3, p + 6, p * 3
def win(p):
return p >= 132
def game(p):
if any(win(p1) for p1 in step(p)): return 1
if all(game(p2) == 1 for p2 in step(p)): return 2
if any(game(p3) == 2 for p3 in step(p)): return 3
Получается, что Петя ходит в позицию с номером 2, от туда Ваня всегда
попадает в позиции с номером 1, из которых Петя побеждает вторым
ходом.

20.

20
2) Выводим два минимальных значения:
def step(p):
return p + 3, p + 6, p * 3
def win(p):
return p >= 132
def game(p):
if any(win(p1) for p1 in step(p)): return 1
if all(game(p2) == 1 for p2 in step(p)): return 2
if any(game(p3) == 2 for p3 in step(p)): return 3
print([s for s in range(1, 132) if game(s) == 3][:2])

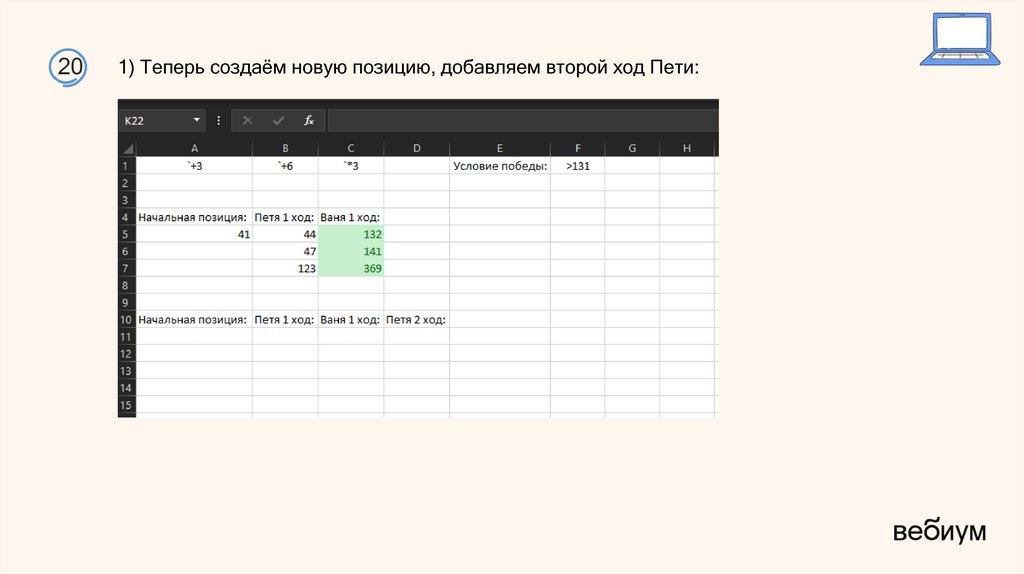
21.

20
1) Теперь создаём новую позицию, добавляем второй ход Пети:

22.

20
2) В качестве таблиц скопируем первую три раза:
Будем рассматривать все возможные ходы Пети, из которых Ваня будет
делать свои все возможные ходы, из которых Петя будет делать
максимальное увеличение.

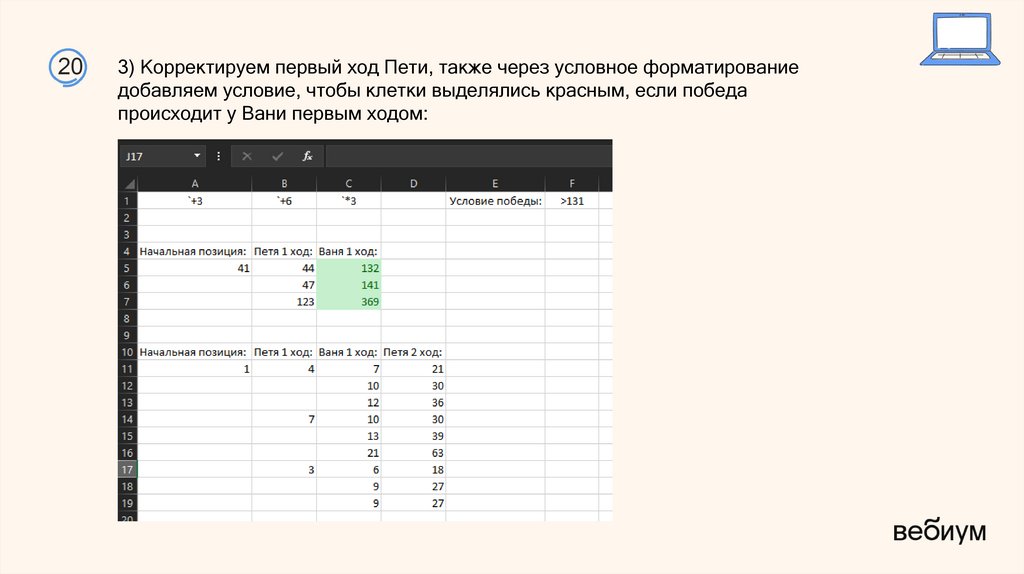
23.

20
3) Корректируем первый ход Пети, также через условное форматирование
добавляем условие, чтобы клетки выделялись красным, если победа
происходит у Вани первым ходом:

24.

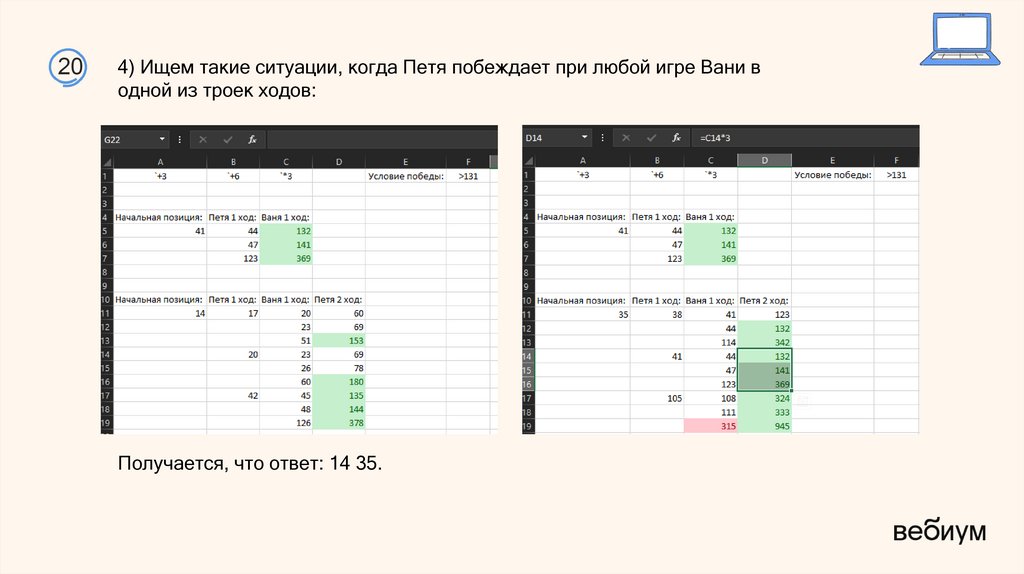
20
4) Ищем такие ситуации, когда Петя побеждает при любой игре Вани в
одной из троек ходов:
Получается, что ответ: 14 35.

25.

21
1) Ваня побеждает либо первым, либо вторым ходом, получается, что
все ходы Пети должны вести либо в позиции с номером 1, либо 3:
def step(p):
return p + 3, p + 6, p * 3
def win(p):
return p >= 132
def game(p):
if any(win(p1) for p1 in step(p)): return 1
if all(game(p2) == 1 for p2 in step(p)): return 2
if any(game(p3) == 2 for p3 in step(p)): return 3
if all(game(p4) in (1,3) for p4 in step(p)): return 4

26.

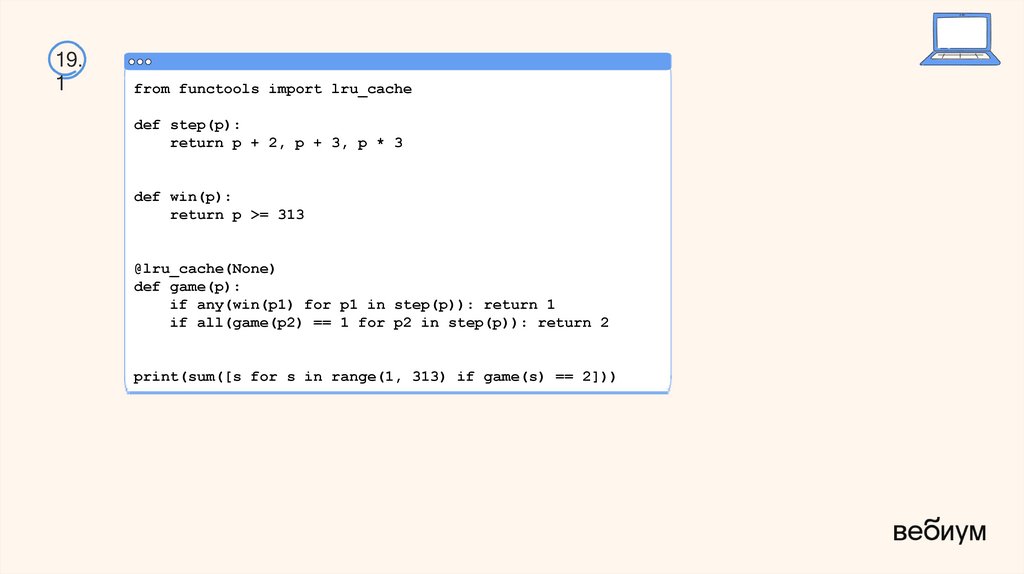
21
2) Выводим минимальное значение, также можно добавить модуль
lru_cache, чтобы ускорить функцию:
from functools import lru_cache
def step(p):
return p + 3, p + 6, p * 3
def win(p):
return p >= 132
@lru_cache(None)
def game(p):
if any(win(p1) for p1 in step(p)): return 1
if all(game(p2) == 1 for p2 in step(p)): return 2
if any(game(p3) == 2 for p3 in step(p)): return 3
if all(game(p4) in (1, 3) for p4 in step(p)): return 4
print(min([s for s in range(1, 132) if game(s) == 4]))

27.

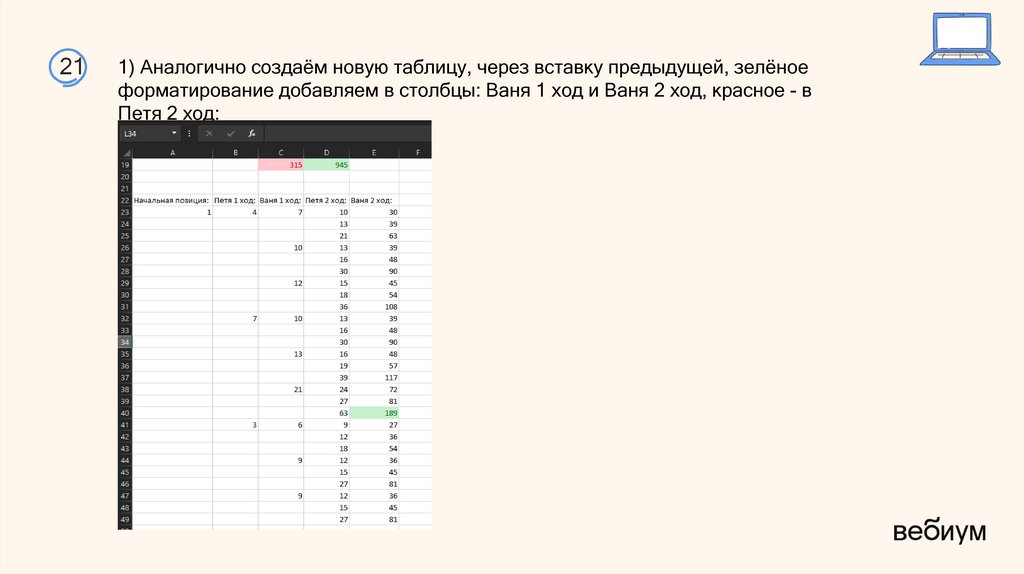
21
1) Аналогично создаём новую таблицу, через вставку предыдущей, зелёное
форматирование добавляем в столбцы: Ваня 1 ход и Ваня 2 ход, красное - в
Петя 2 ход:

28.

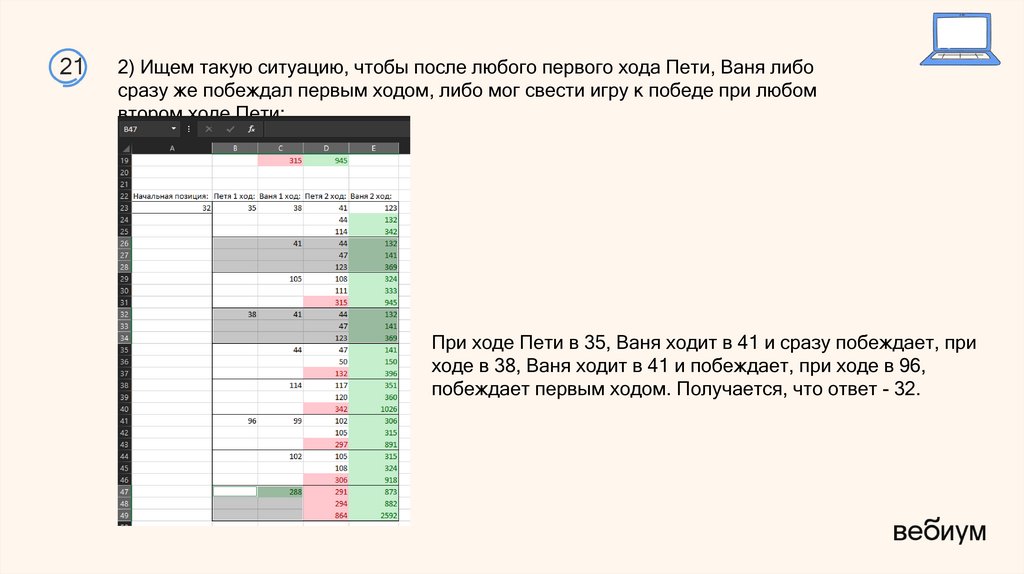
21
2) Ищем такую ситуацию, чтобы после любого первого хода Пети, Ваня либо
сразу же побеждал первым ходом, либо мог свести игру к победе при любом
втором ходе Пети:
При ходе Пети в 35, Ваня ходит в 41 и сразу побеждает, при
ходе в 38, Ваня ходит в 41 и побеждает, при ходе в 96,
побеждает первым ходом. Получается, что ответ - 32.

29.

19
1) Прописываем функцию шагов:
def step(p):
(a, b) = p
return (a + 3, b), (a, b + 3), (a * 3, b), (a, b * 3)

30.

19
2) Прописываем условие на победу:
def step(p):
(a, b) = p
return (a + 3, b), (a, b + 3), (a * 3, b), (a, b * 3)
def win(p):
return sum(p) >= 77

31.

19
3) Прописываем функцию игры аналогично одной куче, позиции из
которых игра кончается за 1 ход, позиции, которые всегда ведут в
позиции с номером один:
def step(p):
(a, b) = p
return (a + 3, b), (a, b + 3), (a * 3, b), (a, b * 3)
def win(p):
return sum(p) >= 77
def game(p):
if any(win(p1) for p1 in step(p)): return 1
if all(game(p2) == 1 for p2 in step(p)): return 2

32.

19
4) Выводим нужные значения:
def step(p):
(a, b) = p
return (a + 3, b), (a, b + 3), (a * 3, b), (a, b * 3)
def win(p):
return sum(p) >= 77
def game(p):
if any(win(p1) for p1 in step(p)): return 1
if all(game(p2) == 1 for p2 in step(p)): return 2
print(min([s for s in range(1, 65) if game((12, s)) == 2]))

33.

20
Ищем позиции, из которых есть ход в позицию с номером два,
выводим нужные значения:
def step(p):
(a, b) = p
return (a + 3, b), (a, b + 3), (a * 3, b), (a, b * 3)
def win(p):
return sum(p) >= 77
def game(p):
if any(win(p1) for p1 in step(p)): return 1
if all(game(p2) == 1 for p2 in step(p)): return 2
if any(game(p3) == 2 for p3 in step(p)): return 3
print([s for s in range(1, 65) if game((12, s)) == 3][:2])

34.

21
Ищем позиции из которых Ваня побеждает либо, первым, либо вторым
ходом, выводим нужное значение:
def step(p):
(a, b) = p
return (a + 3, b), (a, b + 3), (a * 3, b), (a, b * 3)
def win(p):
return sum(p) >= 77
def game(p):
if any(win(p1) for p1 in step(p)): return 1
if all(game(p2) == 1 for p2 in step(p)): return 2
if any(game(p3) == 2 for p3 in step(p)): return 3
if all(game(p4) in (1, 3) for p4 in step(p)): return 4
print(len([s for s in range(1, 65) if game((12, s)) == 4]))

35.

19.
1
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней.
Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в
кучу 2 или 3 камня либо увеличить количество камней в куче в 3 раза. Для того, чтобы
делать ходы, у каждого игрока есть неограниченное количество камней.
Игра завершается в тот момент, когда количество камней в куче становится не менее 313.
Победителем считается игрок, сделавший последний ход, т.е. первым получивший кучу,
состоящую из 313 или более камней.
В начальный момент в куче было S камней; 1 ≤ S ≤ 312.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при
любых ходах противника.
Укажите сумму таких значений S, при которых Петя не может выиграть за один ход, но при
любом ходе Пети Ваня может выиграть своим первым ходом.
пояснение
ответ
207

36.

19.
1
from functools import lru_cache
def step(p):
return p + 2, p + 3, p * 3
def win(p):
return p >= 313
@lru_cache(None)
def game(p):
if any(win(p1) for p1 in step(p)): return 1
if all(game(p2) == 1 for p2 in step(p)): return 2
print(sum([s for s in range(1, 313) if game(s) == 2]))

37.

20.
1
Для игры, описанной в задании 19.1, найдите наименьшее и наибольшее значения S, при
которых у Пети есть выигрышная стратегия, причём одновременно выполняются два
условия:
− Петя не может выиграть за один ход;
− Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Найденные значения запишите в ответе в порядке возрастания.
пояснение
100 102
ответ

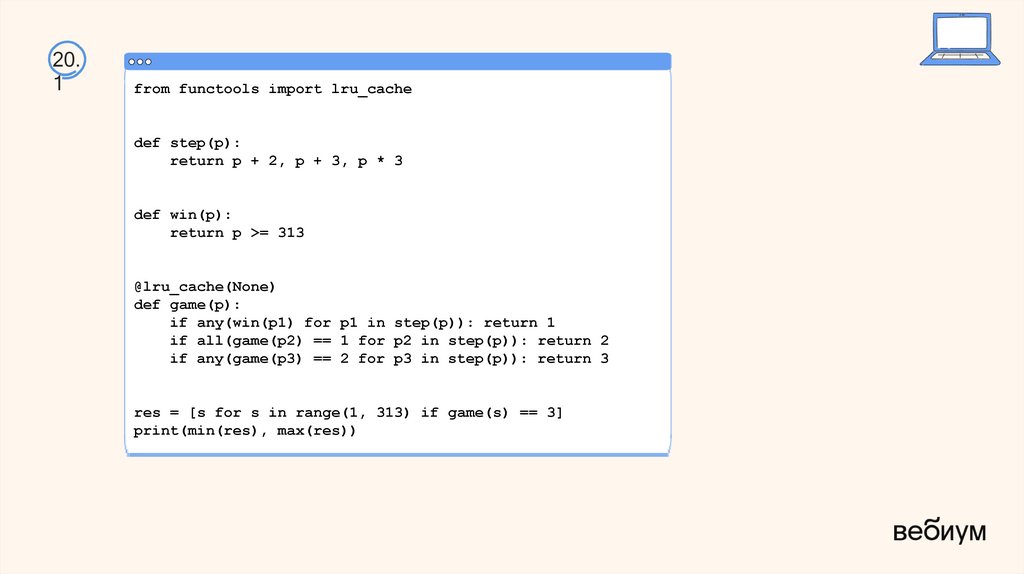
38.

20.
1
from functools import lru_cache
def step(p):
return p + 2, p + 3, p * 3
def win(p):
return p >= 313
@lru_cache(None)
def game(p):
if any(win(p1) for p1 in step(p)): return 1
if all(game(p2) == 1 for p2 in step(p)): return 2
if any(game(p3) == 2 for p3 in step(p)): return 3
res = [s for s in range(1, 313) if game(s) == 3]
print(min(res), max(res))

39.

21.
1
Для игры, описанной в задании 19.1, найдите сумму таких значений S, при которых
одновременно выполняются два условия:
– у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым
ходом при любой игре Пети;
– у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
пояснение
197
ответ

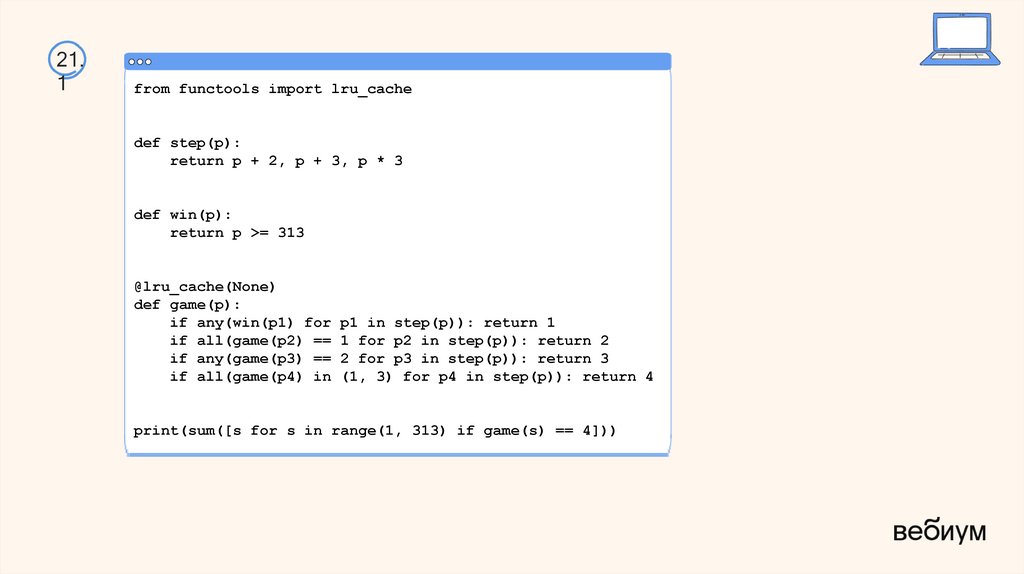
40.

21.
1
from functools import lru_cache
def step(p):
return p + 2, p + 3, p * 3
def win(p):
return p >= 313
@lru_cache(None)
def game(p):
if any(win(p1) for p1 in step(p)): return 1
if all(game(p2) == 1 for p2 in step(p)): return 2
if any(game(p3) == 2 for p3 in step(p)): return 3
if all(game(p4) in (1, 3) for p4 in step(p)): return 4
print(sum([s for s in range(1, 313) if game(s) == 4]))

41.

19.
1
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи
камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может
добавить в одну из куч (по своему выбору) десять камней или увеличить количество
камней в куче в два раза. Для того чтобы делать ходы, у каждого игрока есть
неограниченное количество камней.
Игра завершается в тот момент, когда произведение количеств камней в кучах становится
не менее 541. Победителем считается игрок, сделавший последний ход, т.е. первым
получивший такую позицию, при которой произведение количества камней в кучах будет
больше либо равно 541.
В начальный момент в первой куче было 6 камней, во второй куче – S камней; 1 ≤ S ≤ 90.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при
любых ходах противника.
Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети.
Укажите минимальное значение S, когда такая ситуация возможна.
пояснение
17
ответ

42.

19.
1
def step(p):
(a, b) = p
return (a + 10, b), (a, b + 10), (a * 2, b), (a, b * 2)
def win(p):
return p[0] * p[1] >= 541
def game(p):
if any(win(p1) for p1 in step(p)): return 1
if any(game(p2) == 1 for p2 in step(p)): return 2
print(min([s for s in range(1, 91) if game((6, s)) == 2]))
Если просят рассмотреть неудачный ход Пети, значит нужно найти такие позиции, из
которых есть хотя бы один ход в позицию с номером 1, его и совершит Петя. Меняем all на
any.

43.

20.
1
Для игры, описанной в предыдущем задании, найдите наименьшее и наибольшее
значения S, при которых у Пети есть выигрышная стратегия, причём одновременно
выполняются два условия:
− Петя не может выиграть за один ход;
− Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Найденные значения запишите в ответе в порядке возрастания.
пояснение
ответ
11 23

44.

20.
1
def step(p):
(a, b) = p
return (a + 10, b), (a, b + 10), (a * 2, b), (a, b * 2)
def win(p):
return p[0] * p[1] >= 541
def game(p):
if any(win(p1) for p1 in step(p)): return 1
if all(game(p2) == 1 for p2 in step(p)): return 2
if any(game(p3) == 2 for p3 in step(p)): return 3
res = [s for s in range(1, 91) if game((6, s)) == 3]
print(min(res), max(res))

45.

21.
1
Для игры, описанной в задании 19.1, найдите минимальное значение S, при котором
одновременно выполняются два условия:
– у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым
ходом при любой игре Пети;
– у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
пояснение
ответ
6

46.

21.
1
def step(p):
(a, b) = p
return (a + 10, b), (a, b + 10), (a * 2, b), (a, b * 2)
def win(p):
return p[0] * p[1] >= 541
def game(p):
if any(win(p1) for p1 in step(p)): return 1
if all(game(p2) == 1 for p2 in step(p)): return 2
if any(game(p3) == 2 for p3 in step(p)): return 3
if all(game(p4) in (1, 3) for p4 in step(p)): return 4
print(min([s for s in range(1, 91) if game((6, s)) == 4]))

47.

19.
2
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней.
Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может убрать из одной
из куч два камня или уменьшить количество камней в куче в два раза (если количество
камней в куче нечётно, остаётся на 1 камень больше, чем убирается). Например, пусть в
одной куче 6, а в другой 9 камней; такую позицию мы будем обозначать (6, 9). За один ход из
позиции (6, 9) можно получить любую из трёх позиций: (3, 9), (6, 7), (4, 9) и (6, 5).
Игра завершается в тот момент, когда суммарное количество камней в кучах становится не
более 108. Победителем считается игрок, сделавший последний ход, то есть первым
получивший позицию, в которой в кучах будет 108 или меньше камней.
В начальный момент в первой куче было 60 камней, во второй куче – S камней, S > 48.
Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети.
Укажите максимальное значение S, когда такая ситуация возможна.
пояснение
ответ
192

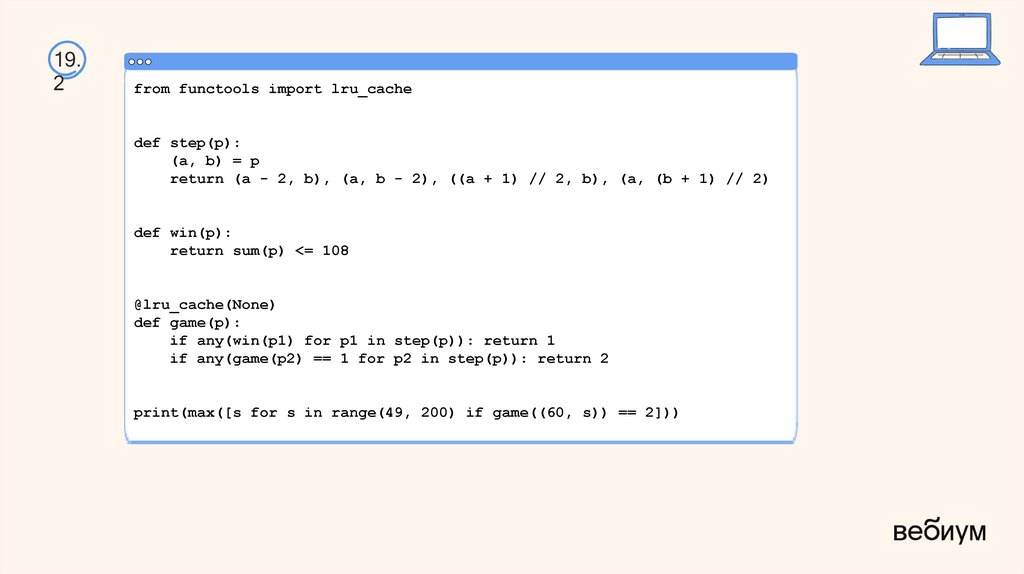
48.

19.
2
from functools import lru_cache
def step(p):
(a, b) = p
return (a - 2, b), (a, b - 2), ((a + 1) // 2, b), (a, (b + 1) // 2)
def win(p):
return sum(p) <= 108
@lru_cache(None)
def game(p):
if any(win(p1) for p1 in step(p)): return 1
if any(game(p2) == 1 for p2 in step(p)): return 2
print(max([s for s in range(49, 200) if game((60, s)) == 2]))

49.

20.
2
Для игры, описанной в задании 19.2, найдите минимальное и максимальное значения S, при
котором у Пети есть выигрышная стратегия, причём одновременно выполняются два
условия:
− Петя не может выиграть за один ход;
− Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Найденные значения запишите в ответе в порядке возрастания.
пояснение
ответ
99 196

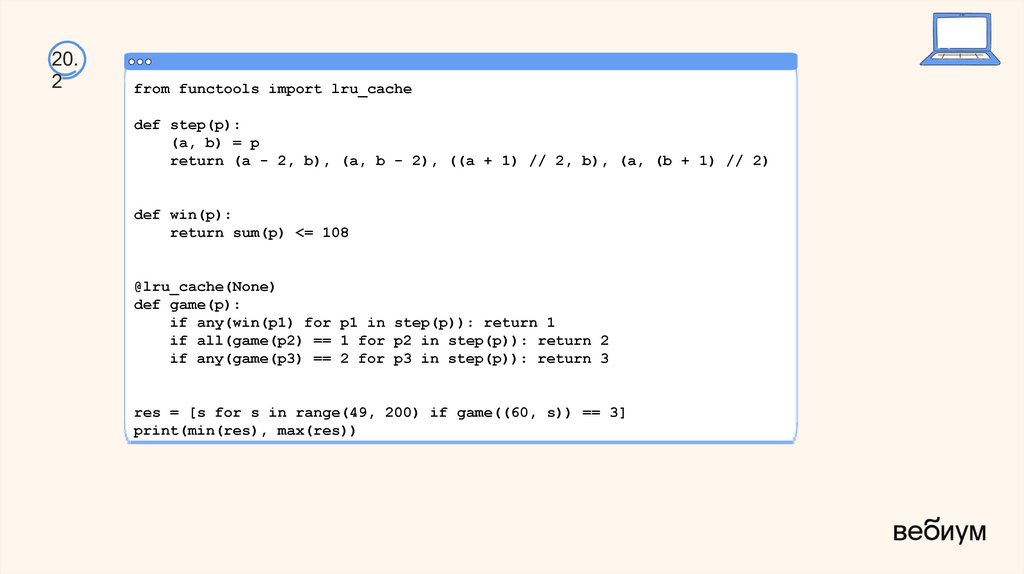
50.

20.
2
from functools import lru_cache
def step(p):
(a, b) = p
return (a - 2, b), (a, b - 2), ((a + 1) // 2, b), (a, (b + 1) // 2)
def win(p):
return sum(p) <= 108
@lru_cache(None)
def game(p):
if any(win(p1) for p1 in step(p)): return 1
if all(game(p2) == 1 for p2 in step(p)): return 2
if any(game(p3) == 2 for p3 in step(p)): return 3
res = [s for s in range(49, 200) if game((60, s)) == 3]
print(min(res), max(res))

51.

21.
2
Для игры, описанной в задании 19.2, найдите наибольшее значение S, при котором
одновременно выполняются два условия:
– у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом
при любой игре Пети;
– у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
пояснение
ответ
160

52.

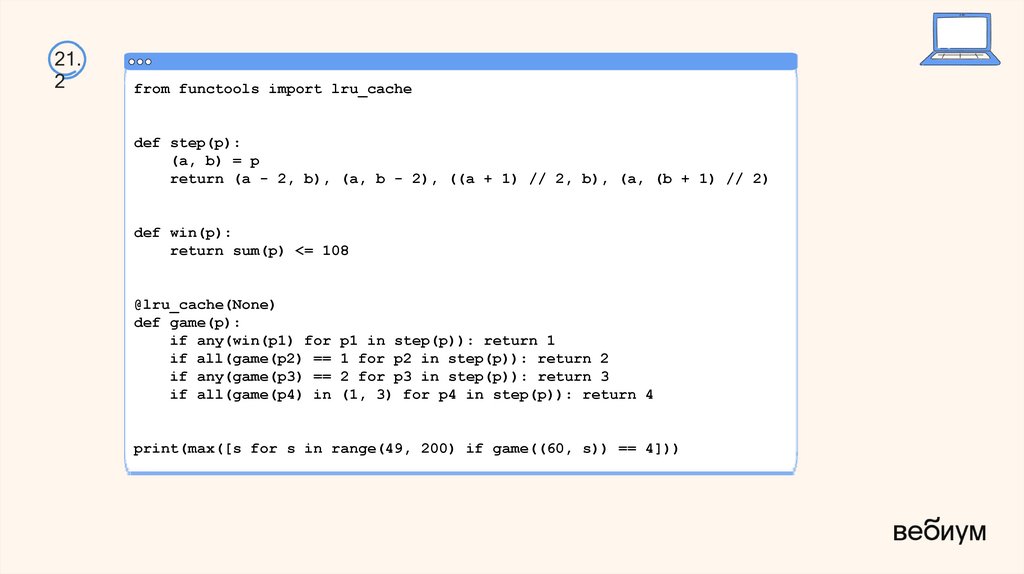
21.
2
from functools import lru_cache
def step(p):
(a, b) = p
return (a - 2, b), (a, b - 2), ((a + 1) // 2, b), (a, (b + 1) // 2)
def win(p):
return sum(p) <= 108
@lru_cache(None)
def game(p):
if any(win(p1) for p1 in step(p)): return 1
if all(game(p2) == 1 for p2 in step(p)): return 2
if any(game(p3) == 2 for p3 in step(p)): return 3
if all(game(p4) in (1, 3) for p4 in step(p)): return 4
print(max([s for s in range(49, 200) if game((60, s)) == 4]))

53.

19.
3
Два игрока, Папа и Ваня, играют в следующую игру. Перед игроками лежит куча камней.
Игроки ходят по очереди, первый ход делает Папа. За один ход игрок может добавить в кучу
семь камней или увеличить количество камней в куче в два раза. Для того чтобы делать
ходы, у каждого игрока есть неограниченное количество камней.
Игра завершается в тот момент, когда количество камней в куче становится не менее 100.
Победителем считается игрок, сделавший последний ход, т.е. первым получивший кучу из
100 или больше камней. В начальный момент в куче было S камней, 1 ≤ S ≤ 99.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых
ходах противника.
Укажите максимальное значение S, при котором Папа может выиграть своим первым ходом,
но поддается и Ваня выигрывает своим первым ходом.
пояснение
ответ
92

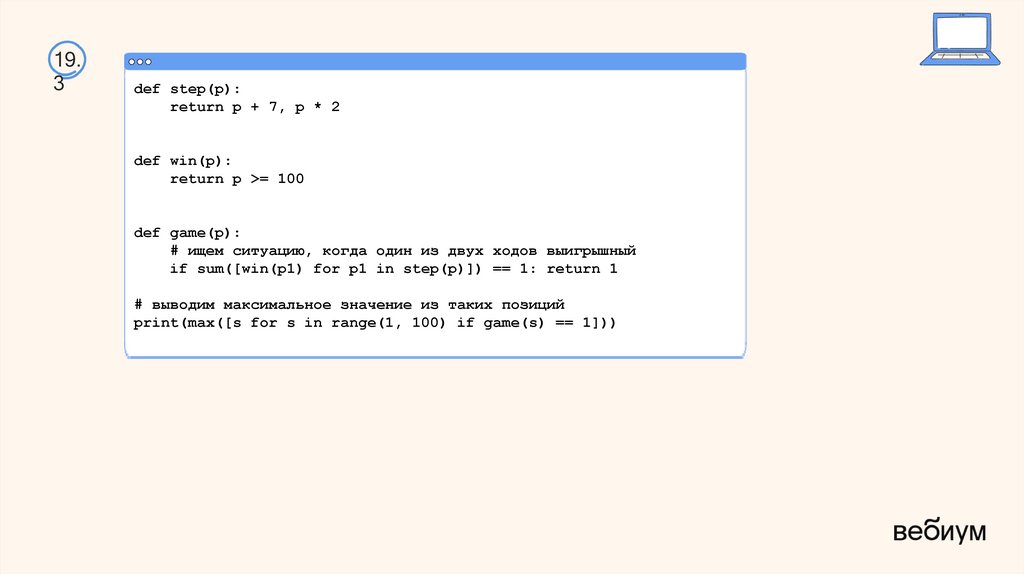
54.

19.
3
def step(p):
return p + 7, p * 2
def win(p):
return p >= 100
def game(p):
# ищем ситуацию, когда один из двух ходов выигрышный
if sum([win(p1) for p1 in step(p)]) == 1: return 1
# выводим максимальное значение из таких позиций
print(max([s for s in range(1, 100) if game(s) == 1]))

55.

20.
3
Для игры, описанной в задании 19.3, найдите два наименьших значения S, при которых у
Папы нет выигрышной стратегии. При этом, Ваня может выиграть своим первым ходом, но
ошибается, и Папа, не имея возможности поддаться, вынужден выиграть.
Найденные значения запишите в ответе в порядке возрастания.
пояснение
ответ
43 44

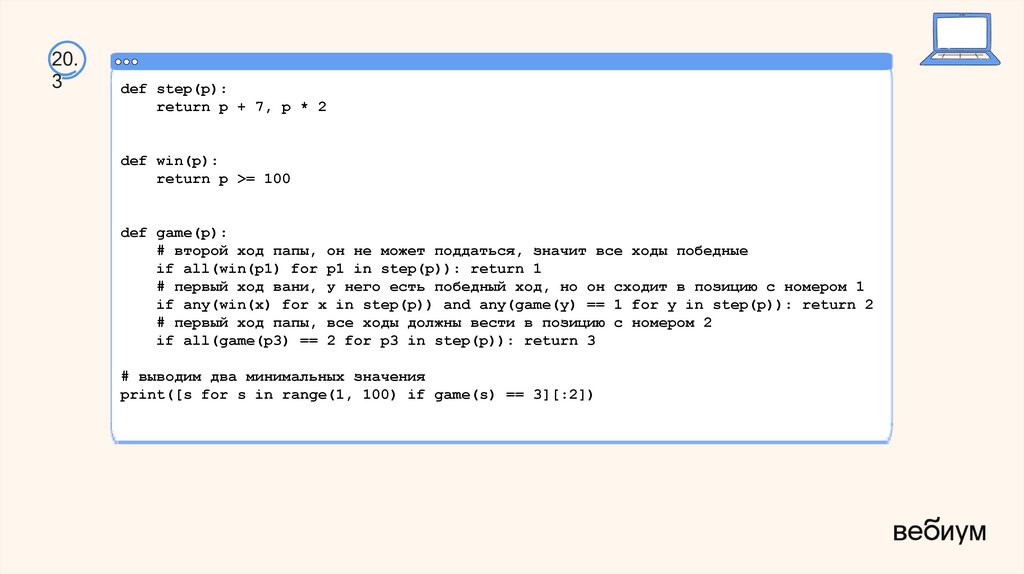
56.

20.
3
def step(p):
return p + 7, p * 2
def win(p):
return p >= 100
def game(p):
# второй ход папы, он не может поддаться, значит все ходы победные
if all(win(p1) for p1 in step(p)): return 1
# первый ход вани, у него есть победный ход, но он сходит в позицию с номером 1
if any(win(x) for x in step(p)) and any(game(y) == 1 for y in step(p)): return 2
# первый ход папы, все ходы должны вести в позицию с номером 2
if all(game(p3) == 2 for p3 in step(p)): return 3
# выводим два минимальных значения
print([s for s in range(1, 100) if game(s) == 3][:2])

57.

21.
3
Для игры, описанной в задании 19.3, найдите минимальное значение S, при котором
одновременно выполняются два условия:
– у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом
при любой игре Папы;
– у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
Если найдено несколько значений S, в ответе запишите минимальное из них.
пояснение
ответ
29

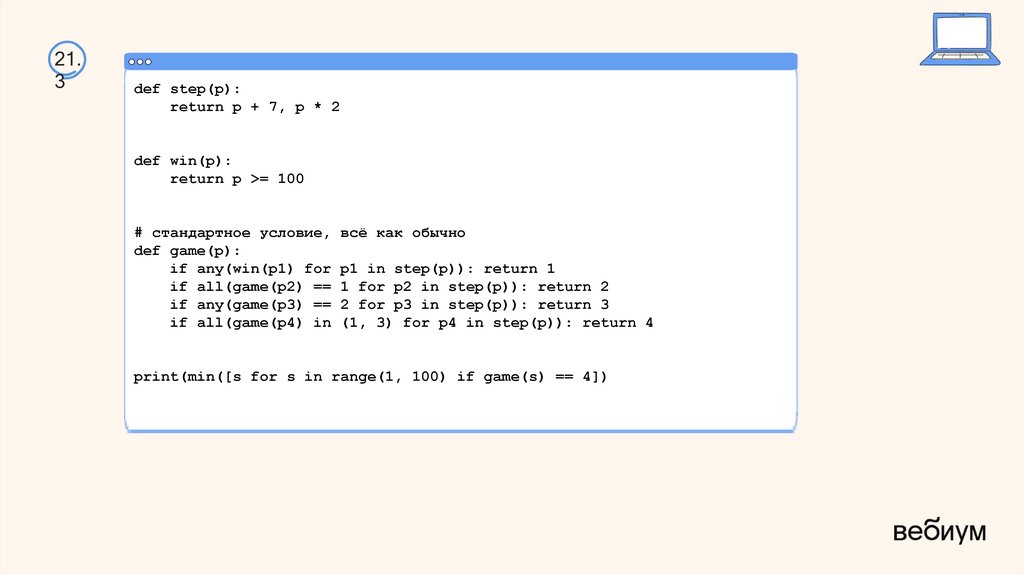
58.

21.
3
def step(p):
return p + 7, p * 2
def win(p):
return p >= 100
# стандартное условие, всё как обычно
def game(p):
if any(win(p1) for p1 in step(p)): return 1
if all(game(p2) == 1 for p2 in step(p)): return 2
if any(game(p3) == 2 for p3 in step(p)): return 3
if all(game(p4) in (1, 3) for p4 in step(p)): return 4
print(min([s for s in range(1, 100) if game(s) == 4])

59.

19.
4
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча, состоящая
из S конфет. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может
съесть не более половины от всех оставшихся конфет, но не менее одной конфеты.
Игра завершается в тот момент, когда в куче не остается ни одной конфеты. Победителем
считается игрок, который съел последнюю конфету.
Укажите максимальное двузначное значение S, при котором у Вани есть выигрышная
стратегия.
пояснение
95
ответ

60.

19.
4
Сначала распишем маленькие значения S:
при s = 1, Петя побеждает
при s = 2, Ваня побеждает
при s = 3, Петя побеждает
при s = 4, Петя может сходить в 2 или 3, из 2-ух он побеждает
при s = 5, Петя ходит в 3 или 4, из которых Ваня побеждает
при s = 6, Петя ходит в 3, 4 или 5, из 5 Петя побеждает
…
при s = 11, Петя может сходить только в те позиции, из которых Ваня победит
Если проанализировать все ходы, то можно увидеть закономерность:
Допустим Ваня победил в позиции x, тогда следующие x позиций будет побеждать Петя, а
следующая победная позиция для Вани будет x * 2 + 1.
С помощью проги, найдём максимальную двузначную позицию:
x = 2
while (x * 2 + 1) < 100:
x = x * 2 + 1
print(x)