Роль математики в формализации информационных процессов

1.

Роль математики в формализации
информационных процессов
Обеспечение строгости и
точности
Абстрагирование и
обобщение
Поддержка верификации
Устранение неоднозначностей и
Выявление общих структур в различных
Математическое доказательство
субъективных интерпретаций,
предметных областях, разработка
корректности программ, формальная
доказательное обоснование свойств
универсальных методов решения
проверка соответствия спецификации,
информационных систем, четкое
классов задач, построение иерархий
обнаружение логических ошибок и
определение границ применимости
абстракций различного уровня.
противоречий.
моделей и алгоритмов.
Основа для количественного анализа
Оценка сложности алгоритмов, анализ производительности информационных систем, оптимизация процессов обработки
информации.

2.

Историческая перспектива развития
математического аппарата
Античность и средние века
1
Аристотелева логика как первая система формальных рассуждений,
развитие алгебры и символического обозначения величин,
комбинаторные методы в работах средневековых математиков.
2
XVII-XIX века
Работы Лейбница по универсальному формальному языку, Булева
алгебра как основа формализации логических операций,
Первая половина XX века
3
формализация геометрии в работах Гильберта, развитие теории
множеств Кантором.
Формализация математики в работах Рассела и Уайтхеда, теория
вычислимости Тьюринга, Чёрча и Поста, логические основы
теории алгоритмов, создание теории информации Шенноном.
4
Вторая половина XX века – настоящее время
Теория формальных языков и грамматик Хомского, развитие
теории сложности вычислений, формальные методы верификации
программ, математические основы машинного обучения и
искусственного интеллекта.

3.

Теория множеств как основа формализации
Определение и значение
Теория множеств является одним из фундаментальных разделов
математики, обеспечивающих основу для формализации практически
любых математических понятий и структур. В информатике теория
множеств служит естественным языком для описания коллекций
объектов, их свойств и отношений.
Теория множеств предоставляет мощный инструментарий для
моделирования и анализа информационных структур, позволяя
формально описывать сложные отношения между объектами.

4.

Основные понятия теории множеств
Множество
Элемент множества
Совокупность объектов, рассматриваемая как единое
Объект, входящий в состав множества. Обозначается
целое. Ключевая особенность множества – его элементы
отношением принадлежности: x ∈ A (элемент x
уникальны и не упорядочены.
принадлежит множеству A).
Задание множеств
Основные множества
Перечислением элементов: A = {1, 2, 3, 4, 5}.
Пустое множество: ∅ или {}. Универсальное множество:
Характеристическим свойством: A = {x | P(x)}. С
U. Числовые множества: натуральные (ℕ), целые (ℤ),
помощью порождающей процедуры: A = {2n | n ∈ ℕ}.
рациональные (ℚ), действительные (ℝ).

5.

Операции над множествами
Объединение
Пересечение
Разность
A ∪ B = {x | x ∈ A или x ∈ B}
A ∩ B = {x | x ∈ A и x ∈ B}
A \ B = {x | x ∈ A и x ∉ B}
Множество всех элементов,
Множество всех элементов,
Множество всех элементов A, не
принадлежащих хотя бы одному из
принадлежащих одновременно
принадлежащих B.
множеств A или B.
множествам A и B.
Дополнение
Ā = {x | x ∈ U и x ∉ A}
Множество всех элементов универсального множества, не принадлежащих A.

6.

Свойства операций над множествами
Коммутативность
A ∪ B = B ∪ A, A ∩ B = B ∩ A
Ассоциативность
(A ∪ B) ∪ C = A ∪ (B ∪ C), (A ∩ B) ∩ C = A ∩ (B ∩ C)
Дистрибутивность
A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C), A ∪ (B ∩ C) = (A ∪
B) ∩ (A ∪ C)
Законы де Моргана
Ā ∪ B = Ā ∩ ̄B, Ā ∩ B = Ā ∪ ̄B
Идемпотентность
A ∪ A = A, A ∩ A = A
Свойства пустого множества
A ∪ ∅ = A, A ∩ ∅ = ∅
Свойства универсального множества
A ∪ U = U, A ∩ U = A

7.

Отношения между множествами
Равенство
Включение
(подмножество)
A = B, если каждый элемент A
является элементом B и наоборот.
Множества состоят из одних и тех
1
2
Несравнимость
Строгое включение
Множества не находятся в отношении
содержит элементы, не
принадлежащие другому множеству.
является элементом B. Все элементы
A содержатся в B.
же элементов.
включения. Каждое из множеств
A ⊆ B, если каждый элемент A
A ⊂ B, если A ⊆ B и A ≠ B. Все
4
3
элементы A содержатся в B, но B
содержит хотя бы один элемент, не
принадлежащий A.

8.

Декартово произведение и отношения
Декартово произведение
Бинарное отношение
Декартово произведение множеств A × B – множество всех
Бинарное отношение – подмножество декартова
упорядоченных пар (a, b), где a ∈ A и b ∈ B. Это
произведения R ⊆ A × B. Если A = B, то отношение
фундаментальная операция, позволяющая строить сложные
называется отношением на множестве A. Отношения
структуры из простых.
формализуют связи между элементами множеств.
Бинарные отношения могут обладать различными свойствами: рефлексивностью, симметричностью, транзитивностью,
антисимметричностью. Комбинации этих свойств определяют специальные типы отношений, такие как отношения
эквивалентности и порядка.

9.

Свойства бинарных отношений
Рефлексивность
∀a ∈ A: (a, a) ∈ R
Каждый элемент находится в отношении с самим собой.
Симметричность
Если (a, b) ∈ R, то (b, a) ∈ R
Если a находится в отношении с b, то и b находится в отношении с a.
Транзитивность
Если (a, b) ∈ R и (b, c) ∈ R, то (a, c) ∈ R
Если a находится в отношении с b, а b – с c, то a находится в отношении с c.
Антисимметричность
Если (a, b) ∈ R и (b, a) ∈ R, то a = b
Если a находится в отношении с b и b – с a, то a и b – один и тот же элемент.

10.

Специальные типы отношений
Отношение
эквивалентности
Отношение частичного
порядка
Отношение полного
порядка
Рефлексивное, симметричное,
Рефлексивное, антисимметричное,
Частичный порядок, в котором
транзитивное
транзитивное
любые два элемента сравнимы
Отношение эквивалентности разбивает множество на непересекающиеся классы эквивалентности. Отношения порядка
позволяют упорядочивать элементы множества, что критически важно для многих алгоритмов и структур данных.

11.

Применение теории множеств в
информатике
Моделирование структур данных
Массивы как отображения из множества индексов в
Формализация запросов к базам
данных
множество значений, множества как абстрактный тип
Реляционная алгебра основана на теории множеств,
данных (реализация через хеш-таблицы, деревья), графы
операции выборки, проекции, соединения как теоретико-
как пары множеств вершин и ребер.
множественные операции, оптимизация запросов с
использованием законов теории множеств.
Анализ алгоритмов
Логическое программирование
Определение входных и выходных данных как множеств,
Представление знаний через множества фактов и правил,
анализ корректности через теоретико-множественные
логический вывод как операции над множествами,
отношения, исследование сложности через мощность
унификация как поиск общих элементов множеств.
множеств.

12.

Логические исчисления
Логические исчисления предоставляют формальные системы для моделирования рассуждений и вывода. Они являются
основой для представления знаний, автоматизации доказательств и построения логических выводов в информационных
системах.
Исчисление
высказываний
Исчисление предикатов
Нечеткая логика
Формальная система, оперирующая с
Расширяет исчисление высказываний,
логику, позволяя моделировать
высказываниями, которые могут быть
добавляя понятия предикатов,
неопределенность и частичную
либо истинными, либо ложными.
переменных, кванторов и функций.
истинность утверждений.
Расширяет классическую булеву

13.

Исчисление высказываний
Основные понятия
Таблицы истинности
Атомарные высказывания: обозначаются символами p,
Метод определения истинностного значения сложных
q, r, ...
формул через значения их компонентов. Для каждой
Логические связки: отрицание (¬), конъюнкция (∧),
комбинации значений атомарных высказываний вычисляется
дизъюнкция (∨), импликация (→), эквивалентность (↔)
значение всей формулы.
Таблицы истинности позволяют определить, является ли
Формулы: выражения, построенные из атомарных
формула тавтологией (истинна при любых значениях
высказываний с помощью логических связок
переменных) или противоречием (всегда ложна).

14.

Логическая эквивалентность и
тавтологии
Логически
эквивалентные
формулы
Тавтология
Противоречие
Формула, истинная при любых
Формула, ложная при любых
значениях входящих в неё
значениях входящих в неё
A ≡ B, если формулы имеют
переменных. Тавтологии
переменных. Противоречия
одинаковые таблицы истинности.
представляют логические законы,
представляют логически
Эквивалентные формулы могут
которые всегда верны.
невозможные ситуации.
заменять друг друга в любом
контексте.
Понимание логической эквивалентности и тавтологий критически важно для упрощения логических выражений, оптимизации
схем и доказательства теорем.

15.

Основные эквивалентности в исчислении
высказываний
Идемпотентность
p ∧ p ≡ p, p ∨ p ≡ p
Коммутативность
p ∧ q ≡ q ∧ p, p ∨ q ≡ q ∨ p
Ассоциативность
(p ∧ q) ∧ r ≡ p ∧ (q ∧ r), (p ∨ q) ∨ r ≡ p ∨ (q ∨ r)
Дистрибутивность
p ∧ (q ∨ r) ≡ (p ∧ q) ∨ (p ∧ r), p ∨ (q ∧ r) ≡ (p ∨ q)
∧ (p ∨ r)
Законы де Моргана
¬(p ∧ q) ≡ ¬p ∨ ¬q, ¬(p ∨ q) ≡ ¬p ∧ ¬q
Определение импликации
p → q ≡ ¬p ∨ q
Двойное отрицание
¬¬p ≡ p

16.

Исчисление предикатов первого
порядка
Основные понятия
Синтаксис исчисления предикатов
Предикаты: функции, возвращающие истинностные
значения (например, P(x) означает "x обладает
свойством P")
выражения
Переменные: представляют объекты из некоторой
предметной области
Кванторы: всеобщности (∀) и существования (∃)
Функциональные символы: обозначают отображения
объектов
Термы: переменные, константы, функциональные
Атомарные формулы: предикаты, применённые к
термам
Сложные формулы: построенные из атомарных с
помощью логических связок и кванторов

17.

Примеры формул исчисления предикатов
∀x(Human(x) → Mortal(x)) – "Все люди смертны"
∃x(Student(x) ∧ Programming(x)) – "Существует студент, изучающий программирование"
∀x∀y(Parent(x, y) → Older(x, y)) – "Любой родитель старше своего ребёнка"

18.

Интерпретация и модели в исчислении
предикатов
Интерпретация
Модель формулы
Модель формулы –
Общезначимая
формула
(тавтология)
Выполнимая
формула
Выполнимая формула истинна
хотя бы при одной
Интерпретация задает область
интерпретация, при которой
Общезначимая формула
интерпретации. Выполнимость
определения переменных и
формула истинна. Формула
истинна при любой
означает, что существует хотя
значения предикатных и
может иметь множество
интерпретации. Такие
бы один "мир", в котором
функциональных символов.
различных моделей или не
формулы выражают
формула верна.
Она определяет конкретный
иметь их вовсе.
универсальные логические
"мир", в котором
законы, не зависящие от
оцениваются формулы.
конкретной предметной
области.

19.

Нечеткая логика
Основные понятия
Нечеткая логика (fuzzy logic) расширяет классическую булеву логику, позволяя
моделировать неопределенность и частичную истинность утверждений. В нечеткой логике
истинностные значения могут принимать любые значения из интервала [0, 1], а не только
0 (ложь) и 1 (истина).
Нечеткое множество: обобщение классического множества, в котором степень
принадлежности элемента может быть любым числом от 0 до 1
Функция принадлежности: отображение, определяющее степень принадлежности
элемента нечеткому множеству

20.

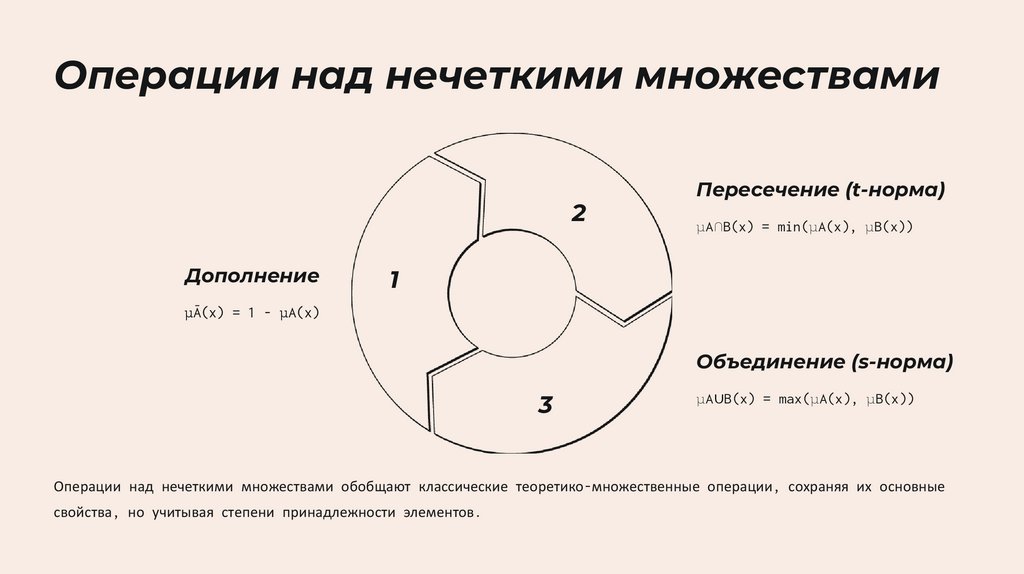
Операции над нечеткими множествами
2
Дополнение
Пересечение (t-норма)
μA∩B(x) = min(μA(x), μB(x))
1
μĀ(x) = 1 - μA(x)
Объединение (s-норма)
3
μA∪B(x) = max(μA(x), μB(x))
Операции над нечеткими множествами обобщают классические теоретико-множественные операции, сохраняя их основные
свойства, но учитывая степени принадлежности элементов.

21.

Применение нечеткой логики
Системы нечеткого
управления
Обработка
естественного языка
Экспертные системы
Используются в автоматизированных
Применяется для формализации
оперирующие с неточными знаниями
системах управления, где требуется
нечетких лингвистических понятий и
и выводами, что особенно важно в
моделирование экспертных знаний и
правил, что позволяет создавать
таких областях как медицинская
работа с неточными данными.
более гибкие системы понимания и
диагностика, финансовый анализ и
Примеры: управление бытовой
генерации текста, машинного
управление рисками.
техникой, промышленными
перевода и информационного
процессами, транспортными
поиска.
средствами.
Позволяет создавать системы,

22.

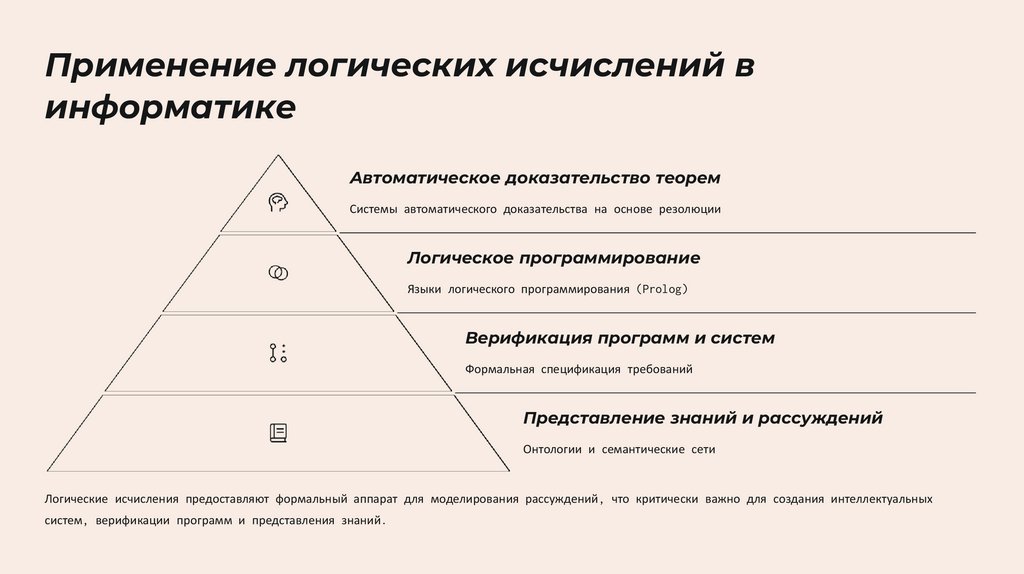
Применение логических исчислений в
информатике
Автоматическое доказательство теорем
Системы автоматического доказательства на основе резолюции
Логическое программирование
Языки логического программирования (Prolog)
Верификация программ и систем
Формальная спецификация требований
Представление знаний и рассуждений
Онтологии и семантические сети
Логические исчисления предоставляют формальный аппарат для моделирования рассуждений, что критически важно для создания интеллектуальных
систем, верификации программ и представления знаний.

23.

Формальные языки и грамматики
Формальные языки и грамматики предоставляют математический аппарат для описания синтаксиса языков, включая языки программирования, и лежат в основе теории компиляции и автоматического анализа текстов.
Основные понятия
Алфавит (Σ) – конечное непустое множество символов
Цепочка (слово) – конечная последовательность символов из алфавита
Язык – множество цепочек над заданным алфавитом

24.

Операции над языками
Объединение
Конкатенация
L₁ ∪ L₂ = {w | w ∈ L₁ или w ∈ L₂}
L₁ · L₂ = {w₁w₂ | w₁ ∈ L₁, w₂ ∈
Итерация (замыкание
Клини)
L₂}
L* = {ε} ∪ L ∪ L² ∪ L³ ∪ ...
Множество всех цепочек,
Множество всех цепочек,
Множество всех цепочек,
принадлежащих хотя бы одному из
полученных приписыванием цепочки
полученных конкатенацией любого
языков.
из L₂ к цепочке из L₁.
числа (включая ноль) цепочек из
L.
Положительное замыкание
L⁺ = L · L*
Множество всех цепочек, полученных конкатенацией одной или более цепочек из L.

25.

Формальные грамматики
Определение
Вывод в грамматике
Формальная грамматика – это математическая система,
Вывод в грамматике – последовательность применений
задающая язык через правила порождения цепочек.
правил, начиная с начального символа S. Цепочка w
Формально, грамматика G задается четверкой (V, Σ, P,
принадлежит языку L(G), если существует вывод S ⇒* w.
S), где:
V – алфавит нетерминальных символов
Пример грамматики для языка правильных скобочных
Σ – алфавит терминальных символов (V ∩ Σ = ∅)
выражений:
P – конечное множество правил вывода вида α → β,
V = {S}
где α, β ∈ (V ∪ Σ)*
Σ = {(, )}
P = {S → ε, S → (S), S → SS}
Начальный символ: S
S – начальный символ (S ∈ V)

26.

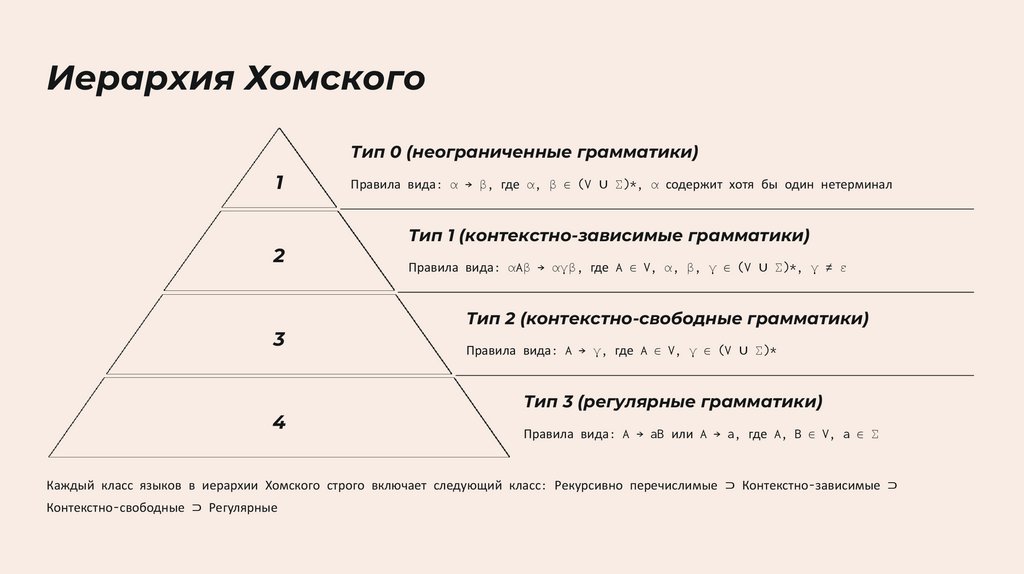
Иерархия Хомского
Тип 0 (неограниченные грамматики)
1
2
3
4
Правила вида: α → β, где α, β ∈ (V ∪ Σ)*, α содержит хотя бы один нетерминал
Тип 1 (контекстно-зависимые грамматики)
Правила вида: αAβ → αγβ, где A ∈ V, α, β, γ ∈ (V ∪ Σ)*, γ ≠ ε
Тип 2 (контекстно-свободные грамматики)
Правила вида: A → γ, где A ∈ V, γ ∈ (V ∪ Σ)*
Тип 3 (регулярные грамматики)
Правила вида: A → aB или A → a, где A, B ∈ V, a ∈ Σ
Каждый класс языков в иерархии Хомского строго включает следующий класс: Рекурсивно перечислимые ⊃ Контекстно-зависимые ⊃
Контекстно-свободные ⊃ Регулярные

27.

Конечные автоматы
Определение
Конечный автомат (КА) – математическая модель,
описывающая устройство с конечным числом состояний,
которое может находиться в одном из этих состояний в
любой момент времени. КА переходит из одного состояния в
другое в ответ на внешние входные сигналы.
Формально, детерминированный конечный автомат (ДКА)
задается пятеркой (Q, Σ, δ, q₀, F), где:
Q – конечное множество состояний
Σ – входной алфавит
δ: Q × Σ → Q – функция переходов
q₀ ∈ Q – начальное состояние
F ⊆ Q – множество допускающих состояний
Конечные автоматы широко используются для моделирования
систем с конечным числом состояний, распознавания
регулярных языков и проектирования цифровых схем.

28.

Недетерминированные конечные
автоматы
Определение
Теорема о детерминизации
Недетерминированный конечный автомат (НКА) –
Для любого НКА существует эквивалентный ДКА,
обобщение ДКА, в котором:
распознающий тот же язык. Это означает, что НКА и ДКА
Функция переходов имеет вид δ: Q × (Σ ∪ {ε}) → 2^Q
Из одного состояния по одному символу возможны
переходы в несколько состояний
Возможны ε-переходы (переходы без чтения входного
символа)
имеют одинаковую выразительную мощность – оба класса
автоматов распознают в точности регулярные языки.
Процесс преобразования НКА в ДКА называется
детерминизацией и основан на построении состояний ДКА
как подмножеств состояний НКА.

29.

Применение конечных автоматов
Лексический анализ в
компиляторах
Распознавание
регулярных выражений
Моделирование
протоколов связи
Конечные автоматы используются для
Регулярные выражения, широко
Конечные автоматы позволяют
распознавания лексем (токенов) в
используемые в обработке текстов и
моделировать состояния и переходы в
исходном коде программы. Каждый
поиске, реализуются через конечные
протоколах связи, что упрощает их
тип лексемы (идентификатор, число,
автоматы. Каждое регулярное
анализ, верификацию и реализацию.
ключевое слово) описывается своим
выражение может быть преобразовано
регулярным выражением и
в эквивалентный конечный автомат.
распознается соответствующим
автоматом.
Проектирование последовательностных схем
Цифровые схемы с памятью (триггеры, регистры, счетчики) проектируются на основе моделей конечных автоматов, что
обеспечивает их корректную работу во всех возможных состояниях.

30.

Контекстно-свободные грамматики и
синтаксический анализ
Деревья вывода
Форма Бэкуса-Наура (BNF)
Деревья вывода (синтаксические деревья) – графическое
Распространенная нотация для записи КСГ:
представление деривации цепочки в КСГ. Внутренние узлы
дерева помечены нетерминалами, листья – терминалами
<expr> ::= <expr> "+" <term> | <term>
или ε.
<term> ::= <term> "*" <factor> | <factor>
Синтаксические деревья наглядно показывают структуру
предложения языка и используются в компиляторах для
<factor> ::= "(" <expr> ")" | <identifier>
<identifier> ::= "a" | "b" | ... | "z"
построения абстрактного синтаксического дерева.
BNF широко используется для описания синтаксиса языков
программирования и протоколов.

31.

Методы синтаксического анализа для
КСГ
Нисходящий анализ
Восходящий анализ
Универсальные методы
LL-анализаторы, рекурсивный спуск.
LR-анализаторы, операторная
Алгоритм Кока-Янгера-Касами,
Начинает с начального символа и
грамматика. Начинает с входной
алгоритм Эрли. Работают с любыми
пытается построить дерево вывода
строки и пытается свести её к
КСГ, но имеют более высокую
сверху вниз.
начальному символу.
вычислительную сложность.
Выбор метода синтаксического анализа зависит от свойств грамматики, требований к эффективности и простоте реализации.
В современных компиляторах чаще всего используются LR-анализаторы из-за их эффективности и широкого охвата грамматик.

32.

Применение формальных языков и
грамматик в информатике
Компиляторы и
интерпретаторы
Инструменты
разработки (IDE)
Системы обработки
документов
Формальные грамматики
Интегрированные среды разработки
XML, HTML и другие языки разметки
используются для описания
используют формальные грамматики
описываются с помощью
синтаксиса языков
для подсветки синтаксиса,
формальных грамматик, что
программирования, что позволяет
автодополнения кода, рефакторинга
обеспечивает их стандартизацию и
автоматизировать создание
и других функций, повышающих
создание эффективных парсеров для
компиляторов и интерпретаторов с
продуктивность программистов.
обработки документов.
помощью генераторов
синтаксических анализаторов.