Основы воздушной навигации введение

1. Основы воздушной навигации введение

Воздушная навигация – наука о точном,
надежном и безопасном вождении воздушных
судов из одной точки земной поверхности в
другую.
Самолетовождение - комплекс действий
экипажа самолета и работников службы
движения, направленных на обеспечение
безопасности, наибольшей точности выполнения
полетов по установленным трассам (маршрутам)
и прибытия в пункт назначения в заданное
время.

2. Формы и размеры Земли

Уровенная поверхность – поверхность, во
всех точках перпендикулярная направлению силы
тяжести (отвесной линии).
В качестве сглаженной фигуры Земли разумно
выбрать форму уровенной поверхности,
совпадающей с физической поверхностью в морях и
океанах, где нет неровностей рельефа. Такая фигура
получила название геоида.
Геоид – фигура, образованная уровенной
поверхностью, совпадающей в морях и океанах с их
средней поверхностью.

3.

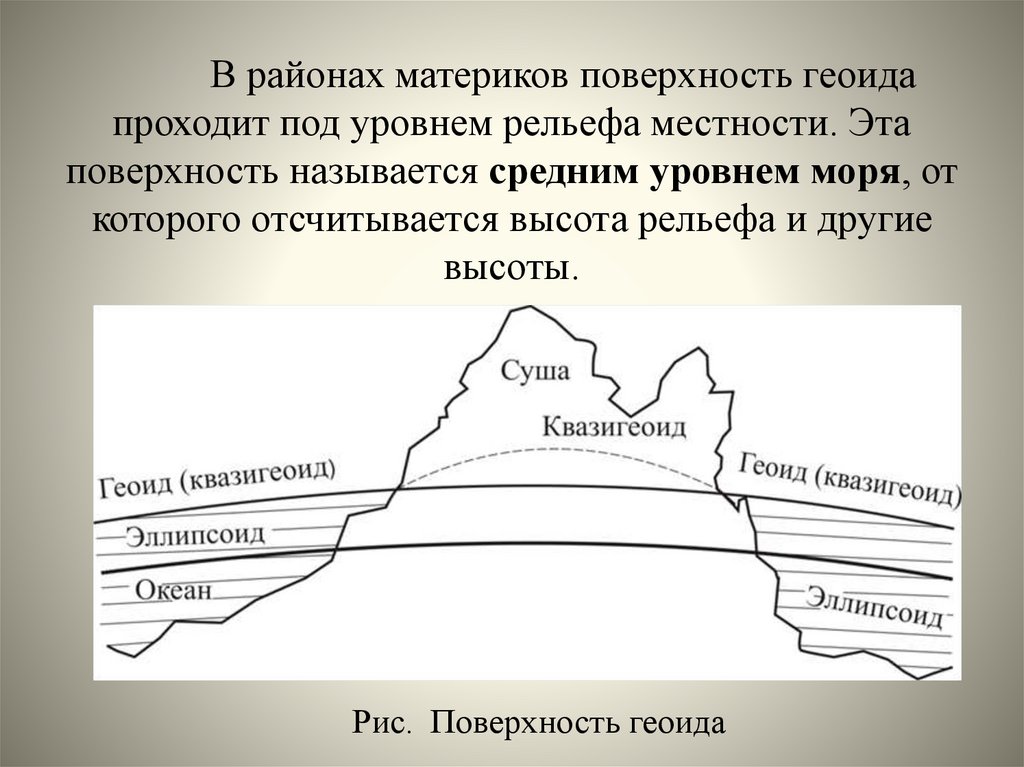
В районах материков поверхность геоида
проходит под уровнем рельефа местности. Эта
поверхность называется средним уровнем моря, от
которого отсчитывается высота рельефа и другие
высоты.
Рис. Поверхность геоида

4.

В России за начало уровня отсчета высот принято
нулевое деление футштока (мерной линейки),
установленной в Обводном канале г. Кронштадта.
Для удобства навигационных расчетов форму Земли
представляют в виде шара с незначительным сжатием у
полюсов. Этот эллипс имеет следующие размеры:
экваториальный радиус а = 6378 км, полярный радиус b =
6357 км
В воздушной навигации в
большинстве случаях сжатием
Земли пренебрегают и принимают
Землю условно за шар, радиус
которого составляет 6371 км.
Земной элипсоид

5.

Если очень высокая точность решения
навигационных задач не требуется, то Землю можно
рассматривать как сферу.
В этом случае используется нормальная
сферическая система координат, полюсы которой
совпадают с географическими полюсами нашей
планеты, т. е. точками, в которых оси вращения
Земли пересекает ее поверхность. Система
координат на сфере строится с помощью больших
кругов.

6.

Сферические координаты
Большим кругом называется
окружность, образующаяся в
результате сечения сферы
плоскостью, проходящей через
центр Земли.
Экватором называется большой
круг, плоскость которого
перпендикулярна оси вращения
Земли
Меридианом истинным, или
географическим, называется
большой круг, плоскость
которого проходит через ось
вращения Земли.
На земном шаре можно провести бесчисленное количество
меридианов. Все меридианы сходятся у географических полюсов
земли и расходятся к экватору

7.

Начальным меридианом, или нулевым, является
Гринвичский меридиан,
который когда-то проходил через расположенную
вблизи г. Лондона Гринвичскую обсерваторию
(сейчас обсерватория находится в другом месте, но
меридиан сохранился). В XIX в. в разное время в
качестве начального использовались и другие
меридианы (Парижа, острова Ферро в
Атлантическом океане, Пулковской обсерватории
под Петербургом).

8.

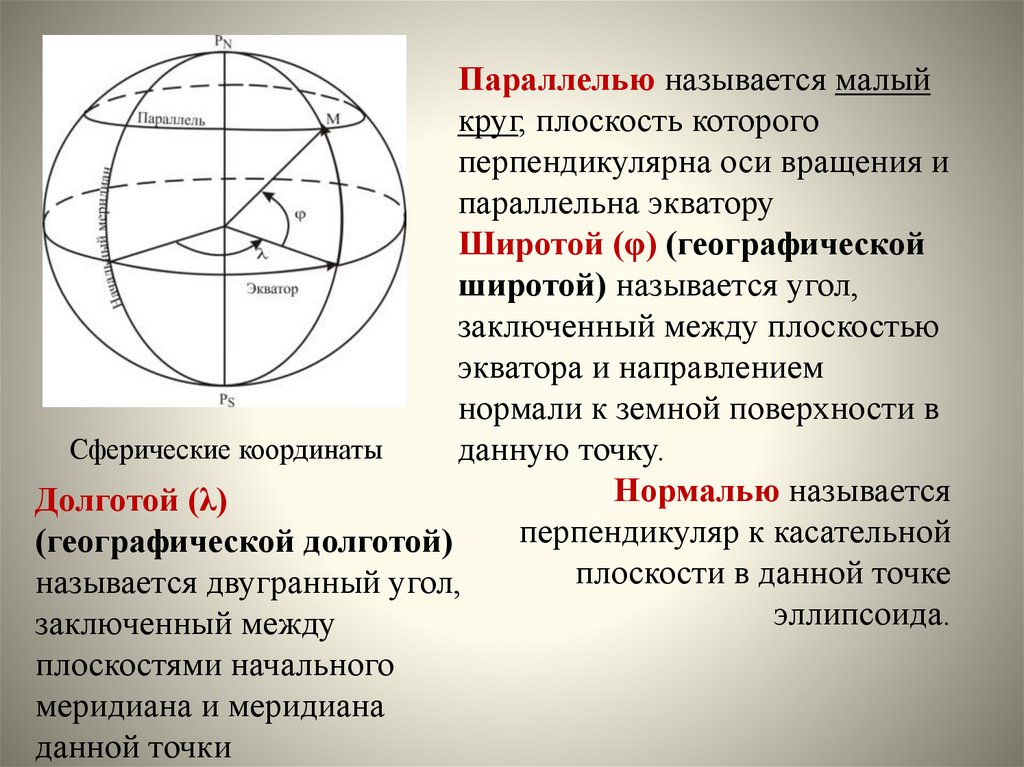
Параллелью называется малый
круг, плоскость которого
перпендикулярна оси вращения и
параллельна экватору
Широтой (φ) (географической
широтой) называется угол,
заключенный между плоскостью
экватора и направлением
нормали к земной поверхности в
Сферические координаты
данную точку.
Нормалью называется
Долготой (λ)
перпендикуляр к касательной
(географической долготой)
плоскости в данной точке
называется двугранный угол,
эллипсоида.
заключенный между
плоскостями начального
меридиана и меридиана
данной точки

9.

• Широта отсчитывается от плоскости экватора к
полюсам от 0 до 90° к северу или югу.
• Долгота отсчитывается в обе стороны от начального
меридиана от 0 до 180 . Если данная точка
расположена в восточном полушарии, то долгота
считается восточной, если в западном полушарии –
западной.

10.

• При расчетах по формулам западной и восточной
долготе можно приписывать знаки соответственно «–»
и «+» (или наоборот, как это принято, например, в
США).
• Единицами измерения широты и долготы являются
угловые градусы, минуты и секунды, а иногда и их
десятичные доли (десятые, сотые и т. д.).
• За рубежом используются следующие буквенные
обозначения: N (North) – север; S (South) – юг;
Е (East) – восток; W (West) – запад.
Одни и те же значения широты и долготы в
документах аэронавигационной информации при
выполнении различных навигационных расчетов могут
быть представлены по-разному, например:
47° 23' 12" с.ш. = N47° 23.2' = +47.38667°.
124° 45' 45" з.д. = W124° 45.75' = –124.7625°.

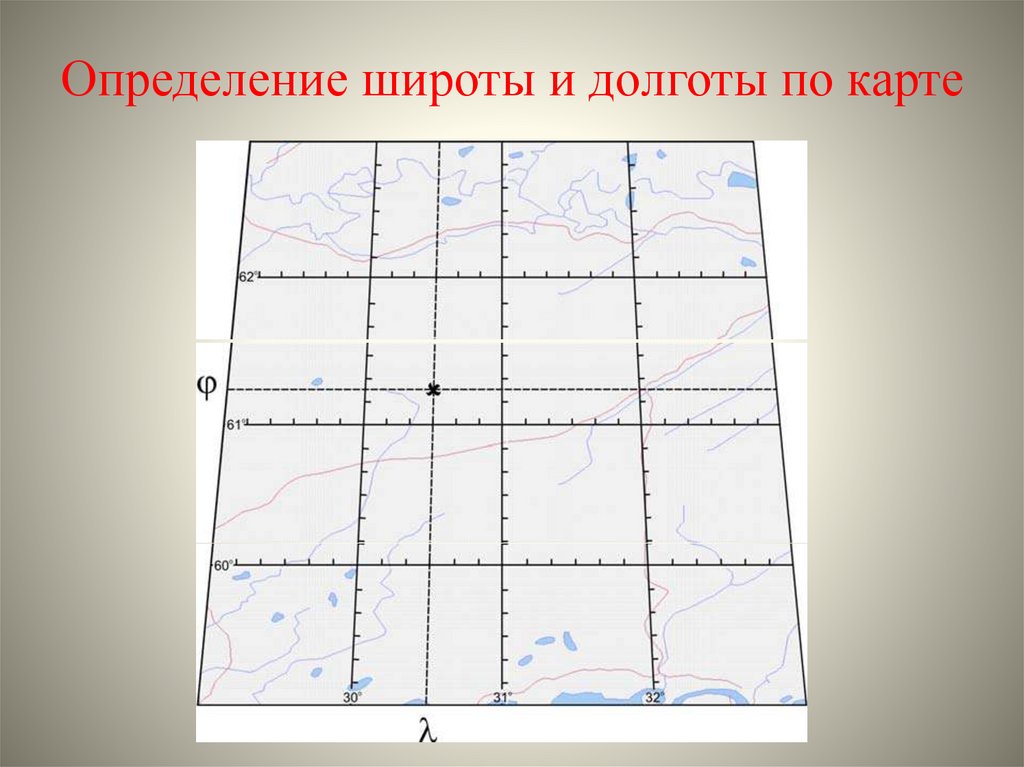
11. Определение широты и долготы по карте

12.

13.

Сферическая система координат не обязательно должна быть
нормальной, географические полюсы Земли и полюсы системы
координат могут не совпадать.
Если представить сетку меридианов и параллелей в виде сетки,
надетой на глобус (Землю), то ее можно сместить по поверхности
сферы и разместить полюсы системы координат (точки схождения
меридианов) в любом месте. В таких смещенных системах
координат также будут свои широты и долготы, но измеряться они
будут с помощью условных меридианов и параллелей.
В картографии такие системы координат
называют косыми сферическими,
а в навигации – ортодромическими
системами координат (рис.).
Рис. Косая сферическая система координат

14.

• Угол схождения меридианов на сфере
Угол схождения меридианов имеет очень важное
значение в навигации.
Он используется при расчете и прокладке линий
положения, при преобразовании направлений (курсов,
путевых углов, пеленгов) из одной системы отсчета в
другую. Он является составной частью азимутальной
поправки, используемой при переходе от истинного
меридиана к опорному.

15.

Угол схождения меридианов в двух точках сферы
(δсх) – это разность путевых углов ортодромии,
проходящей через эти точки (рис. 2.3).
• Ортодромия пересекает
меридианы под различными
углами. Если в первой точке
с координатами φ1, λ1 путевой
угол β1 , а во второй точке с
координатами φ2 , λ2 путевой
угол β2 , то по определению:
Рис. 2.3. Угол схождения меридианов
Если прямой β1 и обратный βобр путевые углы уже известны, то
найти β2 достаточно просто:

16.

• Можно использовать для нахождения β2 и основное
свойство ортодромии, в соответствии с которым
Откуда
Но для решения многих навигационных задач сами путевые углы
не нужны, а интересует только угол схождения меридианов.
Если известны только координаты обеих точек, то значение
угла схождения меридианов на сфере может быть рассчитано по
следующей точной формуле :
Эта точная, хотя и
несколько громоздкая,
формула может быть
использована при любом
расстоянии между точками.

17.

• При сравнительно небольших расстояниях ее можно
упростить. Если разности широт и долгот точек невелики, то
углы δсх и (λ2 – λ1) малы и их тангенсы можно заменить
значениями самих углов (в радианах), а косинус
полуразности широт можно принять равным единице. Тогда
легко получить:
где φср – средняя
широта
данных двух точек.
Несмотря на то, что эта формула является приближенной, она
дает вполне точные для практики результаты на довольно
больших расстояниях и поэтому широко применяется в
навигации. Для примера приведем результаты расчета δсх для
трех ортодромий по приближенной и точной формулам с
точностью до минуты. Санкт-Петербург-Москва: точно 6°11', приближенно 6°11'.
Санкт-Петербург-Новосибирск: точно 45°16', приближенно 44°20'.
Санкт-Петербург-Владивосток: точно 88°15', приближенно 79°32'.

18.

• Таким образом, даже на расстояниях, измеряемых двумятремя тысячами километров (Новосибирск), погрешность не
превышает 1°. Если же речь идет о сотнях километров
(в средних широтах), то приближенная формула практически
точна. В полярных районах, где меридианы расположены
«густо», даже при небольшом расстоянии между точками
разность их долгот и, следовательно, угол схождения
меридианов, могут быть велики.
Угол схождения меридианов имеет знак.
В северном полушарии (когда широты положительны), если
вторая точка находится восточнее первой, δсх положителен,
а если западнее – отрицателен.
В южном полушарии – наоборот.

19. Системы координат, применяемые в воздушной навигации

При работе с наземными и техническими
средствами самолетовождения приходится
использовать различные системы координат,
основными из которых являются
географическая, ортодромическая,
прямоугольная, полярная системы
координат.

20.

• Географические системы координат уже рассмотрены
выше. Достоинством таких систем является то, что они
являются едиными для всей Земли: координаты точки
однозначно определяют ее местоположение. Но они неудобны
для определения местоположения ВС относительно заданной
траектории. Например, зная широту и долготу, невозможно
сразу сказать, находится ВС на ЛЗП или уклонилось от нее.
• Ортодромические системы координат являются
обобщающим случаем сферических координат. Вместо
«настоящих» меридианов и параллелей, как в
географических системах, используются меридианы и
параллели условные, наиболее удобно расположенные
относительно маршрута полета.
В ортодромических системах осями являются две
ортодромии, перпендикулярные друг другу в начале системы
координат. В зависимости от того, как направлены эти оси и где
расположено начало системы координат, различают две их группы:
главноортодромическая и частноортодромическая.

21.

• Прямоугольные системы координат
Прямоугольные системы координат − это обычные
декартовы системы, имеющие три перпендикулярных оси
(X, Y, Z). Они используются для описания положения точек в
пространстве, на поверхности или внутри Земли.
Если начало прямоугольной
системы координат (точка
пересечения трех осей)
расположено в центре масс
Земли, то систему называют
геоцентрической, а если в
центре аппроксимирующего
Землю эллипсоида - референцной.
Геоцентрическая и топоцентрическая
системы координат

22.

Системы координат, начало которых находится на
поверхности Земли, называют топоцентрическими
(рис. выше). Топоцентрические системы
используются для определения положения точек на
небольшой территории, в пределах которой
кривизной Земли можно пренебречь.
(Например, координаты препятствий в районе
аэродрома предоставляются в топоцентрической
системе, начало которой расположено в точке
пересечения осевой линии и порога ВПП.)
В геоцентрических системах координат ось OZ
направлена по оси вращения Земли, а в
референцных – по малой оси эллипсоида в
сторону Северного полюса. Оси ОХ и ОY лежат в
плоскости экватора перпендикулярно друг другу.

23.

В зависимости от того, вращается ли система координат
вместе с Землей, различают гринвичские и инерциальные
системы (рис. 1.5).
В гринвичской системе координат
ось ОХГ лежит в плоскости
Гринвичского меридиана и
пересекает поверхность Земли в
точке с широтой и долготой
равными нулю. Такая система
координат вращается вместе с
Землей, поэтому координаты
точек на Земле в течение суток
не меняются.
Рис. 1.5. Гринвичская и инерциальная
системы координат

24.

• В инерциальной системе координат ось ОХИ направлена в
точку весеннего равноденствия
на небесной сфере. Это точка, в
которой пересекаются
небесный экватор и эклиптика.
Можно считать, что она
занимает фиксированное
положение относительно звезд.
Поскольку эта система координат фиксирована относительно
небесной сферы и вместе с Землей не вращается, координаты
точек на вращающейся Земле непрерывно изменяются. Вместе
с тем взаимное расположение инерциальной и гринвичской
систем может быть точно определено в любой момент
времени, поскольку угол между осями OXГ и ОХИ – это
гринвичское звездное время (Sгр).

25.

Прямоугольные геоцентрические и референцные
системы координат используются в спутниковых
навигационных системах, которые основаны на
измерении расстояния от самолета до спутников.
Спутники движутся по законам небесной механики в
соответствии с уравнениями, описываемыми в
инерциальной системе координат.
После определения пространственного места
самолета в этой системе его координаты
пересчитываются в гринвичскую прямоугольную, а
затем в геодезическую систему координат.

26.

Системы координат, начало которых находится на
поверхности Земли, называют топоцентрическими
(рис. выше). Топоцентрические системы
используются для определения положения точек на
небольшой территории, в пределах которой
кривизной Земли можно пренебречь.
(Например, координаты препятствий в районе
аэродрома предоставляются в топоцентрической
системе, начало которой расположено в точке
пересечения осевой линии и порога ВПП.)
В геоцентрических системах координат ось OZ
направлена по оси вращения Земли, а в
референцных – по малой оси эллипсоида в
сторону Северного полюса. Оси ОХ и ОY лежат в
плоскости экватора перпендикулярно друг другу.

27.

• В полярной системе координат определяются полярные
координаты объекта (самолета, радиостанции, ориентира
и т. д.) относительно какой-либо заранее оговоренной или
подразумеваемой точки (как бы полюса этой системы
координат). Этой точкой обычно бывает радиомаяк или
самолет.
Нельзя говорить о полярных координатах радиомаяка
относительно самого радиомаяка или о координатах
самолета относительно самого себя. Поэтому, когда говорят
о полярных координатах ВС, начало координат
подразумевается в другой точке (обычно, радиомаяке), и
наоборот, полярные координаты радиомаяка могут быть
указаны относительно самолета.

28.

• Координатами в полярной системе являются пеленг и
дальность.
Дальность (D) – расстояние от начала системы
координат до объекта (точки).
Различают наклонную дальность, измеренную по прямой
от радиомаяка до рассматриваемой точки (например, до
МПС) и
горизонтальную, от радиомаяка до точки на земной
поверхности под самолетом, то есть до МС.
• Наклонная дальность всегда больше горизонтальной, а
совпадает с ней, когда рассматриваемая точка (например,
самолет) находится на поверхности земли. Наклонная
дальность непосредственно измеряется
радионавигационными системами. Горизонтальная
дальность используется для определения МС на карте.

29.

• Пеленг – угол в горизонтальной плоскости между
направлением, принятым за начало отсчета и направлением на
объект. Пеленг отсчитывается по часовой стрелке и
измеряется от 0 до 360°.
Если объект находится к северу, его пеленг составляет 0°,
если к востоку – 90°, к югу – 180°, а к западу – 270°.
Часто вместо специфического навигационного термина «пеленг»
используется общепринятое (например, в географии) слово
«азимут».